Algorithms #13
Dynamic programming

Those who cannot remember the past are condemned to repeat it.
George Santayana
Dynamic programming
Dynamic Programming
What is it actually ?

The word dynamic was chosen by Bellman to capture the time-varying aspect of the problems, and because it sounded impressive.

Richard Ernest Bellman
American applied mathematician, who introduced dynamic programming in 1953, and made important contributions in other fields of mathematics.
The core idea of Dynamic Programming is to avoid repeated work by remembering partial results and this concept finds it application in a lot of real life situations
1+1+1+1+1+1+1+1 =
What's that equal to?
8
1+
9
How'd you know it was nine so fast?
You just added one more
So you didn't need to recount because you remembered there were eight! Dynamic Programming is just a fancy way to say 'remembering stuff to save time later
In programming, Dynamic Programming is a powerful technique that allows one to solve different types of problems in time O(n^2) or O(n^3) for which a naive approach would take exponential time.
Dynamic Programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems, solving each of those subproblems just once, and storing their solutions using a memory-based data structure (array, map,etc).


Overlapping sub-problems
The two required properties of dynamic programming are
- Optimal substructure: optimal solution of the sub-problem can be used to solve the overall problem.
- Overlapping sub-problems: sub-problems recur many times. Solutions of sub-problems can be cached and reused
Let's try to understand this by taking an example of Fibonacci numbers.
/**
Fibonacci (n) = 1; if n = 0
Fibonacci (n) = 1; if n = 1
Fibonacci (n) = Fibonacci(n-1) + Fibonacci(n-2)
*/
function fib(n) {
// implement this
}Try to find 30th, 31th fib number
What is the complexity ?
How we can improve things ?
/**
Fibonacci (n) = 1; if n = 0
Fibonacci (n) = 1; if n = 1
Fibonacci (n) = Fibonacci(n-1) + Fibonacci(n-2)
*/
function fib(n, cache) {
// implement this
}Rewrite a function to use cache
You can't solve all algorithmic problems with a dynamic programming
What kind of problems can be solved using dynamic programming ?

Optimization problems
Combinatorial problems
finding the best solution from all feasible solutions
Where can be many solutions. And we wish to find the optimal value
finding an optimal object from a finite set of objects
figure out the number of ways to do something, or the probability of some event happening
Real life applications of dynamic programming?
- In Google Maps to find the shortest path
- in the field of Biology to find the matching trends between two genes
- git merge
- In large warehouses, box packing with minimal cost
- LaTeX
- artificial intelligence, automatic speech recognition
- Time-sharing: It schedules the job to maximize CPU usage
- Optimal Control, for starters, which is applicable in aerospace systems, chemical control systems, robotics, and much more
- Other optimization problems
Lets start with simple problems

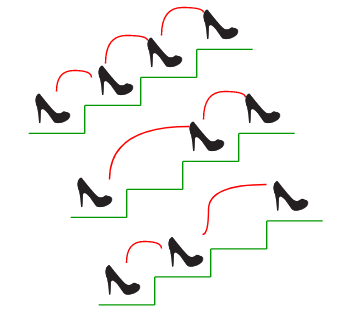
Stairs problem
You can climb 1 or 2 stairs with one sep. How many different ways can you climb n stairs ?
function stairs(n, /* cache ? */) {
// implement this
}
General steps of solving DP
1. Solve base cases
2. Define what is n-th value means
3. Get the recurent formula
4. Define base cases and constraints
5. Define the order of calculation
6. Find out the result
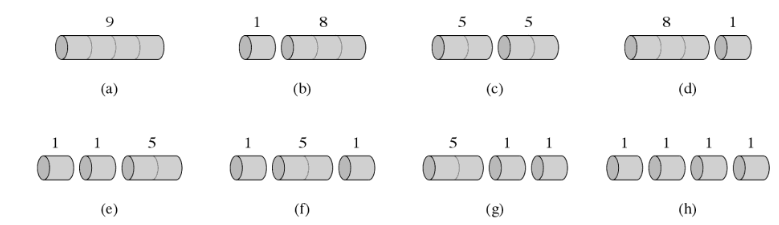
Rods problem
You are given a rod of size n >0, it can be cut into any number of pieces k (k ≤ n). Price for each piece of size i is represented as p(i) and maximum revenue from a rod of size i is r(i) (could be split into multiple pieces). Find r(n) for the rod of size n.
const prices = [1,5,8,9,10, 17, 17, 20, 24, 30]
function rodsRevenue(n, prices, /* cache ? */) {
// implement this
}
console.log(rodsRevenue(5, prices));Rod cutting problem is very much related to any real-world maximization problem we face.
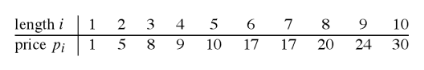
Longest common substring
function lcs(a = '', b = '') {
}
console.log(lcs('asdABCDas', '12345567_ABCD_89')) // ABCDThe longest common subsequence problem is a classic computer science problem, the basis of data comparison programs such as the diff utility, and has applications in bioinformatics. It is also widely used by revision control systems such as Git for reconciling multiple changes made to a revision-controlled collection of files.
Eggs Dropping Puzzle
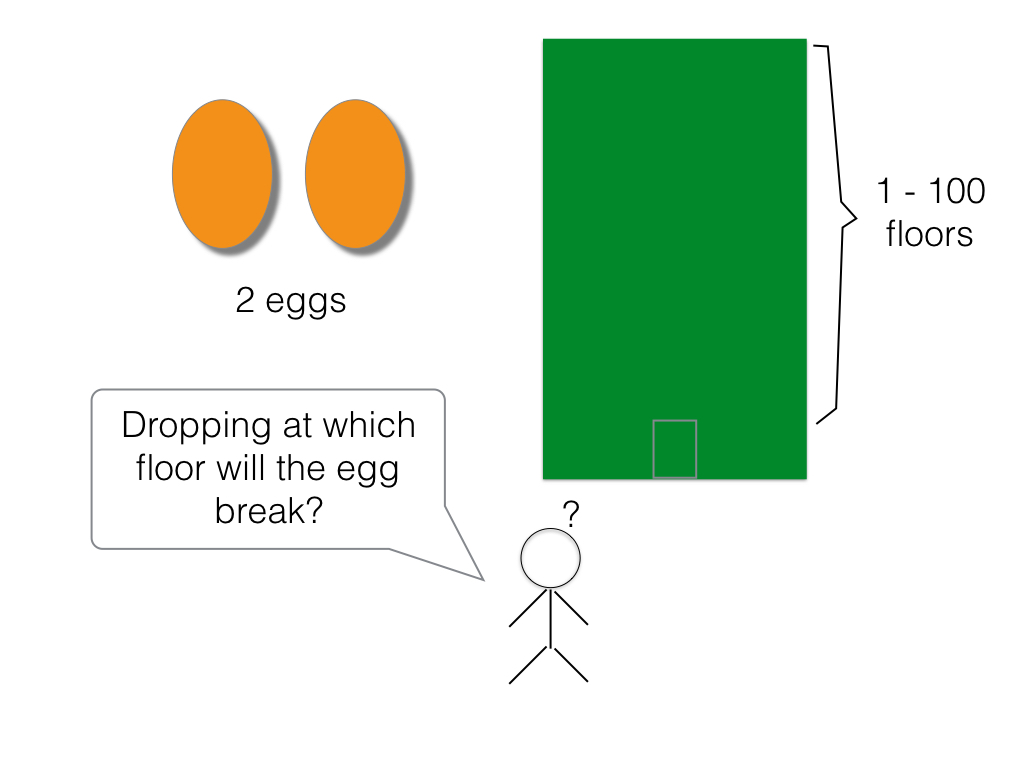
Suppose that we wish to know which stories in a 100-story building are safe to drop eggs from, and which will cause the eggs to break on landing.
We make a few assumptions:
…..An egg that survives a fall can be used again.
…..A broken egg must be discarded.
…..The effect of a fall is the same for all eggs.
…..If an egg breaks when dropped, then it would break if dropped from a higher floor.
…..If an egg survives a fall then it would survive a shorter fall.
…..It is not ruled out that the first-floor windows break eggs, nor is it ruled out that the 100th-floor do not cause an egg to break.
Optimal Substructure
When we drop an egg from a floor x, there can be two cases
(1) The egg breaks
(2) The egg doesn’t break.
1) If the egg breaks after dropping from xth floor, then we only need to check for floors lower than x with remaining eggs; so the problem reduces to x-1 floors and n-1 eggs
2) If the egg doesn’t break after dropping from the xth floor, then we only need to check for floors higher than x; so the problem reduces to k-x floors and n eggs.
eggDrop(n, k) ==> Minimum number of trials needed to find the critical floor in worst case.
k ==> Number of floors n ==> Number of Eggs
eggDrop(n, k) = 1 + min{max(eggDrop(n - 1, x - 1), eggDrop(n, k - x)): x in {1, 2, ..., k}}
Analyzing the problem
function eggDrop(eggs = 2, floors = 10) {
// implement this
}Implement a recursive solution!

function opt(eggs = 2, floors = 10) {
if (floors === 0 || floors === 1 || eggs === 1) return floors;
let min = Infinity;
for (let f = 1; f <= floors; f++) {
const cand = Math.max(opt(eggs - 1, f - 1), opt(eggs, floors - f));
if (cand < min) {
min = cand;
}
}
return min + 1;
}Modify a solution to use dynamic programming concept!
function eggDrop(eggs, floors) {
/* A 2D table where entery eggFloor[i][j] will represent minimum
number of trials needed for i eggs and j floors. */
const eggFloor = Array.from({ length: eggs + 1}, () => []);
let res = Infinity;
// We need one trial for one floor and0 trials for 0 floors
for (let i = 1; i <= eggs; i++) {
eggFloor[i][1] = 1;
eggFloor[i][0] = 0;
}
// We always need j trials for one egg and j floors.
for (j = 1; j <= floors; j++) {
eggFloor[1][j] = j;
}
// Fill rest of the entries in table using optimal substructure property
for (i = 2; i <= eggs; i++) {
for (j = 2; j <= floors; j++) {
eggFloor[i][j] = Infinity;
for (x = 1; x <= j; x++) {
res = 1 + Math.max(eggFloor[i-1][x-1], eggFloor[i][j-x]);
if (res < eggFloor[i][j])
eggFloor[i][j] = res;
}
}
}
// eggFloor[eggs][floors] holds the result
return eggFloor[eggs][floors];
} Another way to use cache (optimal substructure, bottom -> up upproach)
Thank you!

Algorithms #13
By Vladimir Vyshko
Algorithms #13
Dynamic Programming intro
- 770



