Algorithms #2

How to solve this ?
General strategy of solving problems

George Pólya
He was a professor of mathematics from 1914 to 1940 at ETH Zürich and from 1940 to 1953 at Stanford University. He made fundamental contributions to combinatorics, number theory, numerical analysis and probability theory.
General steps
- Understand the Problem
- Explore Concrete Examples
- Break It Down
- Start with a naive solution
- Solve/Simplify
- Look Back and Refactor

- Can I restate the problem in my own words?
- What are the inputs that go into the problem?
- What are the outputs that should come from the solution to the problem?
- Do I have enough information to solve the problem?
Understand the Problem
Lets solve a problem...
Problem #1
Determine whether an integer is a palindrome. An integer is a palindrome when it reads the same backward as forward. with O(1) space, O(k) time complexity. k - num of digits
/* Understand the Problem
* Explore Concrete Examples
* Break It Down
* Writy a naive solution
* Solve/Simplify
* Look Back and Refactor
*/
// Input: 121
// Output: true
//
// Input: -121
// Output: false
//
// Input: 10
// Output: false
function isPalindrome(number) {
}
- Start with Simple Examples
- Progress to More Complex Examples
- Explore Examples with Empty Inputs
- Explore Examples with Invalid Inputs
Explore examples
There are 100 doors and 100 people. The doors have two states (open/closed). All the doors are closed at first. Then the first person opens all the doors, the second person toggles the doors in multiples of 2 (e.g. door 2,4,6..). The third person toggles the doors in multiples of 3 (3,6,9...). This continues until person 100 toggles the door 100. So how many doors are open and how many are closed.
The doors problem
Problem #2

How do you check if two strings are a rotation of each other?
Problem #3

// "abcd" => "cdab" TRUE
// "1234" => "2341" TRUE
Common patterns
Frequency Counter Pattern
It is a very common scenario in many algorithms where you have to compare values from two arrays. Your first thought is to loop over the first array and either use a second inner loop for iterating the second array or use indexOf array method for the
second array. The essential problem with these is performance , since as the size of the arrays increases, performance suffers.
Write a function which accepts two arrays and returns true if every value in array1 has corresponding value squared in array2. The frequency of the values should also match for the function to return true.
Problem #4

How do you check if two strings are anagrams of each other?
Problem #5

Two Pointers
Two pointers is really an easy and effective technique which is typically used for searching pairs in a sorted array.
We take two pointers, one representing the first element and other representing the last element of the array, and then we add the values kept at both the pointers.
Given a sorted array A (sorted in ascending order), having N integers, find if there exists any pair of elements (A[i], A[j]) such that their sum is equal to X.
Problem #6
isSubsequence
Problem #7
Write a function called isSubsequence which takes in two strings and checks whether the characters in the first string form a subsequence of the characters in the second string.
In other words, the function should check whether the characters in the first string appear somewhere in the second string, without their order changing.
isSubsequence('abc', 'a1b2c3') // true
isSubsequence('abc', 'aaaabbbbcccc') // true
isSubsequence('abc', 'acb') // falseWindow Sliding
This technique shows how a nested for loop in few problems can be converted to single for loop and hence reducing the time complexity.
The technique can be best understood with the window pane in bus, consider a window of length n and the pane which is fixed in it of length k.
Problem #8
Given an array of integers of size ‘n’. Our aim is to calculate the maximum sum of ‘k’ consecutive elements in the array.
Input : arr = [100, 200, 300, 400]
k = 2
Output : 700Applying sliding window technique :
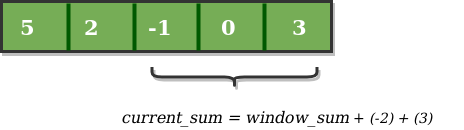
- We compute the sum of first k elements out of n terms using a linear loop and store the sum in variable window_sum.
- Then we will graze linearly over the array till it reaches the end and simultaneously keep track of maximum sum.
- To get the current sum of block of k elements just subtract the first element from the previous block and add the last element of the current block .


Problem #9
minSubArrayLen([2,3,1,2,4,3], 7) // 2 -> because [4,3] is the smallest subarray
minSubArrayLen([2,1,6,5,4], 9) // 2 -> because [5,4] is the smallest subarray
minSubArrayLen([3,1,7,11,2,9,8,21,62,33,19], 52) // 1 -> because [62] is greater than 52
minSubArrayLen([1,4,16,22,5,7,8,9,10],39) // 3
minSubArrayLen([1,4,16,22,5,7,8,9,10],55) // 5
minSubArrayLen([4, 3, 3, 8, 1, 2, 3], 11) // 2
minSubArrayLen([1,4,16,22,5,7,8,9,10],95) // 0Write a function called minSubArrayLen which accepts two parameters - an array of positive integers and a positive integer.
This function should return the minimal length of a contiguous subarray of which the sum is greater than or equal to the integer passed to the function. If there isn't one, return 0 instead. Time Complexity - O(n) Space Complexity - O(1)

THE DIVIDE AND CONQUER PATTERN
Divide and conquer (D&C) is an algorithm design paradigm based on multi-branched recursion. A divide and conquer algorithm works by recursively breaking down a problem into two or more sub-problems of the same or related type, until these become simple enough to be solved directly.
The solutions to the sub-problems are then combined to give a solution to the original problem.
Example: Merge Sort


fib
Problem #10
Write a recursive function called fib which accepts a number and returns the nth number in the Fibonacci sequence. Recall that the Fibonacci sequence is the sequence of whole numbers 1, 1, 2, 3, 5, 8, ... which starts with 1 and 1, and where every number thereafter is equal to the sum of the previous two numbers.
Homework
1. Write an algorithm to determine if a number n is "happy". [Caching + digits sum]
2. Longest Substring Without Repeating Characters [ Sliding window / caching ]

Introduction to Algorithms
by Thomas H. Cormen (Author)
Thank You!

Algorithms #2
By Vladimir Vyshko
Algorithms #2
Strategies of solving interview tasks
- 935



