Algorithms #3

Searching algorithms

Searching algorithms

Searching Algorithms are designed to check for an element or retrieve an element from any data structure where it is stored. Based on the type of search operation, these algorithms are generally classified into two categories:

  1. Sequential Search: In this, the list or array is traversed sequentially and every element is checked. For example: Linear Search.
  2. Interval Search: These algorithms are specifically designed for searching in sorted data-structures. These type of searching algorithms are much more efficient than Linear Search as they repeatedly target the center of the search structure and divide the search space in half. For Example: Binary Search.

Linear Search

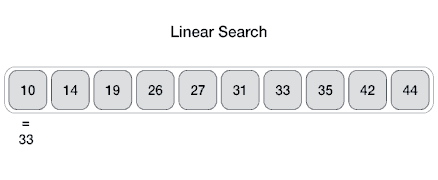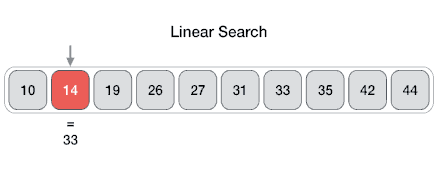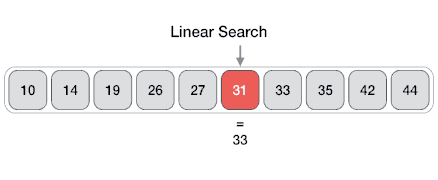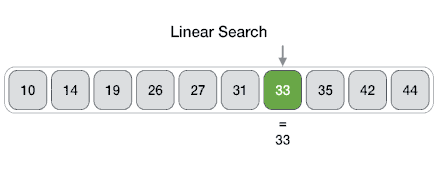
In computer science, a linear search or sequential search is a method for finding an element within a list. It sequentially checks each element of the list until a match is found or the whole list has been searched.

Use cases of Linear Search

  1. The list is unsorted and is only to be searched once

  2. The list is small (though this itself is a vague notion - I've read less than around 100 elements?)

  3. The list will need sorting following the search operation (due to say an insertion), since the resorting will dominate the time complexity of the overall task

  4. The data structure is not random access (like a linked-list)

  5. There is no knowledge of the data that could aid searching (relative proximities?)

Linear Search already implemented for you

[{ x: 1 }, { x: 2, target: 'searching this one' }, { x: 3 } ]
   .find(el => el.x === 2); // { x: 2, target=... }

Lets try to implement it using for loop...

Problem #1

Implement our own .linearSearch(comparator) function on array prototype, so we can search elements on array in same way like .find works:

 

[{x: 10, data: "bacon"}, { x: 20, data: "tuna" }, {x: 30, data: "cucumber"}]
	.linearSearch(element => element.data === "tuna"); 
    // should return { x: 20, data: "tuna" }

Problem #2

Implement our own recursiveLinearSearch(comparator) function, so we can search without iterating elements with for/while loop but with recursion.

 

Improve linear search ?

Sentinel Linear Search

Sentinal Linear Search as the name suggests is a type of Linear Search where the number of comparisons are reduced as compared to a traditional linear search.

//standard linear search
for (let i = 0; i < length; i++) {
    if (array[i] === elementToSearch) {
        return i; // I found the position of the element requested
    }
}


// sentinel search
const lastIndex = array.length - 1;
const lastElement = array[lastIndex]; // save last element
array[lastIndex] = elementToSearch; // replace last element with searched value

let i = 0;
while(array[i] !== elementToSearch) {
    i++;
}
    
if (i === lastIndex) {
   return lastElement === elementToSearch ? element : -1;
}

return arr[i]

Sentinel 

Ok, what if array sorted ?

  • Binary Search

    • Exponential Search

    • Fibonacci Search

    • Interpolation Search

    • ...

  • Jump Search

  • ...

Binary Search

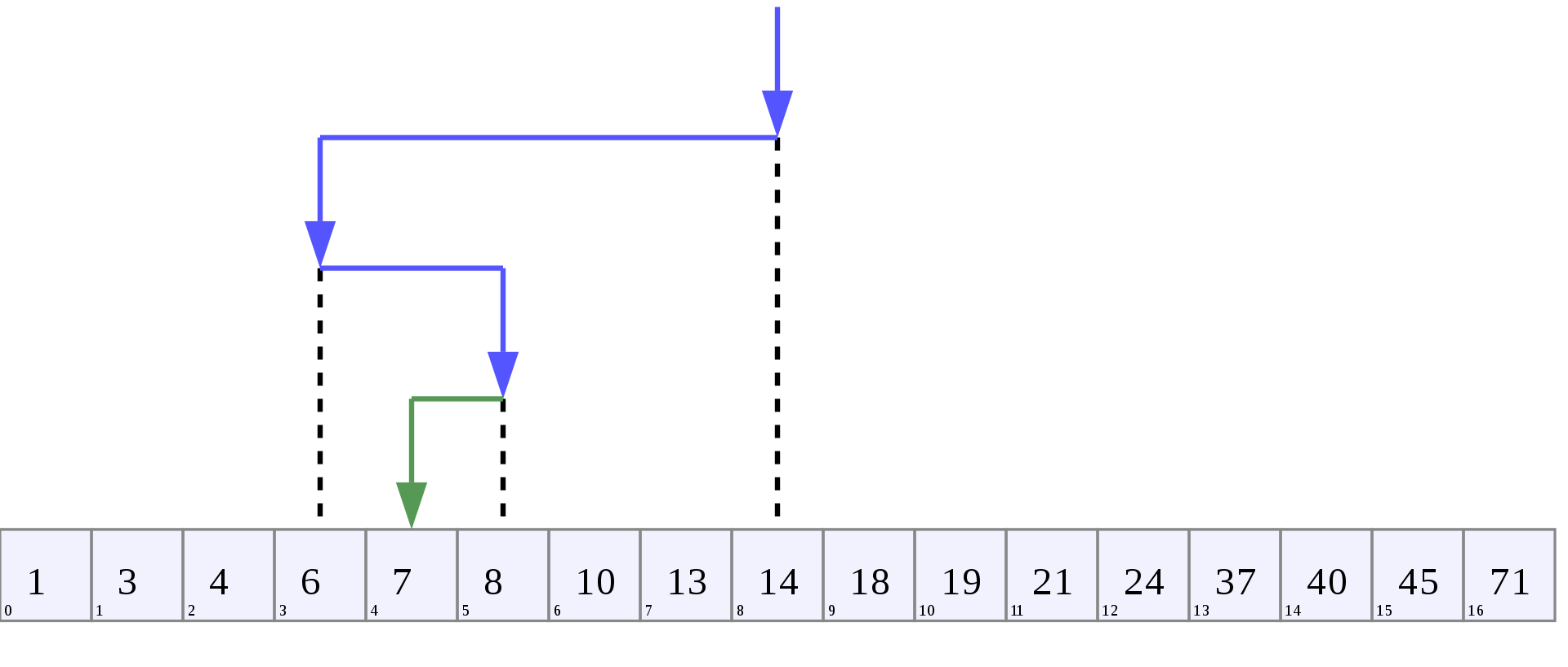
Classic recursive algorithm

Target

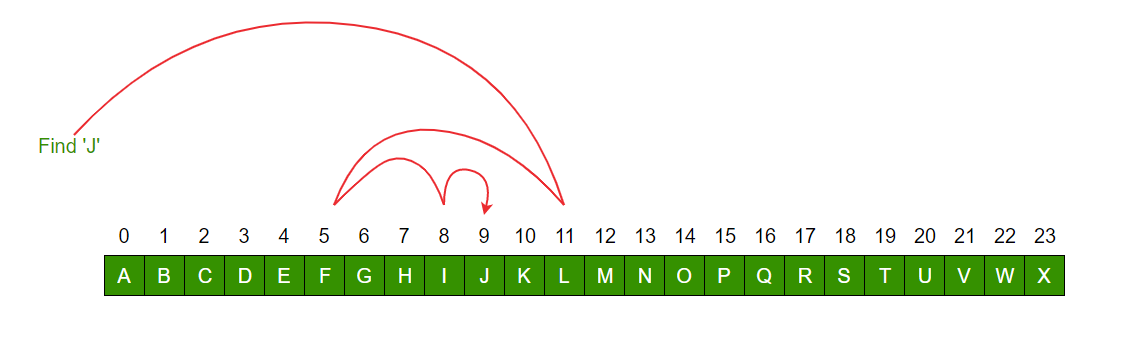
Cut down your search to half as soon as you find middle of a sorted list.

  1. The middle element is looked to check if it is greater than or less than the value to be searched.
  2. Accordingly, search is done to either half of the given list

Problem #3

Implement recursive binary search algorithm

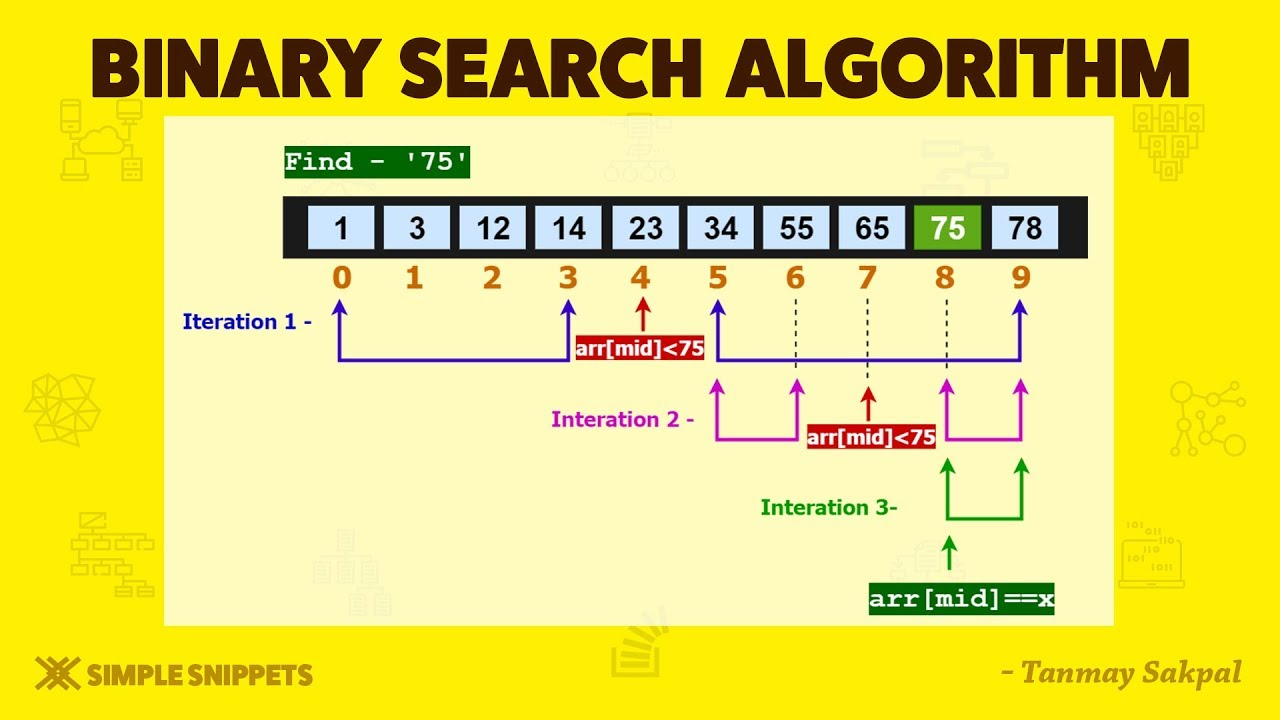
Problem #4

Implement iterative binary search algorithm

Recursive vs Iterative ?

So, which method is best? Well, obviously it depends on what you're trying to do - not all processes will provide an obvious recursive solution. Where they exist, recursive solutions tend to be more elegant, but can potentially be more difficult to understand (an important point to bear in mind if other people are going to be maintaining your code).

Recursive functions may also be executed more slowly (depending on your environment). Each time a function is called, certain values are placed onto the stack - this not only takes time, but can eat away at your resources if your function calls itself many times. In extreme examples you could run out of stack space. Functions that just iterate make no such demands on stack space, and may be more efficient where memory is limited.

What if we have repeated values ?

Say we wonna to implement dictionary and sequance is metter ?

[0,1,2,2,2,2,2,3,4,5,6]

Search first appeared value

Leftmost binary search

Problem #4

Implement leftmost binary search

Problem #5

 A sorted array has been rotated so that the elements might appear in the order [3, 4, 5, 6, 7, 1, 2]. How would you find the minimum element?

Algorithm

  • Finding the minimum element in an array isn’t a particularly interesting algorithm (you could just iterate through all the elements), nor does it use the information provided (that the array is sorted). It’s unlikely to be useful here.
  • However, binary search is very applicable. You know that the array is sorted, but rotated. So, it must proceed in an increasing order, then reset and increase again. The minimum element is the “reset” point.
  • If you compare the first and middle element (3 and 6), you know that the range is still increasing. This means that the reset point must be after the 6 (or, 3 is the minimum element and the array was never rotated). We can continue to apply the lessons from binary search to pinpoint this reset point, by looking for ranges where LEFT > RIGHT. That is, for a particular point, if LEFT < RIGHT, then the range does not contain the reset. If LEFT > RIGHT, then it does.

Fibonacci search ?

Similarities with Binary Search:

  1. Works for sorted arrays
  2. A Divide and Conquer Algorithm.
  3. Has Log n time complexity.

 

Differences with Binary Search:

  1. Fibonacci Search divides given array in unequal parts
  2. Binary Search uses division operator to divide range. Fibonacci Search doesn’t use /, but uses + and -. The division operator may be costly on some CPUs.
  3. Fibonacci Search examines relatively closer elements in subsequent steps. So when input array is big that cannot fit in CPU cache or even in RAM, Fibonacci Search can be useful.

Interpolation search ?

Interpolation search

Algorithm
Rest of the Interpolation algorithm is the same except the above partition logic.

Step1: In a loop, calculate the value of “pos” using the probe position formula.
Step2: If it is a match, return the index of the item, and exit.
Step3: If the item is less than arr[pos], calculate the probe position of the left sub-array. Otherwise calculate the same in the right sub-array.
Step4: Repeat until a match is found or the sub-array reduces to zero.

Interpolation search

// WE DEVIDE ARRAY IN TWO PARTS IN SAME WAY LIKE IN BINARY SEARCH, BUT
// The idea of formula is to return higher value of pos
// when element to be searched is closer to arr[hi]. And
// smaller value when closer to arr[lo]
pos = lo + [ (x-arr[lo])*(hi-lo) / (arr[hi]-arr[Lo]) ]

arr[] ==> Array where elements need to be searched
x     ==> Element to be searched
lo    ==> Starting index in arr[]
hi    ==> Ending index in arr[]

Time Complexity: If elements are uniformly distributed, then O (log log n)). In worst case it can take up to O(n).
Auxiliary Space: O(1)

Exponential Search ?

Exponential Search

The name of this searching algorithm may be misleading as it works in O(Log n) time. The name comes from the way it searches an element.

Exponential search involves two steps:

  1. Find range where element is present
  2. Do Binary Search in above found range.

Exponential Search

function exponentialSearch(arr = [], n, x) 
    { 
        // If x is present at firt location itself 
        if (arr[0] === x) 
            return 0; 
      
        // Find range for binary search by 
        // repeated doubling 
        let i = 1; 
        while (i < n && arr[i] <= x) 
            i = i*2; 
      
        // Call binary search for the found range. 
        return binarySearch(arr, i/2, Math.min(i, n), x); 
    }

Jump search ?

Jump search

Important points:

  • Works only sorted arrays.
  • The optimal size of a block to be jumped is (√ n). This makes the time complexity of Jump Search O(√ n).
  • The time complexity of Jump Search is between Linear Search ( ( O(n) ) and Binary Search ( O (Log n) ).
  • Binary Search is better than Jump Search, but Jump search has an advantage that we traverse back only once (Binary Search may require up to O(Log n) jumps, consider a situation where the element to be searched is the smallest element or smaller than the smallest). So in a system where binary search is costly, we use Jump Search.

There is no best searching algorithm for all cases!

You should choose algorithm depending on your data and computing spec

Homework

Is Subsequence
Given a string s and a string t, check if s is subsequence of t.
https://leetcode.com/problems/is-subsequence/

Search in Rotated Sorted Array
Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.You are given a target value to search.
https://leetcode.com/problems/search-in-rotated-sorted-array/
 

Cracking the Coding Interview

by Gayle Laakmann McDowell  (Author)

http://ahmed-badawy.com/blog/wp-content/uploads/2018/10/Cracking-the-Coding-Interview-6th-Edition-189-Programming-Questions-and-Solutions.pdf

Thank you!

Links

https://www.quora.com/Which-is-the-best-algorithm-for-searching - Which is the best algorithm for searching?

https://www.geeksforgeeks.org/linear-search/ - Linear Search

https://www.geeksforgeeks.org/binary-search/ - Binary Search
 

https://en.wikipedia.org/wiki/Binary_search_algorithm#Procedure_for_finding_the_leftmost_element - Leftmost BS

https://sites.google.com/site/binarysearchcube/binary-search - BS variations

https://habr.com/ru/post/91605/ - Только 10% программистов способны написать двоичный поиск

Algorithms #3

By Vladimir Vyshko

Made with Slides.com

Algorithms #3

Binary search, linear search, and others

  • 557

More from Vladimir Vyshko