Algorithms #5

faster sorts
Sorting algorithms in programming languages
- C’s qsort() – Quicksort
- C++’s sort() – Introsort (Hybrid of Quicksort, Heap Sort and Insertion Sort)
- C++’s stable_sort() – Mergesort
- Java 6’s Arrays.sort() – Quicksort
- Java 7’s Arrays.sort() – Timsort (Hybrid of Mergesort and Insertion Sort)
- Java’s Collections.sort() – Mergesort
- Python’s sorted() – Timsort (Hybrid of Mergesort and Insertion Sort)
- Python’s sort() – Timsort (Hybrid of Mergesort and Insertion Sort)
- JavaScript v8 .sort(fn) - Timsort
Insertion sort
Quck Sort
Merge Sort
Quick Sort




Quick Sort

QuickSort is a Divide and Conquer algorithm. It picks an element as pivot and partitions the given array around the picked pivot. There are many different versions of quickSort that pick pivot in different ways.
Quick Sort Algorithm
1. Find index of pivot element (middle index)
2. Place all values that smaller then pivot on left side before pivot
3. Return final pivot index
4. Recusivly repeat same operation on array left part (before pivot)
5. Recusivly repeat same operation on array right part (starting from pivot)
}
Partition function

Quick Sort (Hoare partition )



Quick Sort Partition
Hoare partition scheme
Lomuto partition scheme
Less operations
Less code
The basic Lomuto partition scheme swaps the pivot out of the way, does the partition, swaps the pivot into place and then returns an index to the pivot at its sorted position. In this case, the pivot can be excluded from the recursive calls:
The basic Hoare partition scheme scans from both ends towards some point within the partition, putting all elements less than the pivot to the left of all elements greater than the pivot, but any elements equal to the pivot, including the pivot itself, can end up anywhere in the partition, and the index returned is the split point between the left (elements <= pivot) and right (elements >= pivot), so the calling code cannot exclude the element at the index returned from Hoare partition function from recursive calls. If the Hoare scheme is modified to be similar to Lomuto, where it swaps the pivot to either end, does the partition, then swaps the pivot to the split index, then the calling code can exclude the pivot, but this ends up being slower.
Difference
Quick Sort

Problem #1
Implement QuickSort

Pivot can be selected from any index
Pivot is first element:
Merge Sort




Merge Sort
Like QuickSort, Merge Sort is a Divide and Conquer algorithm. It divides input array in two halves, calls itself for the two halves and then merges the two sorted halves. The merge() function is used for merging two halves. The merge(arr, l, m, r) is key process that assumes that arr[l..m] and arr[m+1..r] are sorted and merges the two sorted sub-arrays into one. See following C implementation for details.
Merge Sort
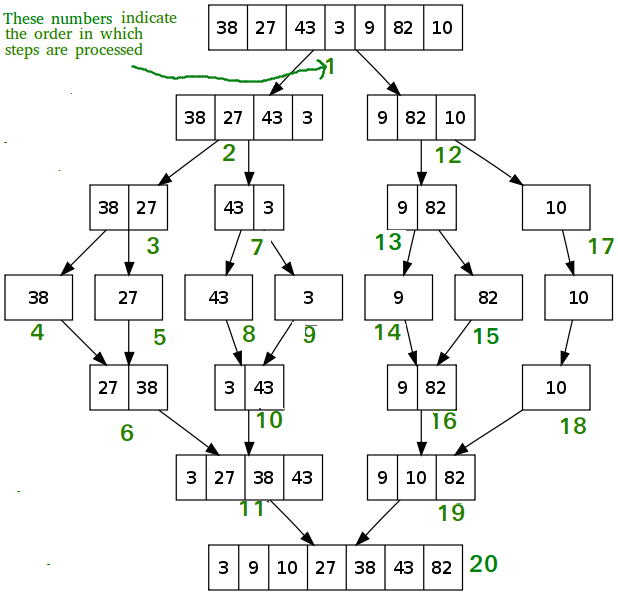
Merge Sort Algorithm
MergeSort(arr[], l, r)
If r > l
1. Find the middle point to divide the array into two halves:
middle m = (l+r)/2
2. Call mergeSort for first half:
Call mergeSort(arr, l, m)
3. Call mergeSort for second half:
Call mergeSort(arr, m+1, r)
4. Merge the two halves sorted in step 2 and 3:
Call merge(arr, l, m, r)

Problem #2
Implement merge function
merge([1,10], [2, 20]) // => [1,2,10,20]
merge([1], [2, 3, 4, 5, 6]) // => [1,2,3,4,5,6]Problem #3
Implement mergeSort function
mergeSort([1,10, 2, 20]) // => [1,2,10,20]

Merge Sort
Merge Sort

Recommendations:
Quick sort: When you don't need a stable sort and average case performance matters more than worst case performance. A quick sort is O(N log N) on average, O(N^2) in the worst case. A good implementation uses O(log N) auxiliary storage in the form of stack space for recursion.
Merge sort: When you need a stable, O(N log N) sort, this is about your only option. The only downsides to it are that it uses O(N) auxiliary space and has a slightly larger constant than a quick sort. There are some in-place merge sorts, but AFAIK they are all either not stable or worse than O(N log N). Even the O(N log N) in place sorts have so much larger a constant than the plain old merge sort that they're more theoretical curiosities than useful algorithms.
Radix Sort
Faster then n*log(n) ???
Radix Sort
The idea of Radix Sort is to do digit by digit sort starting from least significant digit to most significant digit. Radix sort uses counting sort as a subroutine to sort.
Radix Sort
The Radix Sort Algorithm
1) Do following for each digit i where i varies from least significant digit to the most significant digit.
………….a) Sort input array using counting sort (or any stable sort) according to the i’th digit.
Example:
Original, unsorted list:
170, 45, 75, 90, 802, 24, 2, 66
Sorting by least significant digit (1s place) gives: [*Notice that we keep 802 before 2, because 802 occurred before 2 in the original list, and similarly for pairs 170 & 90 and 45 & 75.]
170, 90, 802, 2, 24, 45, 75, 66
Sorting by next digit (10s place) gives: [*Notice that 802 again comes before 2 as 802 comes before 2 in the previous list.]
802, 2, 24, 45, 66, 170, 75, 90
Sorting by most significant digit (100s place) gives:
2, 24, 45, 66, 75, 90, 170, 802
The Radix Sort Algorithm
1) Do following for each digit i where i varies from least significant digit to the most significant digit.
………….a) Sort input array using counting sort (or any stable sort) according to the i’th digit.
Example:
Original, unsorted list:
170, 45, 75, 90, 802, 24, 2, 66
Sorting by least significant digit (1s place) gives: [*Notice that we keep 802 before 2, because 802 occurred before 2 in the original list, and similarly for pairs 170 & 90 and 45 & 75.]
170, 90, 802, 2, 24, 45, 75, 66
Sorting by next digit (10s place) gives: [*Notice that 802 again comes before 2 as 802 comes before 2 in the previous list.]
802, 2, 24, 45, 66, 170, 75, 90
Sorting by most significant digit (100s place) gives:
2, 24, 45, 66, 75, 90, 170, 802
Radix Sort
Advantages :
1. Fast when the keys are short i.e. when the range of the array elements is less.
2. Used in suffix array constuction algorithms like Manber's algorithm and DC3 algorithm.
Disadvantages:
1. Since Radix Sort depends on digits or letters, Radix Sort is much less flexible than other sorts. Hence , for every different type of data it needs to be rewritten.
2. The constant for Radix sort is greater compared to other sorting algorithms.
3. It takes more space compared to Quicksort which is inplace sorting.
The Radix Sort algorithm is an important sorting algorithm that is integral to suffix -array construction algorithms. It is also useful on parallel machines.
function numberOfDigits(num) { // O(1)
if (num === 0) return 1;
return Math.floor(Math.log10(Math.abs(num))) + 1;
}
function getDigit(num, pos) { // O(1)
return Math.floor(Math.abs(num) / Math.pow(10, pos)) % 10
}
function mostDigits(arr = []) { // O(n)
return arr.reduce((max, cur) => Math.max(max, numberOfDigits(cur)), 0)
}
function radixSort(arr) {... }Problem #4
Radix Sort
Recap

Thank you!

Module #1: owned
Links
https://cs.stackexchange.com/questions/11458/quicksort-partitioning-hoare-vs-lomuto - Quicksort Partitioning: Hoare vs. Lomuto
https://www.hackerearth.com/ru/practice/algorithms/sorting/radix-sort/tutorial/ - radix sort tutorial
https://www.geeksforgeeks.org/merge-sort/ - merge sort
Algorithms #5
By Vladimir Vyshko
Algorithms #5
Merge Sort, Quick Sort, Radix sort
- 919



