Algorithms #9

Trees

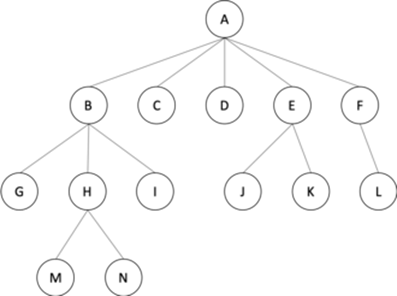
What is a tree datastructure ?

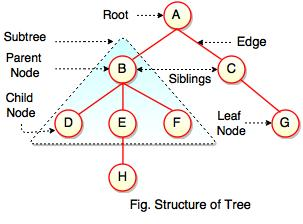
Root

Nodes

Leaf

  • Tree is a hierarchical data structure which stores the information naturally in the form of hierarchy style.
  • Tree is one of the most powerful and advanced data structures.
  • It is a non-linear data structure compared to arrays, linked lists, stack and queue.
  • It represents the nodes connected by edges.

Terminology summary

  • Root is the topmost node of the tree
  • Edge is the link between two nodes
  • Child is a node that has a parent node
  • Parent is a node that has an edge to a child node
  • Leaf is a node that does not have a child node in the tree
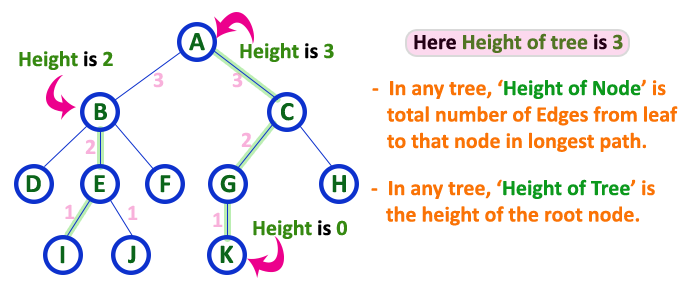
  • Height is the length of the longest path to a leaf

Trees in real world

1. DOM Tree

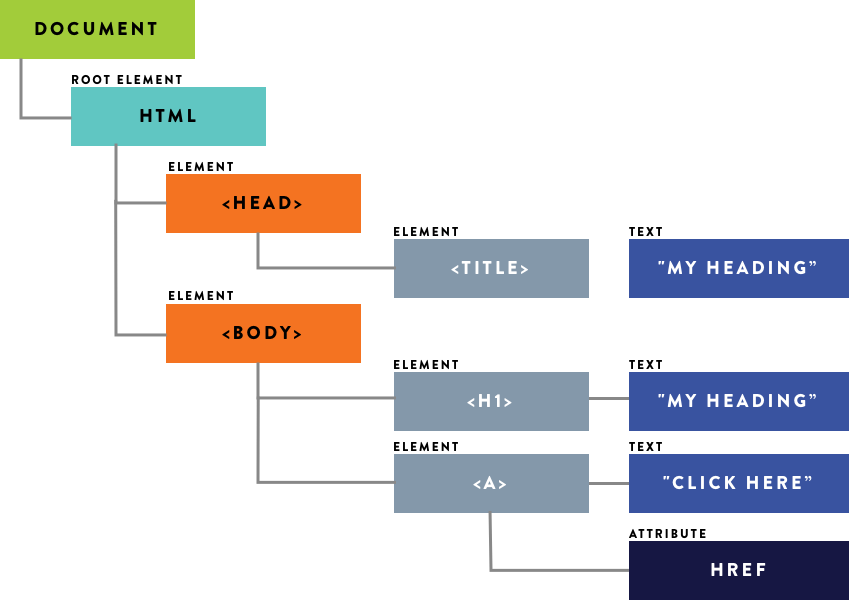
When a web page is loaded, the browser creates a Document Object Model of the page. The HTML DOM model is constructed as a tree of Objects. With HTML DOM, JavaScript can access and change all the elements of an HTML document

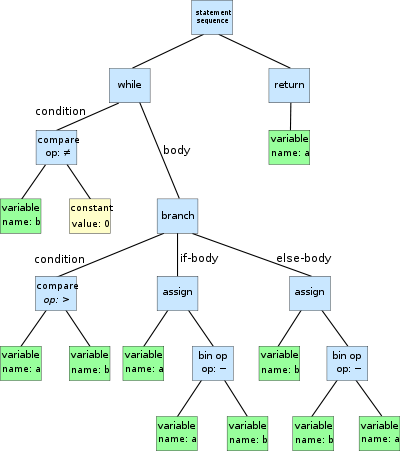
2. AST

In computer science, an abstract syntax tree (AST), or just syntax tree, is a tree representation of the abstract syntactic structure of source code written in a programming language.

https://astexplorer.net/

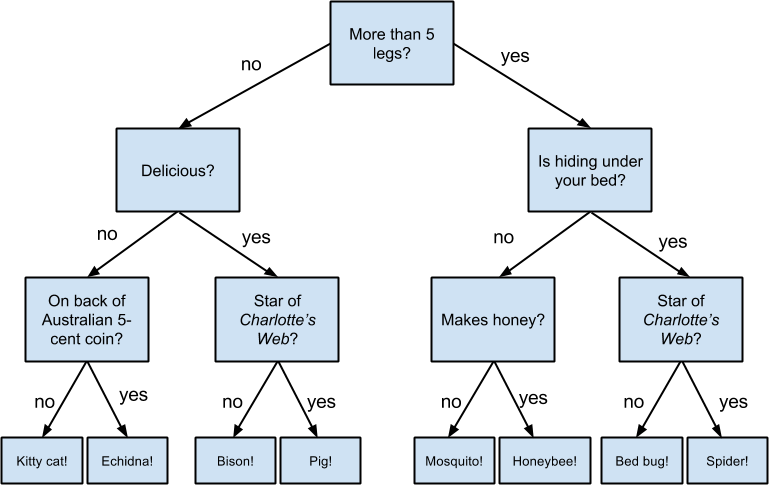
3. Decision trees

Decision tree is one of the most popular machine learning algorithms used all along. A decision tree is a tree where each node represents a feature(attribute), each link(branch) represents a decision(rule) and each leaf represents an outcome(categorical or continues value).

akinator.com

And many more...

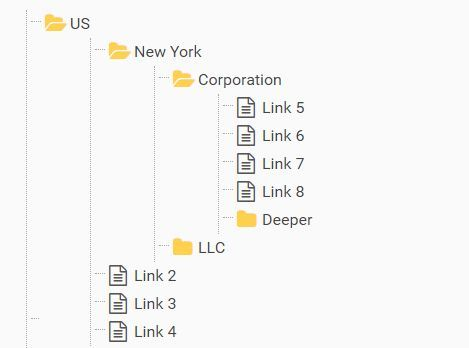
File structure model

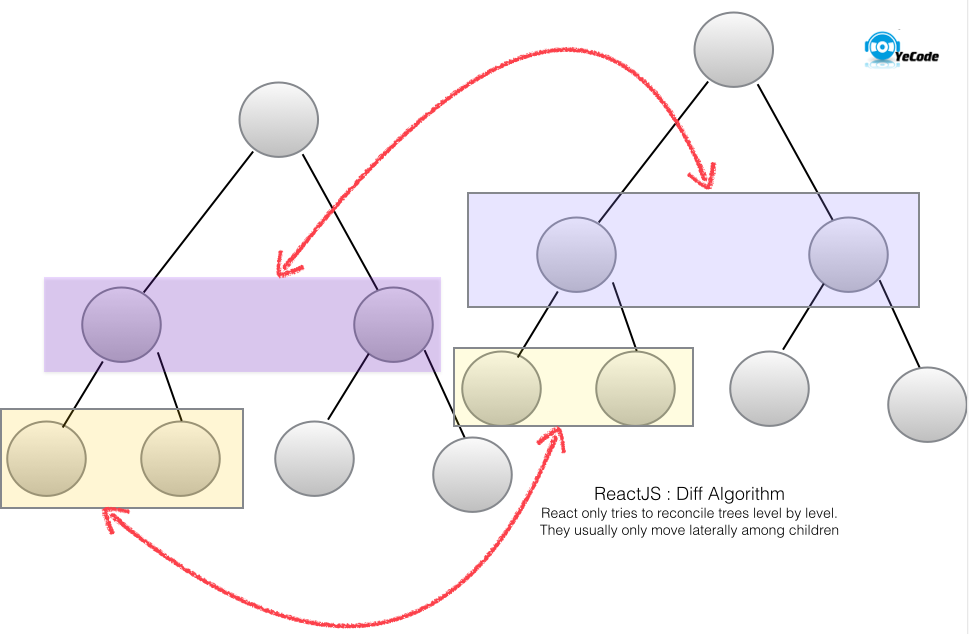
React fiber reconscilation

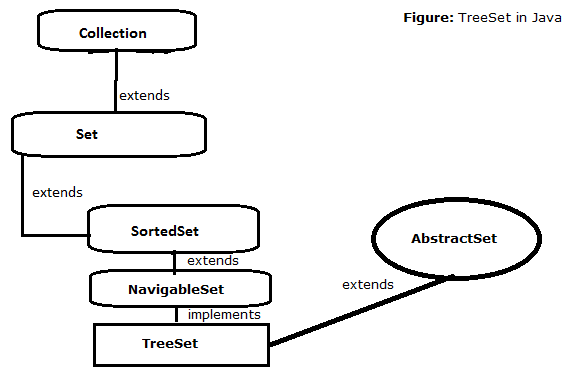
Implementing other datastructures: TreeSet, PriorityQueue...

Real world buisness logic

Types of trees

overview

Binary Tree

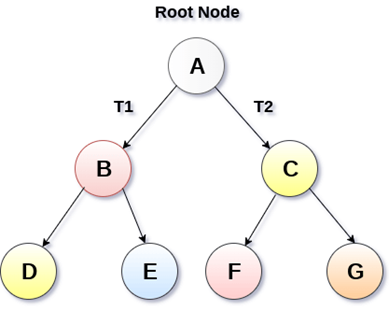
Binary tree is the type of tree in which each parent can have at most two children. The children are referred to as left child or right child. This is one of the most commonly used trees. When certain constraints and properties are imposed on Binary tree it results in a number of other widely used trees like BST (Binary Search Tree), AVL tree, RBT tree etc.

Binary Search Tree

Binary Search Tree (BST) is an extension of Binary tree with some added constraints. In BST, the value of the left child of a node must be smaller than or equal to the value of its parent and the value of the right child is always larger than or equal to the value of its parent. This property of Binary Search Tree makes it suitable for searching operations as at each node we can decide accurately whether the value will be in left subtree or right subtree. Therefore, it is called a Search Tree.

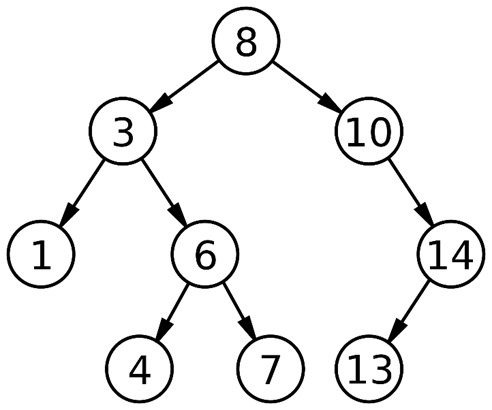
AVL Tree

AVL tree is a self-balancing binary search tree. The name AVL is given on the name of its inventors Adelson-Velshi and Landis. This was the first dynamically balancing tree. In AVL tree, each node is assigned a balancing factor based on which it is calculated whether the tree is balanced or not. In AVL tree, the heights of children of a node differ by at most 1. The valid balancing factor in AVL tree are 1, 0 and -1.  When a new node is added to the AVL tree and tree becomes unbalanced then rotation is done to make sure that the tree remains balanced. The common operations like lookup, insertion and deletion takes O(log n) time in AVL tree. It is widely used for Lookup operations.

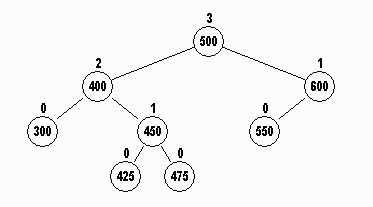
Red-Black Tree

Red-Black is another type of self-balancing tree. The name Red-Black is given to it because each node in a Red-Black tree is either painted Red or Black according to the properties of the Red- Black Tree. This make sure that the tree remains balanced. Although the Red-Black tree is not a perfectly balanced tree but its properties ensure that the searching operation takes only O(log n) time. Whenever a new node is added to the Red-Black Tree, the nodes are rotated and painted again if needed to maintain the properties of the Red-Black Tree .

A red-black tree is a binary search tree which has the following red-black properties:

  • Every node is either red or black.
  • Every leaf (NULL) is black.
  • If a node is red, then both its children are black.
  • Every simple path from a node to a descendant leaf contains the same number of black nodes.

N-ary Tree

In an N-ary tree, the maximum number of children that a node can have is limited to N. A binary tree is 2-ary tree as each node in binary tree has at most 2 children. Trie data structure is one of the most commonly used implementation of N-ary tree. A full N-ary tree is a tree in which children of a node is either 0 or N. A complete N-ary tree is the tree in which all the leaf nodes are at the same level.

And few more...

You don't need to know everything!

Lets try to implement a BST

Why BST ?

  1. Implementing routing table in router. (IP address lookup for internet routers using balanced binary search on routing tables)
  2. Data compression code
  3. Implementation of Expression parsers and expression solvers
  4. To solve database problem such as indexing.
  5. Expression evaluation
  6. BST used in Unix kernels for managing a set of virtual memory areas (VMAs).
  7. Its a good datastructure to get concept of trees !
     
class BinarySearchTree {
    constructor() {
        this.root = null;
    }
    // Add new Node with {value}
    add(value) {
        //...
    }

    // Find Node with {value}
    find(value) {
        //...
    }

    // Check if Node with {value} exists
    contains(value) {
        //...
    }

    depthTraverseRecursive() {
        // DFS
    }

    depthTraverseIterative() {
        // DFS
    }

    breadthTraverse() {
        // BFS
    }

    height(node) {
        // calc height
    }

	//  determine if it is height-balanced.
    isBalanced() {
        // Balanced - a binary tree in which the left and right subtrees of every node differ in height by no more than 1.
    }
}

const tree = new BinarySearchTree();
tree.add(5).add(2).add(-1).add(6).add(100);

// console.log(tree);

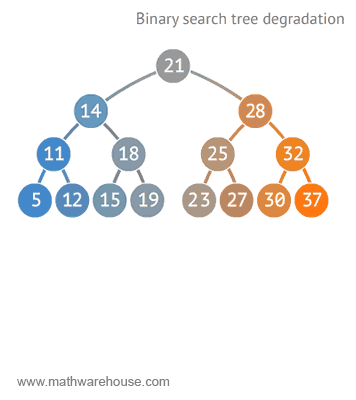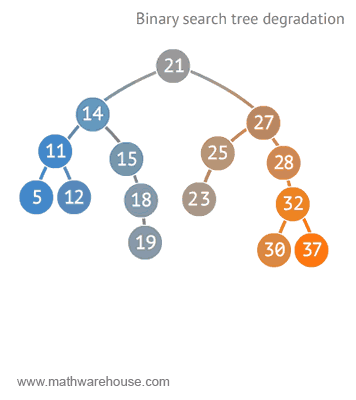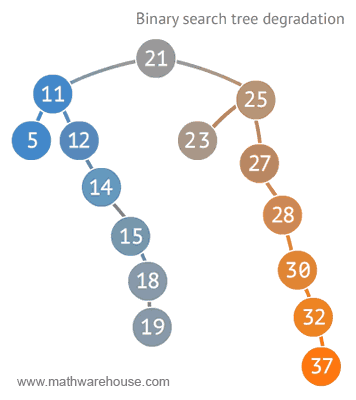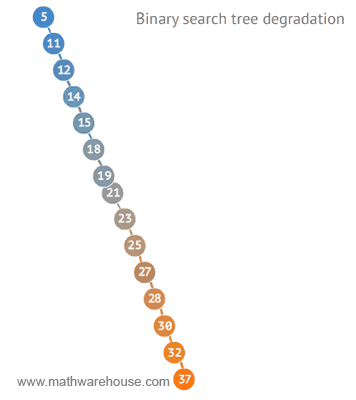
Worst case ?

How to fix degradated tree ?

Thank You!

Algorithms #9

By Vladimir Vyshko

Made with Slides.com

Algorithms #9

Trees overview, BST

  • 503

More from Vladimir Vyshko