Strings
-校培 edition-
關於講師與他的廢話
- 王以安
- 又藍又笨,甚麼都做不好
- 不會字串所以當字串講師
- 過一年還是不會字串
- 段考要燒了
- 簡報字體大小詭譎,請多見諒
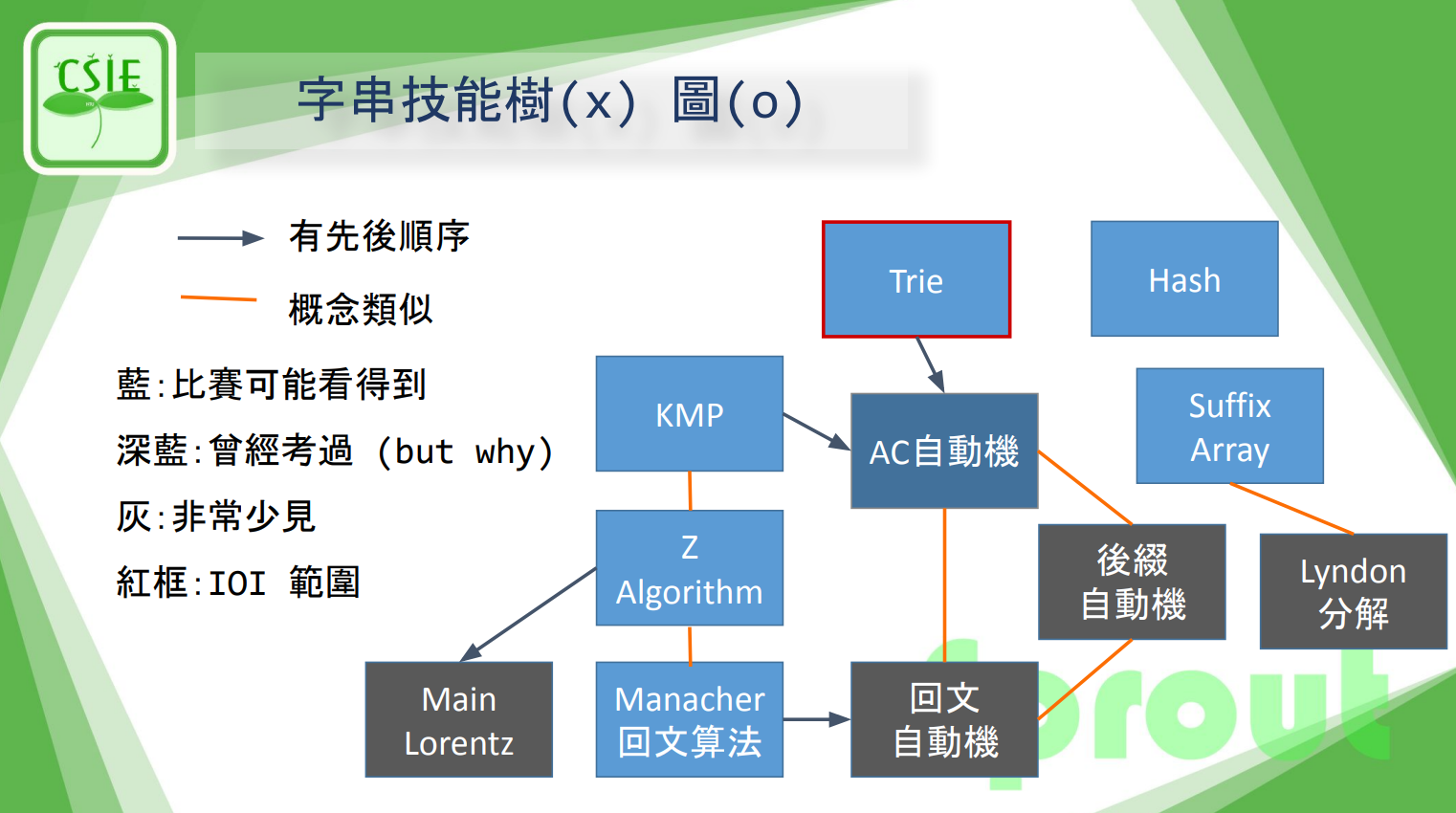
藍色的都會講到
一些約定
- 字串的代號會用\(s,t\)
- 字串的長度會用\(|s|或n\)表示
- 字串和陣列的第i項會用\(a[i]或a_i\)表示
- \(s的k\)前綴代表\(s[0\) : \(k-1]\)
- \(s的k\)後綴代表\(s[n-k\) : \(n-1]\)
- 真前綴就是除了|s|前綴以外的所有前綴
Hash
中文叫雜湊
為什麼需要這個
字串太長不好比較
我們希望透過一個函數把一個字串變成一個數字
這樣看到兩個函數值不一樣,就知道兩個字串不一樣
$$a=f(s)$$
$$這個f就是雜湊函數,a就是雜湊值$$
兩個不同字串對到同個值,則稱兩個字串碰撞了
所以怎麼做?
$$把字串壓成數字(加密),a是1,z是26$$
$$p進位,模M$$
$$p是>26的小(質)數(如31,127,257),M是大(質)數(如998244353)$$
a b c b g
$$例 : 設p=31, M=127$$
1 2 3 2 7
× × × × ×
\(p^0\) \(p^1\) \(p^2\) \(p^3\) \(p^4\)
\(1*1+2*31+3*961+2*29791+7*923521=6527175\)
這個字串的hash值就是6527175模127,也就是10
"abcbg"和"j"碰撞了
a b c b g
反過來也是行的,但值不一樣
1 2 3 2 7
× × × × ×
\(p^4\) \(p^3\) \(p^2\) \(p^1\) \(p^0\)
\(1*923521+2*29791+3*961+2*31+7*1=986055\)
\(986055 ≡ 27 (mod 127)\)
子字串
用前綴和的方式
再除(or乘)上一個\(p\)的冪次使得每個子字串第一個字元乘的數是固定的
子字串
用前綴和的方式
再除(or乘)上一個\(p\)的冪次使得每個子字串第一個字元乘的數是固定的
舉例: 問[1,3]和[0,2]是否一樣,[1,3]是誰?
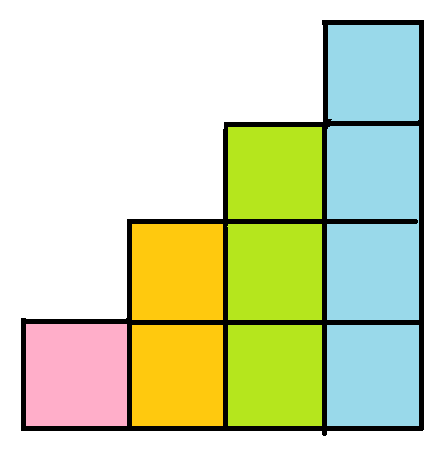
子字串
用前綴和的方式
再除(or乘)上一個\(p\)的冪次使得每個子字串第一個字元乘的數是固定的
舉例: 問[1,3]和[0,2]是否一樣,[1,3]是誰?
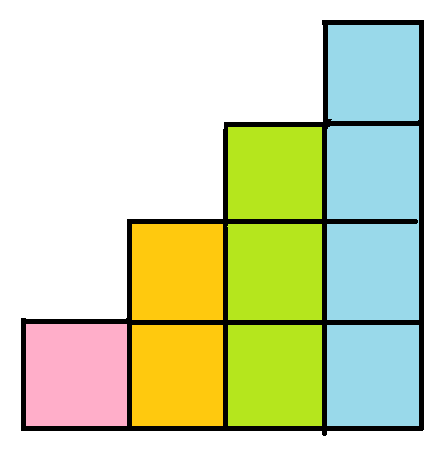
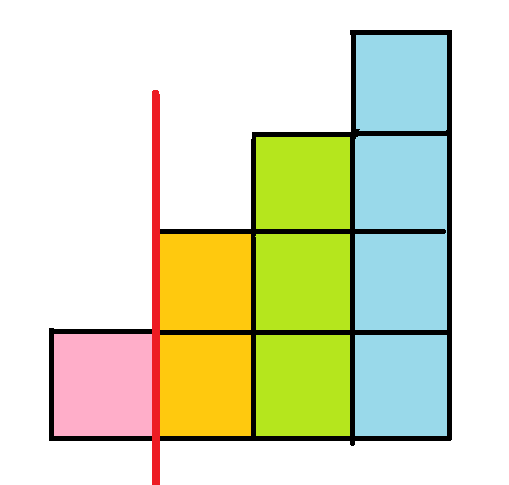
前綴和
子字串
用前綴和的方式
再除(or乘)上一個\(p\)的冪次使得每個子字串第一個字元乘的數是固定的
舉例: 問[1,3]和[0,2]是否一樣,[1,3]是誰?
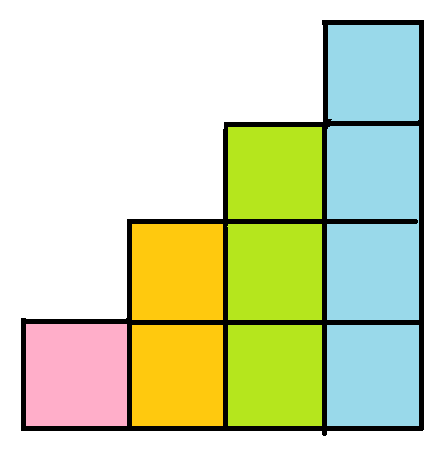
前綴和
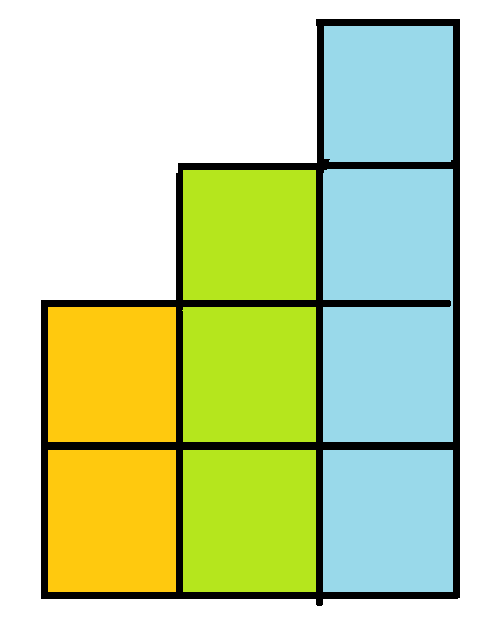
子字串
用前綴和的方式
再除(or乘)上一個\(p\)的冪次使得每個子字串第一個字元乘的數是固定的
舉例: 問[1,3]和[0,2]是否一樣,[1,3]是誰?
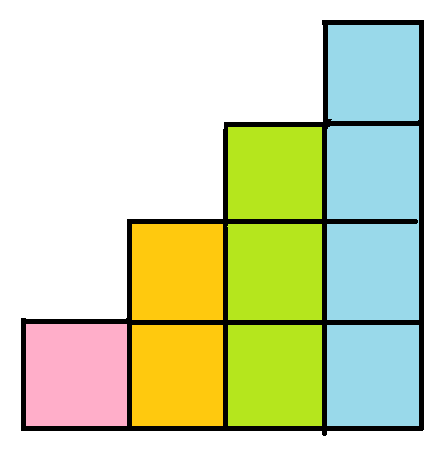
前綴和
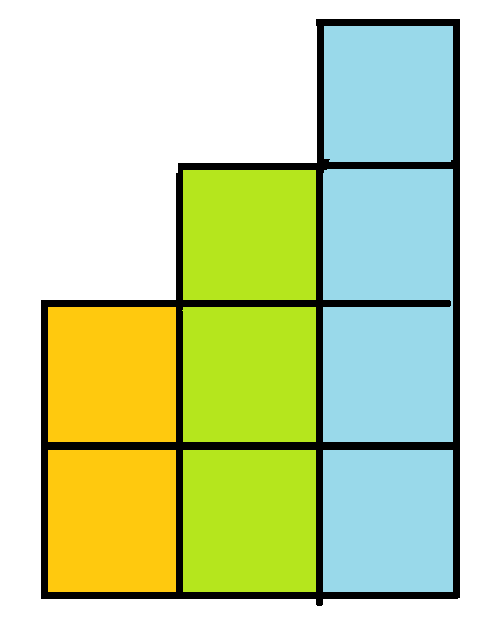
除冪次
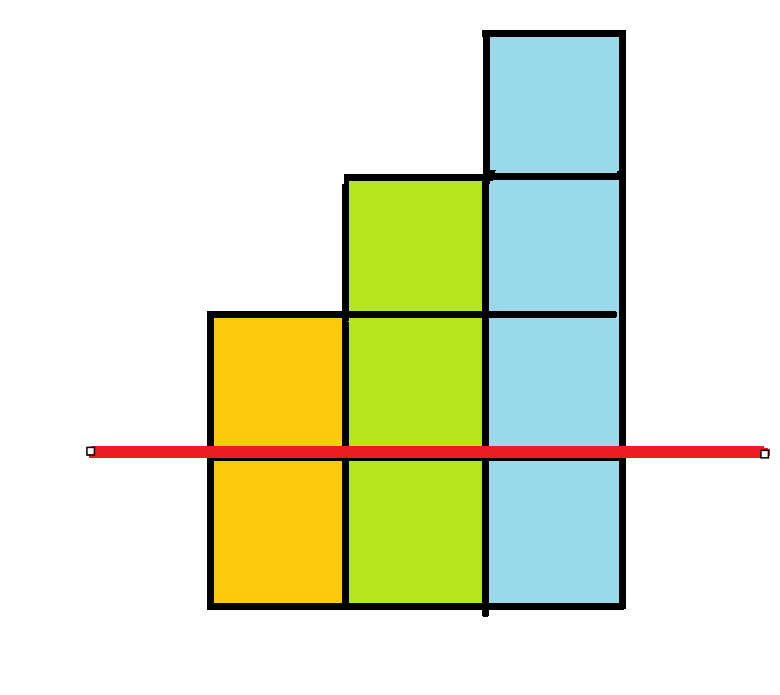
子字串
用前綴和的方式
再除(or乘)上一個\(p\)的冪次使得每個子字串第一個字元乘的數是固定的
舉例: 問[1,3]和[0,2]是否一樣,[1,3]是誰?
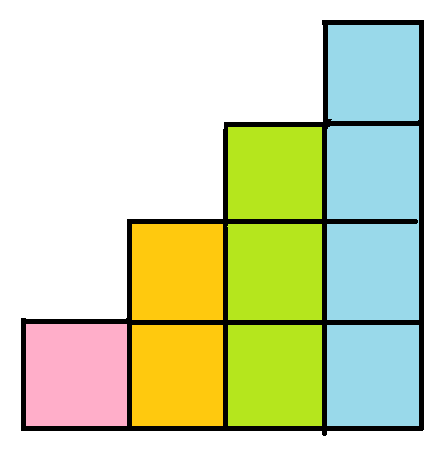
前綴和
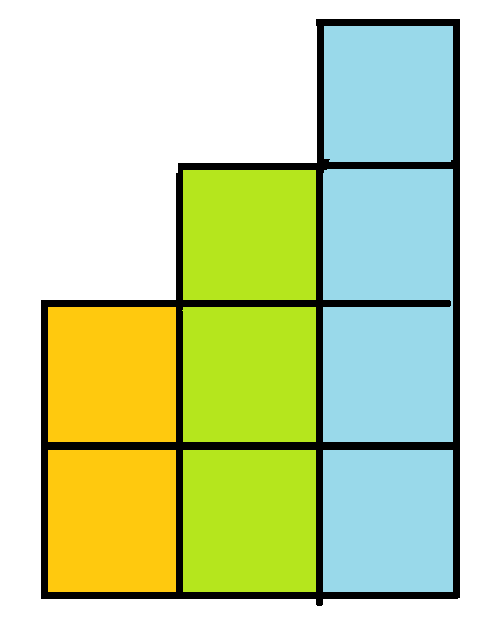
除冪次
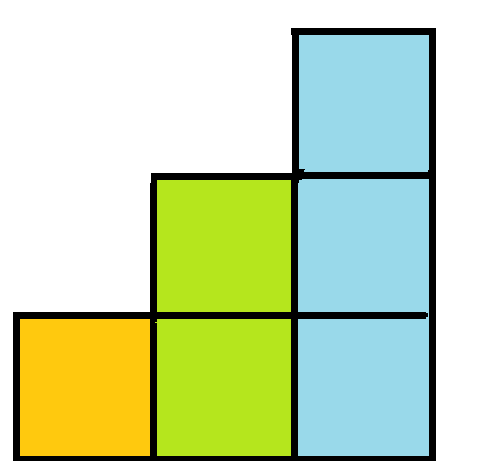
發生碰撞怎麼辦
碰撞的機率可以用生日悖論概算
會發現\(M\)(下面公式的\(N\))越大(值域越大),越難碰撞
所以就把\(M\)調大一點

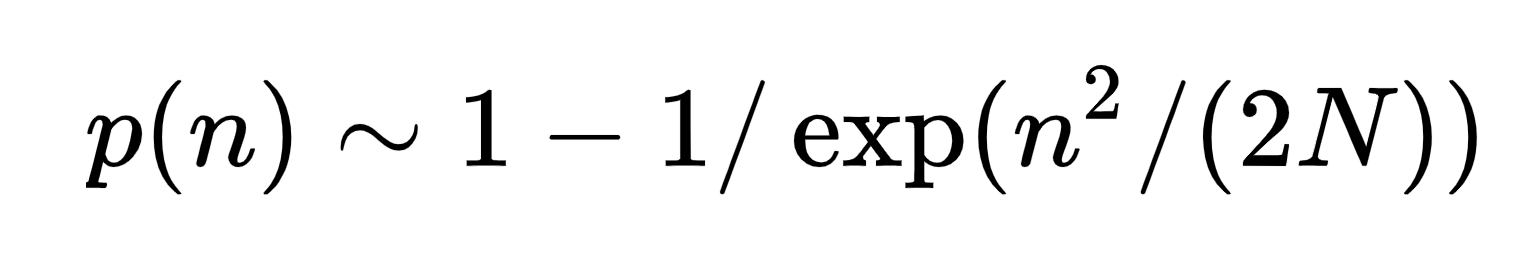
還是碰撞呢?
\(n = 0.83\sqrt{M}\)時,便約50%機率會碰撞了
還是碰撞呢?
一個便當不夠,就吃兩個
一個hash不夠,就用兩個
用兩組不同的\(p和M\),hash值用pair表示
$$值域從M變成M_1 M_2$$
參考code
//判斷兩個子字串是否一樣
#include <bits/stdc++.h>
using namespace std;
const int M=8e7+23, P=31;
long long pp[1010000];
int n, pre[1010000], q;
string s;
int f(int l, int r){
int res = pre[r];
if(l-1>=0) res-=pre[l-1];
res=(res+M)%M;
res=res*pp[n-l]%M; //把子字串第一個字元乘的p^(l-1)變成p^n
return res;
}
int main(){
pp[0]=1;
for(int i=1; i<1000010; i++) pp[i] = pp[i-1]*P%M;
cin >> n >> s;
for(int i=0; i<n; i++){
pre[i] = ( pre[i]+(s[i]-'a'+1)*pp[i] )%M;
pre[i+1]=pre[i];
}
cin >> q;
while(q--){
int l1, r1, l2, r2;
cin >> l1 >> r1 >> l2 >> r2;
if(f(l1,r1)==f(l2,r2)) cout << "Same!\n";
else cout << "qq!\n";
}
return 0;}習題
Trie
中文叫字典樹
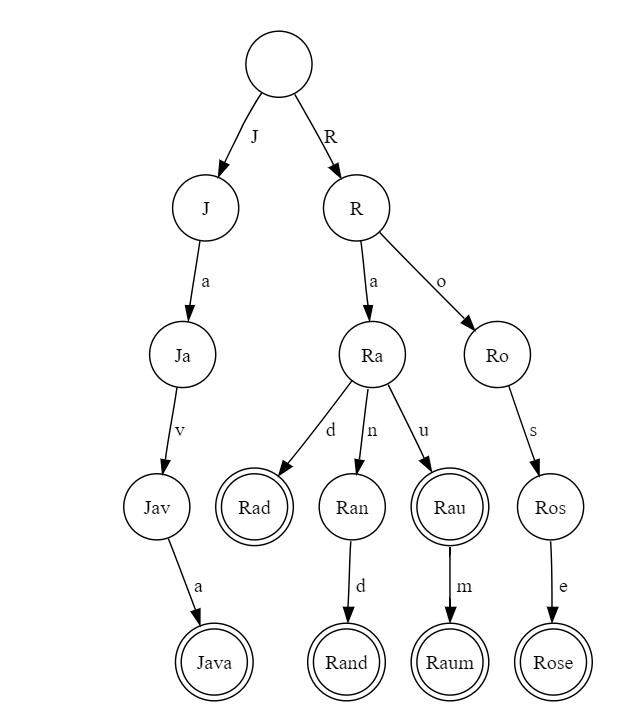
就是把很多字串用樹的結構存起來
右圖就是把Rad, Rau, Rand, Raum, Rose, Java放在樹上
$$有長度為n(<5000)的字串t和k個總長小於 10^6 的字串 s_1,s_2,...,s_k$$
$$問有幾種組合方式用s裡面的字串組出t$$
直接DP看看
$$設dp[0]=1$$
$$看到t的第i個字元的時候,看過所有s,如果 s_j可以i-1這個位置開始接$$
則從\(i-1\)轉移到 \( i-1+|s_j| \)
時間複雜度\(O(n*(s的總長))\),會TLE
放到Trie上
枚舉i,從\(t_i\)開始在Trie上走路,發現這個節點是\(s\)中的字串就轉移
每個i最多跟著走到n,所以時間複雜度\(O(n^2)\)
| dp | 1 | 0 | 0 | 0 | 0 | 0 |
|---|
a
b
a
b
c
a
c
b
b
a
b
| dp | 1 | 0 | 0 | 0 | 0 | 0 |
|---|
a
b
a
b
c
a
c
b
b
a
b
| dp | 1 | 0 | 1 | 0 | 0 | 0 |
|---|
a
b
a
b
c
a
c
b
b
a
b
| dp | 1 | 0 | 1 | 0 | 0 | 0 |
|---|
a
b
a
b
c
a
c
b
b
a
b
| dp | 1 | 0 | 1 | 0 | 1 | 0 |
|---|
a
b
a
b
c
a
c
b
b
a
b
| dp | 1 | 0 | 1 | 0 | 1 | 0 |
|---|
a
b
a
b
c
a
c
b
b
a
b
沒辦法繼續在Trie上跑
| dp | 1 | 0 | 1 | 0 | 1 | 0 |
|---|
a
b
a
b
c
a
c
b
b
a
b
b沒辦法在Trie上跑...
| dp | 1 | 0 | 1 | 0 | 1 | 0 |
|---|
a
b
a
b
c
a
c
b
b
a
b
| dp | 1 | 0 | 1 | 0 | 2 | 0 |
|---|
a
b
a
b
c
a
c
b
b
a
b
| dp | 1 | 0 | 1 | 0 | 2 | 0 |
|---|
a
b
a
b
c
a
c
b
b
a
b
沒辦法繼續在Trie上跑
| dp | 1 | 0 | 1 | 0 | 2 | 0 |
|---|
a
b
a
b
c
a
c
b
b
a
b
b沒辦法在Trie上跑...
| dp | 1 | 0 | 1 | 0 | 2 | 2 |
|---|
a
b
a
b
c
a
c
b
b
a
b
| dp | 1 | 0 | 1 | 0 | 2 | 2 |
|---|
a
b
a
b
c
a
c
b
b
a
b
已經是最後一個位元了,不用繼續跑了
答案就是2
Trie也很適合做位元操作,尤其是xor
給你一個長\(n(<10^5)\)的陣列\(a\),你可以隨便選個子陣列並得到所有元素xor起來的值
請找到能得到的最大值
可以先做前輟xor
然後就從看子陣列變成看兩個值
$$怎麼求\max_ {0 \le i,j \le n} a_i \oplus a_j ,其中a_0=0 $$
把二進位數字放到Trie上面,高位的靠近根節點
依序把數字放上去
放上去前看一下與已經放上去的數字xor的最大值
如果最高位可以選不一樣,那就選不一樣
放001上去得到答案為5
參考code
//假設有n個字串要放上Trie, 0是根節點
int m=0, nxt[1010000][26], cnt[1010000]={0}; //cnt[i]紀錄有幾個字串在i這個節點結束
for(int i=0; i<1000010; i++) for(int j=0; j<26; j++)nxt[i][j]=-1;
for(int i=0; i<n; i++){
string s;
cin>>s;
int now=0;
for(char c:s){
c-='a';
if(nxt[now][c]==-1) nxt[now][c]=++m;
now=nxt[now][c];}
cnt[now]++;
}習題
- 剛剛那兩題
- CF 1895D
- CF 37C
- CF 965E
- CF 655E
- luogu P7502
KMP
Knuth - Morris - Pratt Algorithm
有兩個字串t,s,問s在t中出現幾次
例:bb在bbabbb出現3次
這種問題叫做「字串匹配」,s叫模式字串,t叫主字串
暴力做很爛,\(O(|s||t|)\)
最大的困境在於下面這種case
t為一百萬個連續的a,s為十萬個連續的a接一個b
每次都配了十萬個a才發現這個b配不起來,又要重配
有沒有辦法可以重複利用已經配好的地方?
\(\pi\)函數

$$\pi[i]存的就是i前輟的「最長共同真前後輟」(次長共同前後輟)$$
這個函數又叫失配函數
也有人叫共同真前後綴border
\(\pi\)函數怎麼用
t為aabaabaaa,s為aabaaa
| a | a | b | a | a | a | |
|---|---|---|---|---|---|---|
| π | 1 | 0 | 1 | 2 | 2 |
\(\pi\)函數怎麼用
| a | a | b | a | a | a | |
|---|---|---|---|---|---|---|
| π | 1 | 0 | 1 | 2 | 2 |
aabaabaaa
aabaaa
配失敗了QQ
\(\pi\)函數怎麼用
| a | a | b | a | a | a | |
|---|---|---|---|---|---|---|
| π | 1 | 0 | 1 | 2 | 2 |
aabaabaaa
aabaaa
\(\pi\)函數怎麼用
| a | a | b | a | a | a | |
|---|---|---|---|---|---|---|
| π | 1 | 0 | 1 | 2 | 2 |
aabaabaaa
aabaaa
\(\pi\)函數怎麼用
| a | a | b | a | a | a | |
|---|---|---|---|---|---|---|
| π | 1 | 0 | 1 | 2 | 2 |
aabaabaaa
aabaaa
換個位置繼續配(不用從頭),這個位置是由\(\pi\)決定的
\(\pi\)函數怎麼用
| a | a | b | a | a | a | |
|---|---|---|---|---|---|---|
| π | 1 | 0 | 1 | 2 | 2 |
aabaabaaa
aabaaa
換個位置繼續配(不用從頭),這個位置是由\(\pi\)決定的
\(\pi\)函數怎麼求
暴力做比原本更爛
每個前綴\(|s|\)個要和自己的後綴(最多\(|s|\)個,最長長\(|s|\))比對
時間複雜度 \(O(|s|^3)\)
\(\pi\)函數怎麼求 - 觀察1
\( \pi[i+1] \leq \pi[i]+1 \)
簡易證明:
令\(\pi[i+1]=k\),則s[0 ~ k-1] = s[i+2-k ~ i+1]成立
顯然s[0 ~ k-2] = s[i+2-k ~ i]也成立
s[\(\pi\)[i]] = s[i+1]時,小於等於的等於才成立
\(\pi\)函數怎麼求 - 觀察2
那如果s[\(\pi\)[i]] != s[i+1] 呢?
"i+1前綴的最長共同真前後綴" 無法由 "i前綴的最長共同真前後綴" 推得
\(\pi\)函數怎麼求 - 觀察2
那如果s[\(\pi\)[i]] != s[i+1] 呢?
"i+1前綴的最長共同真前後綴" 無法由 "i前綴的最長共同真前後綴" 推得
ABCABB...ABCABC
\(\pi\)函數怎麼求 - 觀察2
那如果s[\(\pi\)[i]] != s[i+1] 呢?
"i+1前綴的最長共同真前後綴" 無法由 "i前綴的最長共同真前後綴" 推得
試圖由次長的推得
ABCABB...ABCABC
\(\pi\)函數怎麼求 - 觀察2
那如果s[\(\pi\)[i]] != s[i+1] 呢?
"i+1前綴的最長共同真前後綴" 無法由 "i前綴的最長共同真前後綴" 推得
試圖由次長的推得
ABCABB...ABCABC
次長的共同真前後綴
其實就是"最長共同真前後綴"的
最長共同真前後綴
\(\pi\)函數怎麼求 - 觀察2
那如果s[\(\pi\)[i]] != s[i+1] 呢?
"i+1前綴的最長共同真前後綴" 無法由 "i前綴的最長共同真前後綴" 推得
試圖由次長的推得
ABCABB...ABCABC
\(\pi\)函數怎麼求 - 觀察2
那如果s[\(\pi\)[i]] != s[i+1] 呢?
"i+1前綴的最長共同真前後綴" 無法由 "i前綴的最長共同真前後綴" 推得
試圖由次長的推得
ABCABB...ABCABC
\(\pi\)函數怎麼求 - 觀察2
那如果s[\(\pi\)[i]] != s[i+1] 呢?
"i+1前綴的最長共同真前後綴" 無法由 "i前綴的最長共同真前後綴" 推得
試圖由次長的推得
$$會發現次長的長度就是\pi[\pi[i]]$$
\(\pi\)函數怎麼求 - 觀察2
那如果s[\(\pi[i]\)] != s[i+1] 呢?
"i+1前綴的最長共同真前後綴" 無法由 "i前綴的最長共同真前後綴" 推得
試圖由次長的推得
$$會發現次長的長度就是\pi[\pi[i]-1]$$
次長還是配不到呢?
\(\pi\)函數怎麼求 - 觀察2
$$那如果s[\pi[i]] != s[i+1] 呢?$$
"i+1前綴的最長共同真前後綴" 無法由 "i前綴的最長共同真前後綴" 推得
試圖由次長的推得
$$會發現次長的長度就是\pi[\pi[i]-1]$$
次長還是配不到呢?
$$就再從第三長的配,也就是看s[\pi[\pi[\pi[i]-1]-1]]是不是等於s[i+1]$$
完整演算法
$$初始化\pi[0]=0$$
假設已經做完\(\pi[0\)~\(i]\)了
先令\(j=\pi[i]\)
$$看s[j]是否等於s[i+1],是就讓\pi[i+1]=j+1,否則讓j=\pi[j-1]$$
$$如果j=0還配失敗,那\pi[i+1]=0$$
時間複雜度
$$\pi最多增加|s|次(觀察一)$$
$$因為減少的一定\leq增加的(勢能),所以最多減少|s|次$$
$$時間複雜度O(|s|)$$
$$如果是s匹配t那\pi最多增加|t|次$$
$$時間複雜度O(|t|)$$
參考code
//CSES String Matching
#include <bits/stdc++.h>
using namespace std;
int n, m, pi[2100000];
string t, s;
int main(){
ios_base::sync_with_stdio(false); cin.tie(0);
cin >> t >> s;
n=t.size(), m=s.size();
pi[0]=0; int now=0; //匹配成功now個,要嘗試配s[now]和s[i]
for(int i=1; i<m; i++){
while(now>0 and s[i]!=s[now]) now=pi[now-1];
if(s[i]==s[now]) now++;
pi[i]=now;
}
int ans=0; now=0;
for(int i=0; i<n; i++){
while(now>0 and t[i]!=s[now]) now=pi[now-1];
if(t[i]==s[now]) now++;
if(now==m){
ans++;
now=pi[now-1];
}
}
cout << ans << '\n';
}
應用
$$如果一個前綴重複數次後,前|s|個字元組起來=s,則此前綴的長度是s的週期$$
$$該如何找到s的所有週期呢?$$
hash是一個辦法
但其實有非隨機性的算法
$$周期的另一個定義 : 若s[i]=s[i+p]對所有i\in[0,n-p-1]成立則p為s的週期$$
$$共同前後綴的定義 : 若s[i]=s[n-l+i]對所有i\in[0,l-1]成立則l前綴為s的共同前後綴$$
$$周期的另一個定義 : 若s[i]=s[i+p]對所有i\in[0,n-p-1]成立則p為s的週期$$
$$共同前後綴的定義 : 若s[i]=s[n-l+i]對所有i\in[0,l-1]成立則l前綴為s的共同前後綴$$
$$會發現每個共同求後綴(長l)都對應到字串的一個週期p=n-l$$
$$所以s的所有週期就是 n-\pi[n-1], n-\pi[\pi[n-1]-1]...$$
KMP自動機
也較做前綴自動機(Prefix Automaton)
有一個字串s,有q次詢問
$$每次詢問給你一個字串t,問s+t最後|t|個前綴的"最大共同前後綴"$$
- \(|s|\leq10^6\)
- \(q\leq10^5\)
- \(|t|\leq10\)
每次詢問都做一次KMP很燒雞
現在沒得均攤了(可能會+1然後-8)
$$可以開一個|s|\times26的二維陣列pa,pa[i][c]代表已匹配到長度i時,再匹配一個c時會匹到的長度$$
$$pa[i][c]可以從前面的pa得到$$
$$如果c=s[i],則pa[i][c]=i+1 (匹配成功繼續配下去)$$
$$否則pa[i][c]=pa[\pi[i-1]][c](匹配失敗)$$
$$\pi[i]也很好求了,\pi[i]就是pa[\pi[i-1]][s[i]]$$
abab
| a | b | a | b | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | ||||||
| pi[i] | 0 | ||||||||
| pa[i]['a'] | 1 | ||||||||
| pa[i]['b'] | 0 | ||||||||
| pa[i]['c'] | 0 |
s
abab
| a | b | a | b | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | ||||||
| pi[i] | 0 | 0 | |||||||
| pa[i]['a'] | 1 | ||||||||
| pa[i]['b'] | 0 | ||||||||
| pa[i]['c'] | 0 |
s
abab
| a | b | a | b | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | ||||||
| pi[i] | 0 | 0 | |||||||
| pa[i]['a'] | 1 | 1 | |||||||
| pa[i]['b'] | 0 | 2 | |||||||
| pa[i]['c'] | 0 | 0 |
s
abab
| a | b | a | b | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | ||||||
| pi[i] | 0 | 0 | 1 | ||||||
| pa[i]['a'] | 1 | 1 | |||||||
| pa[i]['b'] | 0 | 2 | |||||||
| pa[i]['c'] | 0 | 0 |
s
abab
| a | b | a | b | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | ||||||
| pi[i] | 0 | 0 | 1 | ||||||
| pa[i]['a'] | 1 | 1 | 3 | ||||||
| pa[i]['b'] | 0 | 2 | 0 | ||||||
| pa[i]['c'] | 0 | 0 | 0 |
s
abab
| a | b | a | b | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | ||||||
| pi[i] | 0 | 0 | 1 | 2 | |||||
| pa[i]['a'] | 1 | 1 | 3 | ||||||
| pa[i]['b'] | 0 | 2 | 0 | ||||||
| pa[i]['c'] | 0 | 0 | 0 |
s
abab
| a | b | a | b | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | ||||||
| pi[i] | 0 | 0 | 1 | 2 | |||||
| pa[i]['a'] | 1 | 1 | 3 | 1 | |||||
| pa[i]['b'] | 0 | 2 | 0 | 4 | |||||
| pa[i]['c'] | 0 | 0 | 0 | 0 |
s
abab
| a | b | a | b | a | |||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | |||||
| pi[i] | 0 | 0 | 1 | 2 | |||||
| pa[i]['a'] | 1 | 1 | 3 | 1 | |||||
| pa[i]['b'] | 0 | 2 | 0 | 4 | |||||
| pa[i]['c'] | 0 | 0 | 0 | 0 |
s
a
t
abab
| a | b | a | b | a | |||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | |||||
| pi[i] | 0 | 0 | 1 | 2 | 3 | ||||
| pa[i]['a'] | 1 | 1 | 3 | 1 | |||||
| pa[i]['b'] | 0 | 2 | 0 | 4 | |||||
| pa[i]['c'] | 0 | 0 | 0 | 0 |
s
a
t
可以用pa算pi
abab
| a | b | a | b | a | |||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | |||||
| pi[i] | 0 | 0 | 1 | 2 | 3 | ||||
| pa[i]['a'] | 1 | 1 | 3 | 1 | 3 | ||||
| pa[i]['b'] | 0 | 2 | 0 | 4 | |||||
| pa[i]['c'] | 0 | 0 | 0 | 0 |
s
a
t
配到a就可以繼續配下去
abab
| a | b | a | b | a | |||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | |||||
| pi[i] | 0 | 0 | 1 | 2 | 3 | ||||
| pa[i]['a'] | 1 | 1 | 3 | 1 | 3 | ||||
| pa[i]['b'] | 0 | 2 | 0 | 4 | 0 | ||||
| pa[i]['c'] | 0 | 0 | 0 | 0 |
s
a
t
配到b就死了重配
abab
| a | b | a | b | b | |||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | |||||
| pi[i] | 0 | 0 | 1 | 2 | 0 | ||||
| pa[i]['a'] | 1 | 1 | 3 | 1 | |||||
| pa[i]['b'] | 0 | 2 | 0 | 4 | |||||
| pa[i]['c'] | 0 | 0 | 0 | 0 |
s
b
t
可以用pa算pi
$$可以開一個|s|\times26的二維陣列pa,pa[i][c]代表已匹配到長度i時,再匹配一個c時會匹到的長度$$
$$這樣的話\pi[i]就很好求了,\pi[i]就是pa[\pi[i-1]][s[i]]$$
$$pa[i][c]也可以從前面的pa得到$$
$$如果c=s[i],則pa[i][c]=i+1$$
$$否則pa[i][c]=pa[\pi[i-1]][c]$$
$$對於這題,前面可以O(26|s|)解決,後面則可以O(26*q*10)解決$$
這個技巧叫做Prefix Automaton前綴自動機,又或是KMP自動機
習題
- 前面那兩題
- luogu p4391
- CF 808G
Aho-corasick automaton
中文習慣叫AC自動機
就是把kmp失配函數的概念丟到Trie上
會連很多fail link(失配邊),這個邊是從字串s指到s在Trie上的最長真後綴,
如果沒有任何後綴在Trie上就指向根。失配邊會組成一棵失配樹(若把邊反向)
可以同時對很多個字串匹配(多模式匹配)

註:上圖沒有紅邊的點的失配邊是指向根的
在trie上,深度和字串長度有關
每次跳失配邊,深度一定變小,所以沒有有向環
又跳著跳著,總是會跳到一個點連回根

失配邊一定做得出一棵反向的樹嗎
註:上圖沒有紅邊的點的失配邊是指向根的
可以看AC、ACG, CTGT, TG 在 ACTGTG各出現幾次
在Trie上走路,走不了就走走看失配邊
每走一步,就記下當前位置,沿著失配邊跑回根,沿途使經過的字串被算到。最後再瞬移回到原本的位置

怎麼用
註:上圖沒有紅邊的點的失配邊是指向根的

A C T G T G
0
0
0
0
0
0
0
0
0
0

A C T G T G
0
0
0
0
0
0
0
0
0
0


A C T G T G
0
0
0
0
0
0
0
0
0
0


A C T G T G
0
0
0
0
0
0
0
0
0
0


A C T G T G
0
0
0
0
0
0
0
0
0
0

跳跳跳跳


A C T G T G
0
1
0
0
0
0
0
0
0
0

跳跳跳跳


A C T G T G
1
1
0
0
0
0
0
0
0
0

跳跳跳跳


A C T G T G
1
1
0
0
0
0
0
0
0
0

完

A C T G T G
1
1
0
0
0
0
0
0
0
0


A C T G T G
1
1
0
0
0
0
0
0
0
0


A C T G T G
1
1
0
0
0
0
0
0
0
0

跳跳跳跳


A C T G T G
1
1
1
0
0
0
0
0
0
0

跳跳跳跳


A C T G T G
1
1
1
0
1
0
0
0
0
0

跳跳跳跳


A C T G T G
2
1
1
0
1
0
0
0
0
0

跳跳跳跳


A C T G T G
2
1
1
0
1
0
0
0
0
0

完

A C T G T G
2
1
1
0
1
0
0
0
0
0


A C T G T G
2
1
1
0
1
0
0
0
0
0

痾無路可走

A C T G T G
2
1
1
0
1
0
0
0
0
0

痾無路可走
失配邊!

A C T G T G
2
1
1
0
1
0
0
0
0
0

痾無路可走
失配邊!

A C T G T G
2
1
1
0
1
0
0
0
0
0


A C T G T G
2
1
1
0
1
0
0
0
0
0


A C T G T G
2
1
1
0
1
0
0
0
0
0

跳跳跳跳

A C T G T G
2
1
1
0
1
0
0
0
0
0

跳跳跳跳


A C T G T G
2
1
1
0
1
1
0
0
0
0

跳跳跳跳


A C T G T G
2
1
1
0
1
1
0
1
0
0

跳跳跳跳


A C T G T G
3
1
1
0
1
1
0
1
0
0

跳跳跳跳


A C T G T G
3
1
1
0
1
1
0
1
0
0

完

A C T G T G
3
1
1
0
1
1
0
1
0
0


A C T G T G
3
1
1
0
1
1
0
1
0
0


A C T G T G
3
1
1
0
1
1
0
1
0
0

跳跳跳跳


A C T G T G
3
1
1
0
1
1
1
1
0
0

跳跳跳跳


A C T G T G
3
1
1
0
1
1
1
1
1
0

跳跳跳跳


A C T G T G
3
1
1
0
1
1
1
1
1
0

跳跳跳跳


A C T G T G
4
1
1
0
1
1
1
1
1
0

跳跳跳跳


A C T G T G
4
1
1
0
1
1
1
1
1
0

完

A C T G T G
4
1
1
0
1
1
1
1
1
0


A C T G T G
4
1
1
0
1
1
1
1
1
0


A C T G T G
4
1
1
0
1
1
1
1
1
0

跳跳跳跳


A C T G T G
4
1
1
0
1
1
1
1
1
1

跳跳跳跳


A C T G T G
4
1
1
0
1
1
1
1
1
1

跳跳跳跳


A C T G T G
5
1
1
0
1
1
1
1
1
1

跳跳跳跳


A C T G T G
5
1
1
0
1
1
1
1
1
1

完

A C T G T G
5
1
1
0
1
1
1
1
1
1

痾無路可走
失配邊!

A C T G T G
5
1
1
0
1
1
1
1
1
1


A C T G T G
5
1
1
0
1
1
1
1
1
1


A C T G T G
5
1
1
0
1
1
1
1
1
1


A C T G T G
5
1
1
0
1
1
1
1
1
1

跳跳跳跳


A C T G T G
5
1
1
0
1
1
1
1
2
1

跳跳跳跳


A C T G T G
5
1
1
0
1
1
1
2
2
1

跳跳跳跳


A C T G T G
6
1
1
0
1
1
1
2
2
1

跳跳跳跳


A C T G T G
6
1
1
0
1
1
1
2
2
1


6
1
1
0
1
1
1
2
2
1
完
A C T G T G

A C T G T G
6
1
1
0
1
1
1
2
2
1
完
會發現每個點的標記就是他(子字串)出現的次數
如TG就確實是2次、CTG確實1次
不在trie上的如ACTG就不會知道有幾次
怎麼求
先建好Trie
用bfs的方式遍歷整顆Trie
怎麼求
考慮目前正在求u的失配邊,u和父節點p之間隔的是字元c
如果fail[p]有連c出去:
那就讓fail[u]=son[fail[p]][c]
怎麼求
考慮目前正在求u的失配邊,u和父節點p之間隔的是字元c
如果fail[p]有連c出去:
那就讓fail[u]=son[fail[p]][c]
怎麼求
考慮目前正在求u的失配邊,u和父節點p之間隔的是字元c
如果fail[p]有連c出去:
那就讓fail[u]=son[fail[p]][c]
怎麼求
考慮目前正在求u的失配邊,u和父節點p之間隔的是字元c
如果fail[p]有連c出去:
那就讓fail[u]=son[fail[p]][c]
怎麼求
考慮目前正在求u的失配邊,u和父節點p之間隔的是字元c
如果fail[p]沒有連c出去:
那就看看fail[fail[p]]有沒有連c出去,這樣一路跳到配到了或著遇到根還沒有
怎麼求
考慮目前正在求u的失配邊,u和父節點p之間隔的是字元c
如果fail[p]沒有連c出去:
那就看看fail[fail[p]]有沒有連c出去,這樣一路跳到配到了或著遇到根還沒有
怎麼求
考慮目前正在求u的失配邊,u和父節點p之間隔的是字元c
如果fail[p]沒有連c出去:
那就看看fail[fail[p]]有沒有連c出去,這樣一路跳到配到了或著遇到根還沒有
怎麼求
考慮目前正在求u的失配邊,u和父節點p之間隔的是字元c
如果fail[p]沒有連c出去:
那就看看fail[fail[p]]有沒有連c出去,這樣一路跳到配到了或著遇到根還沒有
我們跳回根了,發現可以連出去ㄟ!
怎麼求
考慮目前正在求u的失配邊,u和父節點p之間隔的是字元c
如果fail[p]沒有連c出去:
那就看看fail[fail[p]]有沒有連c出去,這樣一路跳到配到了或著遇到根還沒有
怎麼求
考慮目前正在求u的失配邊,u和父節點p之間隔的是字元c
如果fail[p]沒有連c出去:
那就看看fail[fail[p]]有沒有連c出去,這樣一路跳到配到了或著遇到根還沒有
怎麼求
考慮目前正在求u的失配邊,u和父節點p之間隔的是字元c
如果fail[p]沒有連c出去:
那就看看fail[fail[p]]有沒有連c出去,這樣一路跳到配到了或著遇到根還沒有
很像kmp吧
怎麼求
在建fail邊的時候,一路跳回去可能要8年(想想看aaaaaaaa這個鍊)
所以要做路徑壓縮
具體來說就是如果i連不出c這條邊,就設son[i][c]=son[fail[i]][c]
如果son[fail[i]]真的有連出c那很好,否則son[i][c]=son[fail[i]][c]=son[fail[fail[i]]][c]=...
這麼做在建失配邊的時就不用跳失配邊,無論fail[p]是否連c出去都直接fail[u]=son[fail[p]][c]
而在走路時也直接走到son[fail[p]][c]就好了
因為我不會講話所以放個參考閱讀
參考code
//0是根結點
#include <bits/stdc++.h>
using namespace std;
int n, cnt[1010000]={0}, fail[1010000]={0}, son[1010000][26]={0}, tn=0;
//n是模式字串數量,cnt是模式字串被匹配到的次數,fail是失配邊,son是trie上的樹邊,tn是trie的大小
vector<int> cs[1010000]; //這個node(trie上)有哪些字串
int main(){
//輸入、建trie
ios_base::sync_with_stdio(false); cin.tie(0);
cin >> n;
for(int i=1; i<=n; i++){
string s;
cin >> s;
int z=0;
for(char c:s){
c-='a';
if(!son[z][c])son[z][c]=++tn;
z=son[z][c];
}
cs[z].push_back(i);
}
string t; //主字串
cin >> t;
//建ac自動機
queue<int>q;
for(int i=0; i<26; i++) if(son[0][i]) q.push(son[0][i]); //直接從0開始的話,
while(q.size()){
int i=q.front(); q.pop();
for(int c=0; c<26; c++){
if(son[i][c]){
fail[son[i][c]] = son[fail[i]][c];
q.push(son[i][c]);
}
else son[i][c]=son[fail[i]][c]; //路徑壓縮
}
}
//ac自動機上面跑
int now=0;
for(char c:t){
now=son[now][c-'a'];
for(int j=now; j; j=fail[j]) for(int k:cs[j])cnt[k]++;
}
//輸出
for(int i=1; i<=n; i++)cout << cnt[i] << '\n';
}優化
雖然建自動機的複雜度是線性的
$$但匹配時每次都跑失配邊跑回根最壞複雜度蠻差的,O(|主字串|^2)$$
甚至比做很多次KMP還爛
例子 : 一百萬個連續的a中找a,aa,aaa,aaaa
優化
除了根節點以外,每個點都有(且只有一條)失配邊往上
將這些邊方向反過來且忽略trie的樹邊,這就成了一顆失配樹
在這顆失配樹上做樹DP,就不用每配個字元都跳一連串失配邊
$$時間複雜度變成O(26*模式字串總長+ |主字串|)$$
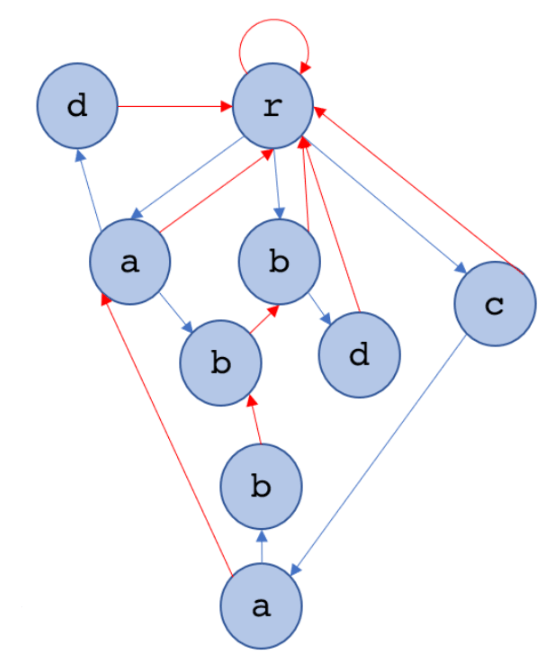
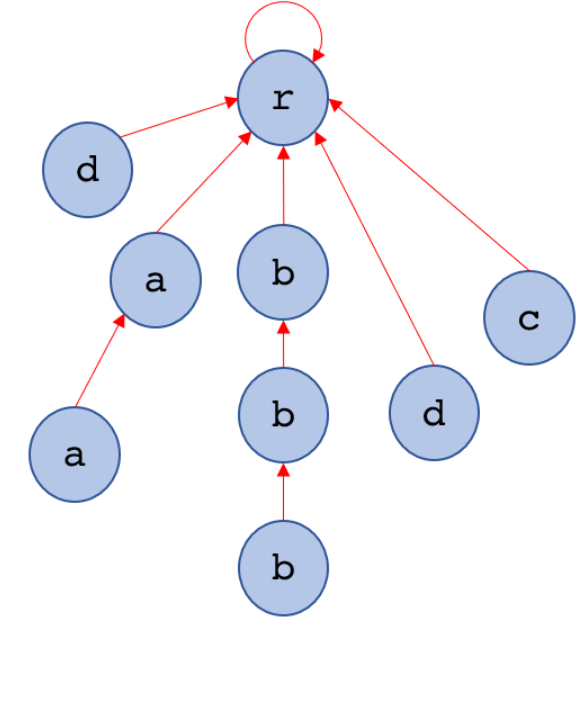
藍是Trie上的邊
優化
還有另一個優化叫last優化
另外存一個邊連到最長的後綴使得這個後綴也是一個模式字串
這個邊可以由失配邊得到
雖然複雜度不變,但據說這個優化能大幅優化常數
參考code 2
//可以過luogu P5357,原本的不行
#include <bits/stdc++.h>
using namespace std;
int n, ans[1010000]={0}, fail[1010000]={0}, son[1010000][26]={0}, tn=0;
//n是模式字串數量,ans是模式字串被匹配到的次數,fail是失配邊,son是trie上的樹邊,tn是trie的大小
vector<int> cs[1010000]; //這個node(trie上)有哪些字串
vector<int> fe[1010000]; //失配樹
int tmp[1010000]={0};
void dfs(int i){
for(int j:fe[i]){
dfs(j);
tmp[i]+=tmp[j];
}
for(int x:cs[i])ans[x]=tmp[i];
}
int main(){
//輸入、建trie
ios_base::sync_with_stdio(false); cin.tie(0);
cin >> n;
for(int i=1; i<=n; i++){
string s;
cin >> s;
int z=0;
for(char c:s){
c-='a';
if(!son[z][c])son[z][c]=++tn;
z=son[z][c];
}
cs[z].push_back(i);
}
string t; //主字串
cin >> t;
//建ac自動機
queue<int>q;
for(int i=0; i<26; i++) if(son[0][i]) q.push(son[0][i]);
while(q.size()){
int i=q.front(); q.pop();
for(int c=0; c<26; c++){
if(son[i][c]){
fail[son[i][c]] = son[fail[i]][c];
q.push(son[i][c]);
}
else son[i][c]=son[fail[i]][c]; //路徑壓縮
}
}
for(int i=1; i<=tn; i++) fe[fail[i]].push_back(i);
//ac自動機上面跑
int now=0;
for(char c:t){
now=son[now][c-'a'];
tmp[now]++;
}
//在失配樹上做DP
dfs(0);
//輸出
for(int i=1; i<=n; i++)cout << ans[i] << '\n';
}習題
- TIOJ 1306(裸,卡記憶體,dsu存重複字串)
- luogu P5357(裸)
- TIOJ 2192 (CF 808G困難版)
Z
時間複雜度
$$l+z[l]只有在重配時才有機會增加(上面2.和1-2.)$$
$$其他狀況,l+z[l]會不變$$
$$所以均攤O(|s|)$$
題外話
其實Z和KMP可以互換
參考code
//CSES String Matching
#include <bits/stdc++.h>
using namespace std;
int n, z[2010000], ans=0;
int main(){
ios_base::sync_with_stdio(false);
string s, t;
cin >> s >> t;
s=t+"$"+s;
int l=0; z[0]=0;
for(int i=1; i<s.size(); i++){
if(i<l+z[l]){
z[i]=z[i-l];
if(i+z[i]>l+z[l])z[i]=l+z[l]-i;
}
else l=i;
while(i+z[i]<s.size() and s[z[i]]==s[i+z[i]])z[i]++; //如果i'+z[i'] < l+z[l] 則不會跑這行
if(i+z[i]>l+z[l])l=i;
if(z[i]==t.size())ans++; //找到了
}
cout << ans << '\n';
} 習題
- KMP能做的應該都能做,可能辛苦些,可能簡單些
- abc 343 g
Manacher
和Z有8成像
時間複雜度
和Z一模一樣的邏輯
$$l+m[l]只有在重配時有機會增加$$
$$其他狀況,l+m[l]會不變$$
$$所以均攤O(|s|)$$
參考code
//CSES Longest Palindrome
//我的m比簡報裡的多一
#include <bits/stdc++.h>
using namespace std;
int n, m[2010000], ans=0;
int main(){
ios_base::sync_with_stdio(false);
string s="*", os;
cin >> os;
for(char c:os)s+=c, s+="*";
int l=0; m[0]=1;
for(int i=1; i<s.size(); i++){
if(i<l+m[l]){
m[i]=m[l-(i-l)];
if(i+m[i]>l+m[l])m[i]=l+m[l]-i;
}
else l=i;
while(i+m[i]<s.size() and s[i-m[i]]==s[i+m[i]])m[i]++;
if(i+m[i]>l+m[l])l=i;
}
int mxid=max_element(m+1,m+s.size())-m;
for(int i=mxid-m[mxid]+1; i<mxid+m[mxid]; i++)if(s[i]!='*')cout << s[i];
cout << '\n';
return 0;}Suffix array
中文叫後綴數組
排序後綴
0 aabbab$
1 abbab$
2 bbab$
3 bab$
4 ab$
5 b$
6 $6 $
0 aabbab$
4 ab$
1 abbab$
5 b$
3 bab$
2 bbab$排序
在這,6 0 4 1 5 3 2是我們想要得到的答案
暴力做
$$列出所有的(|S|個)後綴$$
然後直接用內建排序
$$時間複雜度O({|S|}^2 log |S|)$$
暴力做
vector<int> SA(string s) {
int n = s.size();
vector<int> sa(n + 1);
vector<pair<string, int>> v(n + 1);
for (int i = 0; i <= n; i++) v[i] = {s.substr(i, n - i), i};
sort(v.begin(), v.end());
for (int i = 0; i <= n; i++) sa[i] = v[i].second;
return sa;
}優化
暴力解很爛,要想個優化
我們可以試著用類似倍增的方式
先對前1位排序再對前2位排序再對前4位排序...
存字串的另一種方式
字串加上'$',接著把所有的後綴改成cycle
存字串的另一種方式
字串加上'$',接著把所有的後綴改成cycle
0 aabbab$
1 abbab$
2 bbab$
3 bab$
4 ab$
5 b$
6 $6 $
0 aabbab$
4 ab$
1 abbab$
5 b$
3 bab$
2 bbab$排序
存字串的另一種方式
字串加上'$',接著把所有的後綴改成cycle
因為'$'比'a'~'z'都還小,所以排序結果不變
這樣比較方便做我們等下要做的事
然後只要記是第幾後綴就知道長怎樣
0 aabbab$
1 abbab$a
2 bbab$aa
3 bab$aab
4 ab$aabb
5 b$aabba
6 $aabbab6 $aabbab
0 aabbab$
4 ab$aabb
1 abbab$a
5 b$aabba
3 bab$aab
2 bbab$aa排序
看動畫!
| Cyc | string | rank |
|---|---|---|
| 0 | aabbab$ | |
| 1 | abbab$a | |
| 2 | bbab$aa | |
| 3 | bab$aab | |
| 4 | ab$aabb | |
| 5 | b$aabba | |
| 6 | $aabbab |
#越偷越爽
先排第1個字元
#越偷越爽
\(_0a\)
\(_4a\)
\(_2b\)
\(_1a\)
\(_3b\)
\(_6\$\)
\(_5b\)
先排第1個字元
| Cyc | string | rank |
|---|---|---|
| 0 | aabbab$ | |
| 1 | abbab$a | |
| 2 | bbab$aa | |
| 3 | bab$aab | |
| 4 | ab$aabb | |
| 5 | b$aabba | |
| 6 | $aabbab |
#越偷越爽
\(_0a\)
\(_4a\)
\(_2b\)
\(_1a\)
\(_3b\)
\(_6\$\)
\(_5b\)
先排第1個字元
| Cyc | string | rank |
|---|---|---|
| 0 | aabbab$ | |
| 1 | abbab$a | |
| 2 | bbab$aa | |
| 3 | bab$aab | |
| 4 | ab$aabb | |
| 5 | b$aabba | |
| 6 | $aabbab |
#越偷越爽
\(_0a\)
1
\(_4a\)
1
\(_2b\)
4
\(_1a\)
1
\(_3b\)
4
\(_6\$\)
0
\(_5b\)
4
先排第1個字元
| Cyc | string | rank |
|---|---|---|
| 0 | aabbab$ | |
| 1 | abbab$a | |
| 2 | bbab$aa | |
| 3 | bab$aab | |
| 4 | ab$aabb | |
| 5 | b$aabba | |
| 6 | $aabbab |
#越偷越爽
\(_0a\)
1
\(_4a\)
1
\(_2b\)
4
\(_1a\)
1
\(_3b\)
4
\(_6\$\)
0
\(_5b\)
4
排好第一個字元了
| Cyc | string | rank |
|---|---|---|
| 0 | aabbab$ | 1 |
| 1 | abbab$a | 1 |
| 2 | bbab$aa | 4 |
| 3 | bab$aab | 4 |
| 4 | ab$aabb | 1 |
| 5 | b$aabba | 4 |
| 6 | $aabbab | 0 |
#越偷越爽
\(_0a _1a\)
1,?
\(_4a _5b\)
1,?
\(_2b _3b\)
4,?
\(_1a _2b\)
1,?
\(_3b _4a\)
4,?
\(_6\$ _0a\)
0,?
\(_5b _6\$\)
4,?
把第一個和第二個字元換成一對rank
| Cyc | string | rank |
|---|---|---|
| 0 | aabbab$ | 1 |
| 1 | abbab$a | 1 |
| 2 | bbab$aa | 4 |
| 3 | bab$aab | 4 |
| 4 | ab$aabb | 1 |
| 5 | b$aabba | 4 |
| 6 | $aabbab | 0 |
#越偷越爽
\(_0a _1a\)
1,?
\(_4a\) \( _5b\)
1,?
\(_2b _3b\)
4,?
\(_1a _2b\)
1,?
\(_3b _4a\)
4,?
\(_6\$ _0a\)
0,?
\(_5b _6\$\)
4,?
把第一個和第二個字元換成一對rank
| Cyc | string | rank |
|---|---|---|
| 0 | aabbab$ | 1 |
| 1 | abbab$a | 1 |
| 2 | bbab$aa | 4 |
| 3 | bab$aab | 4 |
| 4 | ab$aabb | 1 |
| 5 | b$aabba | 4 |
| 6 | $aabbab | 0 |
隨便抓個例子
#越偷越爽
\(_0a _1a\)
1,?
\(_4a\) \( _5b\)
1,?
\(_2b _3b\)
4,?
\(_1a _2b\)
1,?
\(_3b _4a\)
4,?
\(_6\$ _0a\)
0,?
\(_5b _6\$\)
4,?
把第一個和第二個字元換成一對rank
| Cyc | string | rank |
|---|---|---|
| 0 | aabbab$ | 1 |
| 1 | abbab$a | 1 |
| 2 | bbab$aa | 4 |
| 3 | bab$aab | 4 |
| 4 | ab$aabb | 1 |
| 5 | b$aabba | 4 |
| 6 | $aabbab | 0 |
隨便抓個例子
#越偷越爽
\(_0a _1a\)
1,?
\(_4a\) \( _5b\)
1,4
\(_2b _3b\)
4,?
\(_1a _2b\)
1,?
\(_3b _4a\)
4,?
\(_6\$ _0a\)
0,?
\(_5b _6\$\)
4,?
把第一個和第二個字元換成一對rank
| Cyc | string | rank |
|---|---|---|
| 0 | aabbab$ | 1 |
| 1 | abbab$a | 1 |
| 2 | bbab$aa | 4 |
| 3 | bab$aab | 4 |
| 4 | ab$aabb | 1 |
| 5 | b$aabba | 4 |
| 6 | $aabbab | 0 |
隨便抓個例子
#越偷越爽
\(_0a _1a\)
1,1
\(_4a _5b\)
1,4
\(_2b _3b\)
4,4
\(_1a _2b\)
1,4
\(_3b _4a\)
4,1
\(_6\$ _0a\)
0,1
\(_5b _6\$\)
4,0
把第一個和第二個字元換成一對rank
換完要重新排序
| Cyc | string | rank |
|---|---|---|
| 0 | aabbab$ | 1 |
| 1 | abbab$a | 1 |
| 2 | bbab$aa | 4 |
| 3 | bab$aab | 4 |
| 4 | ab$aabb | 1 |
| 5 | b$aabba | 4 |
| 6 | $aabbab | 0 |
#越偷越爽
接下來要把一對rank變一個新的rank(重新編號)
\(_0a _1a\)
1,1
\(_4a _5b\)
1,4
\(_2b _3b\)
4,4
\(_1a _2b\)
1,4
\(_3b _4a\)
4,1
\(_6\$ _0a\)
0,1
\(_5b _6\$\)
4,0
| Cyc | string | rank |
|---|---|---|
| 0 | aabbab$ | 1 |
| 1 | abbab$a | 1 |
| 2 | bbab$aa | 4 |
| 3 | bab$aab | 4 |
| 4 | ab$aabb | 1 |
| 5 | b$aabba | 4 |
| 6 | $aabbab | 0 |
#越偷越爽
\(_0a _1a\)
1
\(_4a _5b\)
2
\(_1a _2b\)
2
\(_6\$ _0a\)
0
再把rank更新上去
\(_2b _3b\)
6
\(_3b _4a\)
5
\(_5b _6\$\)
4
| Cyc | string | rank |
|---|---|---|
| 0 | aabbab$ | 1 |
| 1 | abbab$a | 1 |
| 2 | bbab$aa | 4 |
| 3 | bab$aab | 4 |
| 4 | ab$aabb | 1 |
| 5 | b$aabba | 4 |
| 6 | $aabbab | 0 |
#越偷越爽
前兩個字元就排完了
| Cyc | string | rank |
|---|---|---|
| 0 | aabbab$ | 1 |
| 1 | abbab$a | 2 |
| 2 | bbab$aa | 6 |
| 3 | bab$aab | 5 |
| 4 | ab$aabb | 2 |
| 5 | b$aabba | 4 |
| 6 | $aabbab | 0 |
\(_0a _1a\)
1
\(_4a _5b\)
2
\(_1a _2b\)
2
\(_6\$ _0a\)
0
\(_2b _3b\)
6
\(_3b _4a\)
5
\(_5b _6\$\)
4
#越偷越爽
接下來就是把前四個排好
| Cyc | string | rank |
|---|---|---|
| 0 | aabbab$ | 1 |
| 1 | abbab$a | 2 |
| 2 | bbab$aa | 6 |
| 3 | bab$aab | 5 |
| 4 | ab$aabb | 2 |
| 5 | b$aabba | 4 |
| 6 | $aabbab | 0 |
\(_0a a _2bb\)
1,?
\(_4ab _6\$a\)
2,?
\(_1ab _3ba\)
2,?
\(_6\$a _1ab\)
0,?
\(_2bb _4ab\)
6,?
\(_3ba _5b\$\)
5,?
\(_5b\$ _0aa\)
4,?
#越偷越爽
把一對rank變一個新的rank(重新編號)
| Cyc | string | rank |
|---|---|---|
| 0 | aabbab$ | 1 |
| 1 | abbab$a | 2 |
| 2 | bbab$aa | 6 |
| 3 | bab$aab | 5 |
| 4 | ab$aabb | 2 |
| 5 | b$aabba | 4 |
| 6 | $aabbab | 0 |
\(_0a a _2bb\)
1,6
\(_4ab _6\$a\)
2,0
\(_1ab _3ba\)
2,5
\(_6\$a _1ab\)
0,2
\(_2bb _4ab\)
6,2
\(_3ba _5b\$\)
5,4
\(_5b\$ _0aa\)
4,0
#越偷越爽
接下來更新rank
| Cyc | string | rank |
|---|---|---|
| 0 | aabbab$ | 1 |
| 1 | abbab$a | 2 |
| 2 | bbab$aa | 6 |
| 3 | bab$aab | 5 |
| 4 | ab$aabb | 2 |
| 5 | b$aabba | 4 |
| 6 | $aabbab | 0 |
\(_0a a _2bb\)
1
\(_4ab _6\$a\)
2
\(_1ab _3ba\)
3
\(_6\$a _1ab\)
0
\(_2bb _4ab\)
6
\(_3ba _5b\$\)
5
\(_5b\$ _0aa\)
4
#越偷越爽
這樣就排完4個字元了
| Cyc | string | rank |
|---|---|---|
| 0 | aabbab$ | 1 |
| 1 | abbab$a | 3 |
| 2 | bbab$aa | 6 |
| 3 | bab$aab | 5 |
| 4 | ab$aabb | 2 |
| 5 | b$aabba | 4 |
| 6 | $aabbab | 0 |
\(_0a a _2bb\)
1
\(_4ab _6\$a\)
2
\(_1ab _3ba\)
3
\(_6\$a _1ab\)
0
\(_2bb _4ab\)
6
\(_3ba _5b\$\)
5
\(_5b\$ _0aa\)
4
#越偷越爽
接下來還要再做最後一次,然後多餘的字元沒差
然後接下來的動畫我不做了
| Cyc | string | rank |
|---|---|---|
| 0 | aabbab$ | 1 |
| 1 | abbab$a | 3 |
| 2 | bbab$aa | 6 |
| 3 | bab$aab | 5 |
| 4 | ab$aabb | 2 |
| 5 | b$aabba | 4 |
| 6 | $aabbab | 0 |
\(_0aabb _4ab\$a\)
1,?
\(_4ab\$a _1abba\)
2,?
\(_1abba _5b\$aa\)
3,?
\(_6\$aab _3bab\$\)
0,?
\(_2bbab _6\$aab\)
6,?
\(_3bab\$ _0aabb\)
5,?
\(_5b\$aa _2bbab\)
4,?
時間複雜度
$$分log |S|次$$
$$每次排序|S|個pair或字元,O(|S| log|S|)$$
$$總複雜度O(|S| {log}^2 |S|)$$
更好的時間複雜度
$$你知道嗎,這個排序演算法只要O(n)就能排好n個東西喔$$
$$雖然我不是數學家,但這聽起來很不錯對吧?$$
更好的時間複雜度
$$你知道嗎,這個排序演算法只要O(n)就能排好n個東西喔$$
$$雖然我不是數學家,但這聽起來很不錯對吧?$$
沒錯,radix sort和counting sort都是\(O(n)\)
但不常用的原因是他們的常數會隨著值域暴漲
不過在算SA的過程中,值域最多到\(|S|\),所以可用
$$O(|S|{log}^2|S|)變O(|S|log|S|)$$
參考code(沒加radix sort)
//cf edu step1 pA
#include <bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
#define fs first
#define sc second
#define P pair<pii,int>
void getrank(vector<P>&v, vector<int>&rk){
for(int i=0, j=0; i<v.size(); i=j){
while(j<v.size() and v[i].fs==v[j].fs)j++;
for(int k=i; k<j; k++)rk[v[k].sc]=i, v[k].fs.fs=i;
}
return;}
int main(){
ios_base::sync_with_stdio(false); cin.tie(0);
string s;
cin >> s;
s+='$';
int n=s.size();
vector<int>rk(n); vector<P>v(n);
for(int i=0; i<n; i++)v[i]={{s[i],0},i};
for(int k=0; (1<<k)<=n*2; k++){
sort(v.begin(),v.end());
getrank(v,rk);
for(int i=0; i<n; i++)v[i].fs.sc=rk[(v[i].sc+(1<<k))%n];
}
for(int i=0; i<n; i++)cout << v[i].sc << ' ';
cout << '\n';
}Suffix array應用
所以這可以幹嘛
每個子字串都是S的某個後綴的前綴
所以可以在SA上二分搜,然後看中間的後綴的前綴是不是等於t
如果發現中間的後綴太大(小)就更新右(左)界
$$時間複雜度O(|t| log |S|)$$
同理也可以做到字串匹配,也是同個複雜度
LCP
LCP是Longest Common Prefix的簡稱,通常記長度
ababac和abac的LCP是3
$$通常LCP(i,j)代表問S的sa[i]後綴和sa[j]後綴的LCP$$
LCP
顯然地有
$$LCP(i,j) = LCP(j,i)$$
$$LCP(i,i) = |sa[i]|$$
LCP
顯然地還有
$$LCP(i,j) = min(LCP(i,k), LCP(k,j)) ,其中i\le k\le j$$
進而得到
$$LCP(i,j) = min(LCP(i,i+1), LCP(i+1,i+2), ..., LCP(j-1,j))$$

LCP
所以只要知道LCP(0,1), LCP(1,2), LCP(2,3)... ,然後再用資料結構維護,就可以求任意LCP(i,j)了
怎麼找LCP(0,1), LCP(1,2), LCP(2,3)... ? (這些東西又稱LCP array)
LCP
怎麼算LCP array?
從0後綴、1後綴開始做,假設已算完LCP(rk[i]-1,rk[i]),要算LCP(rk[i+1]-1,rk[i+1])
i後綴丟掉最前面(變成i+1後綴)、sa[rk[i]]後綴丟掉最前面,則LCP會減一
LCP(rk[i+1],rk[sa[rk[i]+1]+1]) = LCP(rk[i],rk[i]+1)-1
LCP
怎麼算LCP array?
從0後綴、1後綴開始做,算LCP(rk[i]-1,rk[i])
sa[rk[i]-1]後綴丟掉最前面、sa[rk[i]]後綴丟掉最前面,則LCP會減一
LCP(rk[i+1],rk[sa[rk[i]+1]+1]) = LCP(rk[i],rk[i]+1)-1
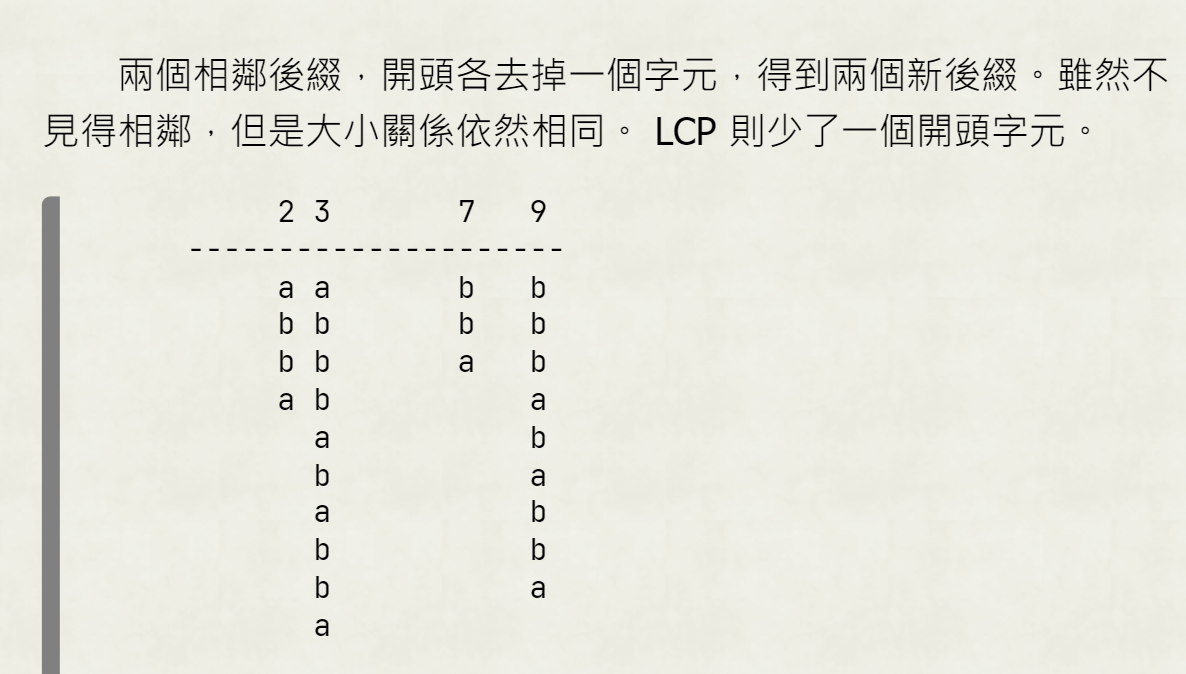
LCP
怎麼算LCP array?
從0後綴、1後綴開始做,算LCP(rk[i]-1,rk[i])
sa[rk[i]-1]後綴丟掉最前面、sa[rk[i]]後綴丟掉最前面,則LCP會減一
LCP(rk[i+1],rk[sa[rk[i]+1]+1]) = LCP(rk[i],rk[i]+1)-1

LCP
怎麼算LCP array?
從0後綴、1後綴開始做,算LCP(rk[i]-1,rk[i])
sa[rk[i]-1]後綴丟掉最前面、sa[rk[i]]後綴丟掉最前面,則LCP會減一
LCP(rk[i+1],rk[sa[rk[i]+1]+1]) = LCP(rk[i],rk[i]+1)-1

那9後綴和?後綴
的lcp是多少
LCP
怎麼算LCP array?
從0後綴、1後綴開始做,算LCP(rk[i]-1,rk[i])
sa[rk[i]-1]後綴丟掉最前面、sa[rk[i]]後綴丟掉最前面,則LCP會減一
LCP(rk[i+1],rk[sa[rk[i]+1]+1]) = LCP(rk[i],rk[i]+1)-1

那9後綴和?後綴
的lcp是多少
lcp結合起來是個min的關係,所以一定>=2
LCP
怎麼算LCP array?
從0後綴、1後綴開始做,算LCP(rk[i]-1,rk[i])
sa[rk[i]-1]後綴丟掉最前面、sa[rk[i]]後綴丟掉最前面,則LCP會減一
LCP(rk[i+1],rk[sa[rk[i]+1]+1]) = LCP(rk[i],rk[i]+1)-1

那9後綴和?後綴
的lcp是多少
lcp結合起來是個min的關係,所以一定>=2
當然7後綴和?也>=2
但我們不在乎
LCP
怎麼算LCP array?
從0後綴、1後綴開始做,假設已算完算LCP(rk[i]-1,rk[i]),要算LCP(rk[i+1]-1,rk[i+1])
i後綴丟掉最前面(變成i+1後綴)、sa[rk[i]]後綴丟掉最前面,則LCP會減一
一直扣掉最前面的字元(配到的長度減一),然後嘗試重配(可能加很多)
$$時間複雜度均攤O(|S|)$$
我懶得做動畫了(自CF EDU),然後Code、code2(演算法筆記)
我不會說話
- 對不起,我表達能力很糟糕
- 沒聽懂的推薦看 CF EDU,SAM571128的blog 也還不錯
習題
- CF EDU(後3step),記得要用O(n)sort
- TIOJ 2155
自己找,網路上很多
SAM(山姆)
後綴自動機

↖顏子喬
沒,我沒學,我只是嘴砲,我還要考期中考
Lyndon factorization
還沒做簡報
#include <bits/stdc++.h>
using namespace std;
string s;
int n;
int main() {
// ios_base::sync_with_stdio(false); cin.tie(0);
cin >> s;
n = s.size();
s = "0"+s;
int i = 1, ans = 0;
while (i <= n) {
// [1,i-1]做完了 [i,k-1]是almost-lyndon [j,k-1]是找找找段 [k,n]是待做段, j=k-|t|
int j = i, k = i + 1; // |t| = 1
while (k <= n) {
if (s[k] == s[j]) j++, k++; // |t|不變
else if (s[k] < s[j]) {
int len = k - j;
while (k - i >= len) {
i += len;
ans ^= (i-1);
}
break;
} // 這是一個新的almost-lyndon,把舊的重複段切出去
else j = i, k++; // almost-lyndon的重複段變成只有一個,也就是[i,k]
}
int len = k - j;
while (i <= j) {
i += len;
ans ^= (i-1);
}
}
cout << ans << '\n';
}回家學的東西
北市賽根本就不可能考
- 庫
- 回文自動機
- 後綴平衡樹
- SAM、SSAM
- Main-Lorentz Algorithm
- Boyer-Moore Algorithn
題目
- diao谷題庫(入門到入土)
我應該要列表說什麼可以甚麼解
但我還沒做
我不要換跟dp,我要換跟CSES
謝謝聆聽 抱歉浪費各位寶貴的三小時😣🙇🏽♂️
燒雞燒雞燒雞燒雞
Strings - 校培
By weakweakweak
Strings - 校培
- 521


