Learning From Corrupt Data
Sept 3, 2025
Adam Wei
Agenda
Sources of Robot Data
Open-X
expert robot teleop
robot teleop
simulation


Goal: sample "high-quality" trajectories for your task
Train on entire spectrum to learn "high-level" reasoning, semantics, etc
"corrupt"
"clean"
Types of "Corruption" in Robotics
- Sim2real gaps
- Task-level corruptions
- High-quality vs low-quality teleop data
- Change of low-level controller
- Embodiment gap
- Corruption in the conditioning variables
- ex. camera intrinsics/extrinsics, motion blur, etc
Research Questions

Giannis Daras

- How can we learn from both clean and corrupt data?
- Can these algorithms be adapted for robotics?
Project Outline
North Star Goal: Train with internet scale data (Open-X, AgiBot, etc)
Stepping Stone Experiments:
- Motion planning
- Sim-and-real co-training (planar pushing)
- Cross-embodied data (Lu's data)
- Bin picking
Algorithm Overview (w/o \(\sigma_{max}\))
Repeat:
- Sample (O, A, \(\sigma_{min}\)) ~ \(\mathcal{D}\)
- Choose noise level \(\sigma > \sigma_{min}\)
- Optimize denoiser or ambient loss
\(\sigma=1\)
\(\sigma=0\)
\(\sigma=\sigma_{min}\)
Corrupt Data (\(\sigma_{min}\geq0\))
Clean Data (\(\sigma_{min}=0\))
Loss Function (for \(x_0\sim q_0\))
\(\mathbb E[\lVert h_\theta(x_t, t) + \frac{\sigma_{min}^2\sqrt{1-\sigma_{t}^2}}{\sigma_t^2-\sigma_{min}^2}x_{t} - \frac{\sigma_{t}^2\sqrt{1-\sigma_{min}^2}}{\sigma_t^2-\sigma_{min}^2} x_{t_{min}} \rVert_2^2]\)
Ambient Loss
Denoising Loss
\(x_0\)-prediction
\(\epsilon\)-prediction
(assumes access to \(x_0\))
(assumes access to \(x_{t_{min}}\))
\(\mathbb E[\lVert h_\theta(x_t, t) - x_0 \rVert_2^2]\)
\(\mathbb E[\lVert h_\theta(x_t, t) - \epsilon \rVert_2^2]\)
\(\mathbb E[\lVert h_\theta(x_t, t) - \frac{\sigma_t^2 (1-\sigma_{min}^2)}{(\sigma_t^2 - \sigma_{min}^2)\sqrt{1-\sigma_t^2}}x_t + \frac{\sigma_t \sqrt{1-\sigma_t^2}\sqrt{1-\sigma_{min}^2}}{\sigma_t^2 - \sigma_{min}^2}x_{t_{min}}\rVert_2^2]\)
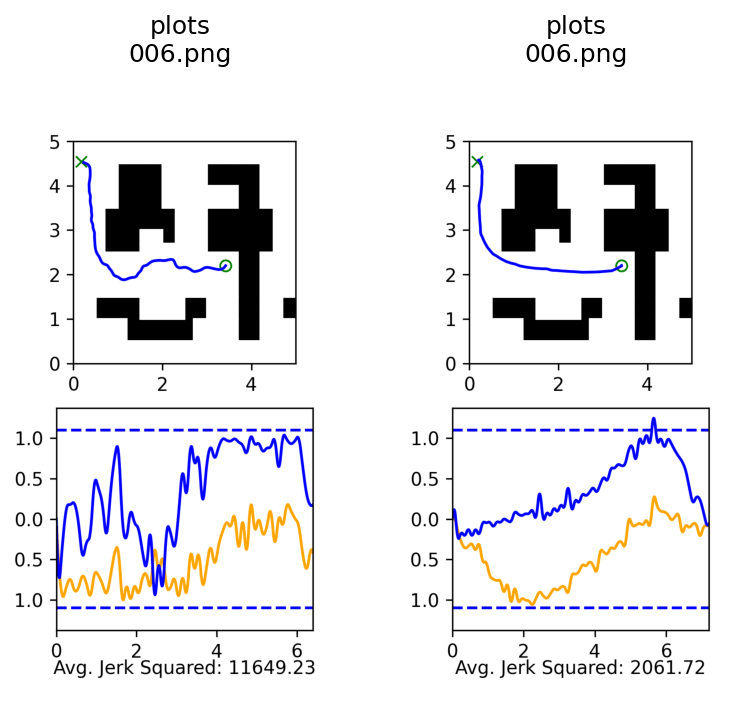
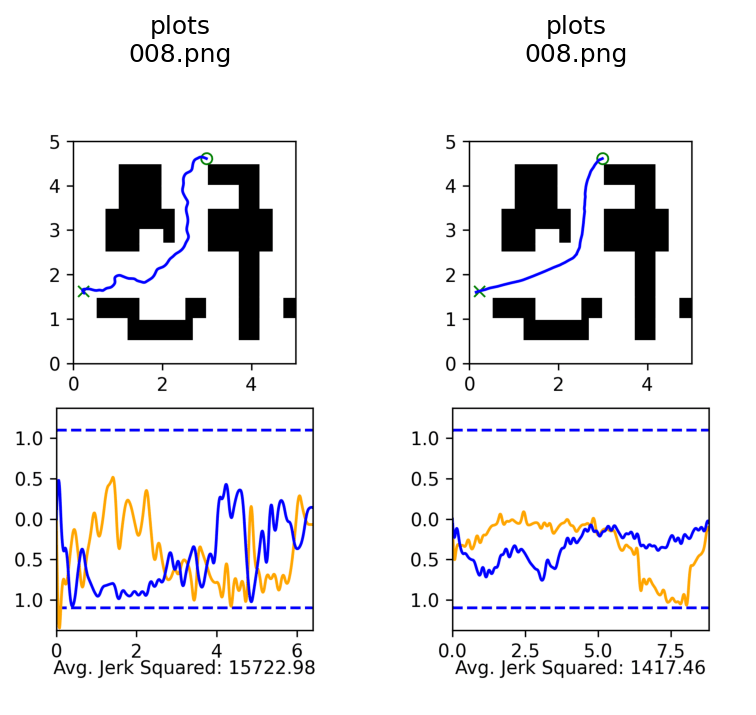
Experiment: RRT vs GCS
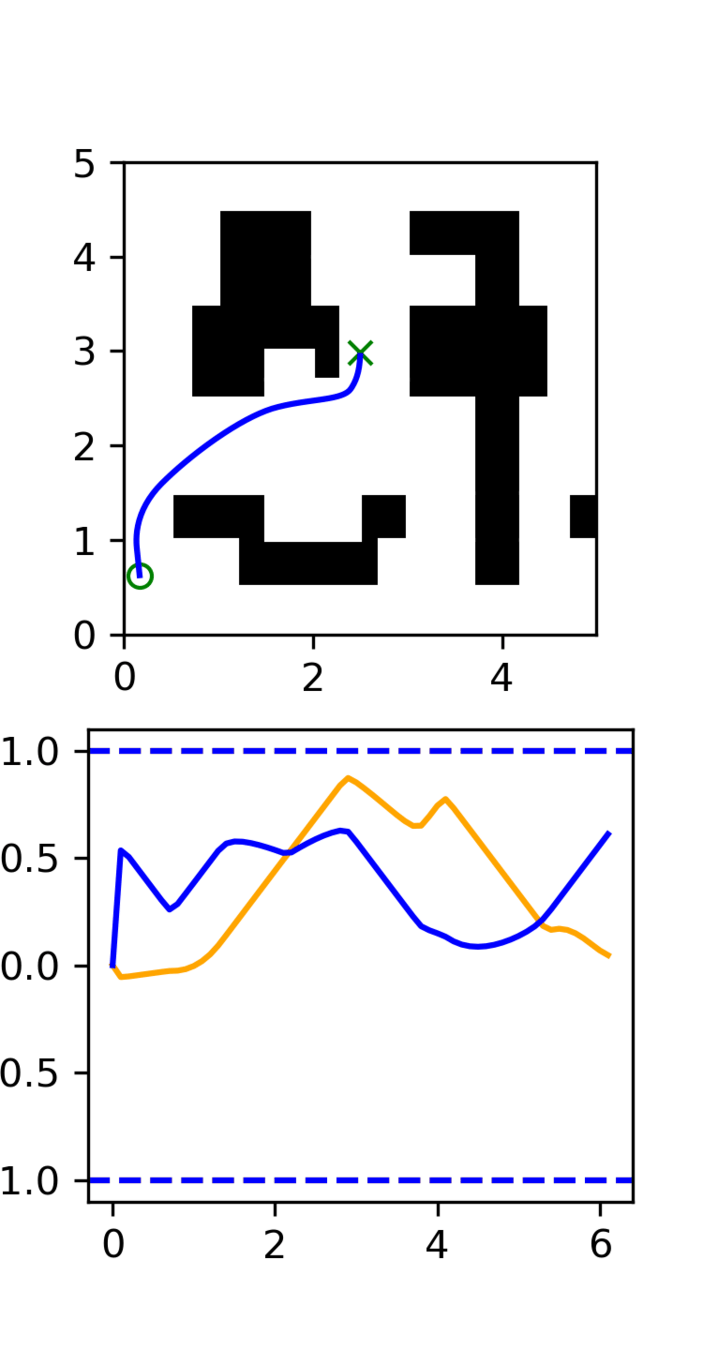
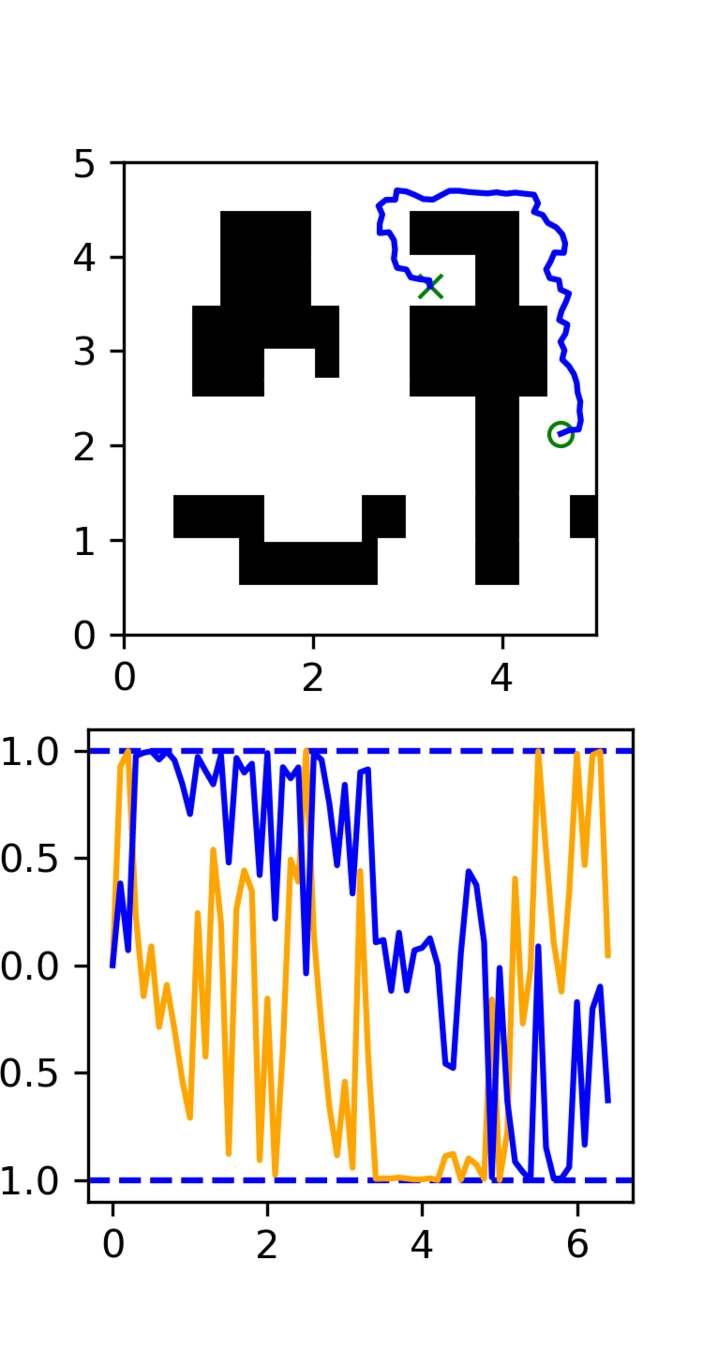
GCS
(clean)
RRT
(clean)
Task: Cotrain on GCS and RRT data
Goal: Sample clean and smooth GCS plans
- Example of high frequency corruption
- Common in robotics
- Low quality teleoperation or data gen
Baselines
Success Rate: 50%
Average Jerk Squared: 7.5k
100 GCS Demos
Success Rate: 99%
Average Jerk Squared: 2.5k
~5000 GCS Demos
Success Rate: 100%
Average Jerk Squared: 17k
~5000 RRT Demos
Cotraining vs Ambient Diffusion
Success Rate: 98%
Average Jerk Squared: 5.5k
Ambient: 100 GCS Demos, 5000 RRT Demos
Success Rate: 91%
Average Jerk Squared: 14.5k
Co-training: 100 GCS Demos, 5000 RRT Demos
Success Rate: 50%
Average Jerk Squared: 48.5k
GCS Only: 100 GCS Demos, 5000 RRT Demos
Cotraining vs Ambient Diffusion
Sim & Real Cotraining
"Clean" Data
"Corrupt" Data
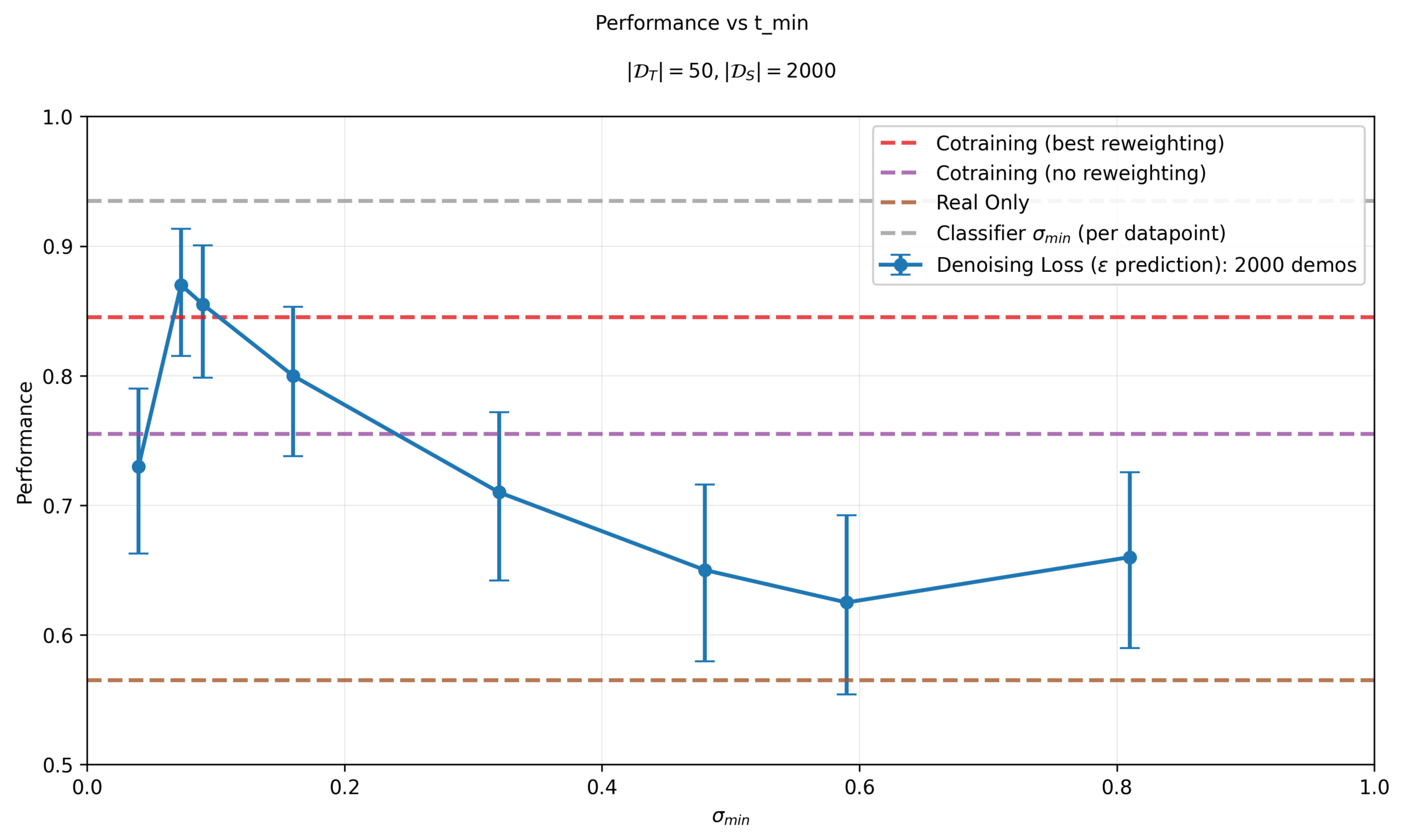
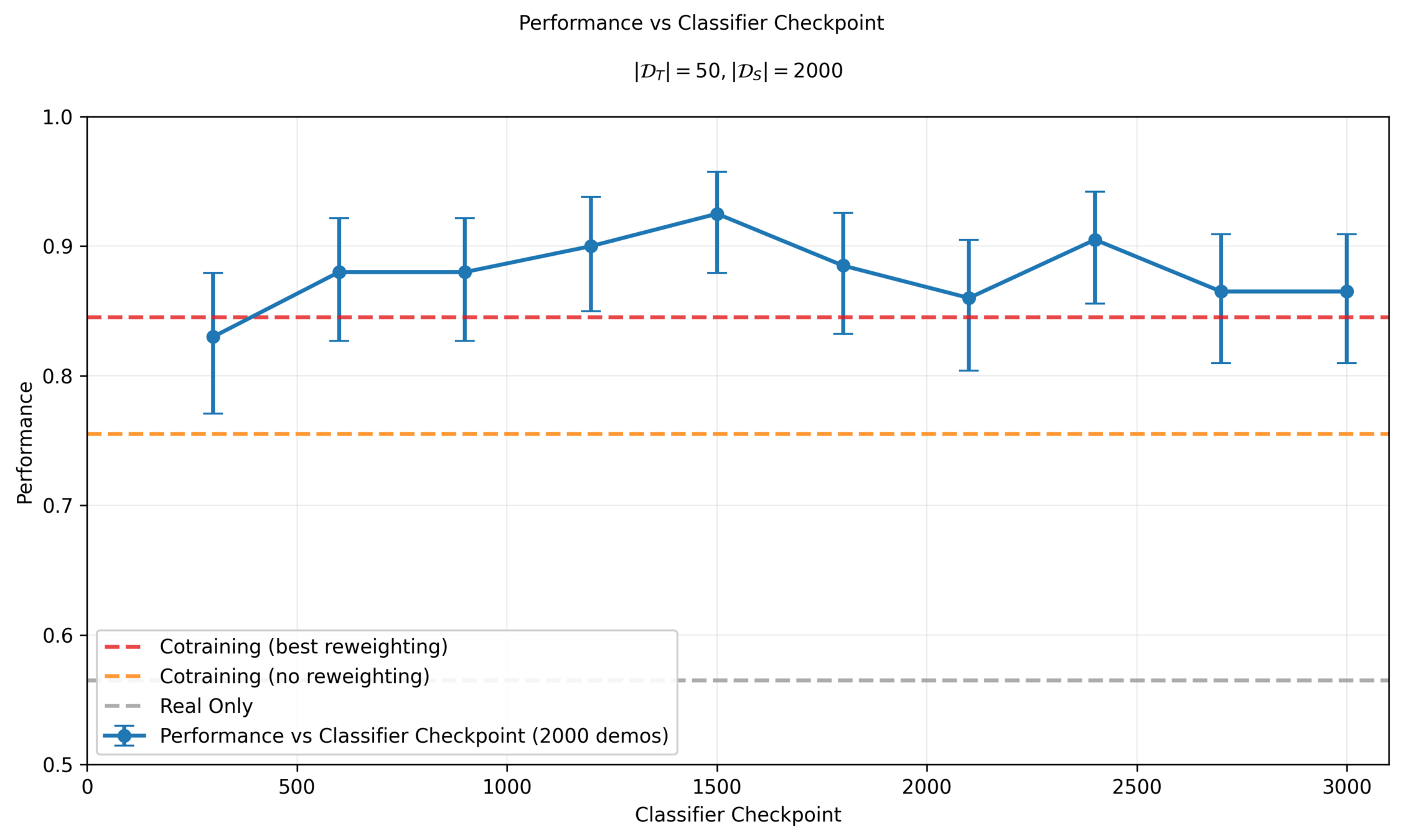
\(|\mathcal{D}_T|=50\)
\(|\mathcal{D}_S|=2000\)
Eval criteria: Success rate for planar pushing across 200 randomized trials
Sim & Real Cotraining
Sweep \(\sigma_{min}\) per dataset

Sim & Real Cotraining
Sweep \(\sigma_{min}\) per dataset

Sim & Real Cotraining
Performance vs Classifier Epoch
Sim & Real Cotraining
Performance vs Classifier Threshold
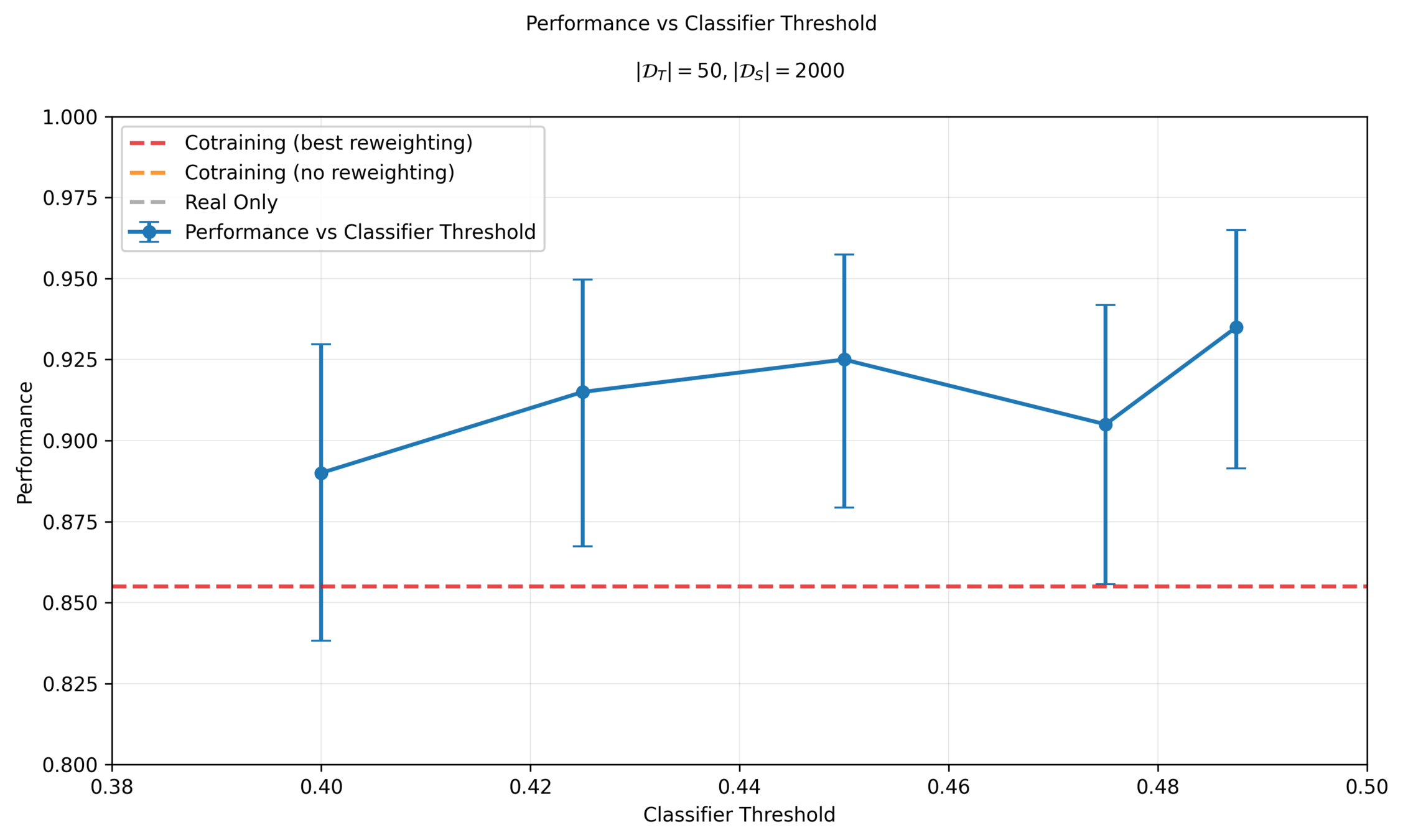
Sim & Real Cotraining
Performance vs Classifier Threshold

Sim & Real Cotraining
Performance vs Sim Demos: 10 Real Demos

Sim & Real Cotraining
Performance vs Sim Demos: 50 Real Demos

Sim & Real Cotraining
Performance vs Sim Demos: 150 Real Demos

Sim & Real Cotraining
Performance vs Sim Demos: 500 Real Demos

Sim & Real Cotraining
Performance vs Classifier Epoch
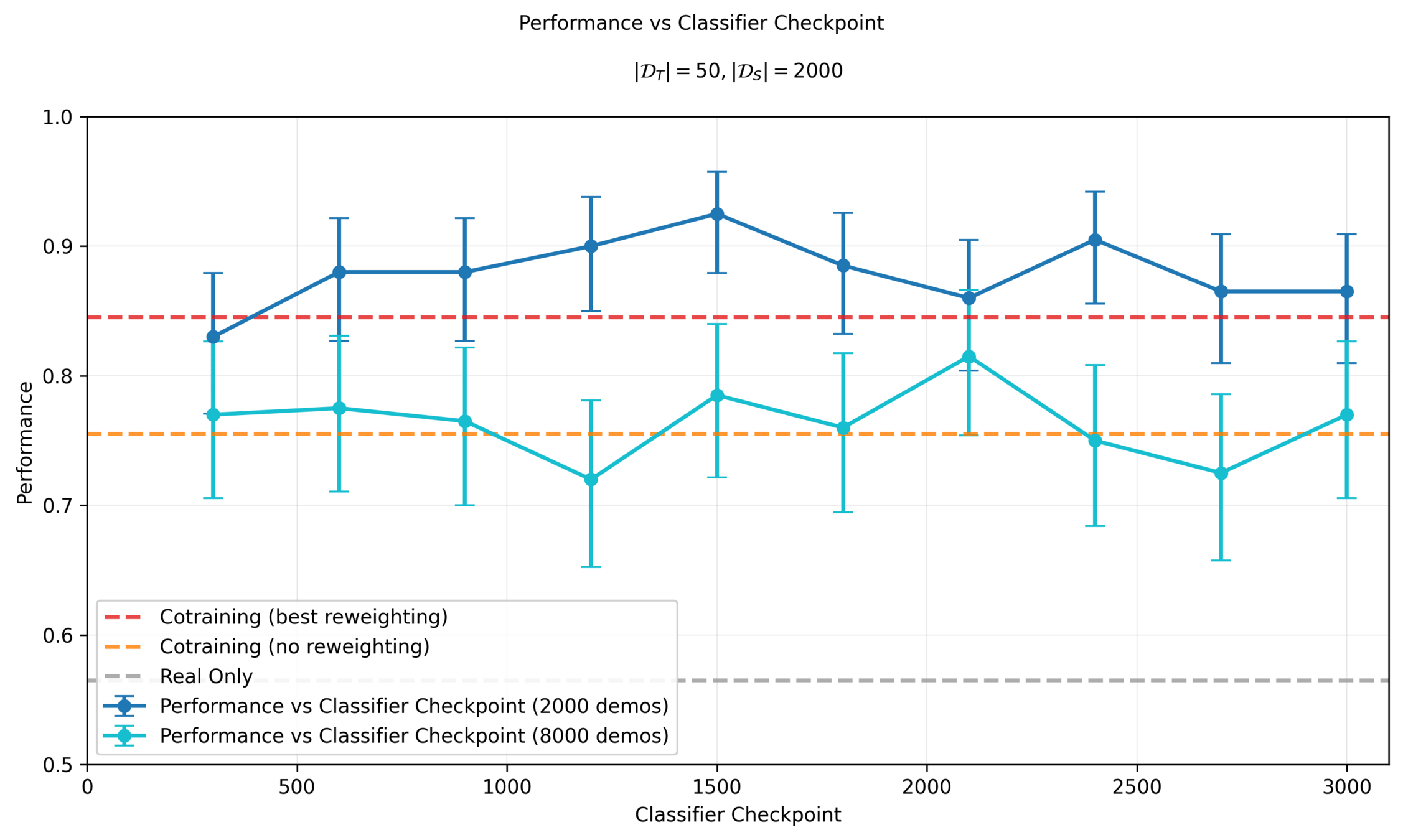
Denoising Loss vs Ambient Loss
Ambient Diffusion: Scaling \(|\mathcal{D}_S|\)
Hypothesis: As sim data increases, ambient diffusion approaches "sim-only" training, which harms performance.
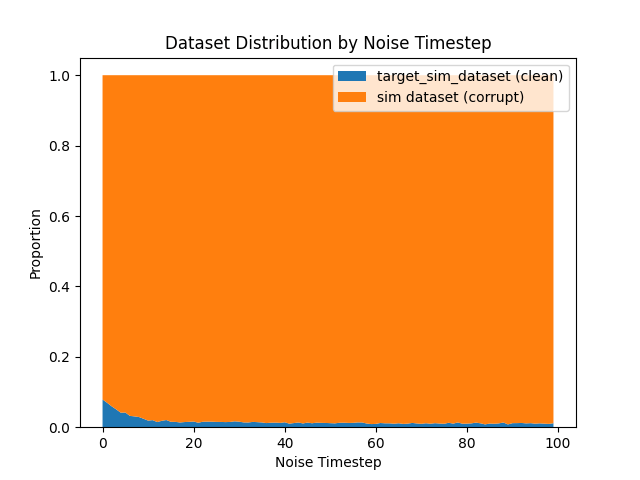
\(|\mathcal{D}_S|=500\)
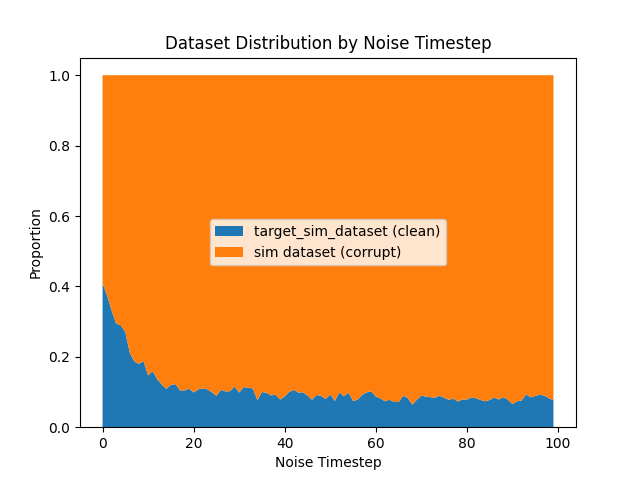
\(|\mathcal{D}_S|=8000\)
Denoising Loss vs Ambient Loss
Ambient Diffusion: Scaling \(|\mathcal{D}_S|\)
Hypothesis 1: Ambient Diffusion has plateau-ed.
- I think this is unlikely... although Giannis has an experiment to confirm this
Hypothesis 2: Softer version of ambient diffusion
- Instead of having a hard \(\sigma_{min}\) cutoff, use a softer version (i.e. use datapoints more for high noise levels, and less for lower noise levels)
- Need to figure out what this soft "mixing" function looks like
Denoising Loss vs Ambient Loss
Ambient Diffusion: \(\sigma_{max}\)
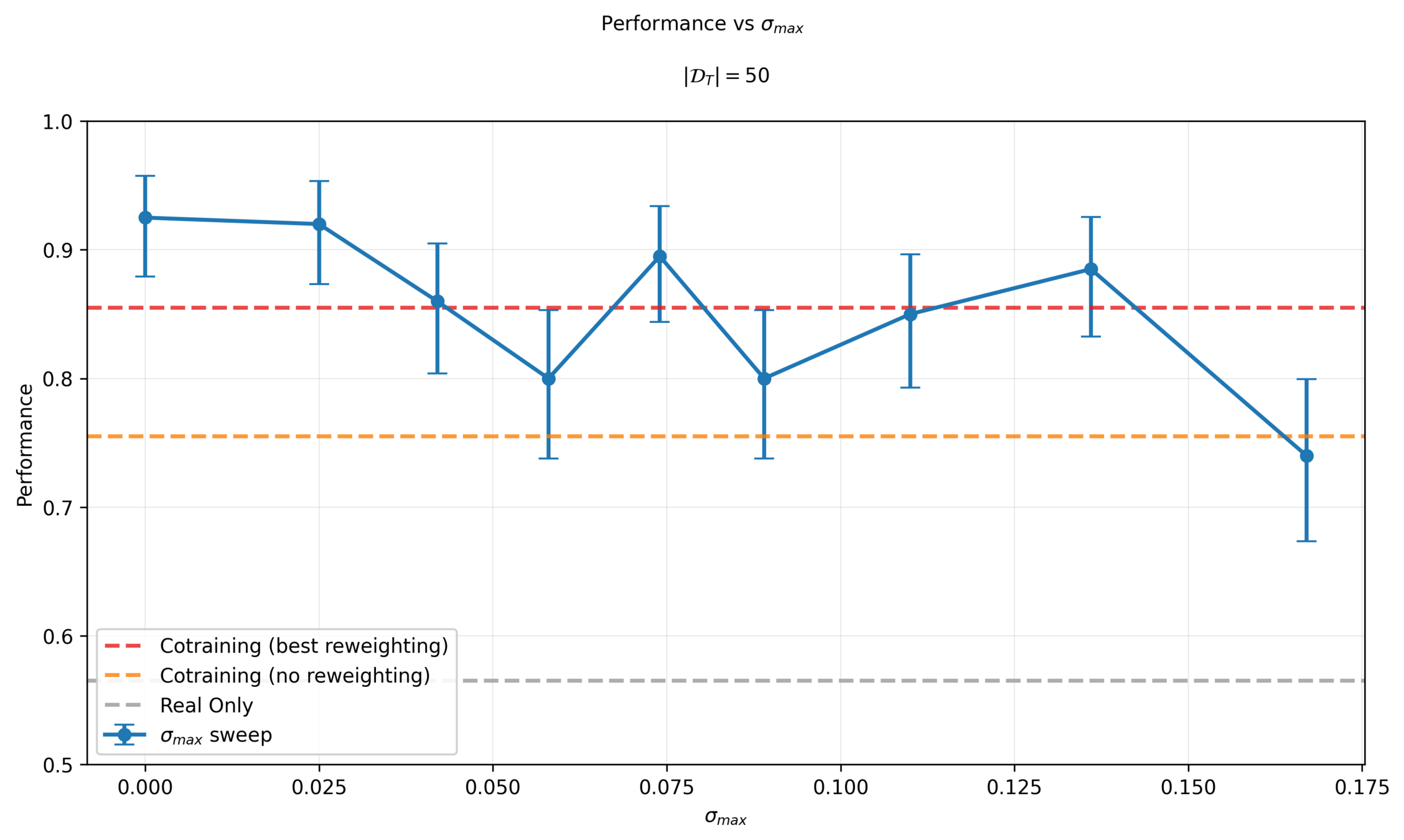
2025/09/03: Costis/Russ
By weiadam
2025/09/03: Costis/Russ
- 33



