PREPROCESSING  102

#NLP

Challenge #2

https://www.kaggle.com/c/cnam-niort-20192020/data

 

Deadline challenge & rapport : 5 avril

Outline

  1. Basics
  2. Count Features
    • Tf-IDF
    • N-Grams
  3. Dense vectors
    • Word2Vec
    • GloVe
  4. Deep learning & NLP

Basics

Library NLTK

import nltk
nltk.download()

Tokenize

from nltk.tokenize import sent_tokenize, word_tokenize
# Best for European languages

text = "Hey Bob! What's the weather at 8 o'clock"
sent_tokenize(text)
# ['Hey Bob!', "What's the weather at 8 o'clock"]
word_tokenize(sent_tokenize(text)[1])
# ['What', "'s", 'the', 'weather', 'at', '8', "o'clock"]

Part Of Speech Tagging

tokens = word_tokenize("I went to Paris to meet Bob")
nltk.pos_tag(tokens)
# [('I', 'PRP'),
#  ('went', 'VBD'),
#  ('to', 'TO'),
#  ('Paris', 'NNP'),
#  ('to', 'TO'),
#  ('meet', 'VB'),
#  ('Bob', 'NNP')]

nltk.ne_chunk(nltk.pos_tag(tokens), binary=True)
# Tree('S', [
#     ('I', 'PRP'), ('went', 'VBD'), ('to', 'TO'),
#     Tree('NE', [('Paris', 'NNP')]), ('to', 'TO'), ('meet', 'VB'),
#     Tree('NE', [('Bob', 'NNP')]),
# ])

POS tagger in NLTK isn't that great, if you want a good model, take a look at SyntaxNet

Stemming

Word -> Stem (non-changing portion)

# The two most used stemmers
from nltk.stem import SnowballStemmer
from nltk.stem.porter import PorterStemmer

snow = SnowballStemmer('english')

snow.stem("own") == snow.stem("owning") == snow.stem("owned")
# True

snow.stem("entities") == snow.stem("entity")
# True

Velocity: Snowball > Porter

Perf: Porter > Snowball

 

Lemmatisation

Word -> Lemma (dictionary form)

from nltk.stem import WordNetLemmatizer

wordnet = WordNetLemmatizer()

wordnet.lemmatize("women")
# u'woman'

wordnet.lemmatize("marketing")
# 'marketing'

wordnet.lemmatize("markets")
# u'market'

snow.stem("marketing")
# u'market'

snow.stem("markets")
# u'market'

/!\ Really slow /!\

Stop Words

from nltk.corpus import stopwords

len(stopwords.words('english'))
# 153

stopwords.words('english')[:20]
# [u'i',
#  u'me',
#  u'my',
#  u'myself',
#  u'we',
#  u'our',
#  u'ours',
#  u'ourselves',
#  u'you',
#  u'your',
#  u'yours',
#  u'yourself',
#  u'yourselves',
#  u'he',
#  u'him',
#  u'his',
#  u'himself',
#  u'she',
#  u'her',
#  u'hers']

String Metrics

 

Most widely used:

  1. Levenshtein distance (+++)
    • minimum number of character edits (insert, delete, substitue) to go from one word to the other
  2. Jaro-Winkler distance
    • Kinda the same but give more importance to the beginning of a word

Basic TODO

  1. Lowercase
  2. Normalize the punctuation; whatever your way, eg:
    • after a comma, always a space
    • every punctuation is turned to a space
  3. Normalize spaces: multiple to single
  4. Non-ASCII to ASCII: special characters, accents

Count Features

Count Vectorizer

Input: Corpus of text documents

Output: Matrix NxM with N = # of documents, M = # of unique words

from sklearn.feature_extraction.text import CountVectorizer

corpus = [
     'This is the first document.',
     'This is the second second document.',
     'And the third one.',
     'Is this the first document?',
 ]
vectorizer = CountVectorizer()
vectorizer.fit_transform(corpus).toarray()
# array([[0, 1, 1, 1, 0, 0, 1, 0, 1],
#        [0, 1, 0, 1, 0, 2, 1, 0, 1],
#        [1, 0, 0, 0, 1, 0, 1, 1, 0],
#        [0, 1, 1, 1, 0, 0, 1, 0, 1]])

vectorizer.get_feature_names()
# [u'and', u'document', u'first', u'is', u'one', u'second',
# u'the', u'third', u'this']

TF-IDF

tf(w, d) * idf(w)
\log \frac{|D|}{|\{d \in D: w \in d\}|}
f_{w,d}

Normalization of occurrence matrix:

Frequency of a word in a document, weighted by its rarity in the corpus

tf: reward for high occurrence in a document

idf: penalty if too much appearance in the corpus

 

(log term because, most of the time, words distribution across a corpus is a power law)

TF-IDF

import numpy as np
from sklearn.feature_extraction.text import TfidfVectorizer

corpus = [
     'This is the first document.',
     'This is the second second document.',
     'And the third one.',
     'Is this the first document?',
 ]
vectorizer = TfidfVectorizer()
np.around(vectorizer.fit_transform(corpus).toarray(), decimals=2)

# array([[ 0.  ,  0.44,  0.54,  0.44,  0.  ,  0.  ,  0.36,  0.  ,  0.44],
#        [ 0.  ,  0.27,  0.  ,  0.27,  0.  ,  0.85,  0.22,  0.  ,  0.27],
#        [ 0.55,  0.  ,  0.  ,  0.  ,  0.55,  0.  ,  0.29,  0.55,  0.  ],
#        [ 0.  ,  0.44,  0.54,  0.44,  0.  ,  0.  ,  0.36,  0.  ,  0.44]])

vectorizer.get_feature_names()
# [u'and', u'document', u'first', u'is', u'one', u'second',
# u'the', u'third', u'this']

N-Grams

from sklearn.feature_extraction.text import CountVectorizer

text = "word1 word2 word3 word4 word5"
CountVectorizer(ngram_range=(1,4)).build_analyzer()(text)
# [u'word1',
#  u'word2',
#  u'word3',
#  u'word4',
#  u'word5',
#  u'word1 word2',
#  u'word2 word3',
#  u'word3 word4',
#  u'word4 word5',
#  u'word1 word2 word3',
#  u'word2 word3 word4',
#  u'word3 word4 word5',
#  u'word1 word2 word3 word4',
#  u'word2 word3 word4 word5']


# Do the same, just with Python
def find_ngrams(input_list, n):
  return zip(*[input_list[i:] for i in range(n)])

Dense Vectors

Embedding

Embedding model learns to map each discrete word into a low-dimensional continuous vector-space from their distributional properties observed in some raw text corpus.

Embedding

Embedding

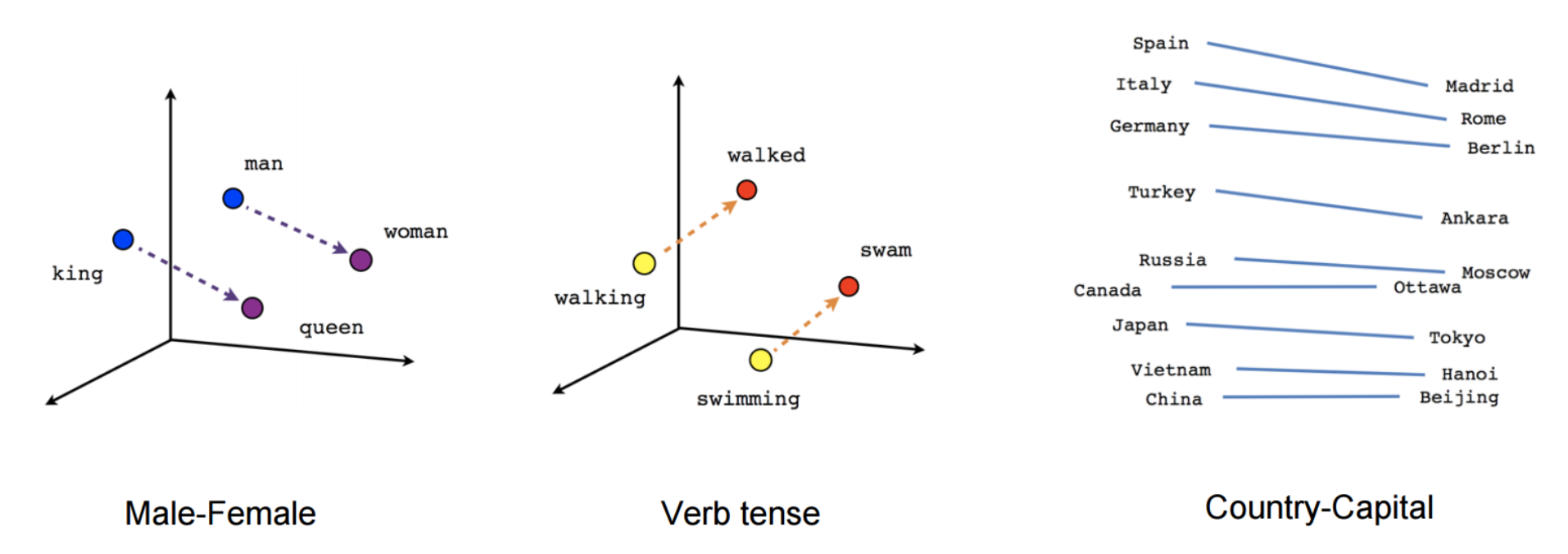
Word2Vec

Premise: words next to each other are related

 

Two distinct models:

  • CBOW (Continuous Bag of Words): given surrounding words, predict central word
  • SGNS (Skip Gram with Negative Sampling): given a word, predict surrounding words

Word2Vec: SGNS

Sentence: "The quick brown fox jumps over the lazy dog"

Window = 1                   Negative sample = 2

Word Context
the quick
quick the
quick brown
brown quick
brown fox
[...] [...]
Word False Context
the random_word1
the random_word2
quick random_word3
quick random_word4
brown random_word5
[...] [...]

Positive Dataset D (label 1)

Negative Dataset D' (label 0)

Word2Vec: SGNS

  • Considering:

    • Corpus of words w ∈ W and  their context c ∈ C

    • Parameters θ controlling the distribution  P(D = 1|w, c; θ)

v_c \in R^d, v_w \in R^d
P\left(D=1\middle|w,c;\theta\right) = \frac{1}{1 + e^{-v_c.v_w}}

Vectorial representation of w and c:

= {arg\,max}_\theta \displaystyle\sum_{(w, c) \in D} log \frac{1}{1 + e^{-v_c.v_w}} + \displaystyle\sum_{(w, c) \in D'} log \frac{1}{1 + e^{v_c.v_w}}

Probability that a couple (w, c) belongs to D:

Objective:

{arg\,max}_\theta \displaystyle\prod_{(w, c) \in D} P\left(D=1\middle|w,c;\theta\right) \displaystyle\prod_{(w, c) \in D'} P\left(D=0\middle|w,c;\theta\right)

Word2Vec: in pratice

Python library gensim: https://radimrehurek.com/gensim/models/word2vec.html

2 methods:

Usually, people use a lot of pre-trained Word2Vec models!

A lot of built-in functions:

import gensim
import pandas as pd

# Method 1: Train your own model
train = pd.read_csv('train.csv', encoding="ISO-8859-1")
sentences = train[['product_title', 'search_term']].values.flatten()
model = Word2Vec(sentences, size=100, window=5, negative=5, alpha=0.025, min_count=10)

# Use a pre-trained model
# Download there: https://drive.google.com/file/d/0B7XkCwpI5KDYNlNUTTlSS21pQmM/edit
model = gensim.load_word2vec_format('GoogleNews-vectors-negative300.bin.gz')
print(model.words)  # list of words in dictionary
print(model['king'])  # get the vector of the word 'king'

Word2Vec: in pratice

model.wv.most_similar(positive=['woman', 'king'], negative=['man'])
# [('queen', 0.50882536), ...]

model.wv.doesnt_match("breakfast cereal dinner lunch".split())
# 'cereal'

model.similarity('france', 'spain')

A lot of built-in functions:

GloVe

Another embedding method:

  • Word2vec is a "predictive" model
  • GloVe is a "count-based" model

Count-based models:

Learn their vectors by doing some dimensionality reduction on the co-occurence counts matrix.

 

Always the same objective: minimize some "construction loss" when trying to find the lower-dimensional representation which can explain most of the variance in the high-dimensional data.

GloVe: quick insight

tl;dr: normalizing the counts & log-smoothing

 

Weighting the counts around the window:

Sentence: "word1 word2 word3 word4"

Window: 2

 

 

 

 

word1 word2 word3 word4
word1 0 1 0.5 0
word2 1 0 1 0.5
word3 0.5 1 0 1
word4 0 0.5 1 0

GloVe: quick insight

Based on this matrix, vectors are built using:

 

 

Where Xij is the element (i,j) of the co-occurence matrix

w_i^Tw_j + b_i + b_j = log X_{i,j}
\displaystyle\sum_{(i, j) = 1}^{V} g(X_{i,j}) (w_i^Tw_j + b_i + b_j - log X_{i,j})^2

Weight function g:

Cost function:

g(X_{i,j}) = \left\{\frac{X_{i,j}}{x_{max}} \text{ if }X_{i,j} < x_{max} \text{ else 1}\right\}

GloVe: in practice

Python library & pre-trained models:

https://github.com/stanfordnlp/GloVe

Fast-Text

State Of the Art for word embedding

Library:

https://github.com/facebookresearch/fastText

Pre-trained models for 294 languages: https://github.com/facebookresearch/fastText/blob/master/pretrained-vectors.md

# pip install fasttext
import fasttext

import scipy
import numpy as np

model = fasttext.load_model('model.bin')
print(model.words) # list of words in dictionary
print(model['king']) # get the vector of the word 'king'

stop = []  # Stop words?

def cos_similarity(data_1, data_2):
    # Embedding for a sentence = mean of word embedding. Could it be better?
    sent1_emb = np.mean([model[x] for word in data_1 for x in word.split() if x not in stop], axis=0)
    sent2_emb = np.mean([model[x] for word in data_2 for x in word.split() if x not in stop], axis=0)
    
    return 1. - scipy.spatial.distance.cosine(sent1_emb, sent2_emb)

Fast-Text

whatisit

 

Fasttext is essentially an extension of word2vec model.

It treats each word as composed of character ngrams. So the vector for a word is made of the sum of this character n grams.

For example the word vector “apple” is a sum of the vectors of the n-grams “<ap”, “app”, ”appl”, ”apple”, ”apple>”, “ppl”, “pple”, ”pple>”, “ple”, ”ple>”, ”le>” (assuming hyperparameters for smallest ngram[minn] is 3 and largest ngram[maxn] is 6)

Fast-Text

advantages

 

  • Rare words
  • OOV words
  • In theory, using character level embeddings seem to improve performances (but at a huge computational cost)

Problème : Le contexte

 

I like to eat my cereals with an apple.
Apple is a highly profitable company.

 

 

Le mot "Apple" est représenté par un seul vecteur dans l'espace.

 

Envie :

Avoir une représentation du mot "Apple" dans une région de l'espace avec de la nourriture pour la première phrase et une autre représentation dans une région avec des noms d'entreprise pour la deuxième phrase.

Optionnal:

Bert & Friends

Aller plus loin

Best course:

CS224D

Youtube Playlist

Syllabus

 

Do it, do it, do it! (and do the maths)

Useful Tool:

https://projector.tensorflow.org/

 

 

T-SNE?

https://mlexplained.com/2018/09/14/paper-dissected-visualizing-data-using-t-sne-explained/

U-MAP?

https://pair-code.github.io/understanding-umap/

 

U-MAP > T-SNE

Min(challenge):

 

  1. Apply some cleaning & standardization for the textual data
  2. Build smart feature engineering based on TF-IDF (TF-IDF is a sparse vector space model for words / sentences)
  3. Same with at least an embedding metho : Word2Vec (gensim) is the easier; either re-use a pre-trained model or build your own w2v model

Preprocessing 102

By Yann Carbonne

Source: ycarbonne

Preprocessing 102

  • 772

More from Yann Carbonne