Number Theory
yennnn
數論基本認識
什麼是數論?
研究整數性質的數學分支
質數與因數
- 若 \(b = ak\) 且 \(a, b, k \in \mathbb{Z}\) 則稱 \(a\) 為 \(b\) 的因數
- 若 \(n \in \mathbb{N}, n > 1\) 且 \(n\) 只有 \(1\) 和 \(n\) 兩個正因數
則 \(n\) 為質數(prime)
反之,則稱 \(n\) 為合數
標準分解式
- 算術基本定理
- \(\forall n \in \mathbb{N}, n > 1,n皆可唯一表示為若干個質數的乘積\)
n = {p_1}^{\alpha_1}{p_2}^{\alpha_2}......{p_n}^{\alpha_n}\\
{p_i} \in prime\\
\alpha_i \in \mathbb{N}
標準分解式
標準分解式與因數
- 正因數的數量\( = \prod_{i = 1}^{n} (\alpha_i + 1)\)
n = {p_1}^{\alpha_1}{p_2}^{\alpha_2}......{p_n}^{\alpha_n}\\
- \(正因數和 = \prod_{i = 1}^{n} \frac{p_{i}^{\alpha_i + 1} - 1}{p_{i} - 1}\)
- \(正因數積 = \sqrt n^{正因數數量}\)
- 完美數Perfect Number:\(若n的真正因數和= n 則稱 n 為完美數\)
\(eg:28 = 1 + 2 + 4 + 7 + 14\)
質數小性質
- 質數的數量有\(\infty\)個
- 質數的密度
\[ \pi(n) \approx \frac{n}{\ln n}\]
來點演算法吧
終於講完先備知識了
判定質數
\(若k為合數,則必有k = mn,其中k, m, n \in \mathbb{N}\)
\(且必有m \leq \sqrt k或n \leq \sqrt k\)
bool prime(int n) {
if (n < 2) return false;
for (int x = 2; x*x <= n; x++) {
if (n%x == 0) return false;
}
return true;
}複雜度:\(O(\sqrt n)\)
質因數分解
就...一直除以質因數
vector<int> factors(int n) {
vector<int> f;
for (int x = 2; x*x <= n; x++) {
while (n%x == 0) {
f.push_back(x);
n /= x;
}
}
if (n > 1) f.push_back(n);
return f;
}複雜度:\(O(\sqrt n)\)
建立質數表
一個一個找出來
vector<int> prime(0);
int prime_table(){
prime.push_back(2);
for (int j = 3; j <= 2147483647; j++) {
if (isPrime(j)) {
prime.push_back(j);
}
}
return 0;
}
bool isPrime(int n) {
if (n < 2) return false;
for (int x = 0; prime[x]*prime[x] <= n; x++) {
if (n%prime[x] == 0) return false;
}
return true;
}複雜度:\(O(n\sqrt n)\)
可以再快一點嗎?
埃拉托斯特尼篩法
國小課本好像有提過(?
找出一個質數,
它的倍數都不是質數
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
for (int x = 2; x <= n; x++) {
if (sieve[x]) continue;
for (int u = x*x; u <= n; u += x) {
sieve[u] = 1;
}
}複雜度:\(O(n \log \log n)\)
最大公因數
歐幾里得演算法 aka 輾轉相除法
\(gcd(a, b) = gcd(b, a\%b)\)
int gcd(int a, int b) {
if (b == 0) return a;
return gcd(b, a%b);
}複雜度:\(O(log n)\)
不定方程
\(ax + by = c\)
條件:
\(ax + by = c存在整數解 若且唯若 gcd(a, b) \mid c\)
要怎麼解不定方程ㄋ?
擴展歐幾里得演算法!
已知bx + (a \% b) y = 1的一組正整數解\\
該怎麼推出ax + by = 1的解?
bx + (a \% b)y = 1\\
bx + (a - b \times \lfloor\frac{a}{b}\rfloor)y = 1\\
bx + ay - b \times \lfloor\frac{a}{b}\rfloor \times y = 1\\
b(x - \lfloor\frac{a}{b}\rfloor \times y) + ay = 1\\
ay + b(x - \lfloor\frac{a}{b}\rfloor \times y) = 1\\
x' = y\\
y' = x - \lfloor \frac{b}{a} \rfloor \times y\\
所以我們可以遞迴解
void extgcd(int a, int b, int& x, int& y, int& d) {
if (b == 0) {
d = a;
x = 1;
y = 0;
return;
}
else {
extgcd(b, a % b, x, y, d);
int nx = y;
int ny = x - (a / b) * y;
x = nx;
y = ny;
return;
}
}
複雜度:\(O(log n)\)
快速冪
要怎麼算\(a ^ {m}\)
\(a \times a \times a \times...... \times a\)
複雜度:\(O(n)\)
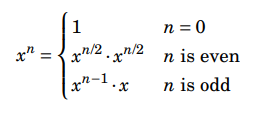
int modpow(int x, int n, int m) {
if (n == 0) return 1;
if(n % 2 == 1) return (x * modpow(x, n - 1, m)) % m;
long long u = modpow(x, n/2, m);
return (u * u) % m;
}複雜度:\(O(log n)\)
求\(x ^ n \ mod \ m\)
同餘
- \[若a = bq + r且a, b, q, r \in \mathbb{Z}\]
我們記為\(a \equiv r \pmod b\)
- 若\(x \equiv a \pmod m, y \equiv b \pmod m\)
- 則\(x + y \equiv a + b \pmod m\)
- \(x - y \equiv a - b \pmod m\)
- \(x \times y \equiv a \times b \pmod m\)
- \(x / y \equiv a / b \pmod m\)
可是我好想做除法怎麼辦
模逆元!!!
若\(ax \equiv 1 \pmod m\)
\(我們稱a為x的模逆元,記作x^{-1}\)
模逆元存在條件:
\(gcd(a, m) = 1\)
費馬小定理
a^{p-1} \equiv 1 \pmod p
所以\(a^{p - 2} \)為 \(a\) 的模逆元
歐拉定理
\[a ^ {\varphi(m)} \equiv 1 \pmod m\]
\varphi(m) = \prod_{i = 1}^{k} p_{i}^{\alpha{i}} (p_i - 1)
所以\(a^{\varphi(m) - 1} \)為 \(a\) 的模逆元
\[解ax - bm = 1\]
用擴展歐幾里得演算法
Thanks for Listening
Number Theory
By yennnn
Number Theory
- 598


