時間複雜度
yennnn
如何衡量一支程式碼的效能?
如何衡量一支程式碼的效能?
- 執行所需時間
- 記憶體空間
- 編程難易度
- ......
如何衡量一支程式碼的效能?
- 執行所需時間
- 記憶體空間
- 編程難易度
- ......
編程時間
占用的記憶體空間
實際執行一次花了多久
如果我們以實際執行時間來描述程式的效能......
- 每次跑會一樣嗎?
- 在不同的電腦上會一樣嗎?
- 輸入不同的時候會一樣嗎?
我們需要一個更一般化的理論來分析
如果我們以程式的步驟數來描述程式的效能......
- 不受電腦硬體的影響
- 可能受輸入規模影響
- 可以把步驟數想成一個函數\(T(n),n是輸入規模\)
怎麼算\(T(n)\)呢?
計算\(T(n)\)
- 我們把變數的宣告、運算、比較等等各種操作都均等的視為1個步驟
- \(T(n) = 程式從開始執行到結束總共經過幾個步驟\)
- 注意迴圈、遞迴等等
計算\(T(n)\)
Ex1:n個整數的總和
int sum(int list[], int n){
int i;
int result = 0;
for(int i = 0; i < n; i++){
result = result + list[i];
}
return result;
}Ex1:n個整數的總和
int sum(int list[], int n){
int i;
int result = 0;
for(int i = 0; i < n; i++){
result = result + list[i];
}
return result;
}\(1\)
\(1\)
\(2(n + 1) + 1\)
\(n\)
\(1\)
每行計算步驟數
\(3n + 6\)
\(T(n) = 3n + 6\)
Ex2:兩個二維陣列相加
array_add(int m, int n, int A[m][n], int B[m][n], int C[m][n]){
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
C[i][j] = A[i][j] + B[i][j];
}
}
}Ex2:兩個二維陣列相加
array_add(int m, int n, int A[m][n], int B[m][n], int C[m][n]){
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
C[i][j] = A[i][j] + B[i][j];
}
}
}每行執行步驟
\(2(m + 1) + 1\)
\(2(m + 1) + 1\)
\(2m(n + 1) + 1\)
\(mn\)
\(T(n) = 2mn + 4m + 4\)
#include <iostream>
#define MAXN 200100
#define INF 2147483647
using namespace std;
int arr[MAXN];
class segment_tree {
public:
void init(int n) { fill(seg_arr, seg_arr + 4 * n, INF); }
void build(int l, int r, int cur) {
if (l == r) {
seg_arr[cur] = arr[l];
return;
}
int mid = (l + r) / 2;
build(l, mid, cur * 2);
build(mid + 1, r, cur * 2 + 1);
seg_arr[cur] = min(seg_arr[cur * 2], seg_arr[cur * 2 + 1]);
return;
}
void modify(int l, int r, int ind, int val, int cur) {
if (l == r && l == ind) {
arr[ind] = val;
seg_arr[cur] = val;
return;
}
int mid = (l + r) / 2;
if (ind <= mid) {
modify(l, mid, ind, val, cur * 2);
} else {
modify(mid + 1, r, ind, val, cur * 2 + 1);
}
seg_arr[cur] = min(seg_arr[cur * 2], seg_arr[cur * 2 + 1]);
return;
}
int query(int l, int r, int ql, int qr, int cur) {
if (l > r || ql > r || qr < l) return INF;
if (l >= ql && r <= qr) return seg_arr[cur];
int mid = (l + r) / 2;
// cout << l << ' ' << r << '\n';
return min(query(l, mid, ql, qr, cur * 2),
query(mid + 1, r, ql, qr, cur * 2 + 1));
}
void print(int n) {
for (int i = 0; i <= 4 * n; i++) {
cout << "seg_arr[" << i << "] = " << seg_arr[i] << '\n';
}
}
protected:
int seg_arr[MAXN * 4];
};
segment_tree seg;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n, q;
cin >> n >> q;
fill(arr, arr + n + 10, INF);
seg.init(n);
for (int i = 1; i <= n; i++) {
cin >> arr[i];
}
seg.build(1, n, 1);
// seg.print(n);
while (q--) {
int m, a, b;
cin >> m >> a >> b;
if (m == 1) {
seg.modify(1, n, a, b, 1);
} else {
cout << seg.query(1, n, a, b, 1) << '\n';
}
}
return 0;
}Ex3: 線段樹
這樣要怎麼分析?==
\(Big \ \mathcal{O} \ notation\)
- 精確算出\(T(n)\)實在太麻煩了
- 我們也不需要那麼精確的得知\(T(n)\)即可估算時間複雜度
- 找到一個簡單的函數\(f(n)\)來代表所有\(T(n)和f(n)\) 差不多 的程式
- 我們會用\(Big \ \mathcal{O} \ notation\) 這樣的表達方式來表達這樣的近似關係
- Eg : \( \mathcal{O} (n) \)
時間複雜度
有時候我們在估計程式的時間複雜度\(T(n)\)時
其實也沒有那麼在意程式在每個\(n\)的精確表現
我們更在意的是\(T(n)\)隨\(n\)的成長趨勢
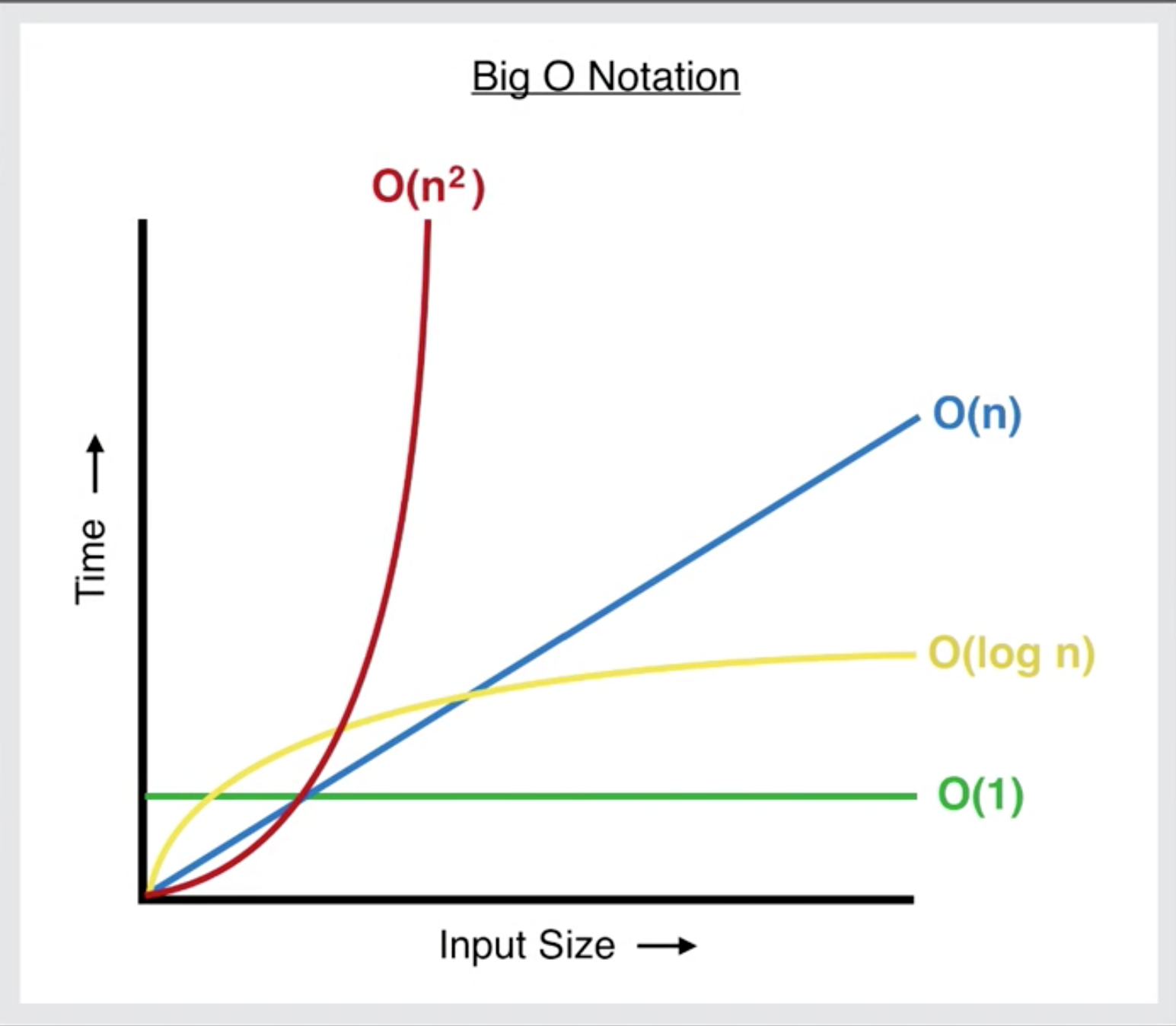
- 表達一個函數的 漸近上界
- 以\(\mathcal{O} (f(n)) \)表示 \(f(n)是T(n)的漸近上界\)
- 隨著\(n\)的成長,\(T(n)\)也會隨之成長,但\(T(n)\)的成長不會超過\(f(n)\)
一些常見的複雜度比較
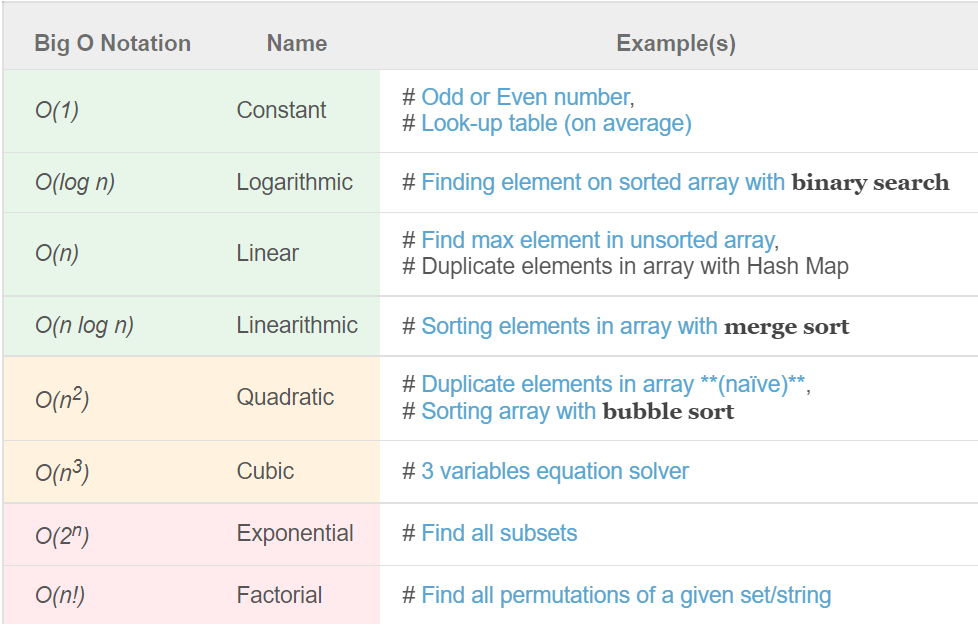
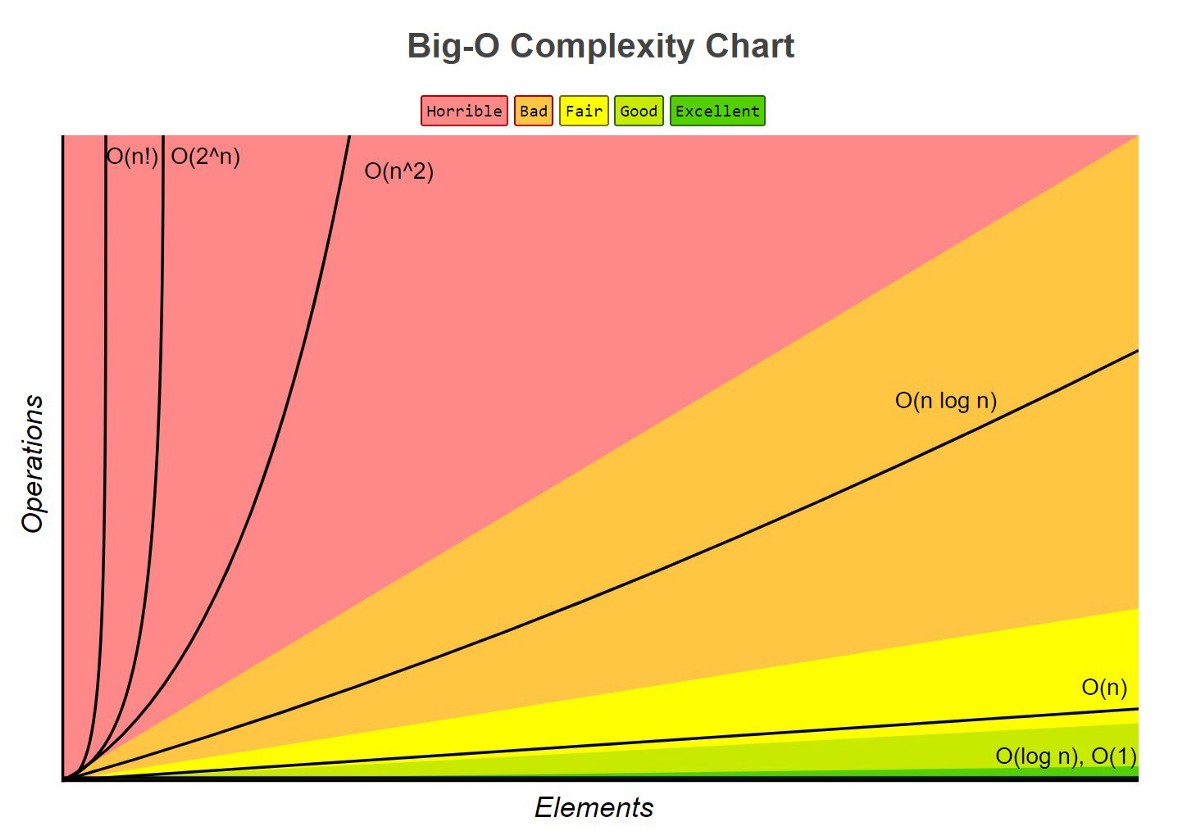
複雜度的成長趨勢
一些常見的複雜度比較

成長越快
階數越高
\(Big \ \mathcal{O} \ notation\)估算法則
-
加法定則
-
數個函數相加,取階數最高者代表複雜度
-
-
乘法定則
-
函數乘以常數可省略
-
\(Big \ \mathcal{O} \ notation\)估算法則
-
加法定則
-
\(n\)
-
\(n^2 + n\)
-
\(n + \log n\)
-
\(n + n \log n\)
-
\(2^n + n^2\)
-
\(\mathcal{O}(n)\)
\(\mathcal{O}(n^2)\)
\(\mathcal{O}(n)\)
\(\mathcal{O}(n \log n)\)
\(\mathcal{O}(2^n)\)
\(Big \ \mathcal{O} \ notation\)估算法則
-
乘法定則
-
\(n\)
-
\(2n\)
-
\((\log 2) + n\)
-
\((\log 2)n\)
-
\(\log (2n)\)
-
\(\log_{7122} n\)
-
\(\mathcal{O}(n)\)
\(\mathcal{O}(n)\)
\(\mathcal{O}(n)\)
\(\mathcal{O}(\log n)\)
\(\mathcal{O}(n)\)
\(\mathcal{O}(\log n)\)
\(Big \ \mathcal{O} \ notation\)估算實戰
-
快速估算仰賴對基本演算法與資料結構的複雜度認識
- Ex :
- sort : \( \mathcal{O} (n \log n)\)
- 二分搜 : \( \mathcal{O} ( \log n)\)
- set插入 : \( \mathcal{O} ( \log n)\)
- dijkstra : \( \mathcal{O} ( (E + V) \log V)\)
- kruskal : \( \mathcal{O} (E \log V)\)
- ......
vector<int> a;
sort(a.begin(), a.end());\( \mathcal{O} (n \log n)\)
vector<int> a[n];
for(int i = 0; i < n; i++)
sort(a[i].begin(), a[i].end());\( \mathcal{O} (n^2 \log n)\)
vector<int> a[n];
for(int i = 0; i < n; i++)
a[i].push_back(1);
sort(a[i].begin(), a[i].end());\( \mathcal{O} (n + n \log n) = \mathcal{O} (n \log n)\)
時間複雜度
By yennnn
時間複雜度
0325資訊社 社課講義--時間複雜度 Time Complexity Designed By Yennnn
- 480


