DeepRetina

Yigit DEMIRAG

Reyhan ERGUN

Gokhan GOK

Neural Network Performances on

MNIST Handwritten Digits Database

BILKENT - 2015

Outline

  • MNIST Database
  • kNN, SVM
  • Two Layer Feed Forward Network
  • Convolutional Neural  Network
  • Convolutional Deep Neural Networks

MNIST Database

  1. ​60k training, 10k test images
  2. 28x28 pixel size
  3. Black/White, size-normalized and centered.
  4. Currently one of the leading database for testing neural networks (CIFAR-10, SVHN etc.)

k-Nearest Neighbourhood

  1.  No training required.
  2. Algorithm:

Input:   D, the set of K-training objects, and test object

Process:

 

Compute                 , the distance between z and every object, 

Select                       , the set of k closest training objects to z.

 

Output: 

(x,y) \in D
(x,y)∈D(x,y) \in D
d(x',x)
d(x′,x)d(x',x)
z= (x',y')
z=(x′,y′)z= (x',y')
D_z \subseteq D
Dz⊆DD_z \subseteq D
y' = \arg\max_{v} \Sigma_{(x_i,y_i) \in D} I(v= y_i)
y′=argmaxvΣ(xi,yi)∈DI(v=yi) y' = \arg\max_{v} \Sigma_{(x_i,y_i) \in D} I(v= y_i)

k-Nearest Neighbourhood - Results

Accuracy : 96.13%

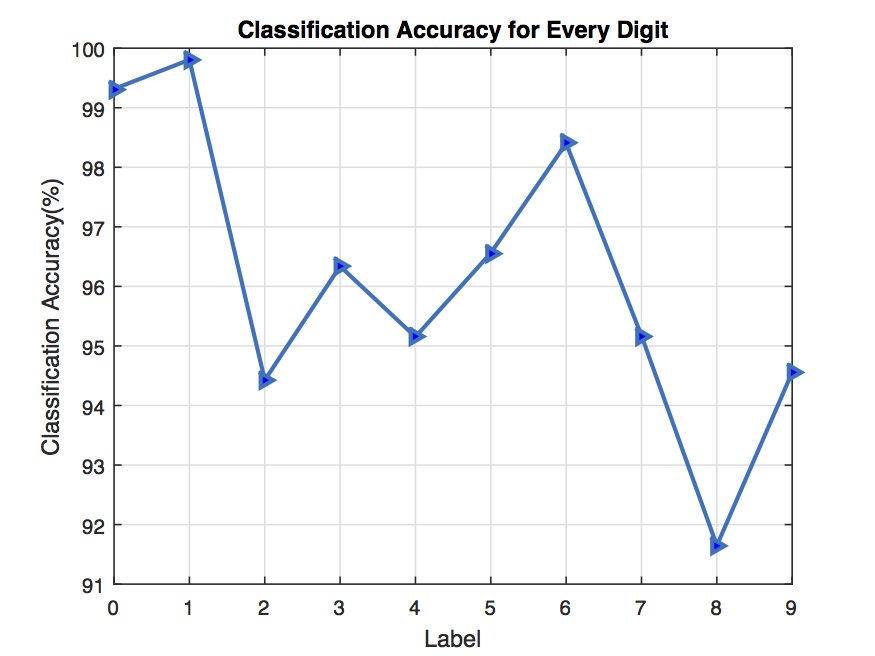
k-Nearest Neighbourhood - Results

Pros:

  1. High accuracy
  2. Insensitive to outliers
  3. No assumption to data

 

Cons: 

  1. Computationally expensive
  2. Requires a lot memory
  3. No hierarchical structure is captured.

SVM - Calculations

  1. Instead of dealing P, we deal with D (used MATLAB quadprog(), input matrix, and vectors calculated as shown in our lecture)
  • Determined the optimum Lagrange multipliers 

        i.e.             from the result of quadprog().

  • Compute the optimum weight vector as

    

 

  • Compute the optimum bias as

​

 

 

  • Average       found for each SV, (since we obtained a different       for each SV)
\alpha_{o,i}
αo,i\alpha_{o,i}
\mathbf{w_o} = \sum\limits_{i=1}^{N_s} \alpha_{o,i} d_i \mathbf{x}_i
wo=∑i=1Nsαo,idixi\mathbf{w_o} = \sum\limits_{i=1}^{N_s} \alpha_{o,i} d_i \mathbf{x}_i
b_o = 1 - \mathbf{w}_o^T \mathbf{x}^{(s)}
bo=1−woTx(s)b_o = 1 - \mathbf{w}_o^T \mathbf{x}^{(s)}
\text{ for } d^{(s)} = 1
 for d(s)=1\text{ for } d^{(s)} = 1
= 1 - \sum\limits_{i=1}^{N_s} \alpha_{o,i} d_i \mathbf{x}_i^T \mathbf{x}^{(s)}
=1−∑i=1Nsαo,idixiTx(s)= 1 - \sum\limits_{i=1}^{N_s} \alpha_{o,i} d_i \mathbf{x}_i^T \mathbf{x}^{(s)}
b_o
bob_o
b_o
bob_o

SVM - Setup

 

2.    Used as one vs rest classifier to deal with less number of SVMs.

3.    4000 training data with equally likely distribution.

4.    Used highest probability result when more than one binary SVM
        estimated a label.

5.    Used highest probability "non reported" result when none of the   

        binary SVM estimated a label.

SVM - Results

N T SV L Acc
Label 0 vs Rest 4000 500 2760 Inf
Label 1 vs Rest 4000 500 431 Inf
Label 2 vs Rest 4000 500 2996 Inf
Label 3 vs Rest 4000 500 4000 Inf
Label 4 vs Rest 4000 500 3638 Inf
Label 5 vs Rest 4000 500 3998 Inf
Label 6 vs Rest 4000 500 3445 Inf
Label 7 vs Rest 4000 500 3330 Inf
Label 8 vs Rest 4000 500 4000 Inf
Label 9 vs Rest 4000 500 4000 Inf
Overall 4000 500 - Inf  46.6

SVM - Results

N T SV L Acc
Train data from 1st 4000 4000 500 - Inf 22.28
Train data from 2nd 4000 4000 500 - Inf 22.24
Train data from 3rd 4000 4000 500 - Inf 46
Train data from 4th 4000 4000 500 - Inf 34.2
Train data from 5th 4000 4000 500 - Inf 41.8
Train data from 6th 4000 4000 500 - Inf 44.5

SVM - Results

Pros
1. Achieves a maximum separation of the data, i.e., "optimal separating hyper-plane"
2. It can deal with very high dimensional data.
3. Computational complexity less when compared with kNN*
4. Use of "kernel trick"**


Cons
1. *But as in our case, when number of SVs are high computational complexity increases. (when training data gets larger, number of SVs get larger)
2. **Need to select a good kernel function (should add new features so that we have a linearly separable data set from)

Two Layer Feedforward Neural Network - Setup

F.c. Layer - F.c. Layer

  • Written in Python.
  • Optimized via SGD.
  • Batch size is 100.
  • # of epoch is 200.
  • Trained/Tested on  EC2 with 32 CPUs.

Two Layer Feedforward Neural Network - Setup

Hyper Parameters Value
Regularization 1
Learning Rate 1e-5
# of Hidden Units 300
Momentum 0.98
Activation Func. ReLU
Cost Cross-entropy + reg.

F.c. Layer - F.c. Layer

Two Layer Feedforward Neural Network - Setup

Result

89.83%

Convolutional Neural Network

Conv - Pool - F.c. Layer

  • Written in MATLAB.
  • Optimized via SGD.
  • Batch size is 256.
  • # of epoch is 10.

Convolutional Neural Network

Conv - Pool - F.c. Layer

Hyper Parameters Value
Filter Width 9
Pooling Size 2x2
Learning Rate 0.1 
# of Features 20
Momentum 0.95
Activation Func. Softmax
Cost Cross ent. + Reg.

Convolutional Neural Network - Model Comparison

Kernel Width 7 9 11
Accuracy 98.2% 98.08% 98.2%
# of Kernels 14 16 18 20 22 24 26 28
Accuracy 98.4% 98.2% 98.4% 98.1% 98.3% 98.3% 98% 98.3%
Momentum 0.2 0.4 0.6 0.8 0.9 0.95
Accuracy 96.5% 96.6% 97.4% 97.9% 98% 98.5%

Best Result: 98.08%

Deep Convolutional Neural Network

Conv. - Pool - Conv. - Pool - F.c. Layer - F.c. Layer

  • Written in Torch7.
  • Optimized via SGD.
  • Batch size is 100.
  • # of epoch is 100.
  • Learning rate 0.05
  • Trained/Tested on nVIDIA GTX on EC2.

Deep Convolutional Neural Network - Activation Functions

Activation Func. Accuracy
Tanh 99.14%
ReLU 99.18%
Sigmoid 98.77%  (Takes too long!)

Deep Convolutional Neural Network - Momentum

Momentum Accuracy
0.95 99.12%
0.90 99.08%
0.98 98.84%
0102030405060708090100# epochs020406080100Test accuracyTest accuracies for different momentum values0.950.980.90

Deep Convolutional Neural Network - Dropout

Dropout Accuracy
0.2 98.86%
0.4 98.92%
0.6 97.74%

Deep Convolutional Neural Network - More Deeper Models

Activation Func. Dropout Momentum Accuracy
ReLU - - 99.15%
Tanh - - 98.97%
ReLU 0.4 - 98.84%
ReLU 0.2 - 98.86%
ReLU - .95 99.21%
ReLU - .98 99.09%

Conv. - Pool - Conv. - Pool - F.c. Layer - F.c. Layer - F.c. Layer

Deep Convolutional Neural Network - Batch Normalization

  1. In SGD , the distribution of inputs to a hidden layer will change because the hidden layer before it is constantly changing as well. This is known as covariate shift.
  2. It is known that whitened data makes learning faster.
  3. Therefore apply whitening to every layer.
(arXiv:1502.03167 [cs.LG])

Deep Convolutional Neural Network - Batch Normalization

Deep Convolutional Neural Network - Batch Normalization

Batch Normalization Accuracy
2 F.c. Layer 98.86%
3 F.c. Layer 98.85%
4 F.c. Layer (+.95 momentum) 98.79%

Deep Convolutional Neural Network - More Deeper Models

Activation Func. Dropout Momentum Accuracy
ReLU - .95 99.31%

Conv. - Pool - Conv. - Pool - F.c. Layer - F.c. Layer - F.c. Layer - F.c. Layer

Deep Convolutional Neural Network - Practical Issues

  1. For the search of the best model, one should run several different models at the same time.
  2. This requires high computing resource.
  3. GPUs are ~x10 faster than CPUs.
  4. Google's Tensorflow does not work on Amazon GPUs.
  5. Sigmoid is not useful as it is x10-15 times slower than ReLU, tanh.
  6. Dropout did not give much benefit.

Final Result

99.31\%
99.31%99.31\%

Conv - Pool - Conv - Pool - F.c Layer - F.c. Layer - F.c. Layer - F.c. Layer

 

ReLU

.95 Momentum

No Dropout

Thanks for Listening!

DeepRetina

DeepRetina Final Presentation

By Yigit Demirag

Made with Slides.com

DeepRetina Final Presentation

  • 1,306

More from Yigit Demirag