cog sci 131 section

week 04/25/22

by yuan meng

agenda

  • overview of key concepts
  • information and english 
  • hw10 prompt walkthrough

key concepts

  • surprisal of a particular outcome

 

  • information entropy: average surprisal over a set of outcomes

 

  • conditional entropy
    • one specific outcome:
    • a set of outcomes:
  • ​mutual information: reduction in entropy (a.k.a. "information gain")​
    • ​one specific outcome:
    • a set of outcomes:

 

\displaystyle{\mathrm{I}(x_i) =-\log_2 {\mathrm{P}(x_i)}}
\displaystyle{\mathrm{H}(X) = \sum_{i}^{n}\mathrm{P}(x_i)\mathrm{I}(x_i) = -\sum_{i}^{n}\mathrm{P}(x_i)\log \mathrm{P}(x_i)}
P(\square) = 1/2
P(\square) = 1/4
P({\Large{\circ}}) = 1/4
\displaystyle{\mathrm{H}(X|y)}
\mathrm{H}(X|Y) = \sum_{j}^{m}P(y_j)\mathrm{H}(X|y_j)

"is it yellow?"

"nope"

P(\mathrm{\square|blue}) = 1

"yup"

P(\mathrm{\square|blue}) = 0
-\log P(\square) = 1
-\log P(\square) =2
\log_2 P({\Large{\circ}}) = 2
\displaystyle{\mathrm{H}(X) = 1/2 \times 1 + 1/4 \times 2 + 1/4 \times 2} = 3/2
-\log_2 P(\mathrm{\square|blue}) = 0
-\log P(\mathrm{\square|blue}) \to \infty
P({\Large{\circ}}|\mathrm{blue}) = 0
-\log P({\Large{\circ}}|\mathrm{blue}) \to \infty
\mathrm{H}(X|\mathrm{blue}) = 1 \times 0 + 0 \times (-\log_2 0) + 0 \times (-\log_2 0) = 0
P(\mathrm{\square|blue}) = 0
P(\mathrm{\square|blue}) = 1/2
-\log_2 P(\mathrm{\square|blue}) \to \infty
-\log P(\mathrm{\square|blue}) = 1
P({\Large{\circ}}|\mathrm{blue}) = 1/2
-\log P({\Large{\circ}}|\mathrm{blue}) = 1
\mathrm{H}(X|\mathrm{yellow}) = 0 \times (-\log_2 0) + 1/2 \times 1 + 1/2 \times 1 =1
\mathrm{H}(X|\mathrm{color}) = 1/2 \times 0 + 1/2 \times 1 = 0.5
\displaystyle{\mathrm{H}(X) - \mathrm{H}(X|y)}
\displaystyle{\mathrm{H}(X) - \mathrm{H}(X|Y)}

to find the answer, is it cleverer to ask about shape or color?

\mathrm{H}(X|\mathrm{shape}) \approx 1/4 \times 0 + 3/4 \times 0.91 \approx 0.68

same for shape (square or circle)

color reduces more entropy!

l'hôpital's rule

insight: clever questions roughly halve the hypothesis space  

"thus twenty skillful hypotheses will ascertain what two hundred thousand stupid ones might fail to do." — charles s. pierce (1901)

get "yes" half of time and "no" also half of the time

information and english

20 questions game

  • let's play... i'll think of a noun and you can ask me at most 20 yes/no questions to guess what it is
    • what are some good questions to ask?
  • analyze theoretical limit
    • if you always ask perfect questions, how many do you need at most to get to the answer?
    • in principle, when is it impossible for a perfect question asker to find the answer?

information of english 

variation: "guess which word i'm thinking about!"

  • probability of a word: use entire vocabulary

 

 

  • "it starts with b" 👉 conditional probability of a word: use filtered vocabulary 

 

 

  • mutual information: 

data: 41,460 english words + their frequencies

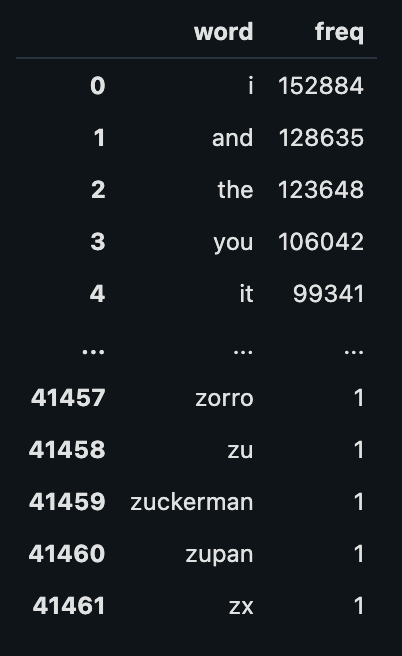
P(\mathrm{word}_i) = \frac{\mathrm{frequency}_i}{\sum_i^{n}\mathrm{frequency}_i}
word freq
amen 10
banana 100
boba 50

toy vobaculary

P(\mathrm{boba|b}) = \frac{P(\mathrm{boba})}{P(\mathrm{boba})+P(\mathrm{banana})} = \frac{\frac{50}{10+100+50}}{\frac{50}{10+100+50}+\frac{100}{10+100+50}} = \frac{50}{50+100}
P(\mathrm{word}_i|\mathrm{condition}) = \frac{\mathrm{frequency'}_i}{\sum_i^{m}\mathrm{frequency'}_i}
\mathrm{H(words)} - \mathrm{H(words|condition)}

cross out impossible row(s)

\displaystyle{\mathrm{H}(\mathrm{words}) = -\sum_{i}^{n}P(\mathrm{word}_i)\log P(\mathrm{word}_i)}

entropy of all words

\displaystyle{\mathrm{H}(\mathrm{words|condition}) = -\sum_{i}^{m} P(\mathrm{word_i|condition})\log P(\mathrm{word_i|condition})}

entropy of remaining words

most useful condition: neither too common or rare

hw10 prompts

hints & details

  1. base of log: use np.log2, not np.log
  2. missing values: "Assignment10-WordFrequencies.csv" has 2 rows with missing values 👉 can drop them
  3. not all words have vowels​ 👉 how to compute conditional probabilities and conditional entropies?
    • create a 'first_vowel' column from 'word'
    • filter rows by first_vowel
  4. useful functions: filter rows by strings in a column

 

# start with a character (e.g., char = 'b')
df[df["word"].str.startswith(char)]
# end with a character
df[df["word"].str.endswith(char)]
# first vowel (e.g., vowel = 'a')
df[df["first_vowel"] == vowel]

entropy conditioned on first character

homework 10, q4

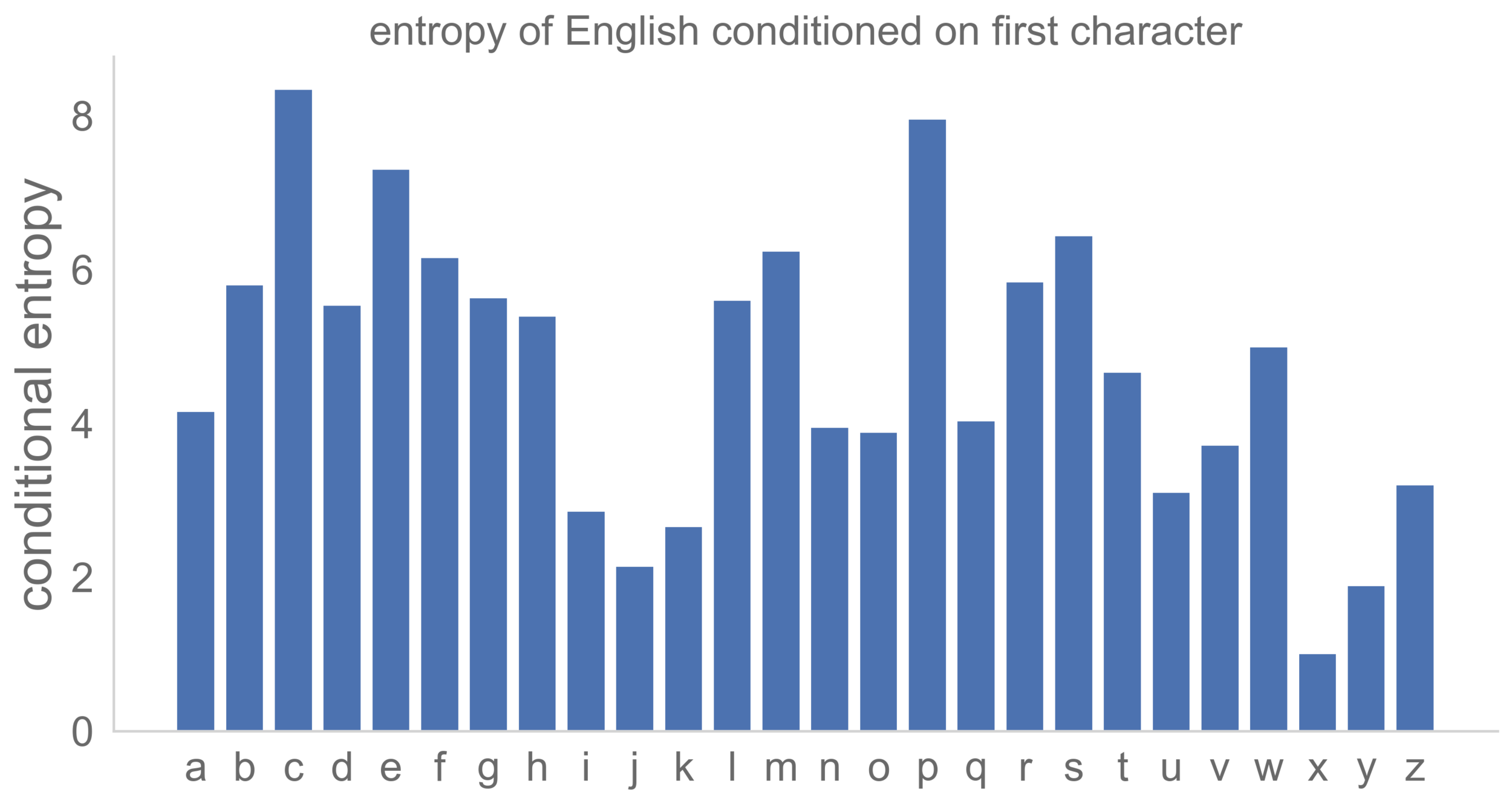
more info on info theory

david mackay's "bible" (website)

cogsci131_04_25

By Yuan Meng

cogsci131_04_25

  • 150

More from Yuan Meng