teaching a perceptron to see
first course in deep learning
by yuan meng
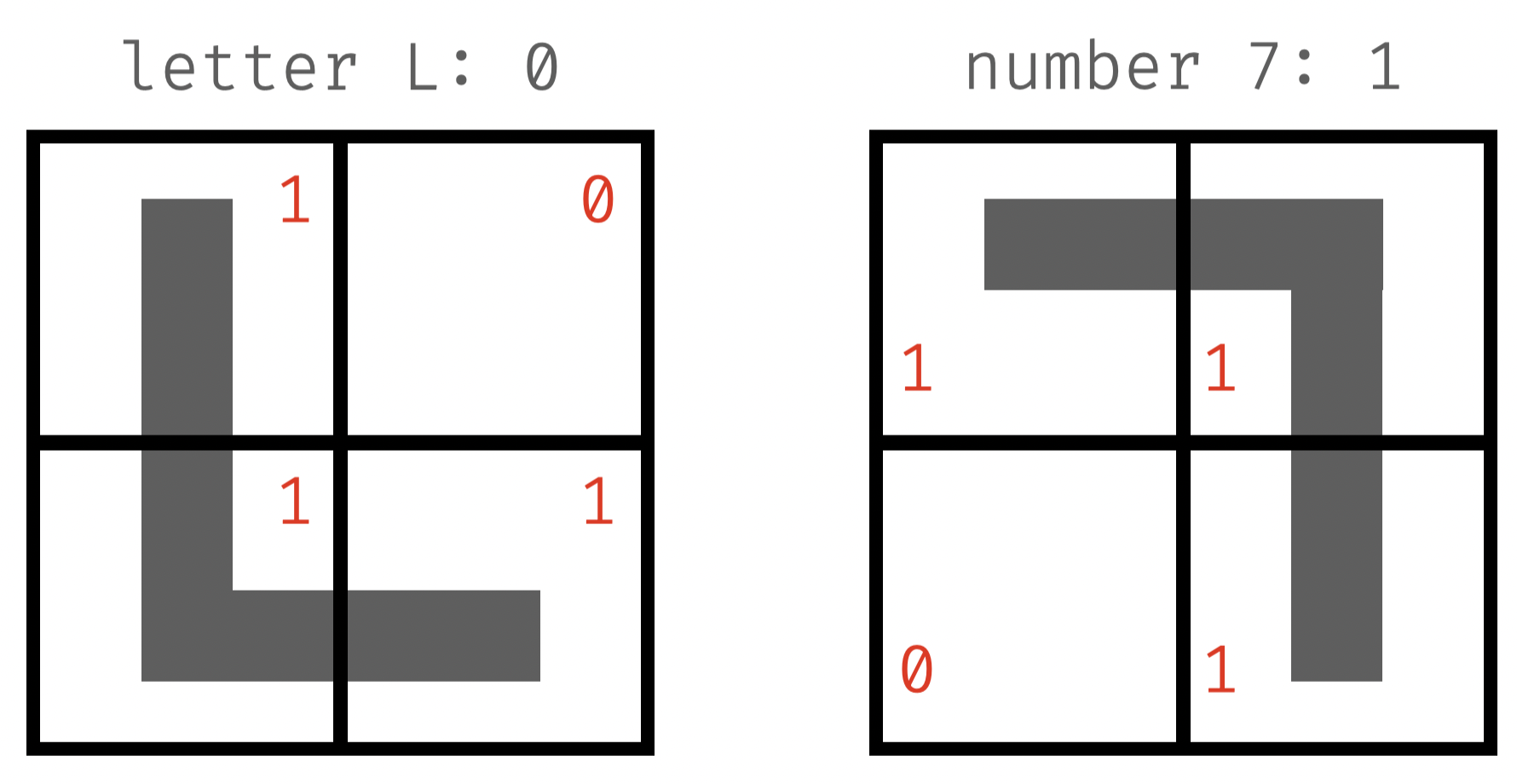
how do we tell apart L vs. 7? 👀
-
describe your thoughts in plain english
- "L": top right is empty (0) + lower left is not empty (1)
- "7": lower left is empty (0) + top right is not empty (1)

vs.
but how does a machine see?
-
map pixel values into class labels (0 for L vs. 1 for 7)
- x: a vector encoding the value of each pixel 👉 known
- w: a vector encoding the weight of each pixel 👉 unknown
- sign of dot product (
np.dot(x, w)) determines label


vs.
class label: 0
class label: 1
X: [1, 0, 1, 1]
X: [1, 1, 1, 0]
w: [?, ?, ?, ?]
w: [?, ?, ?, ?]
\mathbf{w}^T \mathbf{x} < 0
\mathbf{w}^T \mathbf{x} > 0
how do we know the weights?


vs.
class label: 0
class label: 1
X: [1, 0, 1, 1]
X: [1, 1, 1, 0]
w: [0, -, 0, -]
w: [0, +, 0, +]
\mathbf{w}\cdot\mathbf{x} < 0
\mathbf{w}\cdot\mathbf{x} > 0
- "hand-pick" weights to get desired results
- pixels 1 & 3 not pulling punches 👉 0
-
pixels 2 & 4 👉 same direction as
np.dot(x, w)
- start with random weights 👉 learn from errors
learn to classify L vs. 7
- initialization: start with random weights, w = [0.5, 0.9, -0.3, 0.5]
-
training: "see" an example of "L"
- dot product > 0 👉 classify as "7"
- wrong❗️updating is needed
-
update: increase or decrease w?
- decrease! because dot product is too big (should be < 0)
- how to decrease (one possible method): subtract x from w

\mathbf{w}^T \mathbf{x} = 0.5 \times 1 + 0.9 \times 0 -0.3 \times 1 + 0.5 \times 1 = 0.7
class label: 0
\mathbf{w}-\mathbf{x} \\ = [0.5 - 1, 0.9 - 0, -0.3 - 1, 0.5 - 1] \\ = [-0.5, 0.9, -1.3, -0.5]
try again!
- new weights: [-0.5, 0.9, -1.3, -0.5]
-
training: "see" an example of "7"
- dot product < 0 👉 classify as "L"
- wrong❗️updating is again needed
-
update: increase or decrease w?
- increase! because dot product is too small (should be > 0)
- new weights: add x to w

\mathbf{w}^T \mathbf{x} = -0.5 \times 1 + 0.9 \times 1 -1.3 \times 0 - 0.5 \times 1 = -0.1
class label: 1
\mathbf{w}-\mathbf{x} \\ = [-0.5 + 1, 0.9 + 1, -1.3 + 0, - 0.5 + 1] \\ = [0.5, 1.9, -1.3, 0.5]

learn to classify L vs. 7
here we go again
classify L vs. 7
- new weights: [0.5, 1.9, -1.3, 0.5]
-
training: "see" an example of "L"
- dot product < 0 👉 classify as "L"
- correct❗️no need to update
-
neural nets usually train on more than 3 examples...
- in order to achieve good performance
- 👉 evaluation metrics: accuracy (# of correct/# test cases), precision (actually L/say L), recall (say L/actually L), log-loss...
- early stop when improvement stalls
- in order to achieve good performance

\mathbf{w}^T \mathbf{x} = 0.5 \times 1 + 1.9 \times 0 -1.3 \times 1 + 0.5 \times 1 = -0.3
class label: 0
🥳
implement perceptron from scratch to classify hand-written digits
dl 101: teaching a perceptron to see
By Yuan Meng
dl 101: teaching a perceptron to see
- 156



