圖論3
yungyao
主題
- DFS Tree
- 關節點
- 橋
- BCC
- 有向圖
- DAG
- SCC
- 2-SAT
前言
- 沒有特別註明下,圖都是無向簡單連通圖(無重邊、自環)
- 你等一下會看到很多Tarjan
- 做這份簡報的人很弱
也可以看看別人的Slides
用8wcp認識圖論
IOI 2022 Gold Medalist C. Liu (2021)
DFS Tree
把dfs過程記錄起來
無向圖上
- Tree Edge
- Back Edge
小結
把邊分成在DFS Tree上的Tree Edge以及不在的Back Edge
對於在DFS時訪問到新節點的邊設為Tree Edge
往已經訪問過的節點則設為Back Edge
- Back Edge一定通往祖先
- Tree Edge會有恰 \(V - 1\) 條邊
- 有向圖上還有Cross Edge跟Forward Edge,今天不討論
關節點
拔掉一個人的關節,他就會死
什麼是關節點
關節點!
關節點定義
拔掉該點後,圖會變得不連通
如何找
在DFS Tree上做事!
維護兩個個函式 \(low\) 及 \(dep\)
\(low(x)\) 表示由 \(x\) 開始往子孫走
再經由至多一條Back Edge能走到的最淺深度
\(dep\) 則代表在DFS Tree上的深度
1
9
8
7
6
5
4
3
2
\(dep = 1\)
\(dep = 2\)
\(dep = 3\)
\(dep = 4\)
\(low(2) = 1\)
\(low(3) = 1\)
\(low(4) = 4\)
\(low(1) = 1\)
\(low(5) = 1\)
\(low(6) = 1\)
\(low(7) = 1\)
\(low(8) = 2\)
\(low(9) = 2\)
然後呢?
在DFS Tree上的節點 \(u\)
- 是根節點,且有至少兩個子節點
- 不是根節點,且至少存在一子節點\(x\text{ } s.t. low(x) \geq dep(u)\)
就是關節點
實作
利用樹DP
vector <int> adj[maxn];
int dep[maxn], low[maxn];
bool vis[maxn];
vector <int> ap_list;
void dfs(int x, int fr = 0){ //int fr = 0 表示在沒有傳入值下預設為 0
low[x] = dep[x] = dep[fr] + 1; //初始化數值
vis[x] = true;
int c = 0;
bool flag = true;
for (auto i:adj[x]) if (i != fr){
if (vis[i]) low[x] = min(low[x], dep[i]); //遇到Back Edge,更新low
else{
++c;
dfs(i, x); //遇到Tree Edge,向下dfs
low[x] = min(low[x], low[i]); //更新low
if (fr and low[i] >= dep[x] and flag){ //遇到子節點low值大於等於x的深度
flag = false;//注意不要重複設置關節點
ap_list.pb(x);
}
}
}
if (!fr and c > 1) ap_list.pb(x); //特判根節點的case
}
題目
橋/BCC
跟關節點差不多
什麼是橋
橋!
橋定義
拔掉該邊後,圖會變得不連通
如何找
在DFS Tree上做事!
維護兩個個函式 \(low\) 及 \(dep\)
\(low(x)\) 表示由 \(x\) 開始往子孫走
再經由至多一條Back Edge能走到的最淺深度
\(dep\) 則代表在DFS Tree上的深度
跟關節點一樣!

然後呢?
- Back Edge不會是橋(Back Edge必定在環上)
- 對於每條Tree Edge所連結較深的那個點 \(x\)
- 若 \(low(x) \geq dep(x)\) 則該邊為橋
邊雙連通/橋連通 分量 (BCC)
邊雙連通:任兩點間都存在至少兩條簡單路徑
邊雙連通分量,意指把圖分成好幾個邊雙連通的分量
Tarjan's BCC Algorithm
用一個stack紀錄dfs序
遇到橋時,把所有 stack 內 \(x\) 以上的點放入目前的分量
\(x\) 的子樹內的點不屬於其他分量的點,都屬於這個新的分量
實作
vector <int> adj[maxn];
int bcccnt = 0;
int bl[maxn], dep[maxn], low[maxn];
bool vis[maxn];
stack <int, vector<int>> dfsr;
void dfs(int x, int fr){
dfsr.push(x);
for (auto &i:adj[x]) if (i != fr){
if (vis[i]) low[x] = min(low[x], dep[i]);
else{
dfs(i, x);
low[x] = min(low[x], low[i]);
}
}
if (low[x] == dep[x]){
++bcccnt;
int k;
do{
k = dfsr.top(); dfsr.pop();
bl[k] = bcccnt;
}while (k != x);
}
}
要幹嘛?
可以觀察到,把連通分量縮成一個點之後
剩下來的邊都是橋
\(\Rightarrow\) 會形成一棵樹
於是我們就可以把一般圖上的問題轉到樹上了
偷圖
Credit:奇怪的中國網站
題目
套到關節點上?
套到關節點上會形成點雙連通分量和圓方樹
但她好難,我們不要理他
我去年講過ㄌ,好欸少做一份簡報
SCC
強強的連通分量
Strongly Connected Component (SCC)
強連通表示對於所有節點對 \((a, b)\)
都同時存在 \(a\) 到 \(b\) 和 \(b\) 到 \(a\) 的路徑
DFS序/時間戳記
在dfs的過程中,紀錄進入/離開節點的順序
兩個算法
- Kosaraju
- 常數稍差,簡單好寫
- Tarjan's SCC
- 常數小,難一點
複雜度都是線性 \(O(n+m)\)
Kosaraju's Algorithm
在原圖外,額外存一張由反向的邊組成的反圖
Kosaraju's Algorithm
- 先在正圖上dfs,紀錄離開順序
- 依離開順序,做為起點在反圖上dfs
- 在每次反圖上的dfs中被新遍歷到的點屬於一個SCC
證明
我們可以由定義知道若在正圖和反圖上都可以從 \(a\) 走到 \(b\)
則 \(a, b\) 屬於同一SCC
我們也可以觀察到,stack 頂端的點屬於的SCC入度必為0
也就是在反圖上的出度為0
因此每次反圖上所走到的節點必屬於同一SCC
而把這些點拔除後剩下的圖會有一樣的性質
我們就可以用數歸證明Kosaraju的正確性了
\(Q. E. D.\)
Tarjan's SCC
繼續做 \(low\) 函式
但存的是 DFS 進入序
且我們只用目前還在 stack 內的點去更新 \(low\)
Tarjan's SCC
如果遇到一個點 \(x \text{ s.t. } low(x) = time\_stamp(x)\)
則我們將 stack 中 \(x\) 以上的點都丟入一個新的SCC
證明
The proof is left as an exercise for the reader.(X
所以SCC要幹嘛?
邊雙連通分量把圖變成樹
那SCC呢?
變成DAG!
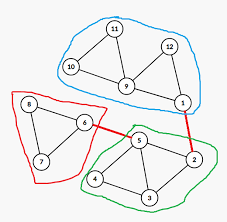
這裡有一張圖,著相同顏色的屬於同一SCC
縮成一張DAG了!
Credit: FHVirus's Slides
題目
(這題也有不用SCC的解)
2-SAT
學會2-SAT了,來試試看3-SAT怎麼做吧
Boolean Satisfiability Problem
資芽仔應該都聽過ㄌ,幫我講(X
我們定義 Clause 為一個或多個布林變數取正或取反的 OR 和
而若將多個 Clause 取AND
並且詢問是否存在一組解使整個表達式為 TRUE
即為一個 SAT-problem
(a or b or c) and (!a or !d or e) and (d or !e)一個SAT問題
2-SAT
2-SAT為一SAT問題的特例
也就是每個 Clause 只會由恰兩個變數組成
(a or b) and (!b or c) and (b or d) and (!c or !d)一個2-SAT問題
2-SAT 作法
我們可以對於每個布林變數維護兩個節點
分別代表其取True或False
而對於一個2-Clause,我們可以用兩條邊
分別表示一個值取特定值後另一變數必須取特定值
如果存在一個點取正取反都在同一SCC內則無解
否則按照反圖上的拓樸排序取值!
The proof is left as an exercise for readers(X
題目
圖論3
By yungyao
圖論3
- 290



