Knowledge-Injected
Federated Learning
Zhenan Fan
Huawei Technologies Canada
Midwest Optimization Meeting 2022
Collaborators:
Zirui Zhou, Jian Pei, Michael P. Friedlander,
Jiajie Hu, Chengliang Li, Yong Zhang
Outline
1
Motivating Case Study
Knowledge-Injected Federated Learning
Numerical Results
2
3
Coal to Make Coke and Steel

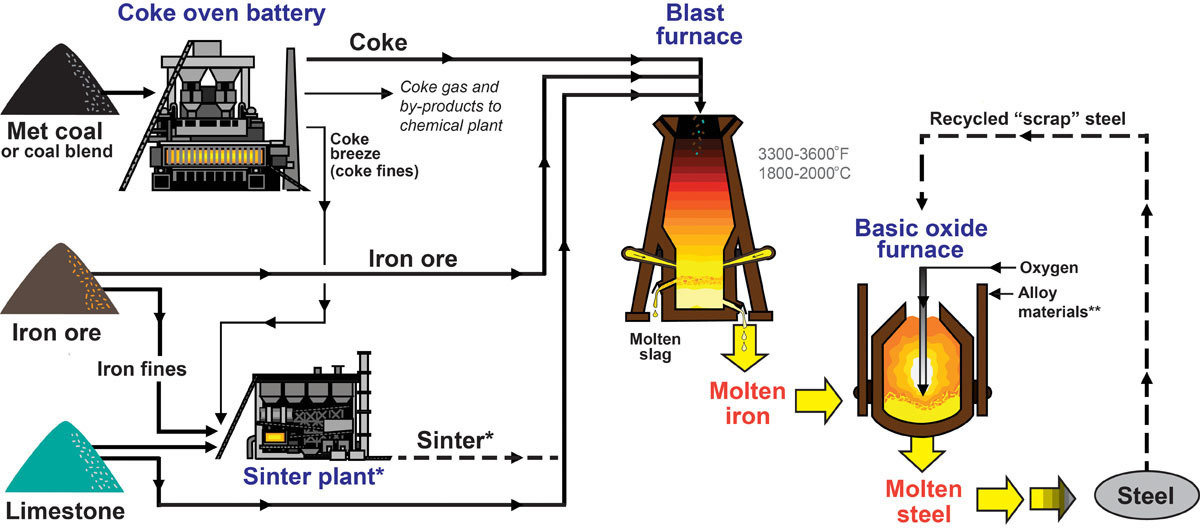
https://www.uky.edu/KGS/coal/coal-for-cokesteel.php
Coal-Mixing in Coking Process

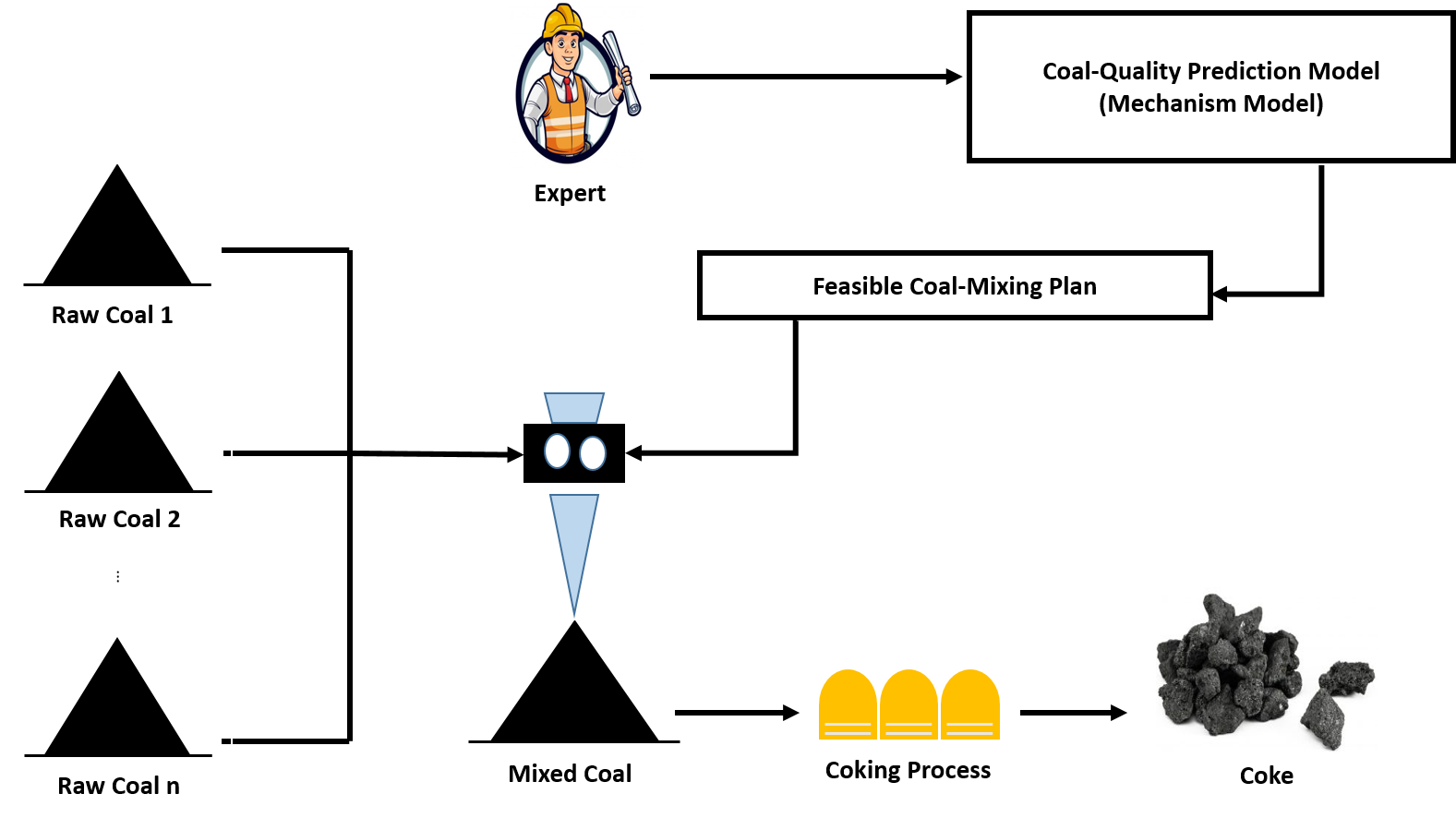
Challenging as no direct formula
Based on experience and knowledge
largely affects cost

Task Description
Goal: improve the expert's prediction model with machine learning
Data scarcity: collecting data is expensive and time consuming
We unite 4 coking industries to collaboratively work on this task
Challeges
local datasets have different distributions
industries have different expert(knowledge) models
privacy of local datasets and knowledge models has to be preserved
Multiclass Classification

\red{\mathcal{D}} = \left\{(\blue{x^{(i)}}, \green{y^{(i)}}\right\}_{i=1}^N \subset \blue{\mathcal{X}} \times \green{\{1,\dots,k\}} \sim \purple{\mathcal{F}}
training set
data instance
(features of raw coal)
feature space
label
(quality of the final coke)
label space
data distribution
Task
\text{Find}\enspace
f: \mathcal{X} \to \{1,\dots,k\}
\enspace\text{such that}\enspace
\mathop{\mathbb{E}}_{(x,y)\sim\mathcal{F}}[f(x) \neq y]
\enspace\text{is small.}
Setting
\enspace\text{or}\enspace
\mathop{\mathbb{E}}_{(x,y)\sim\mathcal{D}}[f(x) \neq y]
\enspace\text{is small.}
Knowledge-based Models

Prediction-type Knowledge Model (P-KM)
g_p: \mathcal{X} \to \{1,\dots,k\}
\enspace\text{such that}\enspace
g_p(x)
\enspace\text{is a point estimation for}\enspace
y
\enspace\forall (x,y) \sim \mathcal{F}
Range-type Knowledge Model (R-KM)
g_r: \mathcal{X} \to 2^{\{1,\dots,k\}}
\enspace\text{such that}\enspace
y \subseteq g_r(x)
\enspace\forall (x,y) \sim \mathcal{F}
Eg. Mechanistic prediction models, such as an differential equation that describes the underlying physical process.
Eg. Can be derived from the causality of the input-output relationship.
\red{(k = 3,\enspace g_p(x) = 2)}
\red{(k = 3,\enspace g_r(x) = \{2, 3\})}
Federated Learning with Knowledge-based Models

M clients and a central server.
\text{training set}\enspace
\mathcal{D}^m \sim \purple{\mathcal{F}^m}
conditional data distribution depending on
\text{P-KM}\enspace
g_p^m
\enspace\text{for distribution}\enspace
\mathcal{F}^m
\text{R-KM}\enspace
g_r^m
\enspace\text{for distribution}\enspace
\mathcal{F}^m
\purple{\mathcal{F}}
Each client m has
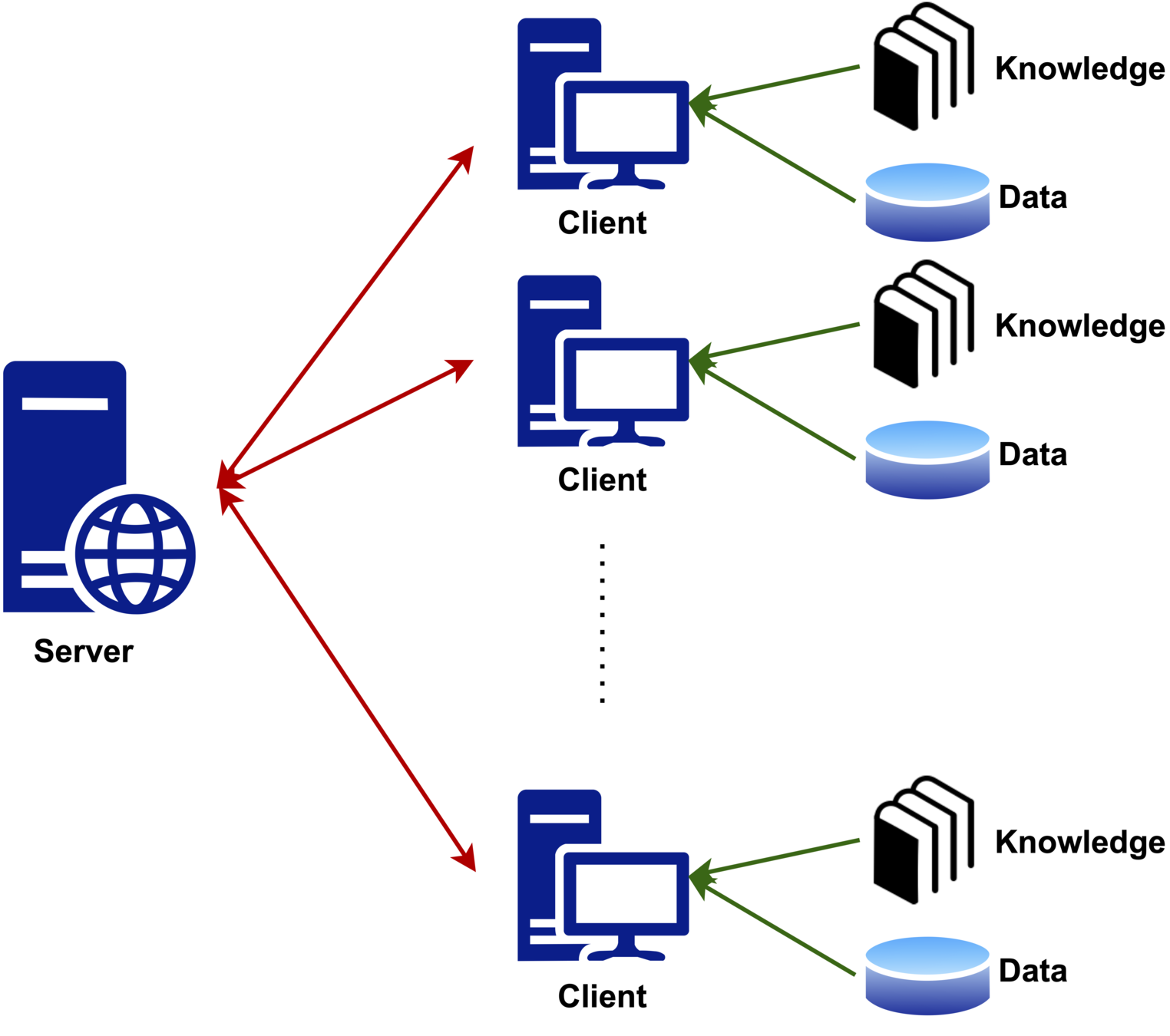
g_p^m
\enspace\text{agrees with}\enspace
g_r^m
\enspace \red{(g_p^m(x) \in g_r^m(x) \enspace \forall x)}
Task Description

each client m obatins a personalized predictive model
f^m: \mathcal{X} \to \Delta^k \coloneqq \{p \in \mathbb{R}^k \mid \sum p_i = 1\}
f^m \enspace\text{utilize the local P-KM}\enspace g^m_p \enspace\text{with controllable trust level}
f^m \enspace\text{agrees with local R-KM}\enspace g^m_p
\enspace\text{i.e.}\enspace
\{i \mid f^m(x)_i > 0\} \subseteq g^m_r(x)\enspace
\forall x \in \mathcal{X}
Design a federated learning framework such that
clients can benefit from others' datasets and knowledge
privacy of local datasets and local KMs needs to be protected
Direct Formulation Invokes Infinitely Many Constraints

Simple setting
\text{Single client with}\enspace \mathcal{X} = \mathbb{R}^d
\text{Logistic model}\enspace f(\theta; x) = \blue{\mathop{softmax}}(\theta^T x) \enspace\text{with}\enspace \theta\in\mathbb{R}^{d\times k}
\blue{
\mathop{softmax}(z \in \mathbb{R}^k)_i = \dfrac{\exp(z_i)}{\sum_j \exp(z_j)}
}
\red{(f(\theta; \cdot): \mathbb{R}^d \to \Delta^k)}
\text{Loss function}\enspace \mathcal{L}(\theta) = \frac{1}{|\mathcal{D}|} \sum\limits_{(x,y) \in \mathcal{D}}
\blue{\mathop{crossentropy}}(f(\theta; x), y)
\blue{
\mathop{crossentropy}(p\in\Delta^k, y\in\{1,\dots,k\}) = -\log(p_y)
}
Challenging optimization problem
\min\limits_{\theta \in \mathbb{R}^{d\times k}} \enspace
\mathcal{L}(\theta)
\enspace\text{s.t.}\enspace
\{i \mid f(\theta; x)_i > 0\} \subseteq g_r(x)
\enspace \forall x \in \mathbb{R}^d
\red{(\text{infinitely many constraints})}
Architecture Design

The server provides a general deep learning model
f(\red{\theta}; \cdot): \mathcal{X} \to \mathbb{R}^k
learnable model parameters
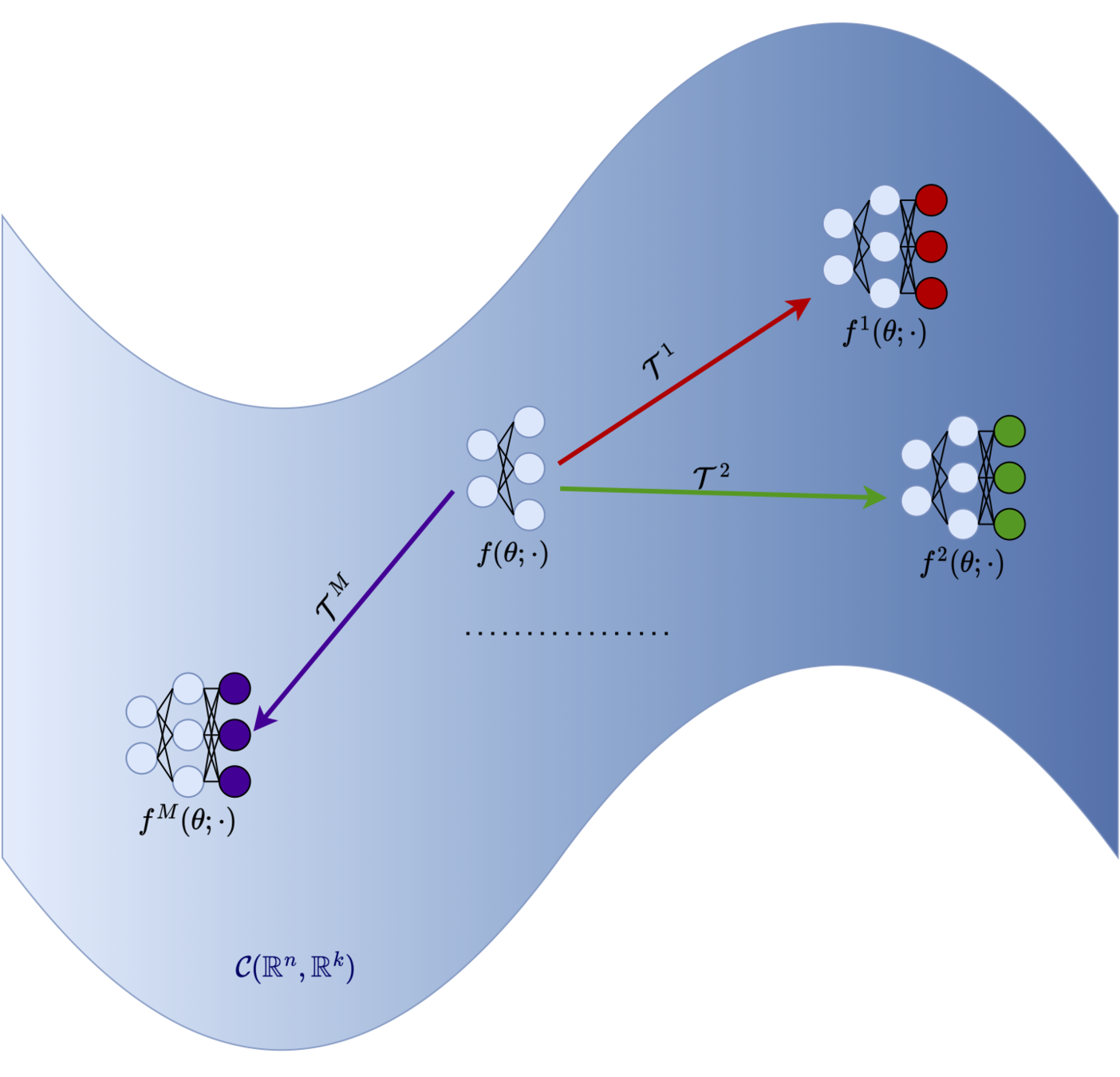
Function transformation
\mathcal{T}_{\lambda, g_p, g_r}(f)(x) =
(1-\lambda)\mathop{softmax}(f(x) + z_r) + \lambda z_p
where
(z_r)_i =
\begin{cases}
0 &\text{if}\enspace i \in g_r(x)\\
-\infty &\text{otherwise}
\end{cases}
\enspace\text{and}\enspace
(z_p)_i =
\begin{cases}
1 &\text{if}\enspace i = g_p(x)\\
0 &\text{otherwise}
\end{cases}
Personalized model
f^m(\red{\theta}; \cdot) \coloneqq \mathcal{T}_{\lambda^m, g_p^m, g_r^m}(f(\red{\theta}; \cdot))
Properties of Personalized Model

f^m(\theta; \cdot)
\enspace\text{is a valid predictive model, i.e.,}\enspace
f^m(\theta; x) \in \Delta^k \enspace \forall x \in \mathcal{X}
\lambda^m \in [0,1]
\enspace\text{controls the trust-level of the local P-KM}\enspace
g^m_p
\langle f^m(\theta; x), g^m_p(x) \rangle \geq \lambda^m \enspace \forall x \in \mathcal{X}
\text{If}\enspace \lambda^m > 0.5
\enspace\text{then}\enspace
f^m
\enspace\text{coincides with}\enspace
g^m_p
\argmax_i f^m(\theta; x) = g_p^m(x)
f^m(\theta; \cdot)
\enspace\text{agrees with local R-KM}\enspace
g^m_r
\{i \mid f^m(x)_i > 0\} \subseteq g^m_r(x)\enspace
\forall x \in \mathcal{X}
Optimization

Optimization problem
\min\limits_{\theta}\enspace\red{\mathcal{L}}(\theta) \coloneqq \sum\limits_{i=1}^M \red{\mathcal{L}^m}(\theta)
\enspace\text{with}\enspace
\mathcal{L}^m(\theta) = \frac{1}{|\mathcal{D}^m|}\sum\limits_{(x,y) \in \mathcal{D}^m} \mathop{crossentropy}(f^m(\theta; x), y)
FedAvg [McMahan et al.'17]
\text{server select a subset of clients}\enspace S \subseteq \{1,\dots,M\}
\enspace\text{and send them latest model}\enspace
\theta
\text{each selected client}\enspace m
\enspace\text{locally updates model}\enspace
\theta^m \leftarrow \theta^m - \eta\nabla\mathcal{L}^m(\theta)
\enspace (\text{d times})
\text{server updates global model by aggregating local models}\enspace
\theta \leftarrow \frac{1}{|S|}\sum\limits_{m\in S} \theta^m
global loss
local loss
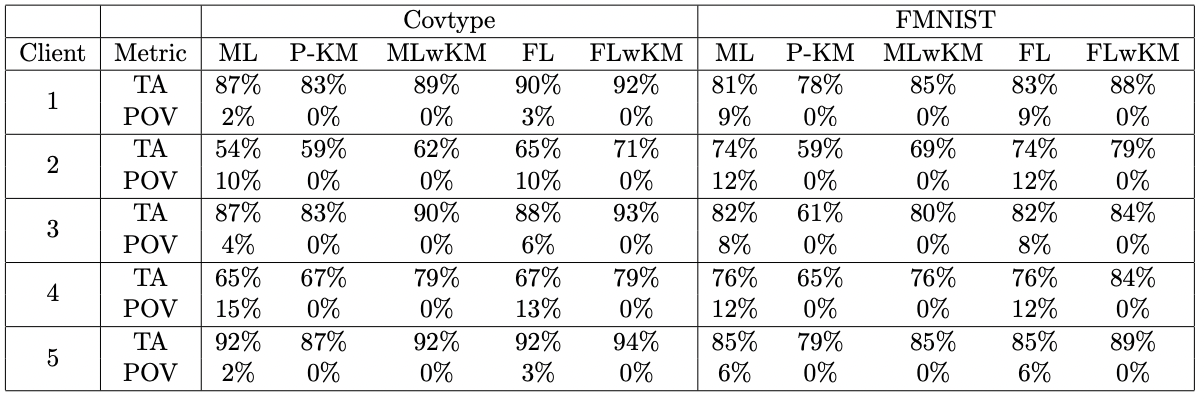
Numerical Results (Case-study)


Test accuracy
\text{TA} = \frac{1}{|\mathcal{D}^m_{\text{test}}|} \sum\limits_{(x,y) \in \mathcal{D}^m_{\text{test}}} \mathbb{I}(\{f^m(\theta; x) = y\})
Percentage of violation
\text{POV} = \frac{1}{|\mathcal{D}^m_{\text{test}}|} \sum\limits_{(x,y) \in \mathcal{D}^m_{\text{test}}}
\mathbb{I}(\{f^m(\theta; x) \notin g_r^m(x)\})
Numerical Results (Public Datasets)

Datasets
\textbf{Covtype:}\enspace
\text{number of classes}\enspace k = 7,\enspace
\text{feature space}\enspace \mathcal{X} = \mathbb{R}^{54}
\textbf{FMNIST:}\enspace
\text{number of classes}\enspace k = 10,\enspace
\text{feature space}\enspace \mathcal{X} = \mathbb{R}^{28\times 28}
Data distribution
Each client only gets samples from some classes.
P-KM
We train a deep model with a subset of features.
R-KM
We construct a hashmap to guarantee the true label is within the range.
Numerical Results (Public Datasets)

Open-source Package https: //github.com/ZhenanFanUBC/FedMech.jl
Paper Fan, Zhenan, Zirui Zhou, Jian Pei, Michael P. Friedlander, Jiajie Hu, Chengliang Li, and Yong Zhang. "Knowledge-Injected Federated Learning." arXiv preprint arXiv:2208.07530 (2022).
Thank you! Questions?
Knowledge Injected Federated Learning
By Zhenan Fan
Knowledge Injected Federated Learning
Slides for the talk at the 24th Midwest Optimization Meeting https://www.math.uwaterloo.ca/~hwolkowi/Univ.Waterloo.24thMidwestOptimizationMeeting.html
- 567



