Contribution Valuation
In
Federated Learning
Zhenan Fan
Department of Computer Science
Collaborators:
Huang Fang, Zirui Zhou, Yong Zhang, Jian Pei, Michael Friedlander

Contribution Valuation
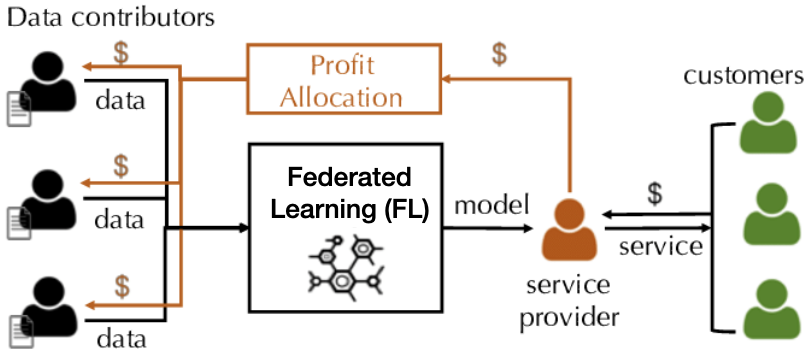
Key requirement
1. Data owners with similar data should receive similar valuation. 2. Data owners with unrelated data should receive low valuation.

Shapley Value
Shapley value is a measure for players' contribution in a game.
Advantage
It satisfies many desired fairness axioms.
Drawback
Computing utilities requires retraining the model.
performance of the model
v(\red{i}) = \frac{1}{N} \sum\limits_{S \subseteq [N] \setminus \{i\}} \frac{1}{ N-1 \choose |S|}
[U(S \cup \{i\}) - \blue{U(S)}]
player i
utility created by players in S
marginal utility gain

Federated Shapley Value
[Wang et al.'20] propose to compute Shapley value in each communication round, which eliminates the requirement of retraining the model.
v_t(i) = \frac{1}{M} \sum\limits_{S \subseteq [M] \setminus \{i\}} \frac{1}{ M-1 \choose |S|}
[U_t(S \cup \{i\}) - U_t(S)]
v(i) = \sum\limits_{t=1}^T v_t(i)
Fairness
Symmetry
U_t(S\cup\{i\}) = U_t(S\cup\{j\}) \quad \forall t, S
\Rightarrow
v(i) = v(j)
Zero contribution
U_t(S\cup\{i\}) = U_t(S) \quad \forall t, S
\Rightarrow
v(i) = 0
Addivity
U_t = U^1_t + U^2_t
\Rightarrow
v(i) = v^1(i) + v^2(i)

Horizontal Federated Learning
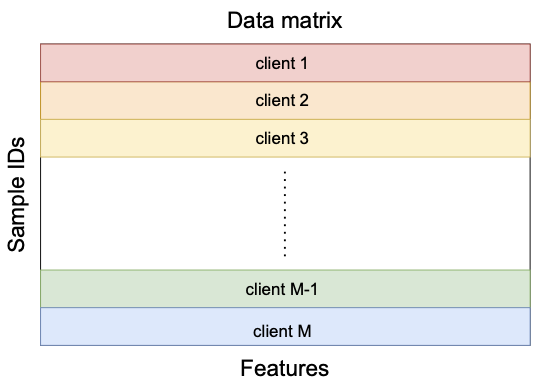
\mathop{min}\limits_{w \in \mathbb{R}^d}\enspace F(\red{w}) \coloneqq \sum\limits_{i=1}^\blue{M} f_i(w)
\enspace\text{with}\enspace
f_i(w) \coloneqq \frac{1}{|\mathcal{D}_i|} \sum\limits_{(x, y) \in \green{\mathcal{D}_i} } \purple{\ell}(w; x, y)
model
number of clients
local dataset
loss function

FedAvg
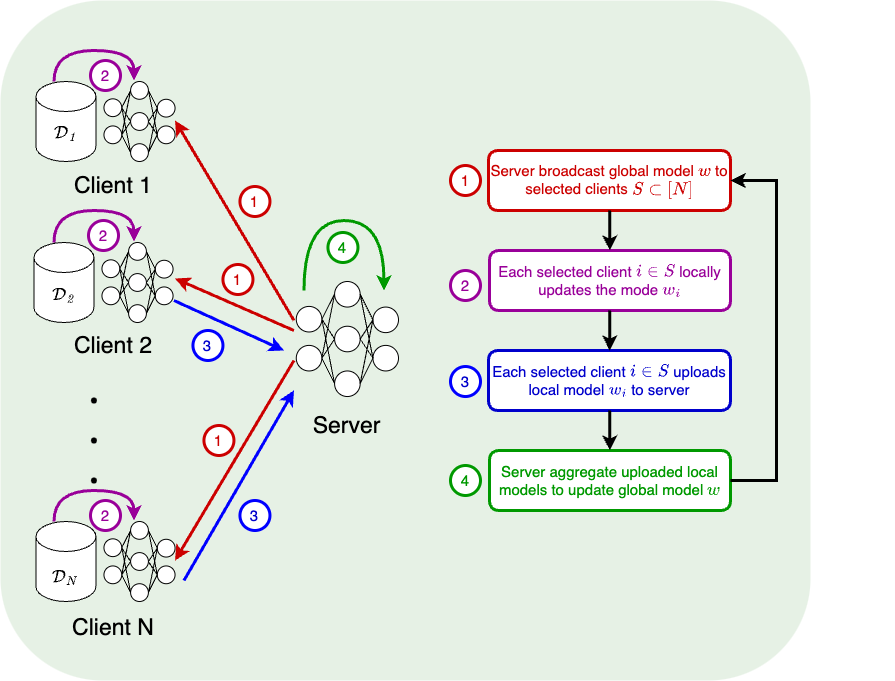
[McMahan et al.'17]
w_i^{t+1} \leftarrow w_i^t - \eta \tilde \nabla f_i(w_i^t) \quad (K \text{ times})
w^{t+1} \leftarrow \frac{1}{|S^t|}\sum_{i \in S^t} w_i^{t+1}

Utility Function
Test data set (server)
\mathcal{D}_c
U_t(S) = \sum\limits_{(x, y) \in \mathcal{D}_c} \left[ \ell(w^t; x,y) - \ell(w_S^{t+1}; x,y) \right]
\enspace\text{where}\enspace
w_S^{t+1} = \frac{1}{|S|} \sum\limits_{i \in S} w_i^{t+1}
v_t(i) =
\begin{cases}
\frac{1}{|S^t|} \sum\limits_{S \subseteq S^t \setminus\{i\}} \frac{1}{\binom{|S^t|-1}{|S|}} \left[U_t(S\cup\{i\}) - U_t(S)\right] & i \in S^t \\
0 & i \notin S^t
\end{cases}
Problem: In round t, the server only has
\{w_i^{t+1}\}_{i \in S^t}
[Wang et al.'20]

Possible Unfairness
Clients with identical local datasets may receive very different valuations.
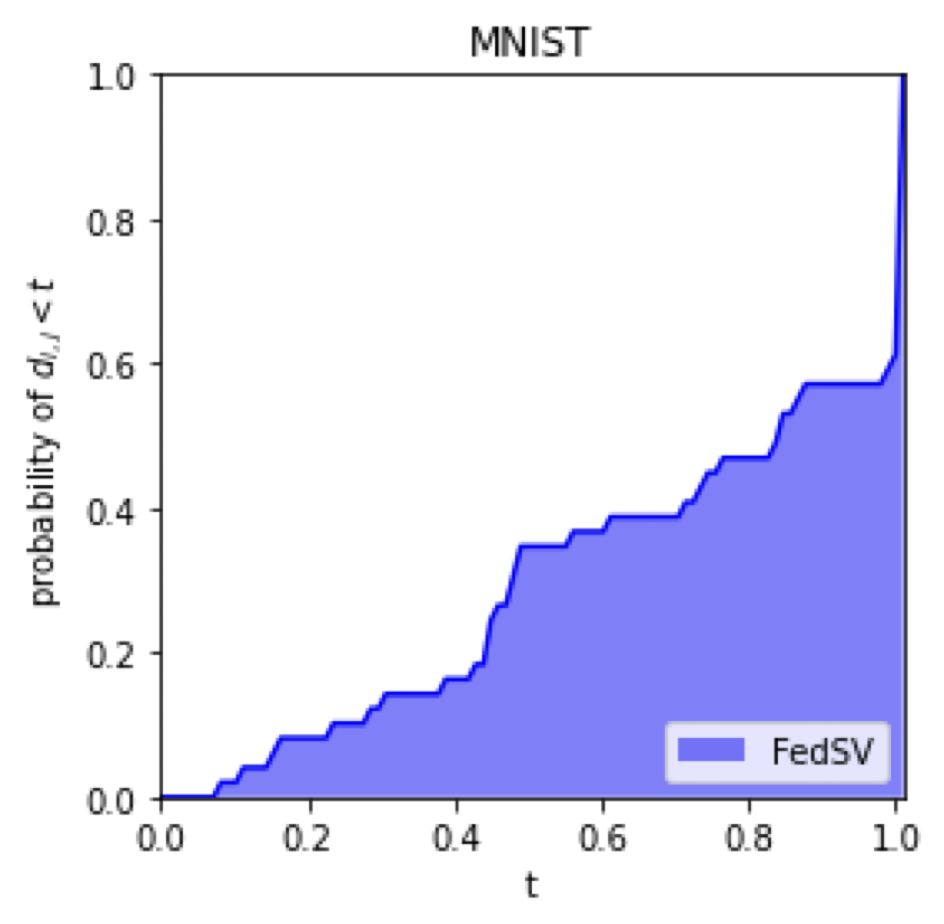
Same local datasets
\mathcal{D}_i = \mathcal{D}_j
Relative difference
d_{i,j} = \frac{|v(i) - v(j)|}{\max\{v(i), v(j)\}}
Empirical probability
\mathbb{P}( d_{i,j} > 0.5) > 65\% \quad \red{\text{unfair!}}

Low Rank Utility Matrix
Utility matrix
\mathcal{U} \in \mathbb{R}^{T \times 2^M} \enspace\text{with}\enspace \mathcal{U}_{t, S} = U_t(S)
This matrix is only partially observed and we can do fair valuation if we can recover the missing values.
Theorem
If the loss function is smooth and strong convex, then
\red{\mathop{rank}_\epsilon}(\mathcal{U}) \in \mathcal{O}(\frac{\log(T)}{\epsilon})
[Fan et al.'22]
\red{ \mathop{rank}_\epsilon(X) = \min\{\mathop{rank}(Z) \mid \|Z - X\|_{\max} \leq \epsilon\} }
[Udell & Townsend'19]

Empirical Results: Singular Value Decomposition
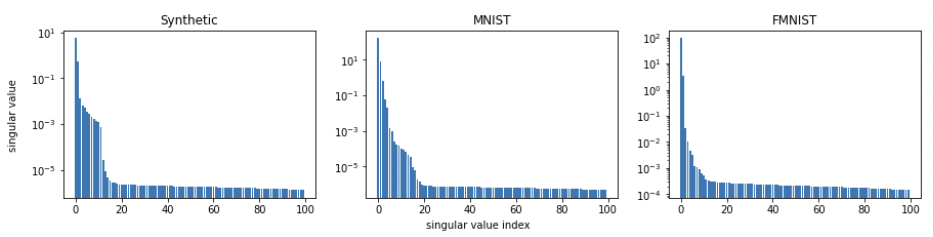

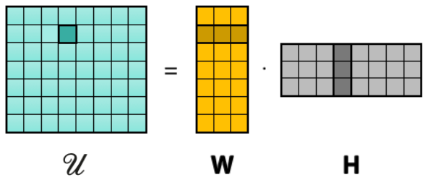
Matrix Completion
\min\limits_{\substack{W \in \mathbb{R}^{T \times r}\\ H \in \mathbb{R}^{2^N \times r}}} \enspace \sum_{t=1}^T\sum_{S\subseteq S^t} (\mathcal{U}_{t,S} - w_t^Th_{S})^2 +
\lambda(\|W\|_F^2 + \|H\|_F^2)

Same local datasets
\mathcal{D}_i = \mathcal{D}_j
Relative difference
d_{i,j} = \frac{|v(i) - v(j)|}{\max\{v(i), v(j)\}}
Empirical CDF
\mathbb{P}( d_{i,j} < t)

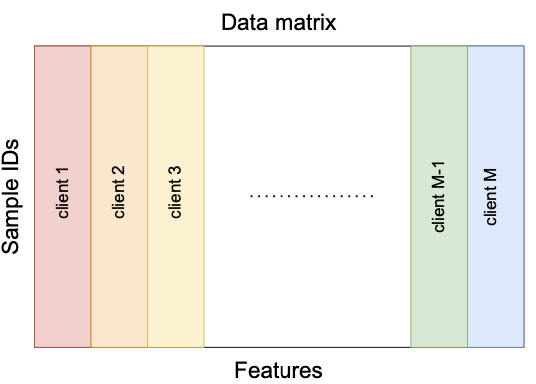
\mathop{min}\limits_{\theta_1, \dots, \theta_M}\enspace F(\red{\theta_1, \dots, \theta_M}) \coloneqq
\frac{1}{N}\sum\limits_{i=1}^{\red{N}} \ell(\sum_{m=1}^M h^m_i; y_i)
\enspace\text{with}\enspace
\blue{h^m_i} = \langle \theta_m, x_i^m \rangle
local models
local embeddings
number of training samplesOnly embeddings will be communicated between server and clients.

FedBCD
[Liu et al.'22]
Server selects a mini-batch
B^t \subseteq [N]
Each client m compute local embeddings
\{ (h_i^m)^t = \langle \theta_m^t, x_i^m \rangle \mid i \in B^t \}
Server computes gradient
\{g_i^t = \frac{\partial \ell(h_i^t; y_i)}{\partial h_i^t} \mid i \in B^t\}
Each client m updates local model
\theta_m^{t+1} \leftarrow \theta_m^t - \frac{\eta^t}{|B^t|} \sum\limits_{i \in B^t} g_i^t x_i^m


Utility Function
U_t(S) = \frac{1}{N}\sum\limits_{i=1}^N \ell\bigg(\sum\limits_{m=1}^M (h^m_i)^{t-1}; y_i\bigg)
- \frac{1}{N}\sum\limits_{i=1}^N \ell\bigg(\sum\limits_{m\in S} (h^m_i)^{t} + \sum\limits_{m\notin S} (h^m_i)^{t-1}; y_i\bigg)
Problem: In round t, the server only has
\{ (h_i^m)^t \mid i \in B^t \}
Embedding matrix
\mathcal{H}^m \in \mathbb{R}^{T \times N} \enspace\text{with}\enspace \mathcal{H}^m_{t, i} = (h_i^m)^t
Theorem
If the loss function is smooth, then
\mathop{rank}_\epsilon(\mathcal{H}^m) \in \mathcal{O}(\frac{\log(T)}{\epsilon})
[Fan et al.'22]
Contribution Valuation
By Zhenan Fan
Contribution Valuation
Slides for my PhD defence.
- 246



