МЕХАНИКА

"Большая перемена"

ОГЭ

1. Танк едет со скоростью v = 60 км/ч. С какой скоростью движутся верхние траки гусениц танка?

120 км/ч

Разминка

2. Доска длиной L одним концом лежит на цилиндре. Другой конец удерживается человеком, который толкает ее вперед, вследствие чего цилиндр катится без проскальзывания (см. рисунок). Какой путь пройдет человек, дойдя до цилиндра?

S = 2L

3. Определите скорость тела u, считая скорость v известной (см. рисунок). Нити нерастяжимы, рычаги жесткие.

a) вверх v/2

Разминка

б) вниз 2v/3

в) вниз 7v/12

г) вверх 14v/3

Нестандартные методики

Векторное произведение

Опр.:

1) \, |\vec{c}| = |\vec{a}|\cdot|\vec{b}|\cdot \sin(\alpha)
\alpha

где

,
2) \, \vec{c} \perp \vec{a};
\vec{c} \perp \vec{b};
3)

- угол между векторами      и    

\vec{a}
\vec{b};

Векторное произведение двух векторов      и      - это такой вектор     , который удовлетворяет следующим требованиям:

\vec{a}
\vec{b}
\vec{c}

Векторы           и     - образуют правую тройку.

\vec{a}
\vec{b}
\vec{c}
,
\vec{c} = \vec{a}\times\vec{b} = [\vec{a}, \vec{b}]

Обз.:

Правая тройка векторов

Опр.:

\vec{a}
\vec{c}
\vec{b}
\vec{a}
\vec{c}
\vec{b}
\vec{a}
\vec{c}
\vec{b}
\vec{a}
\vec{c}
\vec{b}
\vec{c} = \vec{a}\times\vec{b}
\vec{c} = \vec{b}\times\vec{a}
\vec{b} = \vec{c}\times\vec{a}
\vec{b} = \vec{a}\times\vec{c}

Тройка векторов           и      - называется правой, если кратчайший

поворот от вектора       до вектора     виден из конца вектора     против часовой стрелки.

\vec{a},
\vec{b}
\vec{c}
\vec{a}
\vec{b}
\vec{c}

Момент сил

Опр.:

\vec{M}
=
\vec{r}
\times
\vec{F}

Радиус вектор из точки отсчета до точки приложения силы

Момент силы F относительно точки отсчета

\vec{r}
\vec{F}
\vec{M}

Точка отсчета

Точка приложения силы

Момент сил

|\vec{M}|
=
|\vec{r}|
\cdot
|\vec{F}|

Плечо сил

\cdot
\sin(\alpha)
|\vec{r}|
\cdot
\sin(\alpha)
=
l

Кратчайшее расстояние до линии действия силы

=
M
=
F\cdot l

Выбор знака определяется через векторное произведение

\vec{r}
\vec{F}
\alpha
180^{\circ}-\alpha
l
\sin(180^{\circ} - \alpha)
=
\sin(\alpha)
\cdot r

Плоская система сил

\vec{r}
\vec{F}
\vec{M}
y
x
\odot
=
"+"
\vec{r}
\vec{F}
\vec{M}
y
x
=
"-"
\otimes
  • Если все силы действуют в одной плоскости, то моменты всех сил будут этой плоскости перпендикулярны.
  • Если сила вращает тело относительно точки отсчета против часовой стрелки, то момент силы направлен "к нам" и знак будет положительным ("+"). В противном случае знак будет отрицательным ("-").

Плоскопараллельное движение

Опр.:

Плоскопараллельное движение - вид движения абсолютно твёрдого тела, при котором траектории всех точек тела располагаются в плоскостях, параллельных заданной плоскости.

Мгновенный центр скоростей (МЦС)

Опр.:

Мгновенный центр скоростей — при плоскопараллельном движении абсолютно твёрдого тела точка, связанная с этим телом, которая обладает следующими свойствами: 

а) её скорость в данный момент времени равна нулю; 

б) относительно неё в данный момент времени вращается тело. Она существует в любой момент времени, но её положение меняется со временем.

Движение колеса без проскальзывания

\vec{v}_с
\vec{v}_с
\vec{v}_{T относит. C}

Некоторая точка колеса

Точка колеса, скорость которой равна нулю

Мгновенный центр скоростей МЦС

T
\vec{v}_{рез}

=

Положение МЦС

Алгоритм:

  • Определяем направления скоростей любых двух различных точек тела, скорости которых НЕ параллельны;
  • Проводим перпендикуляры к прямым, параллельным линейным скоростям выбранных точек тела;
  • В точке пересечения этих перпендикуляров и будет находиться мгновенный центр скоростей.
\vec{v}_с
\vec{v}_A
A
\vec{v}_B
B
B
A
\vec{v}_A
\vec{v}_B
B
A
\vec{v}_A
\vec{v}_B
\vec{v}_A = \vec{v}_{рез. A}
\vec{v}_с
\vec{v}_с

Положение МЦС

  • Если векторы линейных скоростей двух различных точек тела параллельны друг другу, и отрезок, соединяющий эти точки, не перпендикулярен векторам этих скоростей, то перпендикуляры к этим векторам также параллельны. В этом случае говорят, что мгновенный центр скоростей находится в бесконечности, и тело движется мгновенно поступательно.
\vec{v}_с
\vec{v}_A
A
\vec{v}_B
B
\vec{v}_A
\vec{v}_B
\vec{v}_с
=
=

Положение МЦС

  • Если известны скорости двух точек, и эти скорости параллельны друг другу, и кроме того, указанные точки лежат на прямой, перпендикулярной скоростям, то положение мгновенного центра скоростей определяется так, как показано на рисунках
\vec{v}_A
A
\vec{v}_B
B
\vec{v}_A
A
\vec{v}_B
B

Удобство использования МЦС

  • В случае вращательного движения все точки твердого тела вращаются с одинаковыми угловыми скоростями. Определив мгновенный центр скоростей, можно определить линейную скорость любой точки тела.
B
A
\vec{v}_A
\vec{v}_B
\omega
\omega
R_A
R_B
v_A
=
R_A
\omega
v_B
=
R_B
\omega

Пример 1

\vec{v}_A
\vec{v}_B

МЦС

Пример 2

\vec{v}_с
\vec{v}_B
A
O
B
v_A
v_с
=
\omega
R
R
=
\omega
2R
=
2v_с
v_B
=
\omega
R\sqrt{2}

Пример 3

Катушку тянут за нить. Радиус катушки R1 = 10 см, радиус барабана R2 = 5 см, скорость относительно земли v = 15 м/с. Определите скорость центра катушки и точки А, относительно земли.

\vec{v}_с
R_1
O
C
R_2
B
A
\vec{v}

МЦС

v_B
=
v
=
\omega (R_1 + R_2)
\omega
=
\dfrac{v}{R_1 + R_2}
v_C
=
\omega R_1
v_A
=
\omega 2R_1

Пример 4

Определите скорость груза Е, исходя из рисунка

\vec{v}
A
B
C
D
E
A_1
A_2

МЦС

МЦС

v_{A_2}
=
v
O_A
v_{O_A}
=
\dfrac{v_{A_2}}{2}
v_{B_2}
=
v_{O_A}
...
v_{E}
=
\dfrac{v}{16}

ЕГЭ

Кодификатор

1.3 Статика
1.3.1 Момент силы относительно оси вращения:
                     
                      где          плечо силы

относительно оси, проходящей через точку О перпендикулярно рисунку
1.3.2 Условия равноевися тела в ИСО:




 
M = Fl,
l -
\vec{F}
\begin{cases} M_1 + M_2 + ... = 0 \\ \vec{F}_1 + \vec{F}_2 + ... = 0 \end{cases}

Задача 1

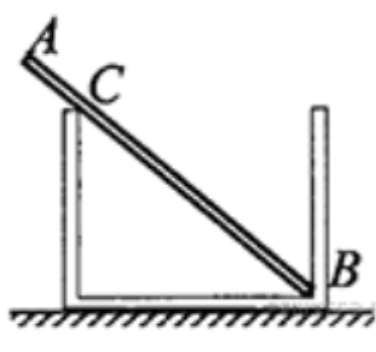
Однородный стержень AB массой m = 100 г покоится, упираясь в стык дна и стенки банки концом B и опираясь на край банки в точке C (см. рисунок). Модуль силы, с которой стержень давит на стенку сосуда в точке C, равен 0.5 Н. Чему равен модуль вертикальной составляющей силы, с которой стержень давит на сосуд в точке B, если модуль горизонтальной составляющей этой силы равен 0.3 Н? Трением пренебречь. Ответ укажите в ньютонах с точностью до одного знака после запятой.

Задача 2

На гладкой горизнтальной плоскости лежит два груза массами m1 = 0.5 кг и m2 = 2 кг, соединенные невесомой нерастяжимой нитью, перекинутой через два неподвижных (А и В) и один подвижный (О) невесомые блоки, как показано на рисунке. Оси блоков горизонтальны, трения в осях блоков нет. К оси О подвижного блока приложена направленная вертикально вниз сила F = 4 Н. Найдите ускорение этой оси. Сделайте схематический рисунок с указанием сил, действующих на грузы и блок.

Задача 3

К двум вертикально расположенным пружинам одинаковой длины подвесили однородный стержень длиной L = 30 см. Если к этому стержню подвесить груз массой m = 3 кг на расстоянии d = 5 см от правой пружины, то стержень будет расположен горизонтально, и растяжения обеих пружин будут одинаковы (см. рисунок). Жесткость левой пружины в 2 раза меньше, чем правой. Чему равна масса стержня M? Сделайте рисунок с указанием используемых в решении сил.

Задача 4

В системе, изображённой на рисунке, масса груза, лежащего на шероховатой горизонтальной плоскости, равна m = 2 кг. При подвешивании к оси подвижного блока груза массой M = 2,5 кг он движется вниз с ускорением a = 2 м/с2. Чему равен коэффициент трения μ между грузом массой m и плоскостью? Нити невесомы и нерастяжимы, блоки невесомы, трение в осях блоков и о воздух отсутствует.

Задача 5

Очень лёгкая рейка уравновешена в горизонтальном положении. Правым концом она прикреплена к шарниру O. К левому концу рейки прикреплена невесомая нерастяжимая нить, которая натягивается с помощью невесомого подвижного блока, к оси которого подвешен груз массой 20 г. К средней части рейки прикреплён воздушный шарик, наполненный лёгким газом. Определите объём этого шарика, пренебрегая массой его оболочки и массой газа, находящегося в шарике. Плотность атмосферного воздуха 1,2 кг/м3. Ответ приведите в литрах.

Задача 6

В системе, изображённой на рисунке, грузик массой m = 1 кг подвешен на нити, охватывающей три блока, второй конец которой привязан к оси самого правого блока (см. рис.). К этой же оси привязана другая нить, соединяющаяся с грузом массой M = 11 кг, лежащим на шероховатой горизонтальной плоскости (коэффициент трения груза о плоскость равен μ = 0,25). Найдите ускорение a1 грузика m. Считайте, что нити невесомы и нерастяжимы, свободные участки нитей вертикальны или горизонтальны, блоки невесомы, а трение в их осях отсутствует.

Задача 7

Невесомый стержень длиной 3 м расположен в стакане по углом 45о (см. рисунок). На расстоянии 1м от угла подвешен шарик массой 3 кг. Найдите силу, с которой стержень давит на стенку стакана.

Задача 8

Найдите модуль ускорения A груза массой М в системе, изображённой на рисунке. Трения нет, блоки невесомы, нити лёгкие и нерастяжимые, их участки, не лежащие на блоках, вертикальны, масса второго груза m, ускорение свободного падения равно g.

Задача 9

В системе, изображённой на рисунке, трения нет, блоки невесомы, нить невесома и нерастяжима, m1 = 2 кг, m2 = 4 кг, m3 = 1 кг. Найдите модуль и направление ускорения a3 груза массой m3.

Задача 10

На горизонтальном шероховатом столе лежит брусок массой m1 = 2 кг, соединённый через систему идеальных блоков невесомой и нерастяжимой нитью с грузом массой m2 = 3 кг, висящим на высоте h = 2 м над столом (см. рисунок). Груз начинает движение без начальной скорости и абсолютно неупруго ударяется о стол. Какое количество теплоты Q выделяется при этом ударе? Коэффициент трения бруска о стол равен μ = 0,25.

Спасибо за понимание!

Механика

By Alexey Baigashov

Made with Slides.com

Механика

  • 538

More from Alexey Baigashov