Занятие №20:
Решение задач
Задача №1
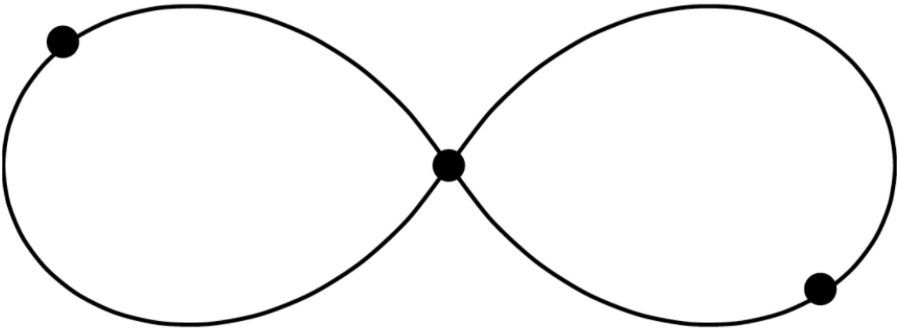
Астрономы открыли необычную тройную звездную систему, состоящую из трех одинаковых звезд, движущихся друг за другом по орбите, изображенной на рисунке. Чему равно максимально возможное изменение видимой звездной величины этой системы для внешнего наблюдателя?
Решение
Дано:
m
m
Найти:
Решение:
какая-то дичь ...
какую-то дичь ...
m
m
m
m
m
m
m
m
m
m
m
m
mобщ
m_{\text{общ}}
Решение
mобщ
m_{\text{общ}}
=
=
−2.5
-2.5
⋅
\cdot
log10(3⋅2.512−m)
\log_{10}(3\cdot2.512^{-m})
mсис
m_{\text{сис}}
∈
\in
[m,mобщ]
[m, m_{\text{общ}}]
Задача №2
Можно ли поверить мужику, утверждающему, что он видел Венеру, сияющую так же ярко как все звезды ночного неба вместе взятые?
Принять, что распределение звезд на небе соответствует следующим значениям:
[0m,1m]−14штук
[0^m, 1^m] - 14 \, \text{штук}
[1m,2m]−3⋅14штук
[1^m, 2^m] - 3\cdot14 \, \text{штук}
[2m,3m]−3⋅3⋅14штук
[2^m, 3^m] - 3\cdot3\cdot14 \, \text{штук}
....
....
Решение
Дано:
Найти:
Решение:
куча звезд
веру в мужика
mобщ
m_{\text{общ}}
=
=
−2.5
-2.5
⋅
\cdot
log10(2.512−0.5⋅14+2.512−1.5⋅14⋅3++2.512−2.5⋅14⋅3⋅3+...+2.512−5.5⋅14⋅3⋅3⋅3⋅3⋅3)
\log_{10}(2.512^{-0.5}\cdot14 + 2.512^{-1.5}\cdot14\cdot3 + \\
+ 2.512^{-2.5}\cdot14\cdot3\cdot3 + ... \\
+ 2.512^{-5.5}\cdot14\cdot3\cdot3\cdot3\cdot3\cdot3)
≈
\approx
≈
\approx
−4.6m
-4.6^m
Задача №3
Суммарная звездная величина двух звезд 5m. Блеск одной из звезд 5,5m. Определите звездную величину второй звезды.
Решение
Дано:
Найти:
Решение:
mобщ
m_{\text{общ}}
=
=
−2.5
-2.5
⋅
\cdot
mобщ=5;
m_{\text{общ}}=5;
m1=5.5
m_1=5.5
m2−?
m_2-?
log10(2.512−m1+2.512−m2)
\log_{10}(2.512^{-m_1} + 2.512^{-m_2})
=5.5
=5.5
=5
=5
5
5
=
=
−2.5
-2.5
⋅
\cdot
log10(2.512−5.5+2.512−m2)
\log_{10}(2.512^{-5.5} + 2.512^{-m_2})
∣:−2.5
|:-2.5
−2
-2
=
=
log10(2.512−5.5+2.512−m2)
\log_{10}(2.512^{-5.5} + 2.512^{-m_2})
Решение
10−2
10^{-2}
=
=
2.512−5.5+2.512−m2
2.512^{-5.5} + 2.512^{-m_2}
=0.01
=0.01
≈0.006
\approx0.006
0.01−0.006
0.01 - 0.006
=
=
2.512−m2
2.512^{-m_2}
0.0036
0.0036
=
=
2.512−m2
2.512^{-m_2}
m2
m_2
=
=
−log10(2.512)log10(0.0036)
-\dfrac{\log_{10}(0.0036)}{\log_{10}(2.512)}
≈
\approx
6m
6^m
Спасибо за понимание!
Занятие №20: Решение задач
Занятие 20. Решение задач
By Alexey Baigashov
Занятие 20. Решение задач
- 278
