Causal Dynamical Triangulations with CGAL
Adam Getchell
acgetchell@ucdavis.edu
University of California, Davis
CGAL Developers Conference, Nancy, Sept 29-October 2, 2015
Causal Dynamical Triangulations
A candidate theory of quantum gravity
CGAL
You are the experts!
Path Integral
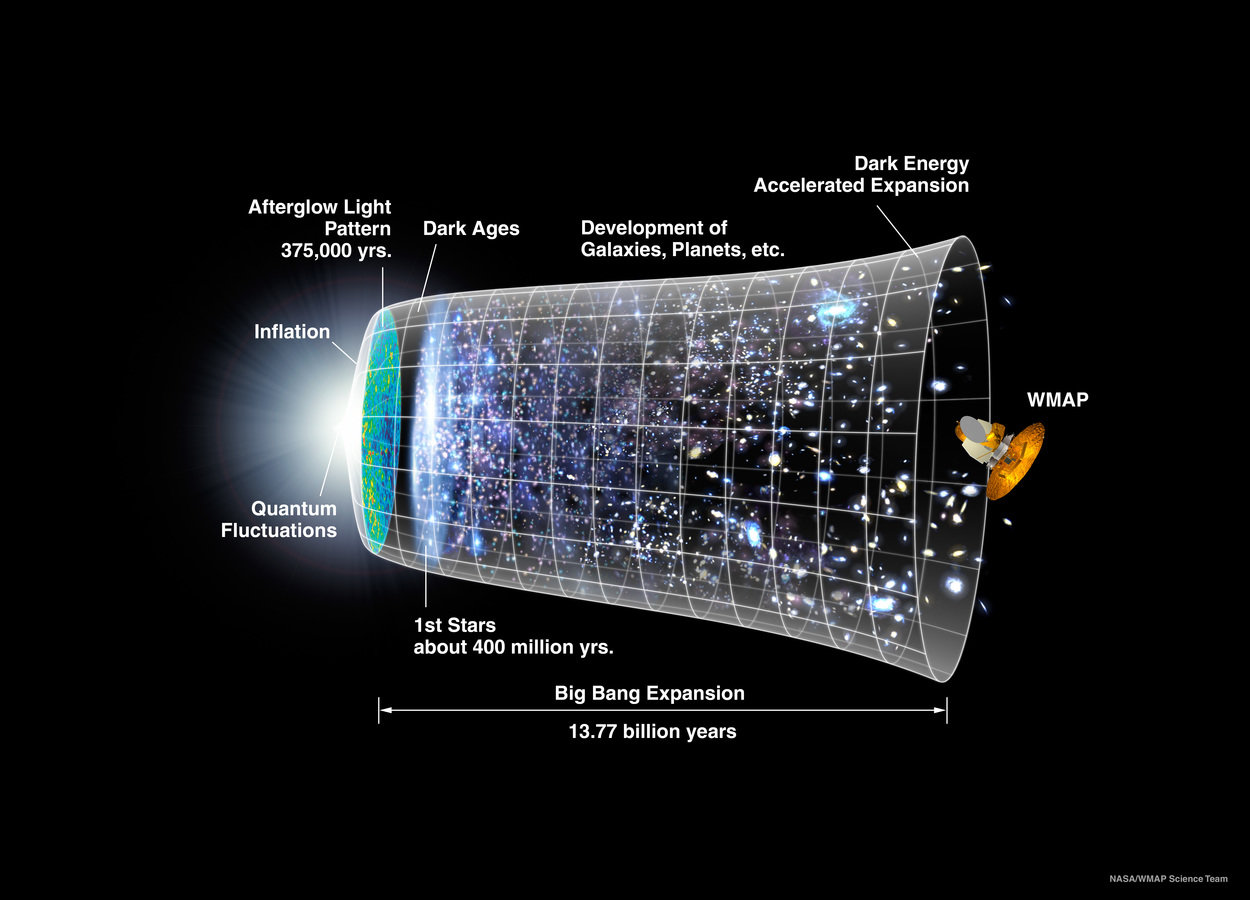
Credit: NASA/WMAP Science team
Path Integral
\langle B|T|A\rangle=\int\mathcal{D}[g]e^{iS_{EH}}
⟨B∣T∣A⟩=∫D[g]eiSEH
S_{EH}=\frac{1}{16\pi G_{N}}\int d^{4}x\sqrt{-g}(R-2\Lambda)
SEH=16πGN1∫d4x−g(R−2Λ)
Equations of Motion
\partial S = 0 \rightarrow R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}=8\pi G_{N}T_{\mu\nu}
∂S=0→Rμν−21Rgμν=8πGNTμν
Ricci scalar
Cosmological constant
Ricci tensor
Ricci scalar
Stress-Energy tensor
Transition probability amplitude
Calculating the Path Integral
\langle B|T|A\rangle=\int\mathcal{D}[g]e^{iS_{EH}}
⟨B∣T∣A⟩=∫D[g]eiSEH
S_{EH}=\frac{1}{16\pi G_{N}}\int d^{4}x\sqrt{-g}(R-2\Lambda)
SEH=16πGN1∫d4x−g(R−2Λ)
Almost impossible to calculate!
Calculating the Path Integral
Quickly gets complicated!
Perturbative sums, renormalization, etc.
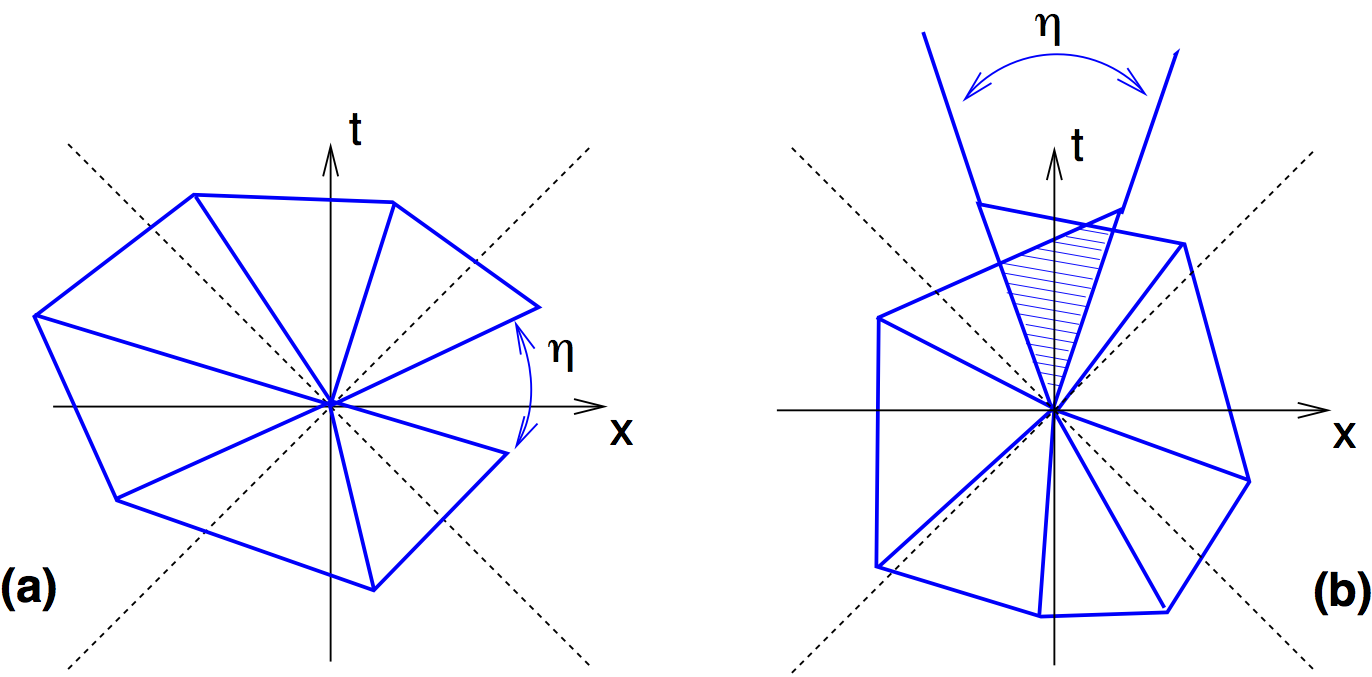
CDT Path Integral
3D Delaunay Triangulation: 256 Timeslices, 7473 Vertices, 47021 Simplices
2D Icosahedron: 1 timeslice, 30 vertices, 20 Simplices
CDT Path Integral
\langle B|T|A\rangle=\sum\limits_{triangulations}\frac{1}{C(T)}e^{iS_{R}(T)}
⟨B∣T∣A⟩=triangulations∑C(T)1eiSR(T)
S_{R}=\frac{1}{8\pi G_{N}}\left(\sum\limits_{hinges}A_{h}\delta_{h}-\Lambda\sum\limits_{simplices}V_{s}\right)
SR=8πGN1(hinges∑Ahδh−Λsimplices∑Vs)
Inequivalent Triangulations
Regge Action
Partition Function
Transition probability amplitude
Calculating the CDT Path Integral
S_{R}=\frac{1}{8\pi G_{N}}\left(\sum\limits_{hinges}A_{h}\delta_{h}-\Lambda\sum\limits_{simplices}V_{s}\right)
SR=8πGN1(hinges∑Ahδh−Λsimplices∑Vs)
Area of hinge
Volume of Simplex
Deficit Angle
Regge Action
CDT Action
\begin{array}{l}
S^{(3)} &=& 2\pi k\sqrt{\alpha}N_1^{TL} \\
&+& N_3^{(3,1)}\left[-3k\text{arcsinh}\left(\frac{1}{\sqrt{3}
\sqrt{4\alpha +1}}\right)-3k\sqrt{\alpha}\text{arccos}\left(\frac{2\alpha+1}
{4\alpha+1}\right)-\frac{\lambda}{12}\sqrt{3\alpha+1}\right] \\
&+& N_3^{(2,2)}\left[2k\text{arcsinh}\left(\frac{2\sqrt{2}\sqrt{2\alpha+1}}
{4\alpha +1}\right)-4k\sqrt{\alpha}\text{arccos}\left(\frac{-1}{4\alpha+1}
\right)-\frac{\lambda}{12}\sqrt{4\alpha +2}\right]
\end{array}
S(3)=++2πkαN1TLN3(3,1)[−3karcsinh(34α+11)−3kαarccos(4α+12α+1)−12λ3α+1]N3(2,2)[2karcsinh(4α+1222α+1)−4kαarccos(4α+1−1)−12λ4α+2]
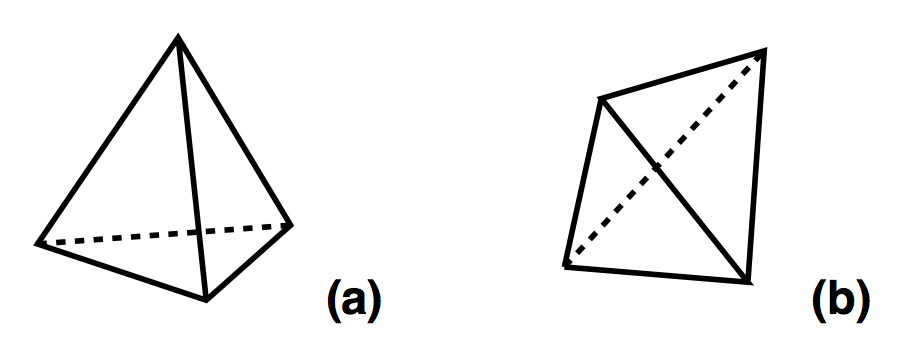
3D
CDT Action
4D
\begin{array}{l}
S^{(4)}\!\! &=&\!\! \frac{k \pi}{2} \sqrt{4\alpha +1}\ N_{2}^{TL}
+ N_{4}^{(4,1)}\cdot \\
&&
\!\!\Biggl( -\sqrt{3} k\ {arcsinh} \frac{1}{2\sqrt{2}\sqrt{3\alpha +1}}
-\frac{3 k}{2} \sqrt{4\alpha +1} \arccos\frac{2\alpha +1}{2 (3\alpha +1)}
-\lambda \frac{\sqrt{8\alpha +3}}{96}
\Biggr) \\
&+&\!\! N_{4}^{(3,2)}
\Biggl( \frac{\sqrt{3} k}{4}\ {arcsinh}\frac{\sqrt{3}\sqrt{12 \alpha +7}}
{2 (3 \alpha+1)}
- \frac{3 k}{4} \sqrt{4\alpha +1}\\
&&\!\!\biggl( 2\arccos\frac{-1}{2\sqrt{2}\sqrt{2\alpha +1}\sqrt{3\alpha +1}} +
\arccos\frac{4\alpha +3}{4 (2\alpha +1)}\biggr)
-\lambda \frac{\sqrt{12\alpha +7}}{96}\Biggr)
\end{array}
S(4)=+2kπ4α+1 N2TL+N4(4,1)⋅(−3k arcsinh223α+11−23k4α+1arccos2(3α+1)2α+1−λ968α+3)N4(3,2)(43k arcsinh2(3α+1)312α+7−43k4α+1(2arccos222α+13α+1−1+arccos4(2α+1)4α+3)−λ9612α+7)
CDT Path Integral
\langle B|T|A\rangle=\sum\limits_{triangulations}\frac{1}{C(T)}e^{iS_{R}(T)}
⟨B∣T∣A⟩=triangulations∑C(T)1eiSR(T)
CDT Path Integral
\langle B|T|A\rangle=\sum\limits_{triangulations}\frac{1}{C(T)}e^{-S_{R}(T)}
⟨B∣T∣A⟩=triangulations∑C(T)1e−SR(T)
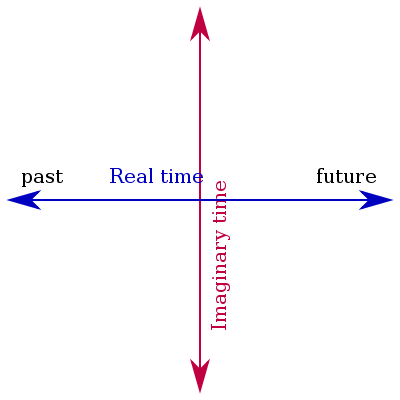
Wick rotation
Metropolis-Hastings
\langle B|T|A\rangle=\sum\limits_{triangulations}\frac{1}{C(T)}e^{-S_{R}(T)}
⟨B∣T∣A⟩=triangulations∑C(T)1e−SR(T)
Inequivalent Triangulations
Partition Function
Wick rotation
- Pick an ergodic (Pachner) move
- Make that move with a probability of a1a2, where:
a_{1}=\frac{move[i]}{\sum\limits_{i}move[i]}
a1=i∑move[i]move[i]
a_{2}=e^{\Delta S}
a2=eΔS
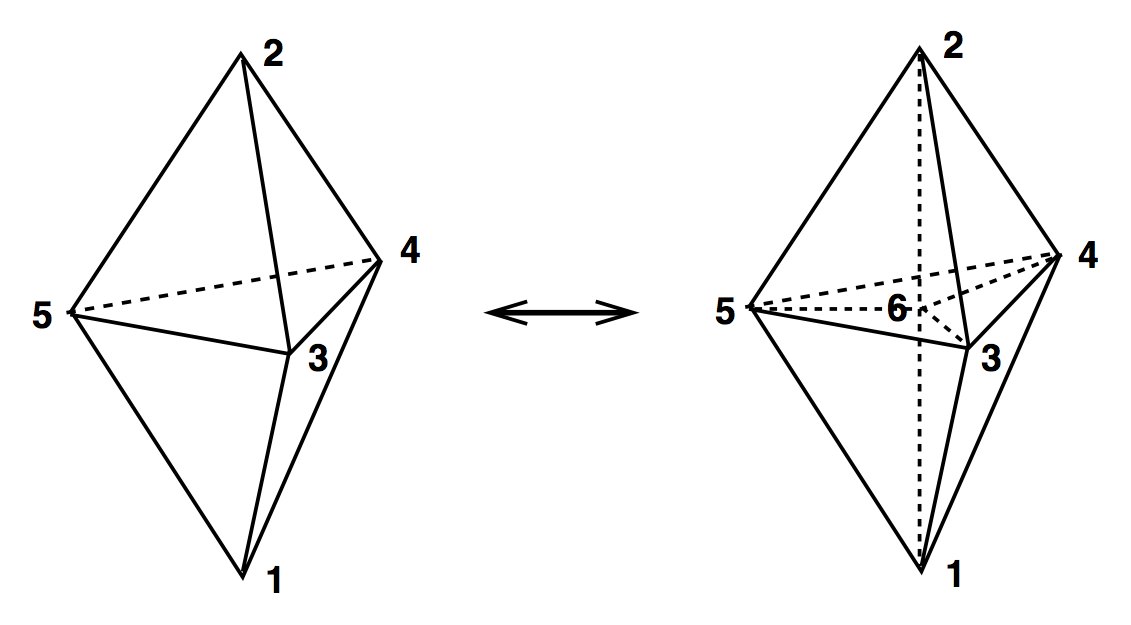
3D Ergodic Moves
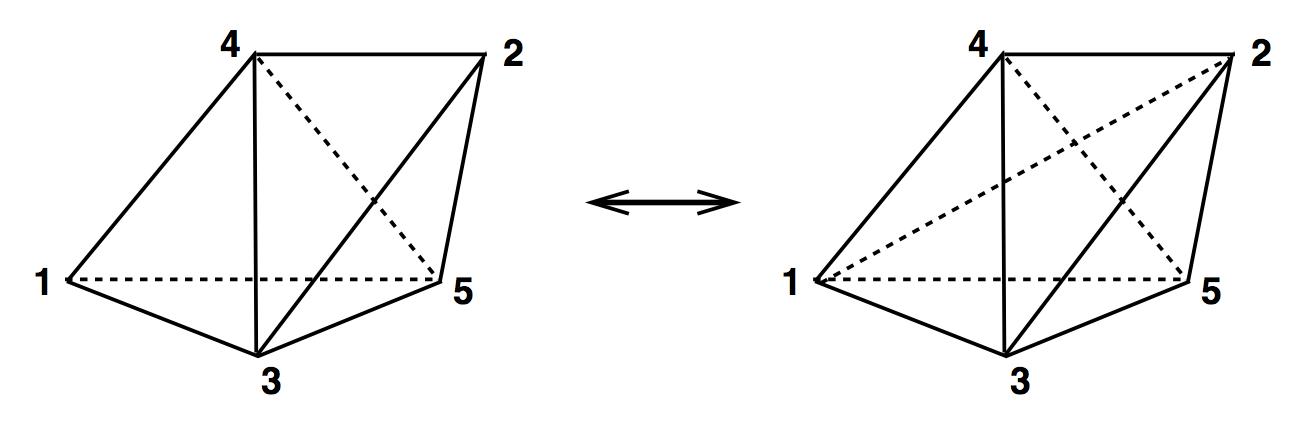
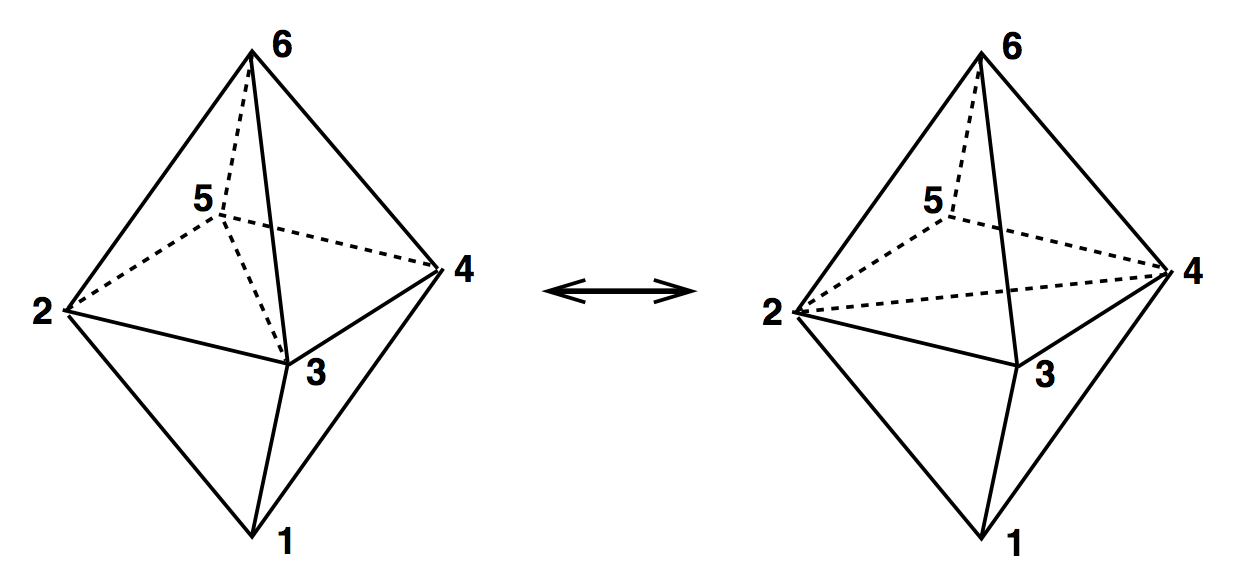
(2,3) & (3,2)
(4,4)
(2,6) & (6,2)
Simplices involved
Move name
(3,1) & (2,2)
2 (1,3) & 2 (3,1)
(1,3) & (3,1)
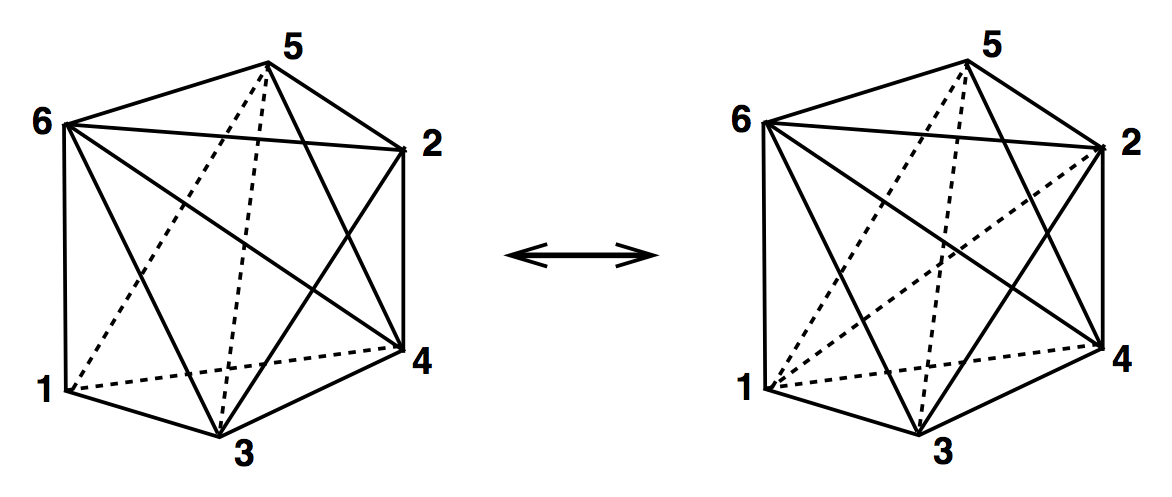
4D Ergodic Moves
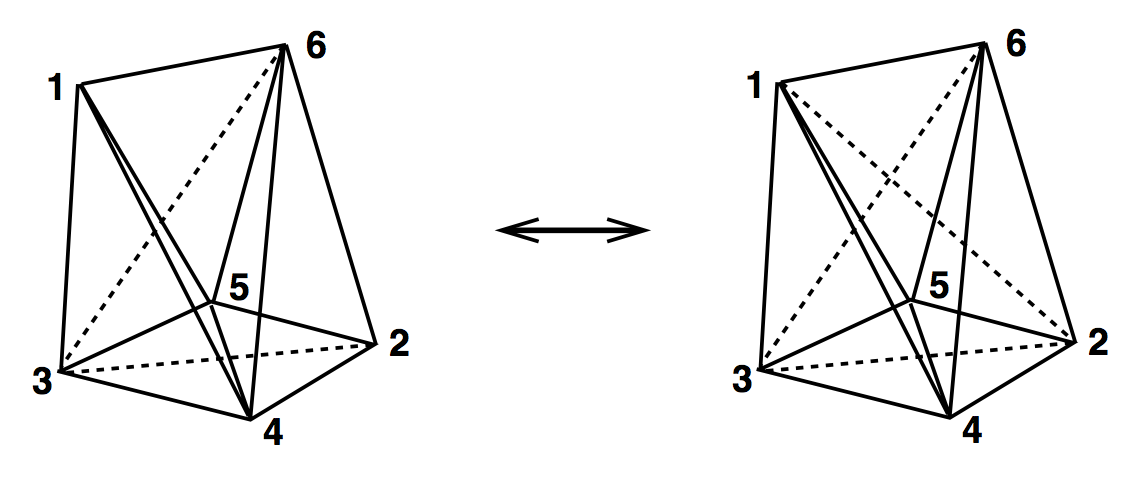
(2,4) & (4,2)
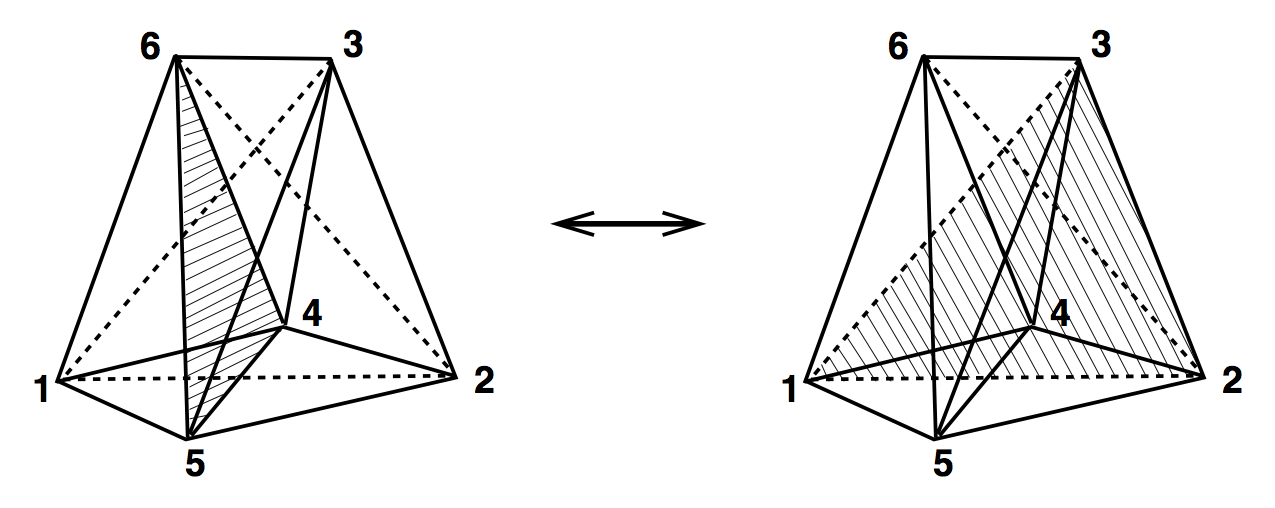
(3,3)
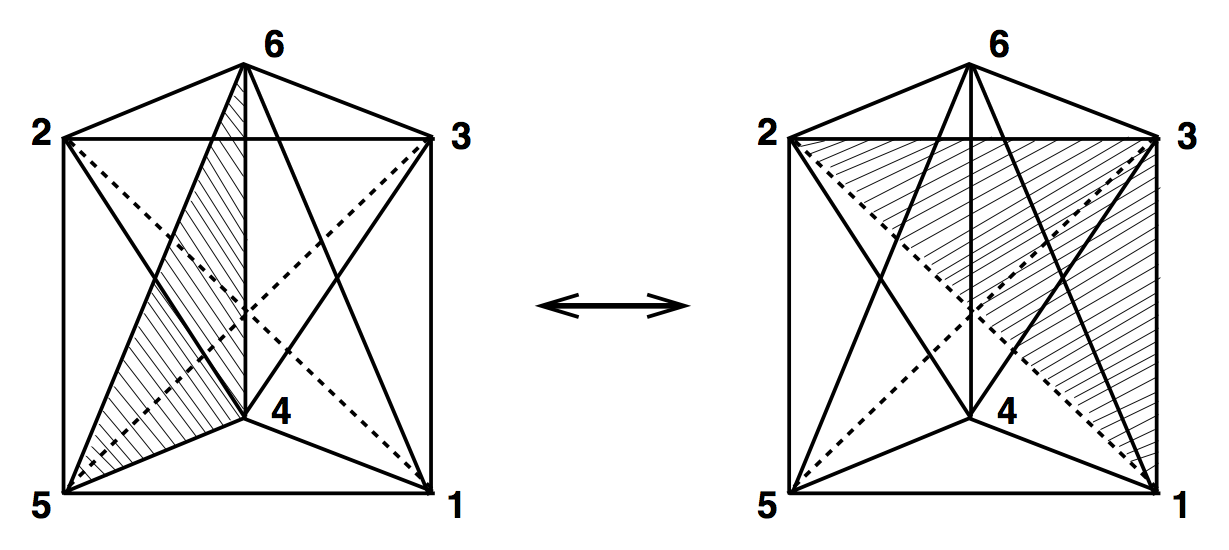
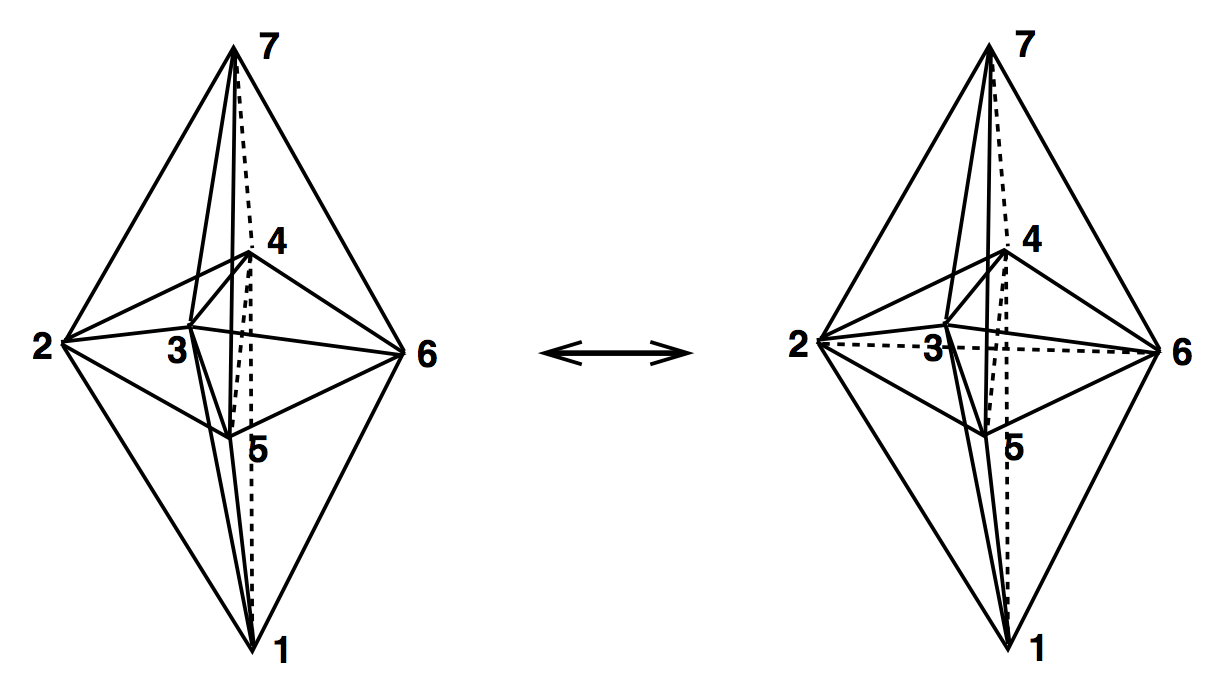
(4,6) & (6,4)
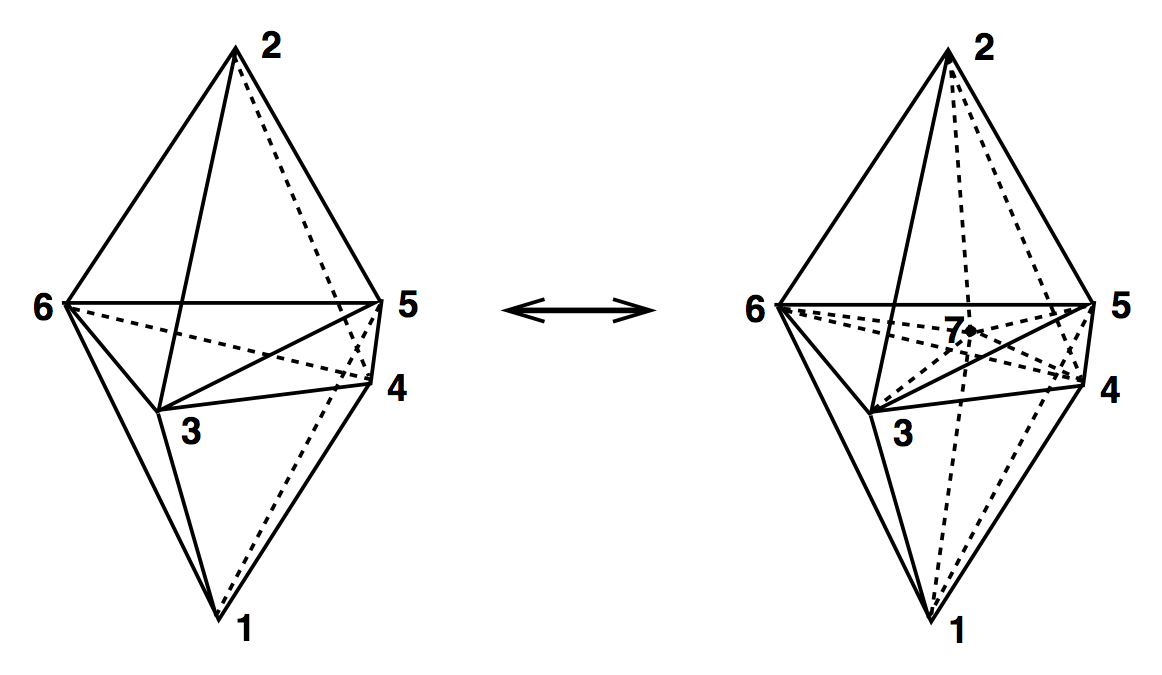
(2,8) & (8,2)
Does CDT have a Newtonian Limit?
CDT looks like GR at cosmological scales, does it have a Newtonian limit?
F=G_{N}\frac{m_{1}m_{2}}{r^2}
F=GNr2m1m2
At first glance, this is hard:
- CDT is not well-suited for approximating smooth classical space-times
- We don't have the time or resolution to watch objects fall
A Trick from GR
ds^{2} = e^{2\lambda}dt^{2} - e^{2\left(\nu-\lambda\right)}\left(dr^{2}+dz^{2}\right)
- r^{2}e^{-2\lambda}d\phi^{2}
ds2=e2λdt2−e2(ν−λ)(dr2+dz2)−r2e−2λdϕ2
The static axisymmetric Weyl metric:
With two-body Chazy-Curzon (circa 1924) solutions of the Einstein field equations:
\lambda(r,z)=-\frac{\mu_1}{r_1}-\frac{\mu_2}{r_2}
λ(r,z)=−r1μ1−r2μ2
\nu(r,z)=\frac{1}{2}\frac{\mu_{1}^{2}r^2}{r_{1}^{4}}-\frac{1}{2}\frac{\mu_{2}^{2}r^2}{r_{2}^{4}}+\frac{2\mu_1\mu_2}{(z-z_2)^2}\left[\frac{r^2+(z-z_1)(z-z_2)}{r_{1}r_{2}}-1\right]
ν(r,z)=21r14μ12r2−21r24μ22r2+(z−z2)22μ1μ2[r1r2r2+(z−z1)(z−z2)−1]
r_1=\sqrt{r^2+(z-z_1)^2}
r1=r2+(z−z1)2
Leads to a strut:
With a stress:
That can be integrated to get the Newtonian force!
\nu(0,z)=\frac{4\mu_{1}\mu_{2}}{z_{1}^2-z_{2}^2}
ν(0,z)=z12−z224μ1μ2
T_{zz}=\frac{1}{8\pi G_{N}}\left(1-e^{-\nu(r,z)}\right)2\pi\delta
Tzz=8πGN1(1−e−ν(r,z))2πδ
F=\int T_{zz}dA=\frac{1}{4G_{N}}\left(1-e^{-\nu(r,z)}\right)=G_{N}\frac{m_1m_2}{z_1^2-z_2^2}\:\text{for}\:\mu_i=G_Nm_i
F=∫TzzdA=4GN1(1−e−ν(r,z))=GNz12−z22m1m2forμi=GNmi
A Trick from GR
ds^{2} = e^{2\lambda}dt^{2} - e^{2\left(\nu-\lambda\right)}\left(dr^{2}+dz^{2}\right)
- r^{2}e^{-2\lambda}d\phi^{2}
ds2=e2λdt2−e2(ν−λ)(dr2+dz2)−r2e−2λdϕ2
g_{\mu\nu}=\left(\begin{array}{cccc}
e^{2\lambda} & 0 & 0 & 0\\
0 & -e^{2\left(\nu-\lambda\right)} & 0 & 0\\
0 & 0 & -e^{2\left(\nu-\lambda\right)} & 0\\
0 & 0 & 0 & -\frac{r^{2}}{e^{2\lambda}}
\end{array}\right)
gμν=e2λ0000−e2(ν−λ)0000−e2(ν−λ)0000−e2λr2
\Gamma_{\mu\nu}^{\lambda}=\frac{1}{2}g^{\lambda\sigma}\left(\partial_{\mu}g_{\nu\sigma}+\partial_{\nu}g_{\sigma\mu}-\partial_{\sigma}g_{\mu\nu}\right)
Γμνλ=21gλσ(∂μgνσ+∂νgσμ−∂σgμν)
R_{\sigma\mu\nu}^{\rho}=\partial_{\mu}\Gamma_{\nu\sigma}^{\rho}-\partial_{\nu}\Gamma_{\mu\sigma}^{\rho}+\Gamma_{\mu\lambda}^{\rho}\Gamma_{\nu\sigma}^{\lambda}-\Gamma_{\nu\lambda}^{\rho}\Gamma_{\mu\sigma}^{\lambda}
Rσμνρ=∂μΓνσρ−∂νΓμσρ+ΓμλρΓνσλ−ΓνλρΓμσλ
R_{\mu\nu}=R^{\rho}_{\mu\rho\nu}
Rμν=Rμρνρ
R=R^{\mu}_{\mu}
R=Rμμ
R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}=8\pi G_{N}T_{\mu\nu}
Rμν−21Rgμν=8πGNTμν
Metric
Affine connection
Riemann tensor
Ricci tensor & Ricci scalar
Einstein field equations
My Work
Find the Newtonian Limit, if it exists
- Test case, no limit in 3D
Re-implement CDT
- Rewrite in modern C++
- Use well-known libraries
My Work
Use current tools
- LLVM/Clang
- Hosted on GitHub
- Continuous integration with Travis-CI
- Google Style Guide
- GoogleTest/GoogleMock
- CMake for cross-platform building
- Literate programming with Doxygen
- Others (Gitter, Ninja, etc.)
Easy to evaluate, use, and contribute
My Work
Mass = Epp quasilocal energy
E_E\equiv\frac{1}{8\pi G_N}\int_{\Omega}d^2x\sqrt{|\sigma|}\left(\sqrt{k^2-l^2}-\sqrt{\bar{k}^2-\bar{l}^2}\right)
EE≡8πGN1∫Ωd2x∣σ∣(k2−l2−kˉ2−lˉ2)
l\equiv\sigma^{\mu\nu}l_{\mu\nu}
l≡σμνlμν
k\equiv\sigma^{\mu\nu}k_{\mu\nu}
k≡σμνkμν
- In 1+1 simplicial geometry, extrinsic curvature at a vertex is proportional to the number of connected triangles
- In 2+1 simplicial geometry, extrinsic curvature at an edge is proportional to the number of connected tetrahedra
- In 3+1 simplicial geometry, extrinsic curvature at a face is proportional to the number of connected pentachorons (4-simplices)
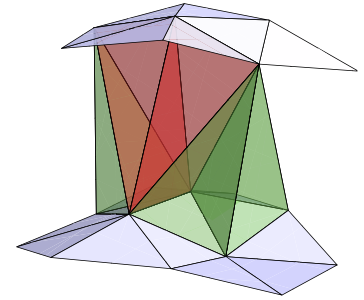
My Work
Non-Euclidean Distance
- Calculate single-source shortest path between the two masses using Bellman-Ford algorithm in O(VE)
- Modify allowed moves to not permit too many successive moves which increase or decrease distance between masses (hold relatively fixed)
Hausdorff Distance(?)
- Calculate Voronoi diagram of Delaunay triangulation
- Find minimal Hausdorff distance in diagram for sets in O((m+n)^6 log(mn)) (Huttenlocher, Kedem, and Kleinberg)
Fast foliated Delaunay Triangulations in CGAL
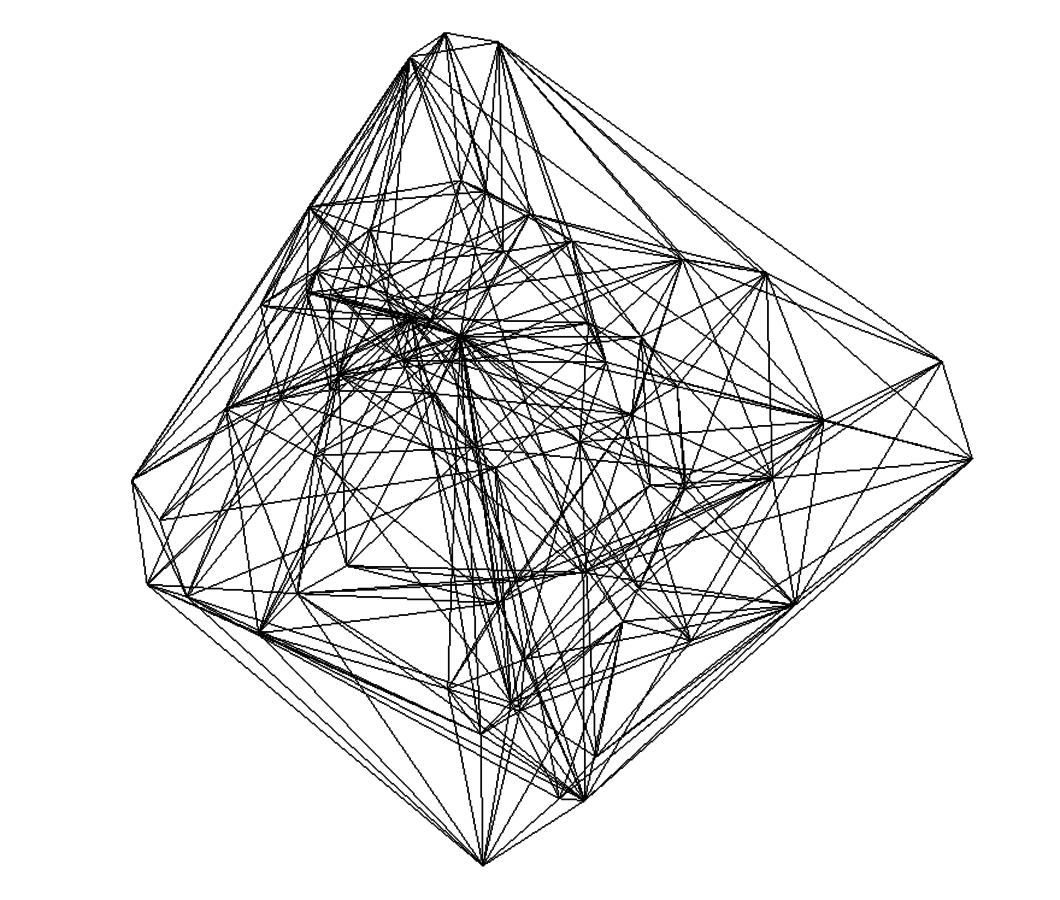
8 timeslices, 68 vertices, 619 faces, 298 simplices
Creation time: 0.043336s
(MacBook Pro Retina, Mid 2012)
Fast foliated Delaunay Triangulations in CGAL
/// @param[in] simplices The number of desired simplices in the triangulation
/// @param[in] timeslices The number of timeslices in the triangulation
/// @returns A std::unique_ptr to the foliated Delaunay triangulation
auto inline make_triangulation(const unsigned simplices,
const unsigned timeslices) {
std::cout << "Generating universe ... " << std::endl;
#ifdef CGAL_LINKED_WITH_TBB
// Construct the locking data-structure, using the bounding-box of the points
auto bounding_box_size = static_cast<double>(timeslices+1);
Delaunay::Lock_data_structure locking_ds(
CGAL::Bbox_3(-bounding_box_size, -bounding_box_size, -bounding_box_size,
bounding_box_size, bounding_box_size, bounding_box_size), 50);
Delaunay universe(K(), &locking_ds);
#else
Delaunay universe;
#endif
auto universe_ptr = std::make_unique<decltype(universe)>(universe);
auto causal_vertices = make_foliated_sphere(simplices, timeslices);
insert_into_triangulation(universe_ptr, causal_vertices);
fix_triangulation(universe_ptr);
// This isn't as expensive as it looks thanks to return value optimization
return universe_ptr;
} // make_triangulation()Fast foliated Delaunay Triangulations in CGAL
256 timeslices, 222,132 vertices, 2,873,253 faces, 1,436,257 simplices
Creation time: 284.596s
(MacBook Pro Retina, Mid 2012)
Remaining Work
Interested? Please Join!
Thank You!
[1] The CGAL Project. CGAL User and Reference Manual. CGAL Editorial Board, 4.6.3 edition, 2015.
[2] Steve Carlip. Why Quantum Gravity is Hard. Conceptual and Technical Challenges for Quantum Gravity, Rome, September 2014.
[3] J. Ambjorn, J. Jurkiewicz, and R. Loll. “Dynamically Triangulating Lorentzian Quantum Gravity.” Nuclear Physics B 610, no. 2001 (May 27, 2001): 347–82.
[4] Rajesh Kommu. “A Validation of Causal Dynamical Triangulations.” arXiv:1110.6875, October 31, 2011. http://arxiv.org/abs/1110.6875.
Causal Dynamical Triangulations with CGAL Adam Getchell acgetchell@ucdavis.edu University of California, Davis CGAL Developers Conference, Nancy, Sept 29-October 2, 2015
Causal Dynamical Triangulations with CGAL
By Adam Getchell
Causal Dynamical Triangulations with CGAL
- 557
