Quantum Approximate Optimization Algorithm
How it works
Quantum evolutiom
Thetas are optimized (somehow)!
Quantum annealing
Step 1.: write as a HOBO
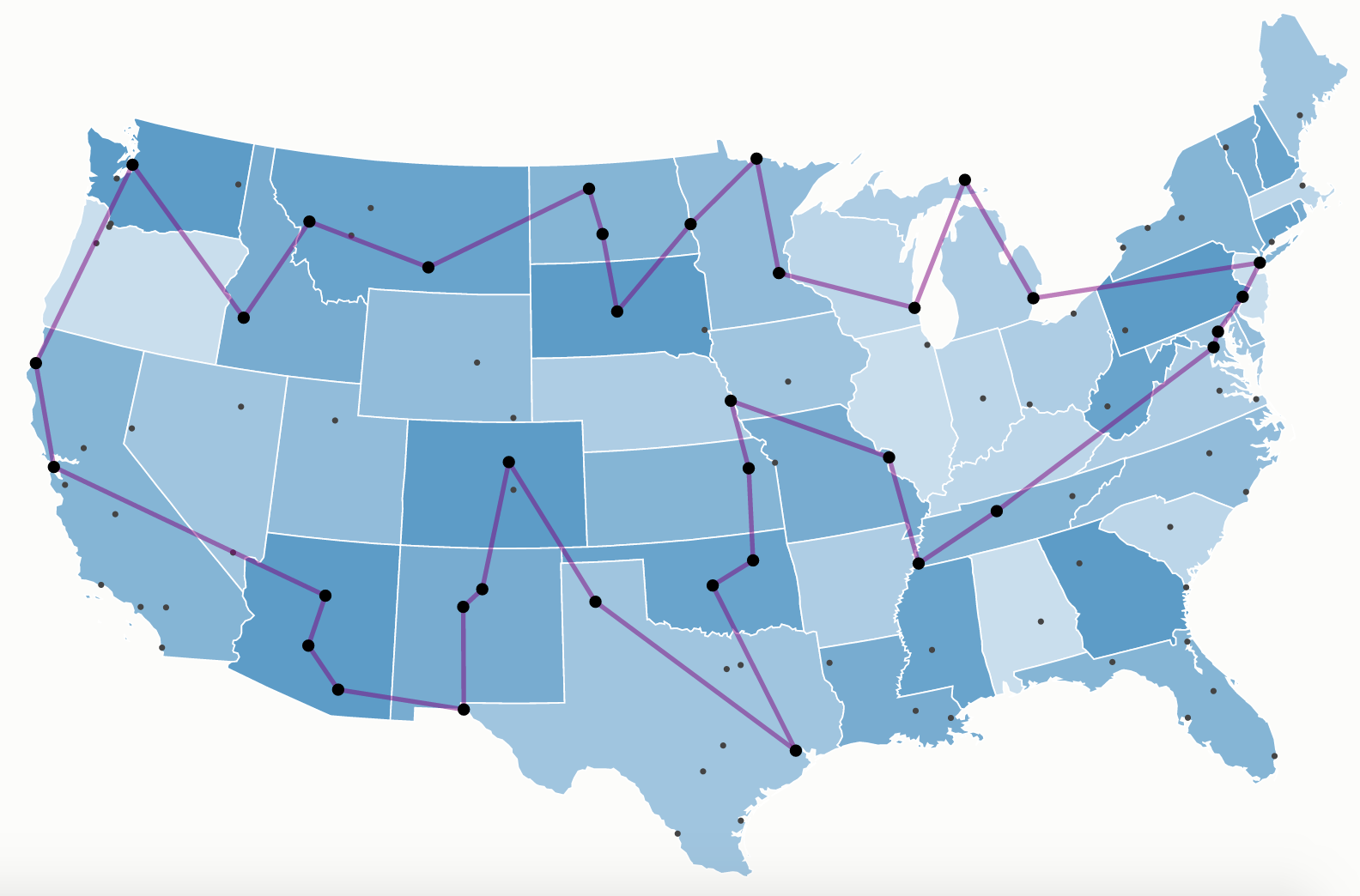
A sum of constraints and objective hamiltonians
Need to choose proper values A_1, A_2, B.
Quantum annealing
Step 2.: turn into a 2-local Ising model
Alternatively turn to QUBO and then to 2-local Ising model
non unique!
New qubits!
Quantum annealing
Step 3.: fit to interaction graph

J_{ij} != 0 iff s_i and s_j are connected - more qubits needed!
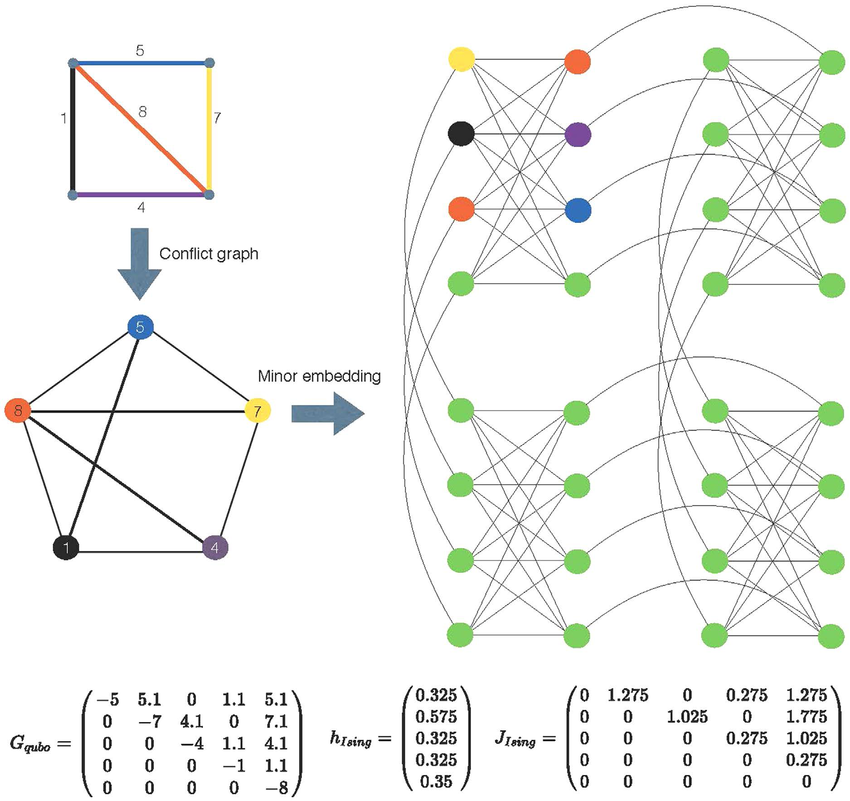
Quantum annealing
Conclusions
- D-Wave technology requires 2-local interactions following special topology (Chimera, Pegasus)
- Thus many qubits are required
- As long as we can write as HOBO (and we can fit it) we can run it (the whole procedure is known)
QAOA
Step 1.: write as a HOBO

A sum of constraints and objective hamiltonians
Need to choose proper values A_1, A_2, B.
QAOA
Step 2.: turn into a Ising model
No extra qubits needed in principle!, however there may be more nonzero terms
QAOA
Step 2a.: how to implement mixer
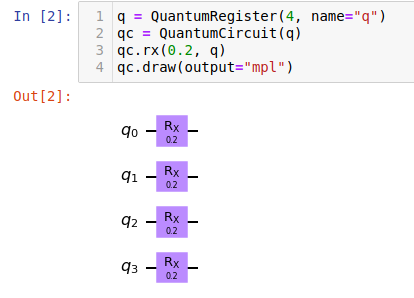
Always commuting!
QAOA
Step 2b.: how to implement obj. Ham.
Always commuting!
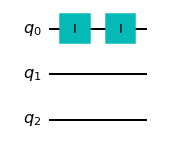
QAOA
Step 2b.: how to implement obj. Ham.
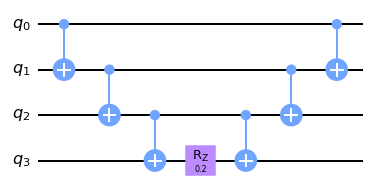
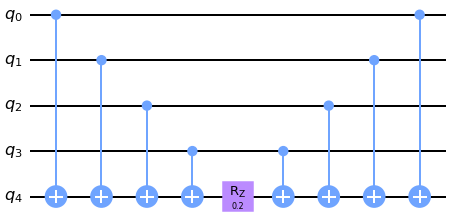
Extra qubit needed but CNOT-s commutes!
Note that not all qubits may be connected for QC as well - but we can SWAP
QAOA
Step 3.: run the optimizer
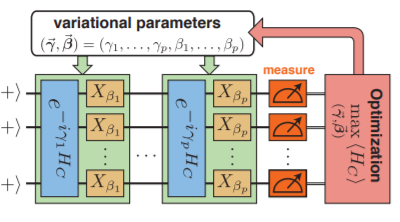
Depending on classical algorithm we use we may need:
- Estimate energy (simple)
- Estimate gradient (harder but manageable)
- Estimate Hessian (super-hard)
The more derivatives we know - usually the better the algorithm works
Math
We need to estimate the energy of the state given Hamiltonian
Measurement
0100100...10
Hamiltonian
The mean of energies E_i is expectedly the correct energy
Math
We may need to estimate the gradient
First way: calculate from the definition of gradient based on
Problem:
One can choose a different linear combination of energies for different thetas, however then the time complexity grows
Math
Energy estimation techniques
Hence we can estimate energy for each P_i independently.
2. Since all P_i commute, we can estimate energy based on bit-strings coming out from measurement.
NISQ assumptions
- QC are noisy (we are not able to implement exactly the unitary gate)
- Measurements are noisy (outputs, and by this energies are not always reliable,
- We don't have much qubits
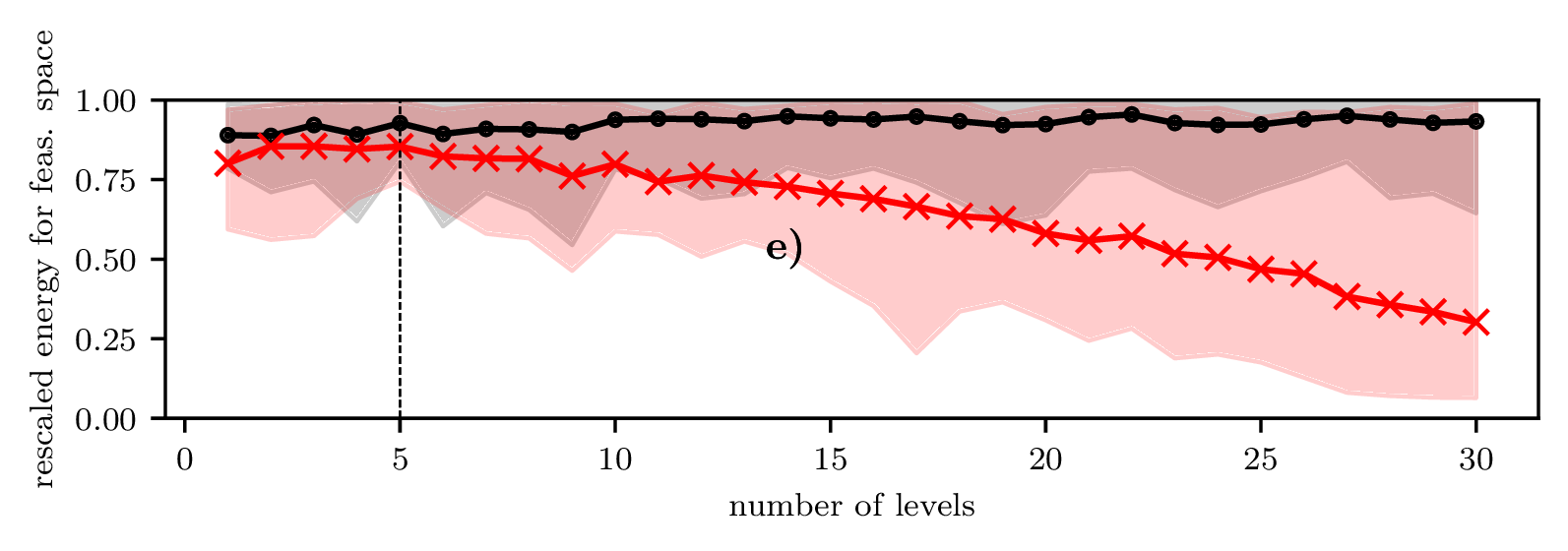
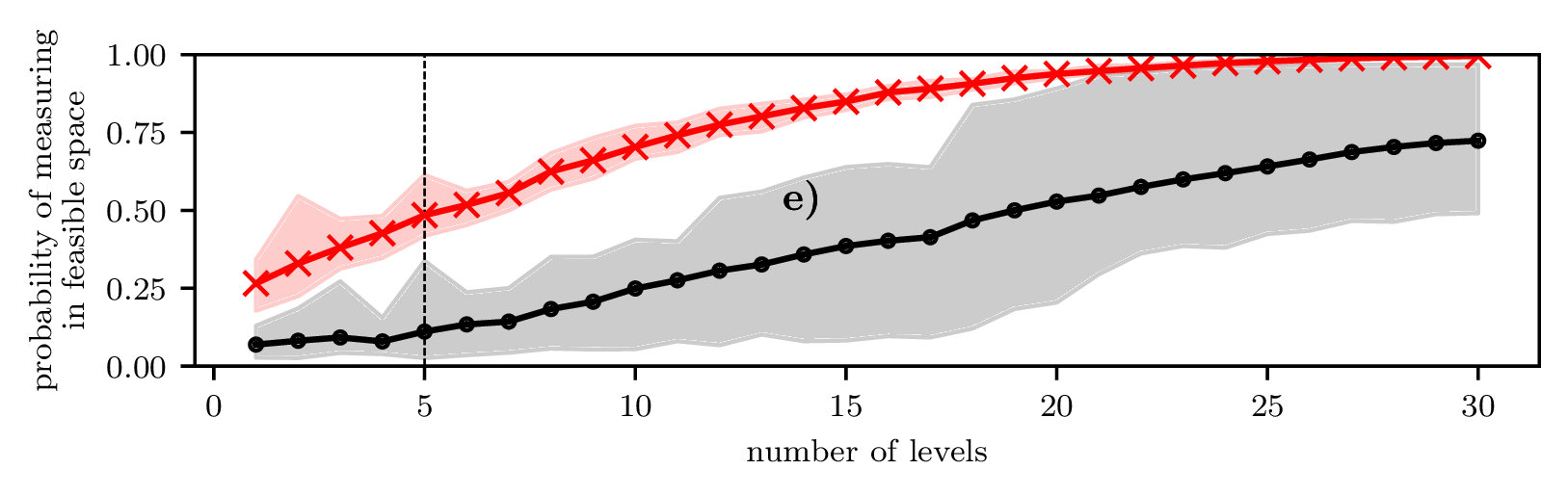
QAOA simulations
Levels of simulation truth
1. Calculate |phi> and then classicaly calculate <phi|H|phi>
"fast", but completely unphysical
2. Calculate |phi>, then make measurements and estimate energy
perfect but super slow
3. Calculate (noisy) |phi>, then make (noisy) measurement and estimate energy



slow, physical, but not NISQ-y
Order of ZZ...Z
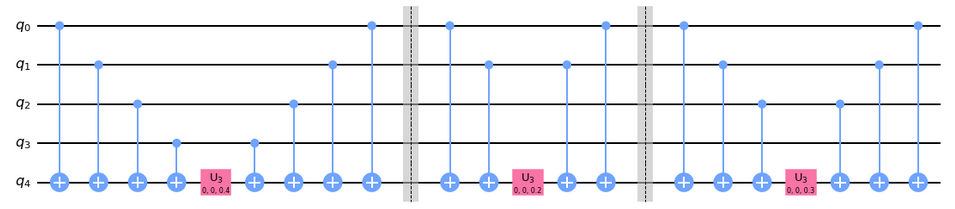
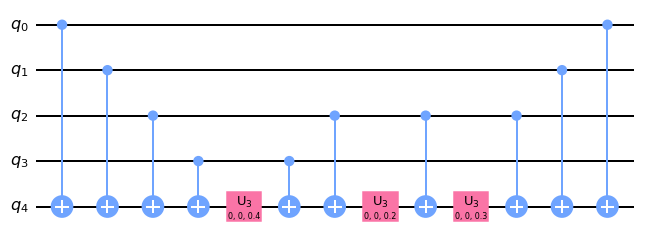
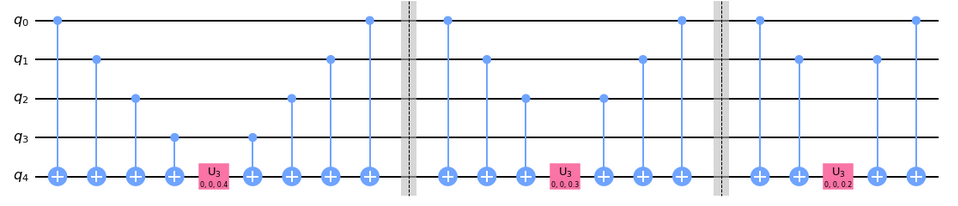
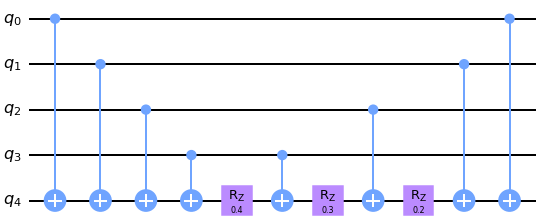
What kind of quality measures can we have?
- Number of qubits (super important!)
- Depth of the circuit (super important!)
- Number of Pauli terms (important!)
- noise robustness (important)
- Number of QC run/measurements

depth
Thank you!

Something extra
QAOA
By Adam Glos
QAOA
- 314



