Space-efficient binary optimization for variational computing
Adam Glos, Aleksandra Krawiec, Zoltán Zimborás
Institute of Theoretical and Applied Informatics, Polish Academy of Sciences
The problem: TSP
given the cost between cities, find the cheapest route such that the route goes through all cities and comes back
We need short, mathematical, and general description
Integer programming?
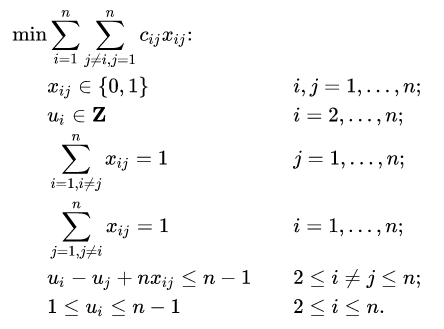
Quadratic Unconstrained Binary Optimization
f(b)=\sum_{i,j} Q_{i,j} b_ib_j+ C
Any NP-complete problem can be turned into QUBO
Every binary function can be turned into a polynomial, but not necessarily quadratic!
f:\{0,1\}^n \to \mathbb R
A\sum\limits_{v} \left( 1 - \sum\limits_{t} b_{tv} \right)^2 + A \sum\limits_{t} \left( 1 - \sum\limits_{v} b_{tv} \right)^2 + B \sum\limits_{\substack{v,w\\v\neq w}} W_{vw} \sum\limits_{t} b_{tv}b_{t+1,w}
\sum_{I\subseteq \{1,\dots,n\}} \alpha_I \prod_{i\in I} b_i
Lucas, Andrew. "Ising formulations of many NP problems." Frontiers in Physics 2 (2014): 5.
Ising model - the quantum way
0,1 => 1,-1
finite order => small model
QUBO => 2-local Ising model
b_i \leftarrow \frac{1-s_i}{2}
s_i \leftarrow Z_i
\sum_{I\subseteq \{1,\dots,n\}} \alpha_I \prod_{i\in I} b_i
\sum_{I\subseteq \{1,\dots,n\}} \tilde \alpha_I \prod_{i\in I} Z_i
\sum_{I\subseteq \{1,\dots,n\}} \tilde \alpha_I \prod_{i\in I} s_i
This is not true in general
b_1b_2\cdots b_n \to \frac{1}{2^n} (1-s_1) \cdots (1-s_n)
QAOA - a special gate-model QA
We can use higher-order terms
|++\ldots + \rangle
\exp(-\mathrm i r_{i}\sum_i X_i)
\exp(-\mathrm i p_i H_{\rm obj})
i \leftarrow i+1
| \varphi(p,r) \rangle
|
Farhi, Edward, Jeffrey Goldstone, and Sam Gutmann. "A quantum approximate optimization algorithm." arXiv preprint arXiv:1411.4028 (2014). |
b_1\cdots b_k
What if we have quite good quantum computers, but with very small number of qubits?
TSP - waste of qubits
We have n! possible routes
\log_2(n!) \sim n \log n
only n log(n) qubits! (but needs higher-order terms)
n^2
QAOA - can we run it?
H_{\neq}^{\rm HOBO}(b,b') = H_\delta^{\rm HOBO}(b,b') \coloneqq \prod\limits_{k=1}^K (1- (b_k - b'_k)^2)
H_{\rm valid}^{\rm HOBO}(b_t) \coloneqq \sum\limits_{k^0\in K_0} b_{t,k_0}\prod\limits_{k=k^0+1}^{K-1} (1-(b_{t,k} - \tilde b_{k})^2)
HOBO of order ~log(n) but still a small number of terms!
A_1\sum\limits_{t} H_{\rm valid} (b_t) + A_2\sum\limits_{t} \sum\limits_{t'\neq t} H_{\neq}(b_t,b_{t'}) +
+ B\sum\limits_{\substack{v,w\\v\neq w}} W_{vw} \sum\limits_{t}
H_\delta (b_t,v)H_\delta (b_{t+1},w)
(constraints)
(objective)
QAOA - can we run it? cont.
\exp(-\mathrm i \alpha Z_1 Z_2 Z_3) ?
\exp(-\mathrm i (\alpha_1 Z_1 Z_2 Z_3+ \alpha_2 Z_1Z_2 )) \\=
\exp(-\mathrm i \alpha_1 Z_1 Z_2 Z_3 ) \exp(-\mathrm i \alpha_2 Z_1 Z_2 )
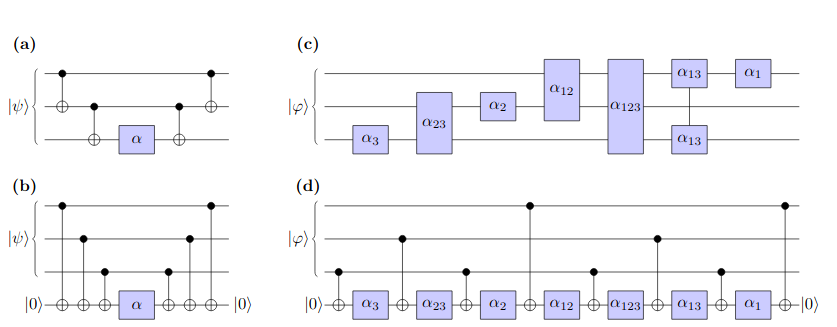
QAOA - can we run it? cont.
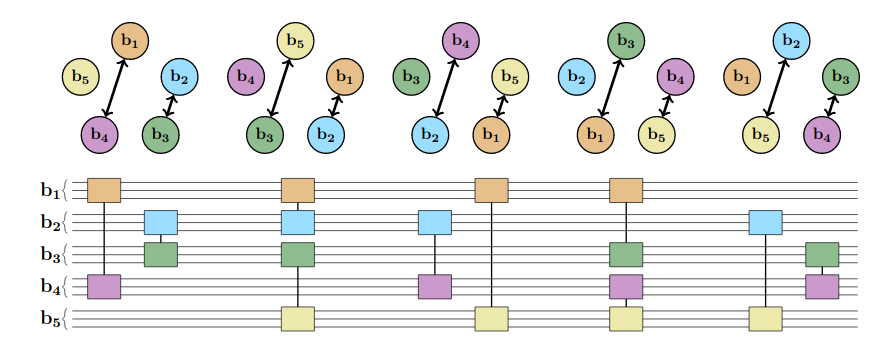
round robin-tournament
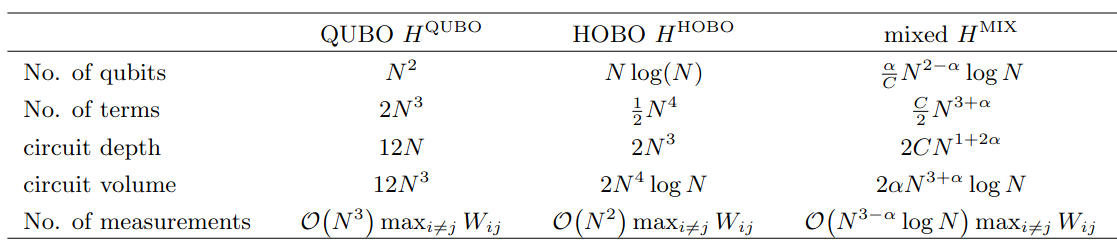
Is HOBO better?
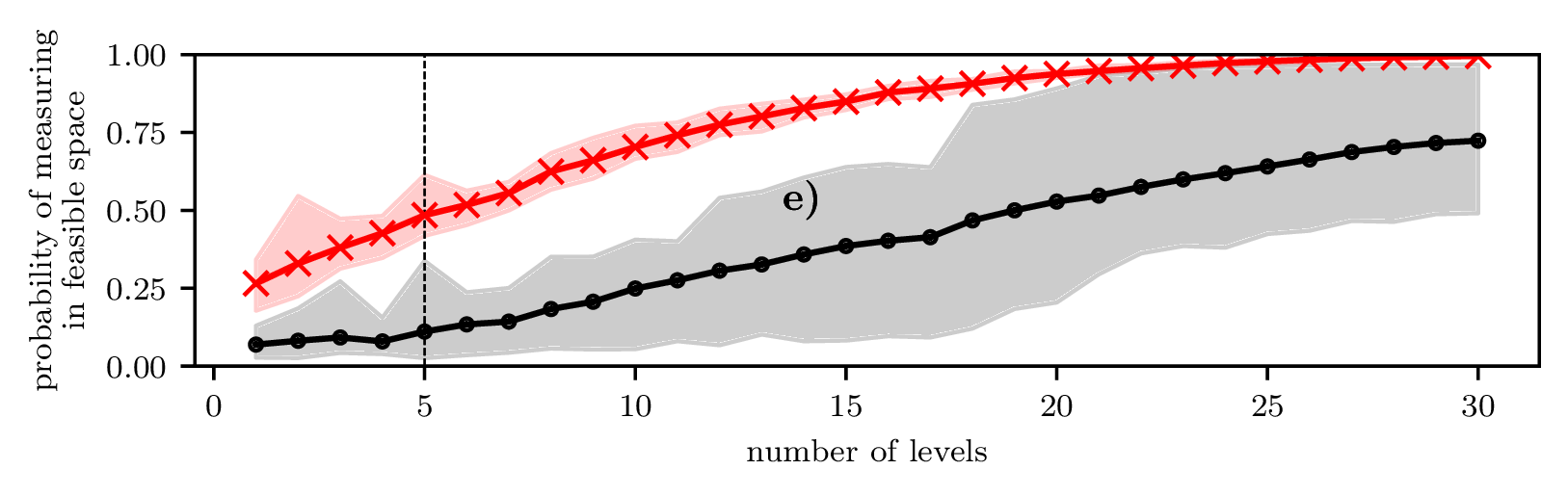
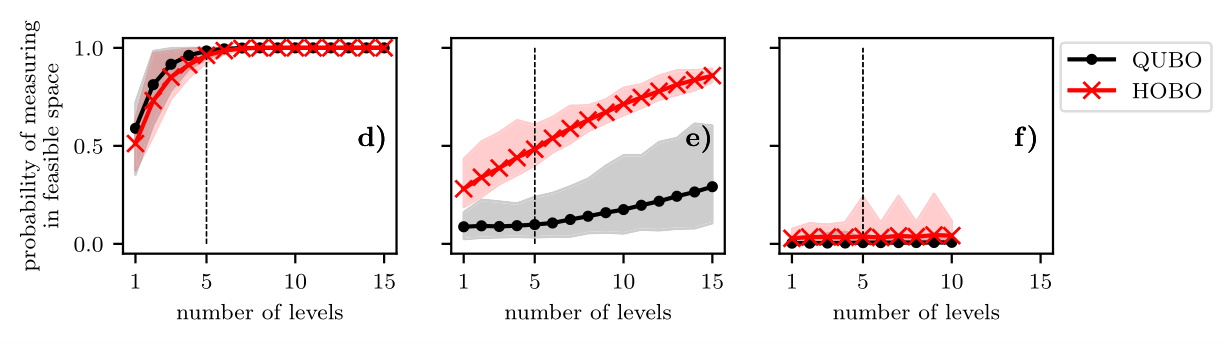
N=3
N=4
N=3
N=5
N=4
Text
depth
no. qubits
n^2
n^3
n
n\log n
HOBO
QUBO
Text
?
Intermediate cases?
Good mixed approach
0 \rightarrow 01\,00
1 \rightarrow 10\,00
2 \rightarrow 11\,00
3 \rightarrow 00\,01
4 \rightarrow 00\,10
5 \rightarrow 00\,11
n^{1+2\alpha}
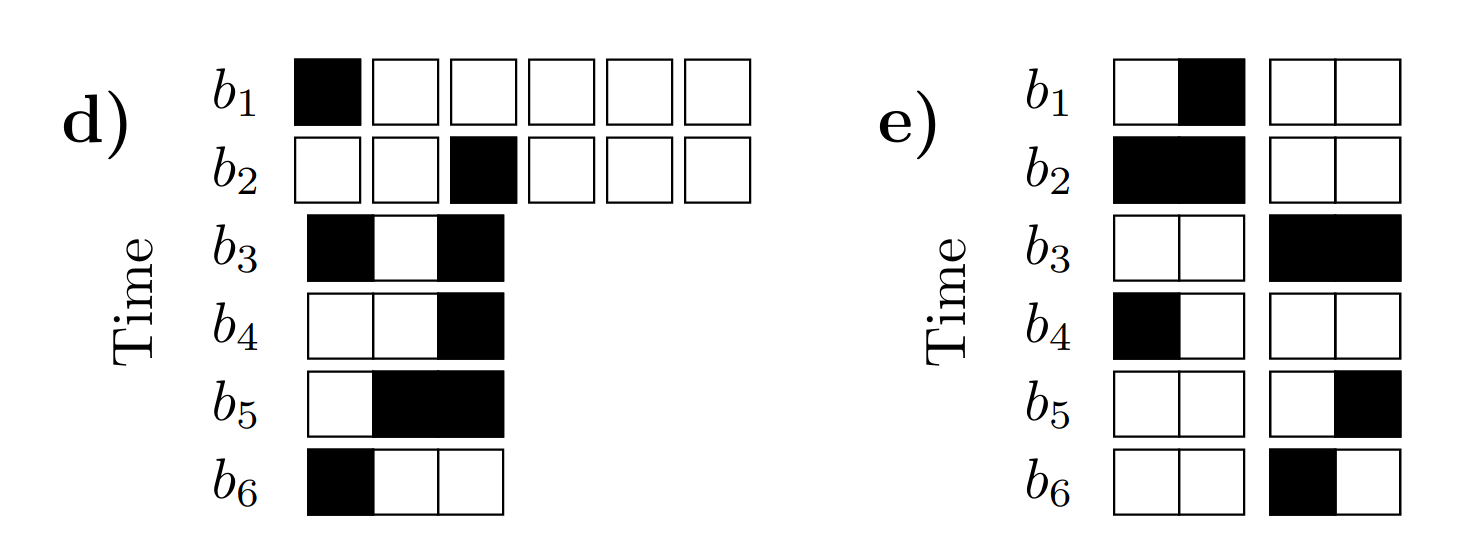
HOBO
QUBO
n^{1-\alpha}\log n
Conclusions
- smaller number of qubits,
- (probably) more efficient than QUBO + QAOA,
- has smaller relative feasible space,
- produces MUCH deeper circuits than QUBO!
Glos, A., Krawiec, A., & Zimborás, Z. (2020). Space-efficient binary optimization for variational computing. arXiv preprint arXiv:2009.07309.
Also true for Quantum Alternating Operator Ansatz
New idea!
Today, 15:40 GMT!
HOBO-size mixer
QUBO objective encoding
|+\rangle
\theta
\Huge \dagger
|\varphi(\theta,\theta')\rangle
\theta'
|00\ldots0\rangle
|00\ldots0\rangle
Change of the encoding (from binary to one-hot vector at inverse)
QAOA Quantum science days 01.06.2021
By Adam Glos
