Constrained Delegation
Lessons for Behavioral Mechanism Design
University of Californa, Riverside
March, 2026
Brandon Williams
Alistair Wilson
Richard Van Weelden
Setup
- Tend to get inefficiency when we consider interactions between uninformed and informed parties:
- Sender-receiver
- Bargaining
- Market for lemons
- In some of these settings, delegating decision power to the informed party:
- Potential for efficient solution
- But share of surplus created is smaller for the party ceding power
Motivation
Constrained Delegation allows for an intermediate outcome:
- The uninformed party delegates some of their decision power to the informed party
- But imposes some constraints on the choices the informed party can make
- For example, minimum and maximum limits
Veto bargaining provides an economically important setting to examine this:
- Veto represents an outside option
- Theory identifies constrained delegation as optimal mechanism (Kartik, Kleiner, and Van Weelden, 2021)
- Simple setting for a clear experimental assessment!
Setup
Consider the following bargaining context:
- Nature determines the informed party's preference
- An uninformed principal makes a proposal
- An informed agent responds, comparing the offer it to her outside option




Findings
- Comparing Constrained Delegation to Take-it-or-Leave it offers we find:
- Constrained delegation does increase efficiency a lot
- However, the informed party still captures almost all of the benefits behaviorally
- Proposers fail to optimize the design problem over delegation, providing more latitude/discretion
- Pre-play communication yields similar gains across mechanisms
Literature
Models of similar bargaining forms have been proposed in theory...
- Under complete information - Romer and Rosenthal (1978)
- Under cheap talk negotiation - Matthews (1989)
- With valuable expertise involved - Holmström (1977, 1984)
- More recently: Kartik, Kleiner, Van Weelden (2021)
And used in experiments...
- Early bargaining - e.g. Roth and Murnighan (1980, 1982)
- Vetoes within committees - Kagel, Sung, and Winter (2010)
- Multiple rounds of bargaining - Nunnari (2021)
More recently: Kartik, Kleiner, Van Weelden (2021)
Take a mechanism design approach to show when Proposer:
- Fully delegates
- Makes a take-it-or-leave-it offer
- Offers a choice with constraints

Theory
Theory
Theory
0
1
Theory

Proposer
0
1
Theory

Proposer
0
1
- Proposer has:
- Increasing payoff \( \pi (z) \) over the outcome \( z \)
- for simplicity, we'll assume \(\pi(z)=z\)
- Will make an offer to the vetoer
- Increasing payoff \( \pi (z) \) over the outcome \( z \)
Theory


Vetoer
0
1
Proposer
\( \theta \)
- Veteor has:
- Ideal point \( \theta \) which is private information, \( \theta \sim F(\theta) \)
Theory


???
0
1
\( \theta \)
- Veteor has:
- Ideal point \( \theta \) which is private information, \( \theta \sim F(\theta) \)
Theory


???
0
1
- Veteor has:
- Ideal point \( \theta \) which is private information, \( \theta \sim F(\theta) \)
- Preference represented by convex loss from ideal \(\theta\)
- Takes choice \( z \in \{0,y\} \): either the veto threat point (here 0) or the offer \(y\).
\( \theta \)
Theory


0
1
- Veteor has:
- Ideal point \( \theta \) which is private information, \( \theta \sim F(\theta) \)
- Preference represented by convex loss from ideal \(\theta\)
- Takes choice \( z \in \{0,y\} \): either the veto threat point (here 0) or the offer \(y\).
Theory: Take it or Leave It
0
1
Proposer
Offer \( y \)
\( \frac{ y}{2} \)
These types veto
These types take offer
\( z = 0 \)
\( z = y \)
Theory: Take it or Leave It
0
1
Proposer
Offer \( y \)
\( \frac{ y}{2} \)
Suboptimal deals:
inefficient as \( \theta > y \)
preferred by both
Breakdown:
inefficient as \( \theta > 0 \) preferred by both
Theory: TIOLI equilibrium
- Proposer increasing the offer \(y\) leads to:
- Marginal gain of \(\pi'(y)\cdot(1-F(\tfrac{y}{2}))\)
- Marginal loss of \(\left(\pi(y)-\pi(0)\right)\cdot \tfrac{1}{2}f(\tfrac{y}{2})\)
0
1
\(\tfrac{y}{2}\)
\(z=0\)
\(z=y\)
\(y\)
\(f(\theta)\)
Theory: TIOLI equilibrium
0
1
\(\tfrac{y}{2}\)
- Proposer increasing the offer \(y\) leads to:
- Marginal gain of \((1-F(\tfrac{y}{2}))\)
- Marginal loss of \(\tfrac{y}{2}\cdot f(\tfrac{y}{2})\)
\(z=0\)
\(z=y\)
\(y\)
\(f(\theta)\)
Theory: Delegation
0
\( \theta \)
1
Vetoer ideal
Proposer
- Proposer:
- Offers set of options \(Y\)
- Vetoer has:
- Chooses \(z\in\left\{0\right\}\cup Y\), either the veto threat point (here \(0\)) or some offer in delegation set
Theory: Delegation
0
1
\( \frac{ y}{2} \)
These types veto
These types
choose minimum offer
\( z = 0 \)
\( z = y \)
Offer \( [y,1] \)
\( y \)
These types
choose their ideal point
\( z = \theta \)
Theory: Delegation
0
1
\( \frac{ y}{2} \)
Offer \( [y,1] \)
\( y \)
No suboptimal deals:
The delegation mechanism ensures
these options are available
Breakdown:
inefficient as \( \theta > 0 \)
Theory: Delegation Equilibrium
- Proposer increasing the minimal offer \(y\) leads to:
- Marginal gain of \(\pi'(y)\cdot(F(y)-F(\tfrac{y}{2}))\)
- Marginal loss of \(\left(\pi(y)-\pi(0)\right)\cdot \tfrac{1}{2}f(\tfrac{y}{2})\)
0
1
\(\tfrac{y}{2}\)
\(y\)
\(f(\theta)\)
Theory: Delegation Equilibrium
0
1
\(\tfrac{y}{2}\)
\(y\)
\(f(\theta)\)
- Proposer increasing the offer \(y\) leads to:
- Marginal gain of \((F(y)-F(\tfrac{y}{2}))\)
- Marginal loss of \(\tfrac{y}{2}\cdot f(\tfrac{y}{2})\)
Theory: Delegation Equilibrium
0
1
\(\tfrac{y}{2}\)
\(y\)
\(f(\theta)\)
- With increasing density we get a corner solution:
- coincide with TIOLI solution, \(y^\star=1\)
Theory: Delegation Equilibrium
- With decreasing density we get the other corner solution:
- Full delegation, with \(Y^\star=\Theta\) and \(z^\star=\theta\)
0
1
\(\tfrac{y}{2}\)
\(y\)
\(f(\theta)\)
Theory: Summary
- Delegation should substantially reduce inefficiency
- Remove all the suboptimality by providing choice
- By changing the margins, leads to more latitude in offers, so decreasing breakdown too
- Delegation should improve the proposer's payoffs
- Proposers offers should shift with the distribution of responders
Theory: Environment Characteristics
- Delegation here is for compromise over veto threat:
- Proposer has state-independent preferences
- Tension is over the use of the veto/failure to agree
- This is not Delegation over information a la Holmstrom (1984)
- Expert has valuable information for Proposer's state-dependent preference
- Tension is over expert's preference misalignment
Theory: Hypotheses
- Delegation improves Proposer outcomes over TIOLI
- Delegation is:
- Full delegation with decreasing density
- No compromise with increasing density
- Constrained with unimodal density
- Proposer provides increased discretion as Proposer's risk aversion increases
- Cheap talk is:
- Informative in the TIOLI set-up (Matthews QJE 1989)
- Uninformative with used Delegation (Kartik et al AER 2021)
Experiment
Experimental Design
- Construct environment that directly follows the veto-bargaining framework
- One challenge: how to bring this abstract environment to a participants in a way that is easier to understand?
Experimental Design
- Construct environment that directly follows the veto-bargaining framework
- One challenge: how to bring this abstract environment to a participants in a way that is easier to understand?




Experimental Design
- Construct environment that directly follows the veto-bargaining framework
- One challenge: how to bring this abstract environment to a participants in a way that is easier to understand?




Experimental Design: Framing
Proposer
Seller
Vetoer
Buyer
State
Ideal Demand
Offer
Widgets
Delegation
Widget Menu
Types
Urn Draws
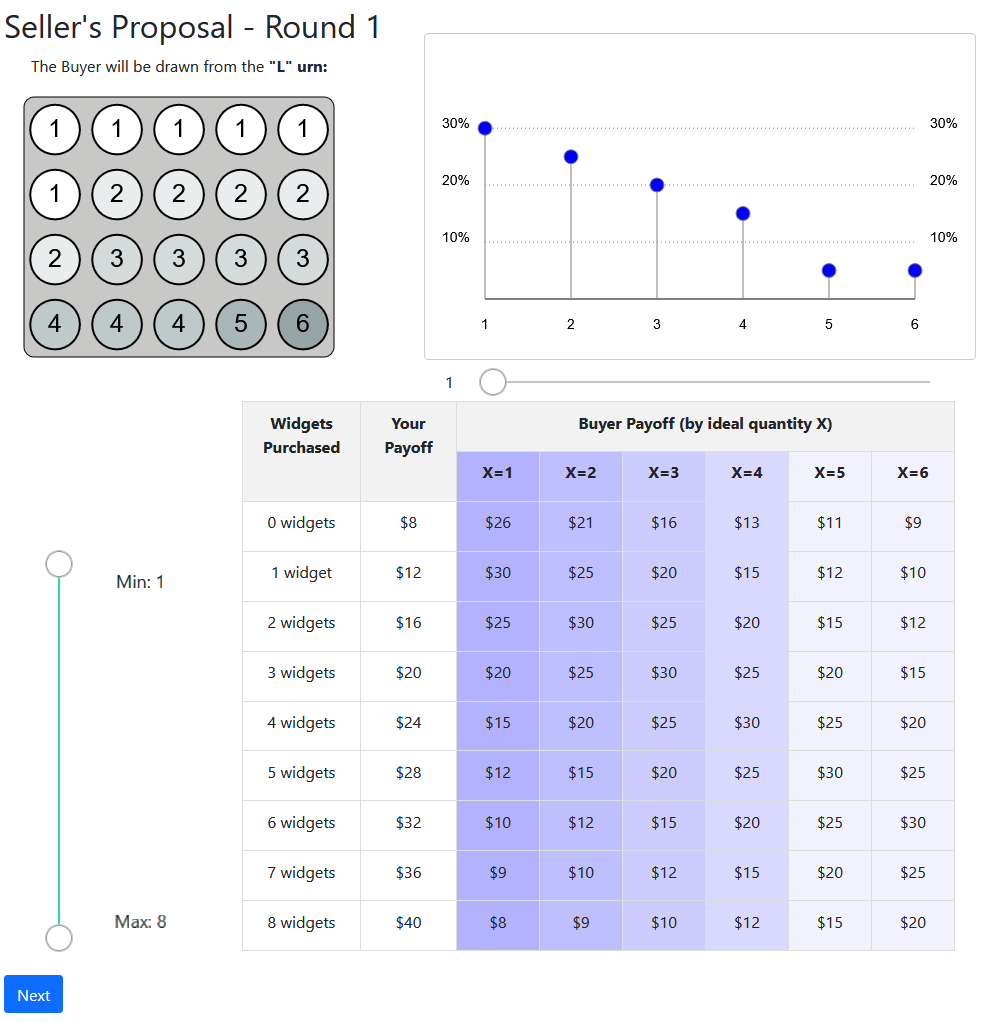



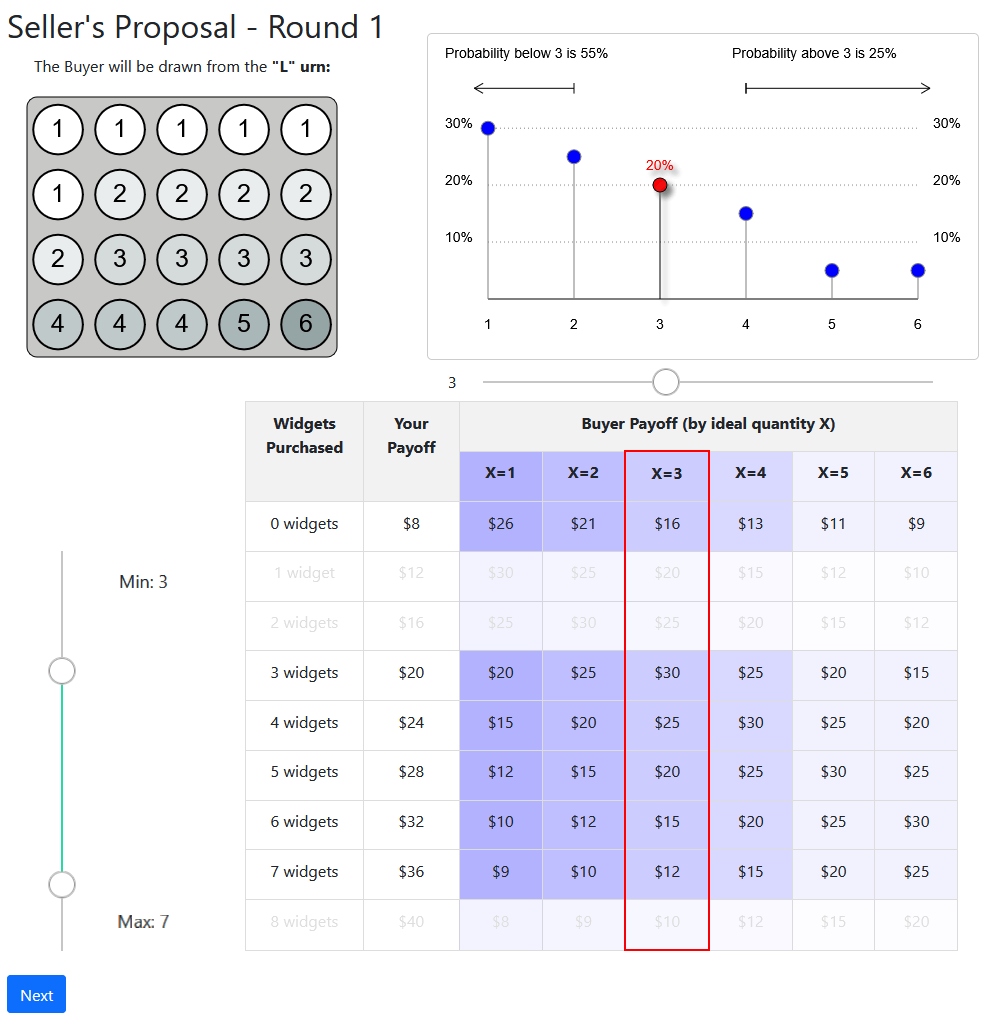
Delegation treatment:
offer a range
Take it or leave it:
single offer

Decreasing
probability
Inverse-U shaped
Increasing probability
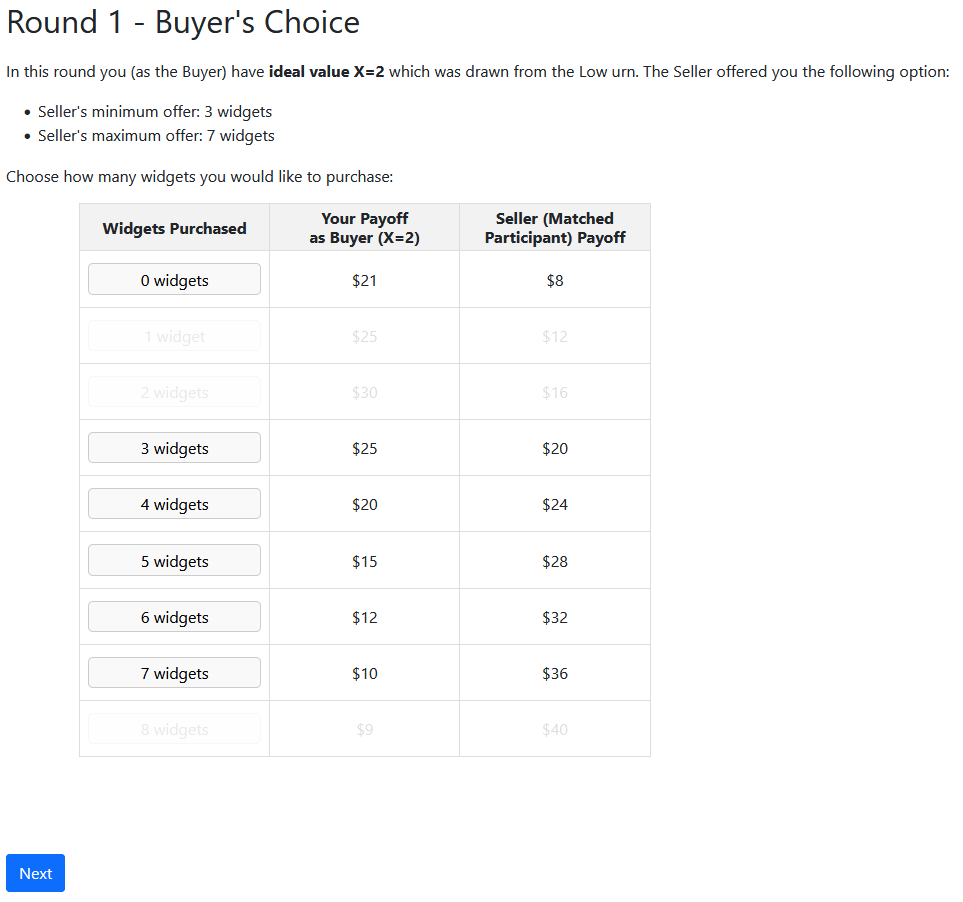
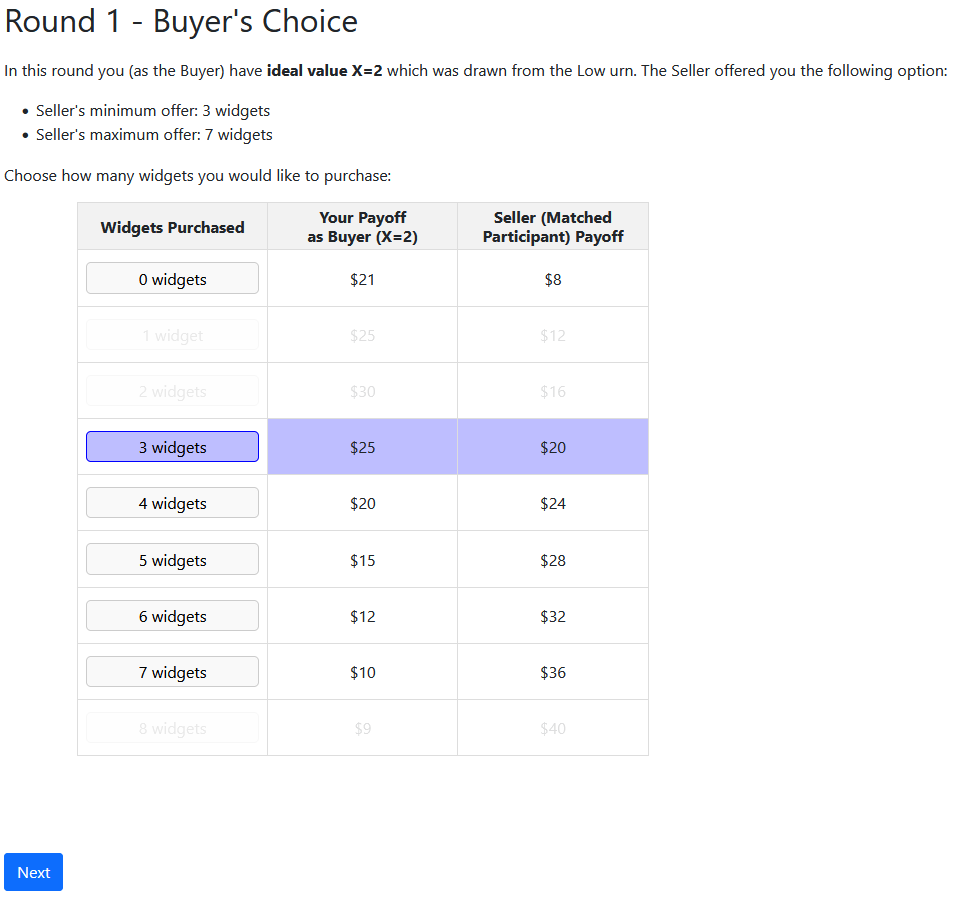

Experimental Design
- Within-subject variation:
- Varying distributions (high, middle, low) for the Buyer
- Changing roles: 5 rounds in one role, 5 rounds in the other, and back to first role for 5 more rounds
- Between subject 2 x 2:
| No Chat | Chat | |
| Take-it-or-leave-it | N=66 | N=60 |
| Delegation | N=64 | N=66 |
Experimental Design
- Within-subject variation:
- Varying distributions (high, middle, low) for the Buyer
- Between subject 2 x 2
- Collect other behavioral variables (identification through subtraction):
- Robot Buyer: remove strategic uncertainty/other regarding
- Pure incentives: present mechanism choice as lottery (remove mechanism complexity)
- Pure allocation: remove uncertainty and mechanism
Experimental Predictions
-
Varying distributions for the Buyer ideal provide a sanity check on understanding
- Full Delegation with decreasing density
- No Delegation with increasing density
- Conditional Delegation predicted to:
- substantially increase efficiency
- increase Seller payoff (relative to TIOLI)
- discretion increases with Seller risk aversion
- Communication before the game:
- Partial improvements in TIOLI
- No effect in Delegation
Results



Low
Middle
High
Sanity check: Sellers respond to alignment

Sanity check: Sellers respond to alignment
Low
Middle
High



Minimal offer in interval:
Sanity check: Sellers respond to alignment
Low
Middle
High



Minimal offer in interval:
Sanity check: Sellers respond to alignment
Low



Middle
High
Sellers offer more latitude under delegation
Other quick results
- Buyers overwhelmingly pick the best option available
- They pick the best number of widgets from the menu, and take the outside option when better
- Sellers (mostly) keep offers higher than the minimum
- They mostly refrain from modifying the upper bound

Model of Buyer Behavior
- Large majority (~90%) of Buyer decisions are selfish/rational
- The remaining 10% are inefficient, but tend to choose more generously for Sellers
- Estimate a model of Buyer behavior to integrate out exogenous shocks
Model of Buyer Behavior
- Fehr-Schmidt parameterized logit model for Buyer behavior:
\(U_B(x_B,x_S)=\lambda \cdot x_1 - \alpha\cdot \max(x_S-x_B,0) - \beta\cdot \max(x_B- x_S ,0) \)
Here express relative parameters:
- Relative effect of disadvantageous inequality: \(\tfrac{\alpha}{\lambda}\)
- Relative effect of advantageous inequality:\(\tfrac{\beta}{\lambda}\)
| Param | TIOLI | Delegation |
|---|---|---|
| Disad. Inequality | 0.08 | 0.43 |
| Adv. Inequality | 0.20 | 0.17 |
Using model allows us to integrate out exogenous shock \(\theta\) when forming expectations
Efficiency of Outcomes
Delegation should increase efficiency
Take it or Leave It
Delegation

Delegation should increase efficiency
Take it or Leave It
Delegation

Take it or Leave It is inefficient
Take it or Leave It
Delegation

Inefficiency not eliminated under delegation
Take it or Leave It
Delegation

Delegation does increase efficiency
Take it or Leave It
Delegation

Take it or Leave It
Delegation

Delegation does increase efficiency
Result 1:
Conditional Delegation drastically increases efficiency in our experiments relative to Take-it-or-leave-it offers.
Distribution of Outcome
Who benefits from delegation?

Low
Who benefits from delegation?

Middle
Who benefits from delegation?

High
Result 2:
Efficiency gains from Conditional Delegation yields more gains for Buyer (though this mirrors the theoretical predictions). When Seller has more bargaining power, Conditional Delegation backfires.
Replace Buyers with Selfish Player
Replace Buyers with selfish Robots?

Replace Buyers with selfish Robots?

Replace Buyers with selfish Robots?

What explains behavioral deviations?
Additional treatments at the end:
- Replace Buyer with a payoff-maximizing Robot player
- Remove strategic uncertainty and other-regarding concerns
- Maintain Robot, but remove mechanism framing
- Remove complexity, pure choice over lotteries
- Pure other-regarding decision
- Remove risk, purely distributive decision
Robot Buyer
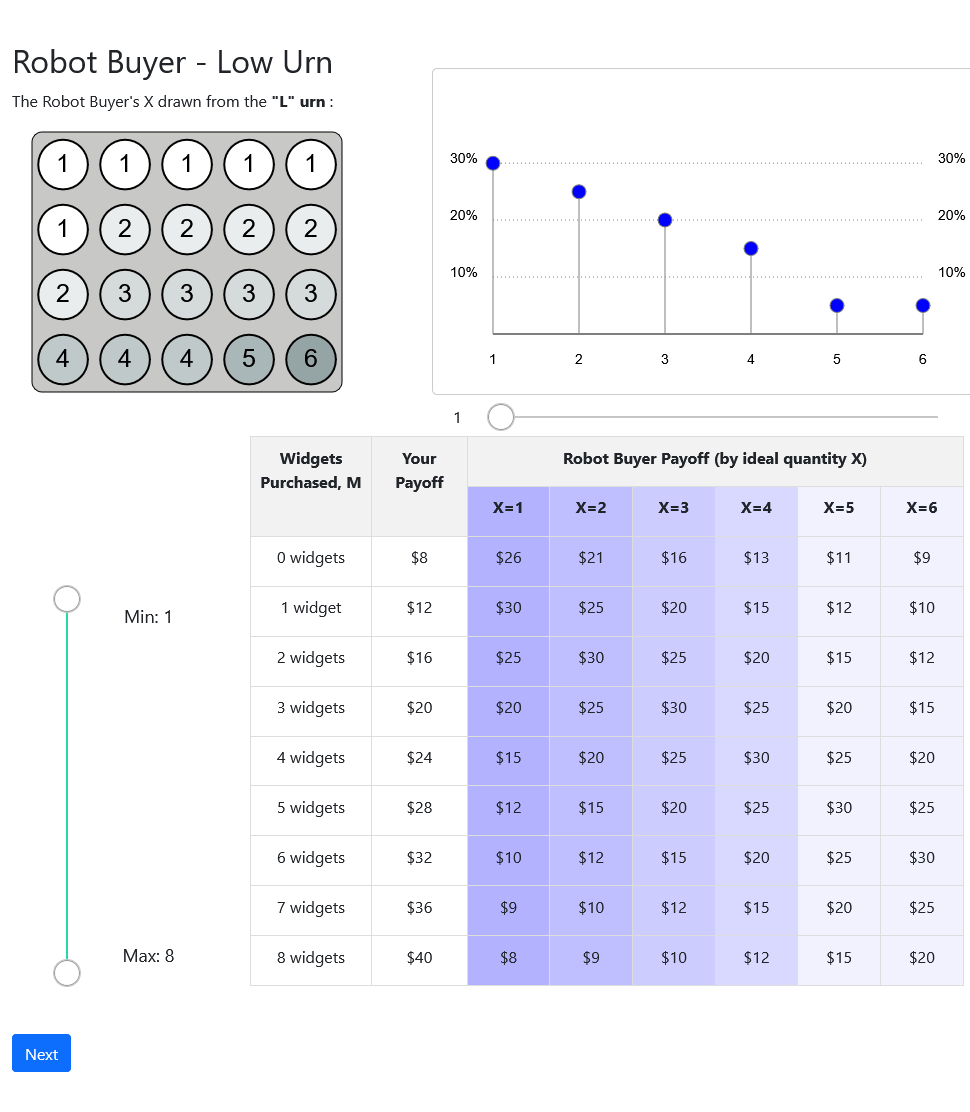
- Same decision screen/interface
- Same payoffs
- Repeat for all three urns
Remove mechanism framing
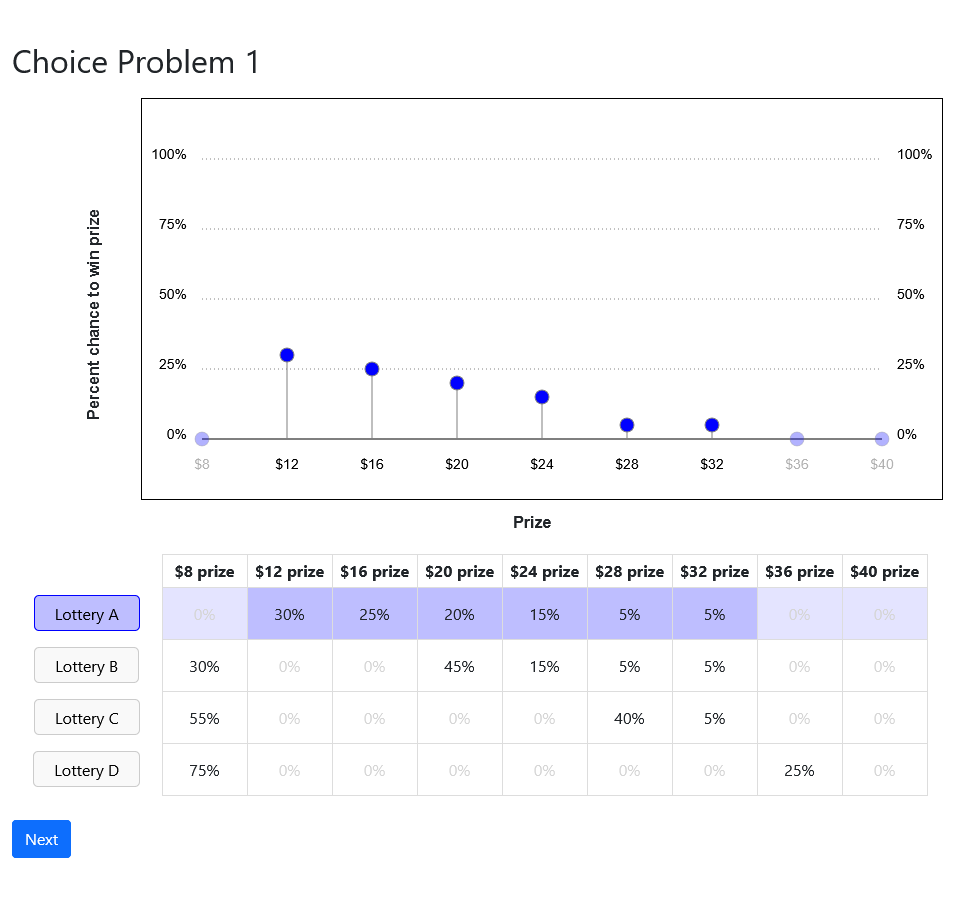
- Choices are lotteries
- Each lottery option corresponds to delegation decision
- Do this for all three urns
- For TIOLI and Delegation
Self/Other Distribution Choice
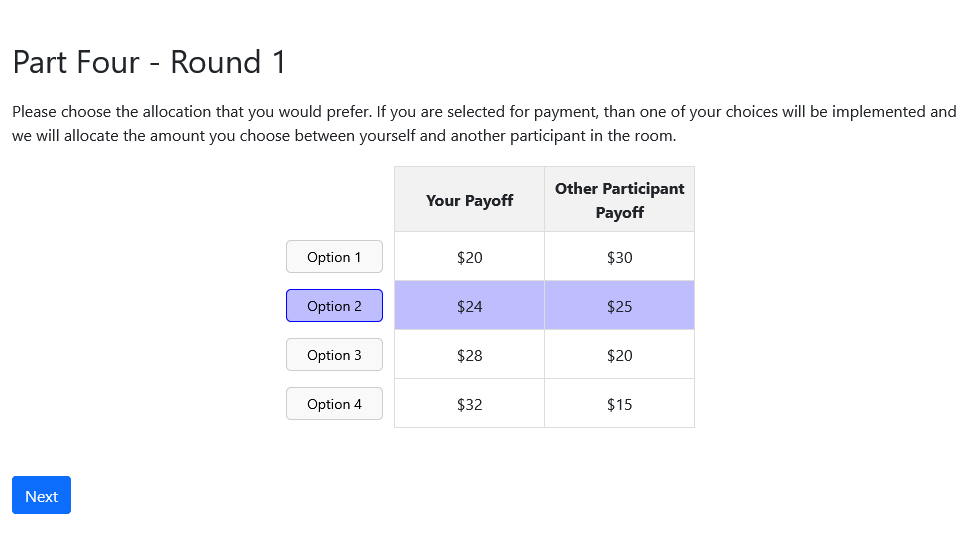
- Fix unknown state, look at dictator problem for Sellers
- Repeat this for low/med/high states
What explains behavioral deviations?



What explains behavioral deviations?



Main reason sellers don't extract more of the delegation gain is optimization failure:
- Remove player: Robot choices closely match delegation choices
What explains behavioral deviations?



- Remove player: Robot choices closely match delegation choices
- Remove mechanism complexity: Lottery choices indicate pure preference is for less delegation
Replace delegation decisions with lottery?

Replace delegation decisions with lottery?

Replace delegation decisions with lottery?

Replace delegation decisions with lottery?
- Sellers do better with Conditional Delegation when presented as pure lottery
- Do not find any substantive difference for TIOLI
- Suggests an optimization failure over the mechanism
Delegation discretion and Risk Pref.?






Low
Middle
High
Results: Key Points
- Offers respond to the expected type in a well-ordered manner
- Sellers offer more latitude than theoretical prediction
- Sellers in delegation offer ever more latitude
- Delegation mechanism is more efficient than take it or leave it
- Responds to Seller risk preferences, no effect in TIOLI
- Most of the "cost" of the mechanism falls on the Seller:
- More of the efficiency gains are captured by the Buyer
- Best improvements for the Seller is when alignment is low
- Data suggest that the optimization failures are a reason for greater latitude in delegation
Pre-play Communication


Theory: Communication
- For TIOLI, partially informative
- Two vague messages
- High/Low
- For Delegation, no gain over conditional delegation
- Only useful for No Compromise outcome (High urn)
Results: Chat
Seller: What are you willing to buy? Buyer: A middle number will work for me Seller: Okay, which is better, three or four Buyer: 3
- TIOLI, \(\theta=3\), Middle urn
- Offer is \(y=4\)
- Outcome \(z=4\)
Results: Chat
Buyer: 0-4 or i walk Buyer: simple Seller: hehe Buyer: ok ok Seller: 2-4? Buyer: so what u gonna offer Seller: hows that bud Buyer: hows what bud Seller: 2-4
- Delegation, \(\theta=3\), Middle urn
- Offer is \(Y=[2, 4]\)
- Outcome \(z=3\)
Results: Chat
Buyer: i got 1 Seller: hi Buyer: pls help me out Seller: ok ok Buyer: tyyy Seller: i got you Buyer: :) Seller: :)
- Delegation, \(\theta=2\), Low urn
- Offer is \(Y=[1, 6]\)
- Outcome \(z=2\)
Results: Inefficiency (Data with No Comm)

TIOLI
Delegation
Results: Inefficiency (Data with Comm)

Results: Communication
- Still a lot of work to do with the communication data
- Cannot integrate out Buyer state realization as this is potentially revealed during conversation
- We use Gemini 3 to code the chats:
- Across treatments Buyers reveal their ideal:
- 69% in TIOLI (no effect by \(\theta\))
- 42% in Delegation (decreasing in \(\theta\))
- Sellers concede 41% of the time to Buyer ideal
- More haggling by Seller in TIOLI
- Across treatments Buyers reveal their ideal:
- Still tuning some of the chat coding
Results: Seller Outcome (relative to full deleg)
| Dist. | TIOLI | Delegation |
|---|---|---|
| Low | -14% | +1% |
| Middle | -7% | +4% |
| High | +3% | -7% |
Without Chat:
| Dist. | TIOLI | Delegation |
|---|---|---|
| Low | +20% | +13% |
| Middle | +13% | 0% |
| High | +8% | +5% |
With Chat:
Conclusion
- Examine constrained delegation
- Here in an ideal setting (veto bargaining)
- Participants respond to key tensions from the theory
- Clear efficiency gains from delegation
- But more of the surplus goes to the responder
- An optimization failure in using the mechanism leads to over-delegation
- However, in expectation this error helps increase efficiency!
- Preplay communication leads to:
- Much greater efficiency in TIOLI
- Slight increase in efficiency for Delegation
- Additional tensions in communication
Thank you! 🙏
Questions or Comments?
Diagnosing the Failures: Pure Optimization
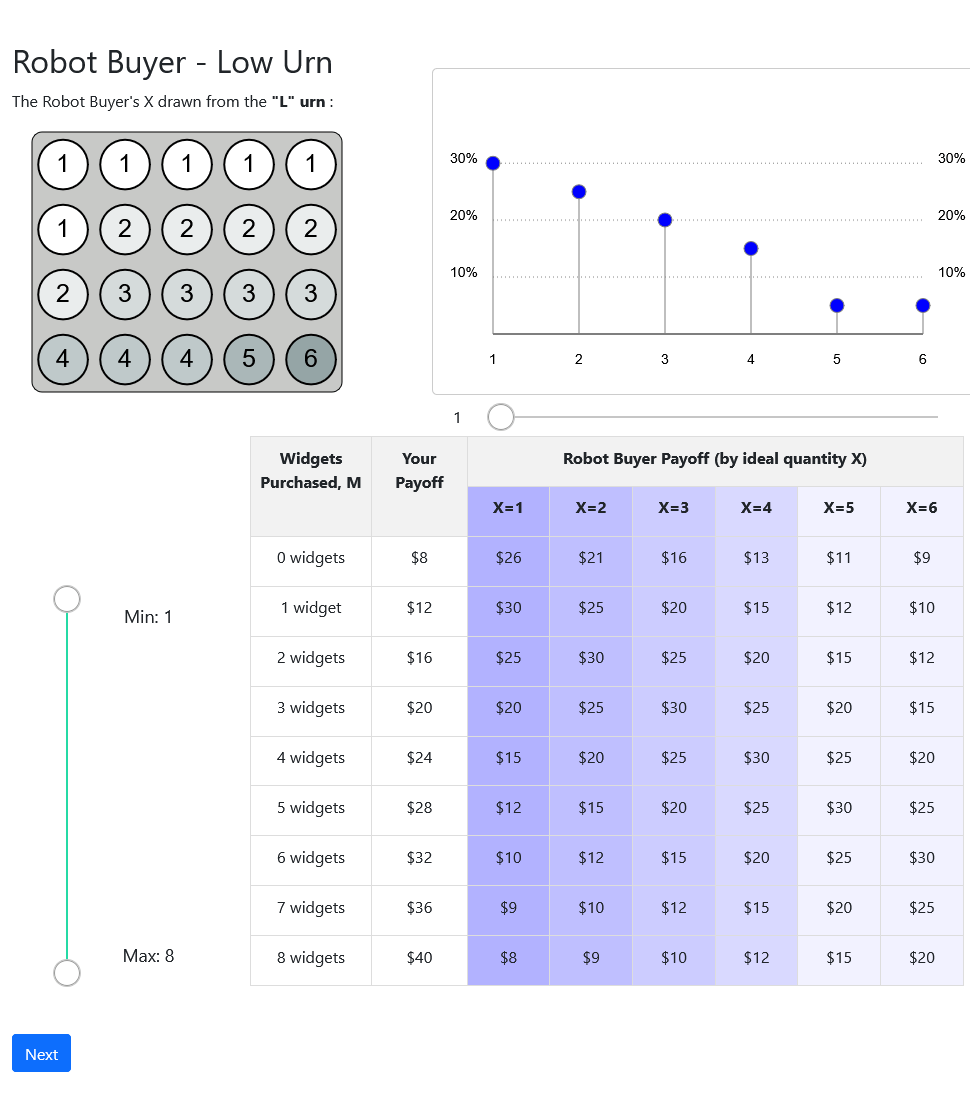
Diagnosing the Failures: Lotteries
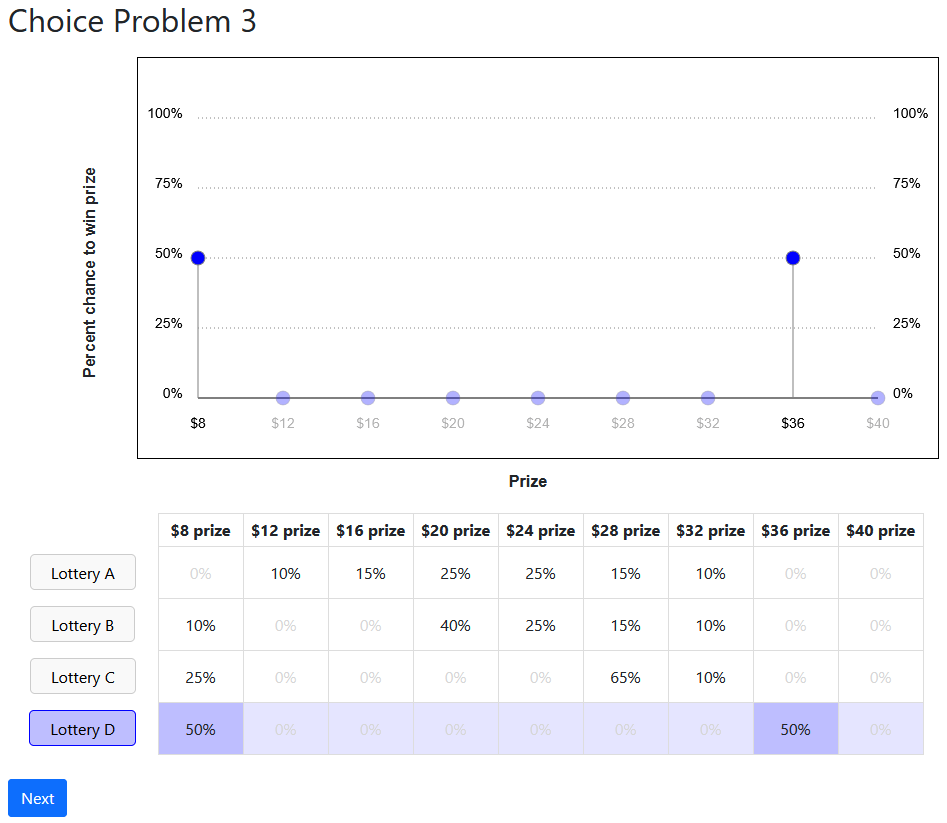
Diagnosing the Failures: Distribution
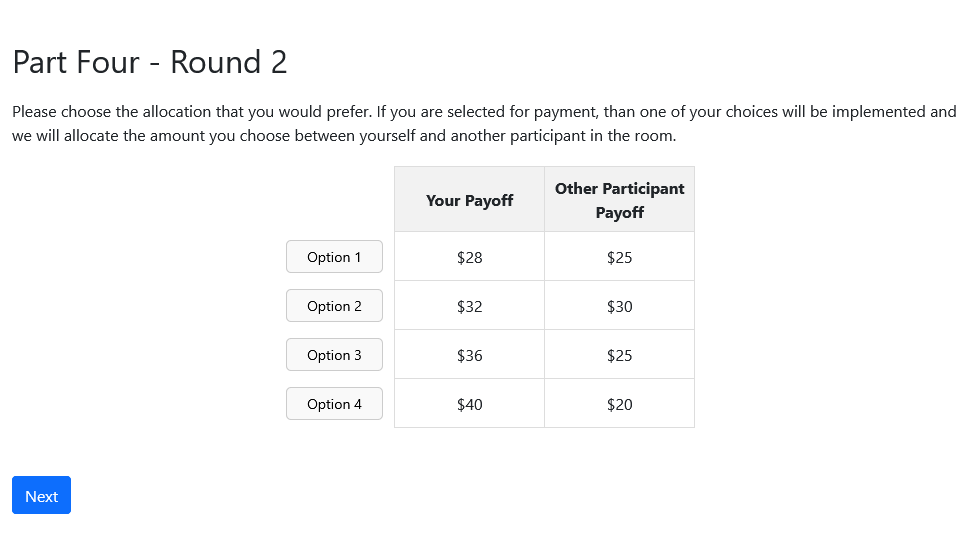
Constrained Delegation
By Alistair Wilson
Constrained Delegation
Exploring how the theory for Constrained Delegation maps to actual human behavior, and using this as one way of examining how behavioral agents might act when designing mechanisms.
- 119


