Costly Belief Elicitation
| Brandon Williams |
Alistair Wilson |
| Barcelona Summer Forum June 2025 |


An experimental testbed for understanding effort and incentive in belief elicitation
Intro/ Basic Idea
- Experimental economists commonly give incentives when we elicit beliefs. Why?
- Hope that by providing incentives we collect better, more-accurate beliefs:
- Understanding what is asked requires effort
- Overcome personal motives to distort
- Doing burdensome calculations
- Therefore, if belief elicitation is an effortful exercise, how do we best increase the precision of the expressed belief?
Want to understand what incentives produce honest, deliberative beliefs
Motivation
0
100
20
80
Want to understand what incentives produce honest, deliberative beliefs
Motivation
0
100
20
80
Project Roadmap
- Create a task that mirrors forming a probabilistic belief that requires effort and responds to incentives
- Use experiments on Prolific to understand the relationship between cost, effort, and output
- Vary the task primitives and measure how long it takes to complete (effort), willingness to accept (cost) and accuracy (output)
- Understand how hard this task is to guess (zero effort output)
- Then use the task with different incentives
- Bring this back to a common lab task
Literature
Some examples of recent papers in belief elicitation:
-
Testing incentive compatibility:
- Danz, Vesterlund, and Wilson, 2022
- Healy and Kagel, 2023
-
"Close enough" payments:
- Enke, Graeber, Oprea, and Young, 2024
- Ba, Bohren, and Imas, 2024
- Settele, 2022
-
QSR or BSR:
- Hoffman and Burks, 2020
- Radzevick and Moore, 2010
- Harrison et al., 2022
-
Others (exact or quartile):
- Huffman, Raymond, and Shvets, 2022
- Bullock, Gerber, Hill, and Huber, 2015
- Prior, Sood, and Khanna, 2015
- Peterson and Iyengar, 2020
Treatments
So far we have the following treatments:
- A calibration treatment where we measure how long it takes to complete the problem (Effort); and how accurate you are (Output), then elicit your willingness to accept payment for the task (Cost)
- An initial guess treatment where we measure your first instinct (low-effort output)
- Incentives treatments where we change the reward structure (horserace across incentives)
Basic Task
- Create a task that mirrors forming a probabilistic belief that requires effort
- What is the proportion of blue tokens in this urn?

Ans: 56.25%
- Create a task that mirrors forming a probabilistic belief that requires effort
- Use experiments on Prolific to understand the relationship between cost, effort, and precision
- Vary the cost for precision and calibrate on how long it takes to complete and willingness to accept (calibration treatment)
- Understand how hard this problem is to guess (initial guess treatment)
- Vary the reward structure (incentive treatments):
- BSR with no information
- BRR with qualitative information
- BSR with quantitative information
- A "close enough" incentive
Experimental task
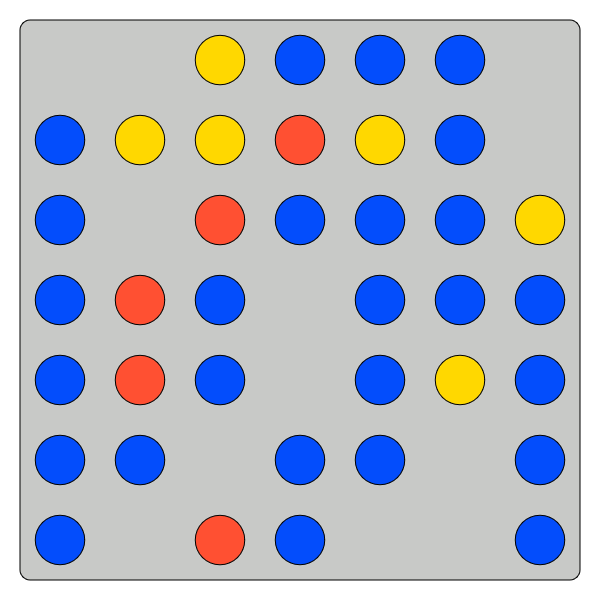
How to get you to exert effort when formulating your belief?
We start by paying $0.50 if you exactly count:
- Number of blue tokens
- Number of total tokens
Measure accuracy and time taken
Vary the difficulty over 5 tasks
Calibration: Training
Task Variance
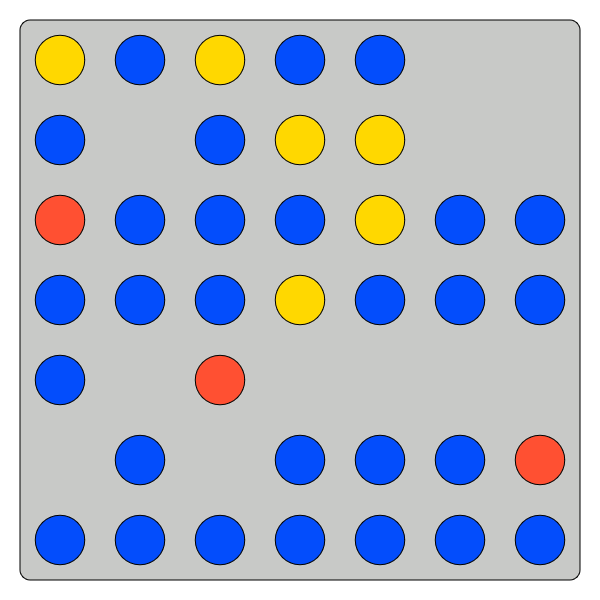



Small no gaps
Small gaps
Larger no gaps
Larger gaps
Task Variance

Each problem characterized by a tuple \(\left(\theta^\star,N,\delta_\text{Gaps}\right) \):
Core parameter:
- \(\theta^\star\) the true proportion of blue tokens
Cost Parameters to find \(\theta^\star\):
- \(N\): total number of tokens in urn
- \(\delta_{\text{Gaps}}\): indicator for gaps
\(\left(\theta^\star,N,\delta_\text{Gaps}\right) = (139 , \tfrac{81}{139},1) \)
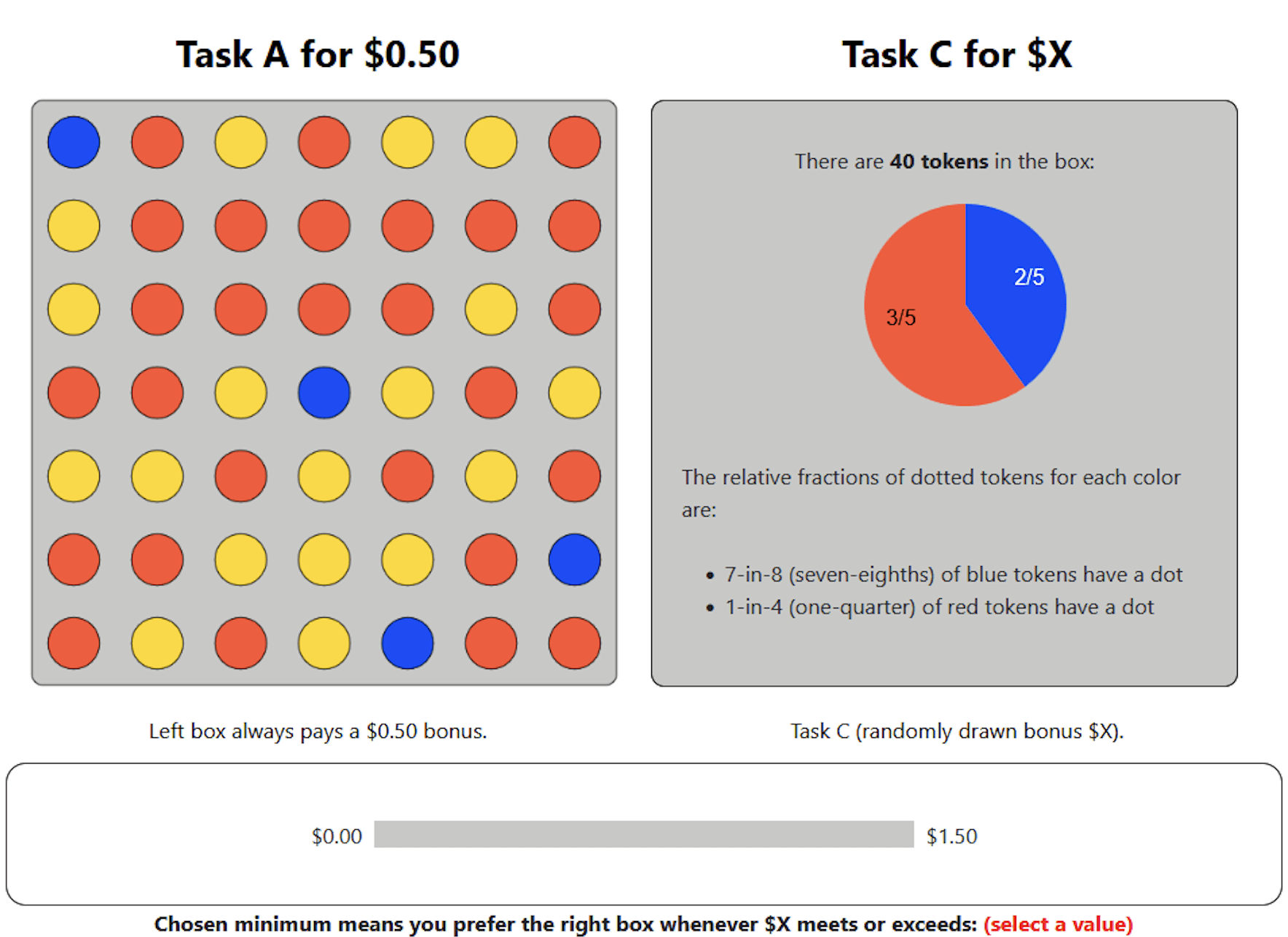
Willingness to Pay: Oprea (2020)
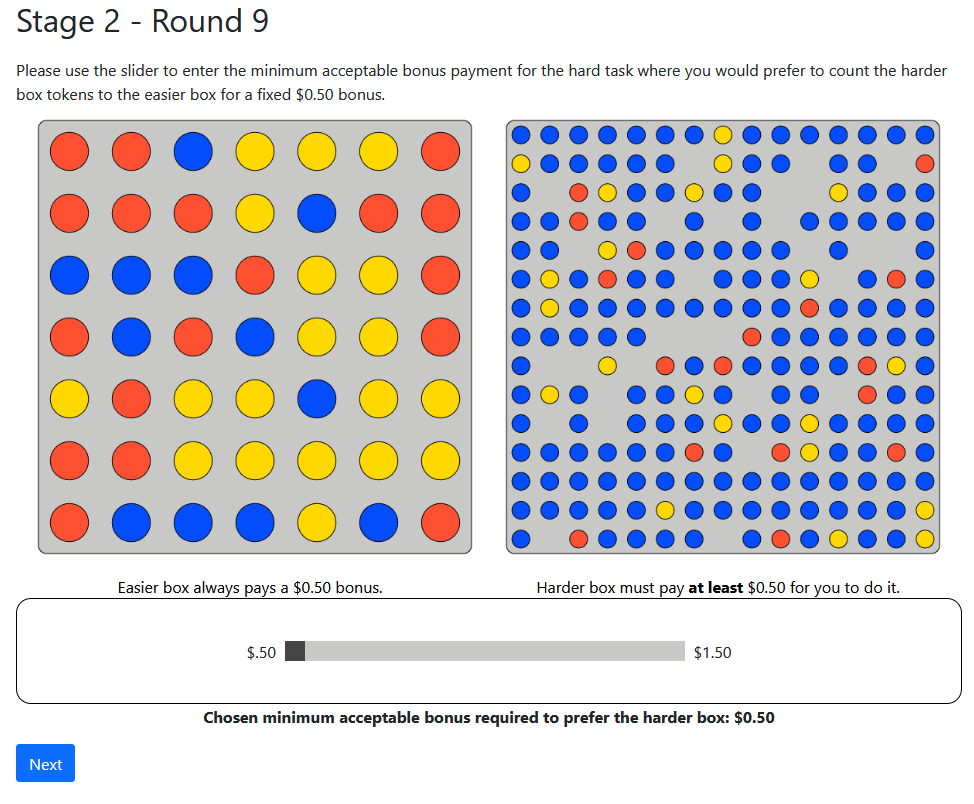
Ten rounds: An easy task, or a Hard one plus amount \(\$X\)
LHS:
Constant
Difficulty
RHS:
Varying
Difficulty
Always
Pays $.50
If Correct
$X
If Correct
Choose
$X threshold
Calibration Results (\(N=250\))
From models over \(\left(N,\delta_\text{Gaps}\times N\right) \)
\(\text{OLS }(\text{Effort})\)
\(\text{Tobit}(\text{WTA})\)
\(\text{Logit }(\text{Correct})\)

Output

Effort

WTA
Initial Guesses
Before we move to incentives, we also assess how hard this problem is to guess.
- Give them 15 or 45 seconds to form and enter a guess on the proportion
- Higher powered rewards:
- $2.50 if within 1%
- $1.00 if within 5%
- $0.50 if within 10%
- Ask them about 10 proportions (pay three decisions)
Initial Guess Results (\(N=200\))
After 15 second
After 45 second
Task Conclusions
- So we have an experimental task that:
- That responds to effort and incentives, where we can scale the difficulty
- We understand the effort required to succeed, and amount we need to pay people
- We can quantify the output at low-effort
Incentives
Use four incentives to ask about beliefs in ten different urns:
-
BSR-Desc: $1.50 prize with only qualitative information on the details
- Text description of payoff structure (Vespa & Wilson, 2018)
-
BSR-Inf: as above but with quantitative information
- Full information on the quantitative incentives (Danz et al., 2022)
- BSR-NoInf: only know there is a $1.50 prize, no other information on the incentives
- A "close enough" incentive
- $1.50 if within 1%; $0.50 if within 5%
- Current use in several papers (e.g. Ba et al., 2024)
- Pay three of the ten rounds
- \(N=100\) each incentive treatment
- No time limit
Model
- Agents know that there are \(N\) tokens in the urn, but are unsure about the blue proportion
- Initial prior on the number of blue tokens is \[\text{BetaBinomial}(1,1,N)\]
- Can choose to sample \(0 \leq n \leq N \) tokens without replacement from the urn (Hyper geometric signal)
- Counting \(k\) blue balls and \(n-k\) non-blue leads to posterior \[\text{BetaBinomial}(1+k,1+n-k,N-n)\]
- With this model we can calculate the expected return from counting \(n\) balls from \(N\) under a mechanism that incentivizes a report \(q\) with payment \(\phi(q)\)
Incentives to Exert Effort
Results
Output by difficulty
Using our calibration treatments to construct instruments for difficulty:
Effort by difficulty
Using our calibration treatments to construct instruments for difficulty:
Output: Accuracy
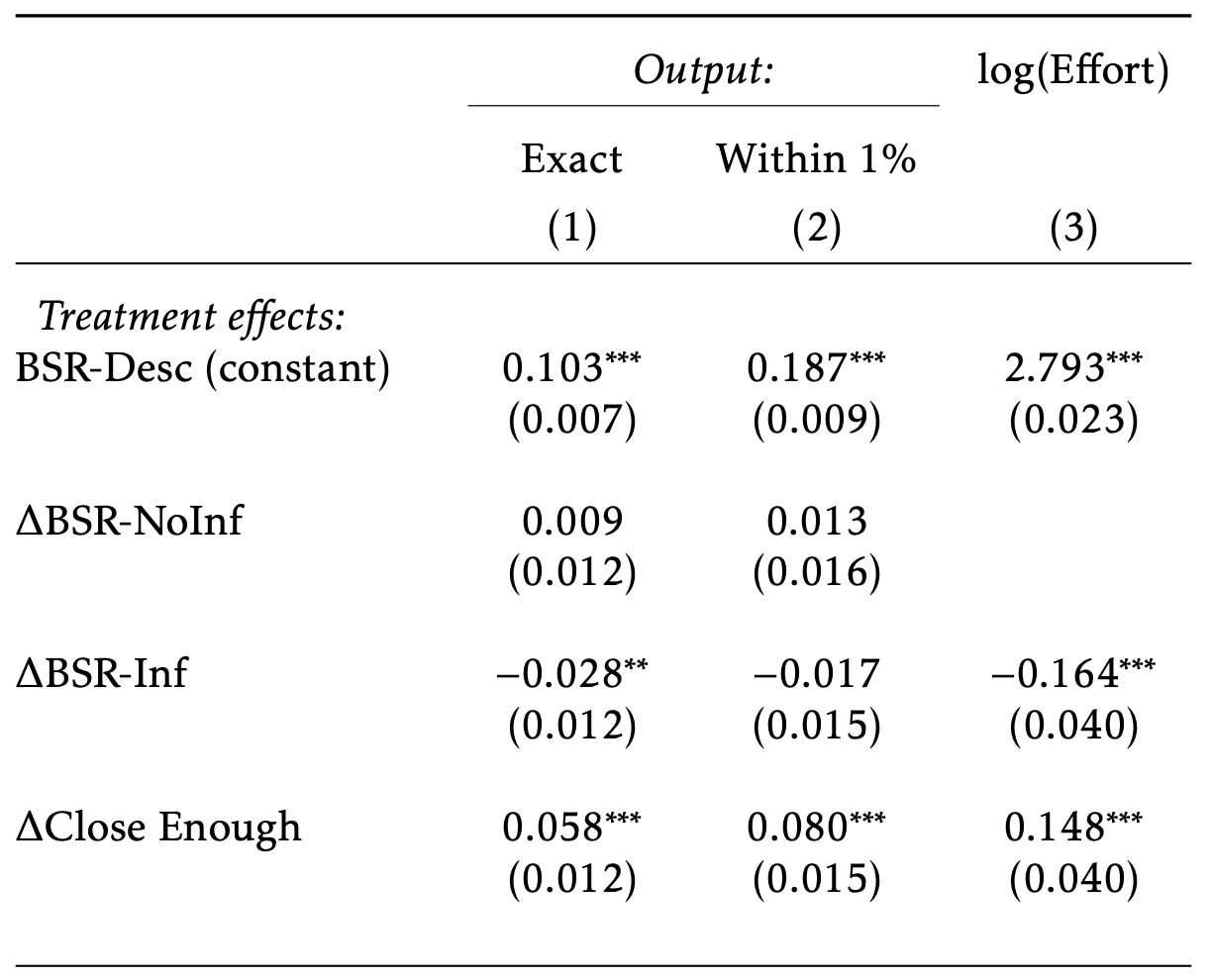
-15%
+16%
+56%
+43%
Effort compared to Calibration

Aside: Cognitive Uncertainty
Common self-reported measure, which here we validate against effort and output in BSR-NoInf treatment...
Incentive effects
- "Close enough" outperforms BSR on both accuracy and time spent
- The better incentive effects stemming from a richer outcome space
- Also cheaper for the experimenter, incentive payments to participants reduced by ~50% over BSR
- With a fixed budget, how much more effort could be induced?
- (But the gains here are dwarfed by the gains when we explicitly tell them what to do)
Incentive effects
Bayesian Updating
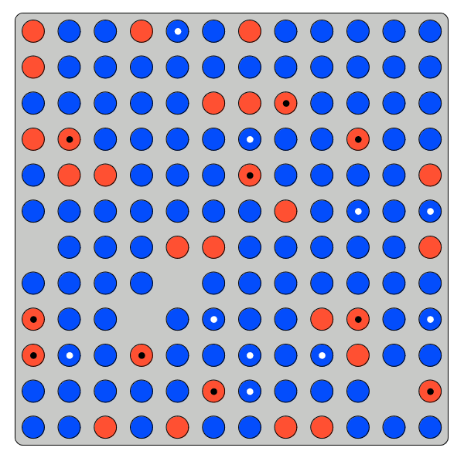
Participants told:
- Number of tokens
- Proportion blue
- Proportion Dots | Blue
- Proportion Dots | Red
Are then asked for the proportion of blue balls given a dot:
- Calculation identical to standard Bayesian updating experiments
- But can also just count...
After gaining experience will ask WTP against standard counting task
Bayesian Updating
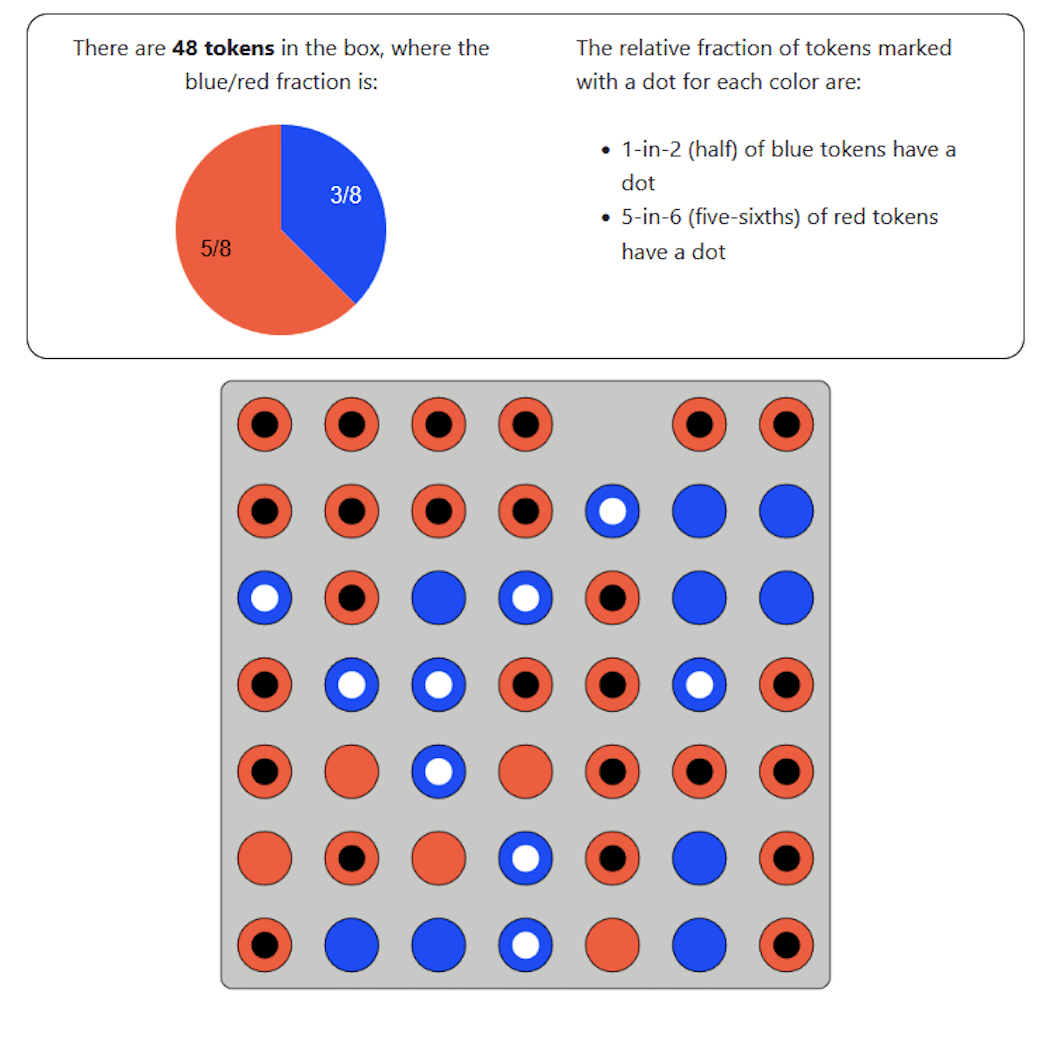
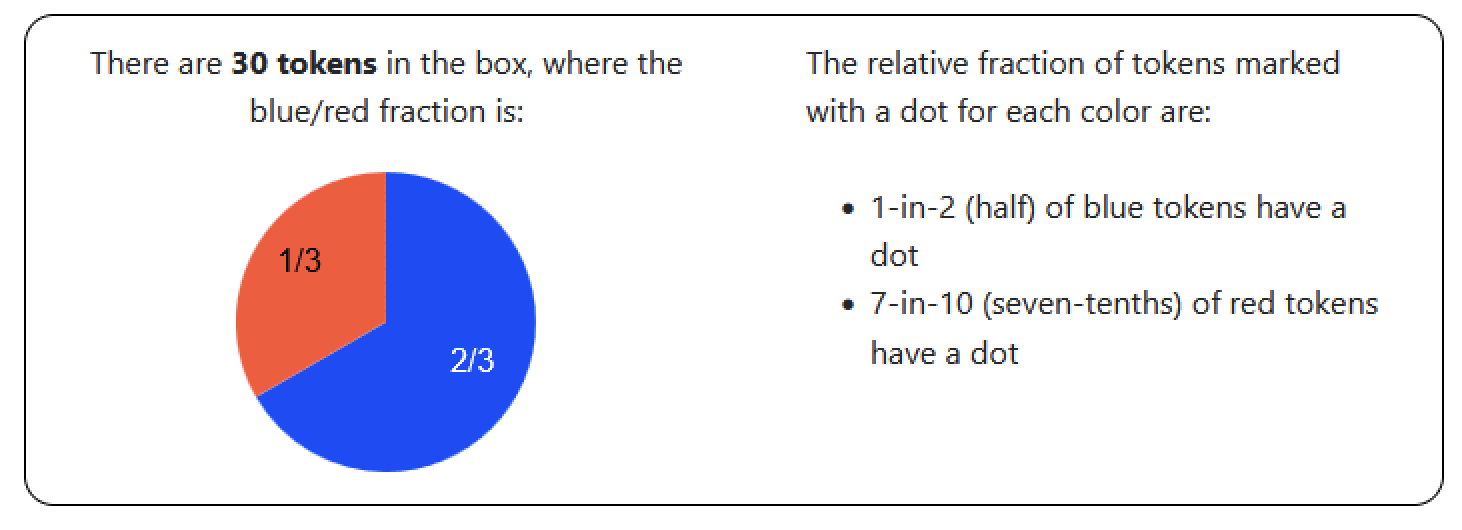
Calc or Count
Calc only
Proportion of Blue dotted tokens
Can they do it?

Bayesian Updating
Elicit how much they require to do the task:
Bayesian Updating: WTA
For those who can do the calculation


For those who can't
Avg: $0.82
Avg: $0.99
Conclusions (so far...)
- Close enough incentive works best well for inducing effort but requires binomial/cardinal realizations
- Varying the incentives:
- No substantive differences across BSR presentations
- Offering incentives and letting them choose effort is dominated by authority of telling them what to do
- For a Bayesian updating task:
- 50% or Prolific subjects can perform the calculation if given frequentist version
- Need to be given ~$0.55 to offset costs
CostlyBelief-BSF
By Alistair Wilson
CostlyBelief-BSF
- 76


