Transparent Randomization
A Field Study of the Champions League
Alistair Wilson
University of Pittsburgh
Marta Boczon
Copenhagen Business School
Main Idea
- Randomization a frequently used market design tool:
- Often used to ensure fair treatment
- Establishes fair treatment ex ante, where outcomes can still be very unfair
- But if the point of randomization is equity:
- not only does it need to actually be fair
- It also needs to be perceived/understood as fair
- But this can be hard in complicated mechanisms, or constrained assignments where outcomes are complex and inter-related
- How to have stakeholders understand their ex ante fair treatment!?
Solutions
Will outline a high-stakes randomized assignment with non-trivial constraints that has been broadly accepted by the general public with the following elements:
- Physically conducted draws
- All randomizations as simple uniform draws
- Dynamic procedure that assembles the assignment with comprehensible elements
- Separation between randomization and algorithm
- Algorithm: Deterministic (but very complex)
- Randomization: Simple draws from an urn
Most Public-Facing Randomizations are Constructed with Uniforms
Most Public-Facing Randomizations are Constructed with Uniforms
But examples make clear some design latitude:
- While component are discrete uniforms...
- ... distributions often non-trivial interactions
- ... both with/without replacement
UEFA Champions League Draw
- High stakes (millions of euro on the line)
- Huge public engagement (millions of viewers)
- Very complicated outcome:
- Matching of 8 teams to 8 teams
- Non-trivial matching constraints
- Teams that played together at prior stage
- Teams from the same country/association
Urn \(A\)
Urn \(B\)
Procedure
Urn \(A\)
Urn \(B\)
Round 1: Runner-up
Urn \(A\)
Urn \(B\)
Round 1: Runner-up
Excluded
Urn \(A\)
Urn \(B\)
Round 1: Winner
Excluded
Urn \(A\)
Urn \(B\)
Match made
Excluded
Urn \(A\)
Urn \(B\)
Round 2: Runner Up
Excluded
Urn \(A\)
Urn \(B\)
Round 2: Runner Up
Excluded
Urn \(A\)
Urn \(B\)
Round 2: Winner
Excluded
Urn \(A\)
Urn \(B\)
And so on...
Excluded
Dynamic Urn Draw
- Constraint set \(H\) implies set of feasible assignments \(\Gamma_H\)
- Direct constraint make sure that excluded team pairs aren't allowed to happen
- Dynamic constraints via a computer algorithm ensure that given the current state of the draw, all subsequent draws will not violate the constraints:
W(r,\mu )=\left\{w\in\mathcal{W} \left| \exists\left(\mu,\mu^{\prime} \right) \in \Gamma_H \text{ s.t. }(w,r)\in\mu^{\prime} \right.\right\}
Winners
Exists feasible assignment given current state \(\mu\)
\(r\) is valid partner
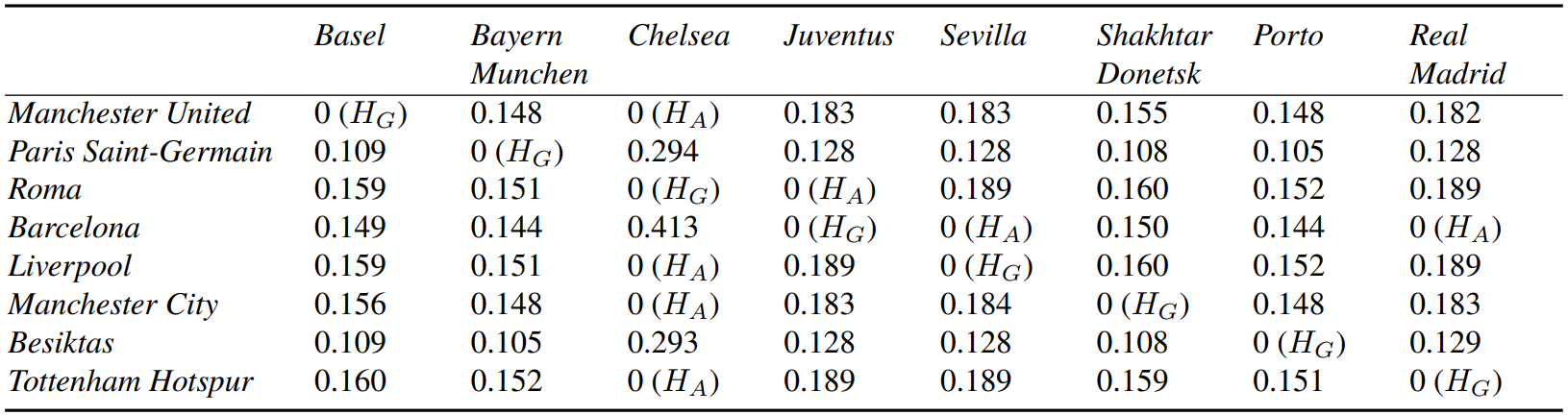
Resulting Match Probabilities
(2018 Draw)
- Can we quantify the distortions across otherwise equally treated teams?
- Can we construct a fairer randomization?
Distortions
Distortions
Distortions
- Largest beneficiary: Real Madrid in 2017
- Realization: Champions
- Worst hit: Arsenal in 2014
- Realization: eliminated in R16
Distortions
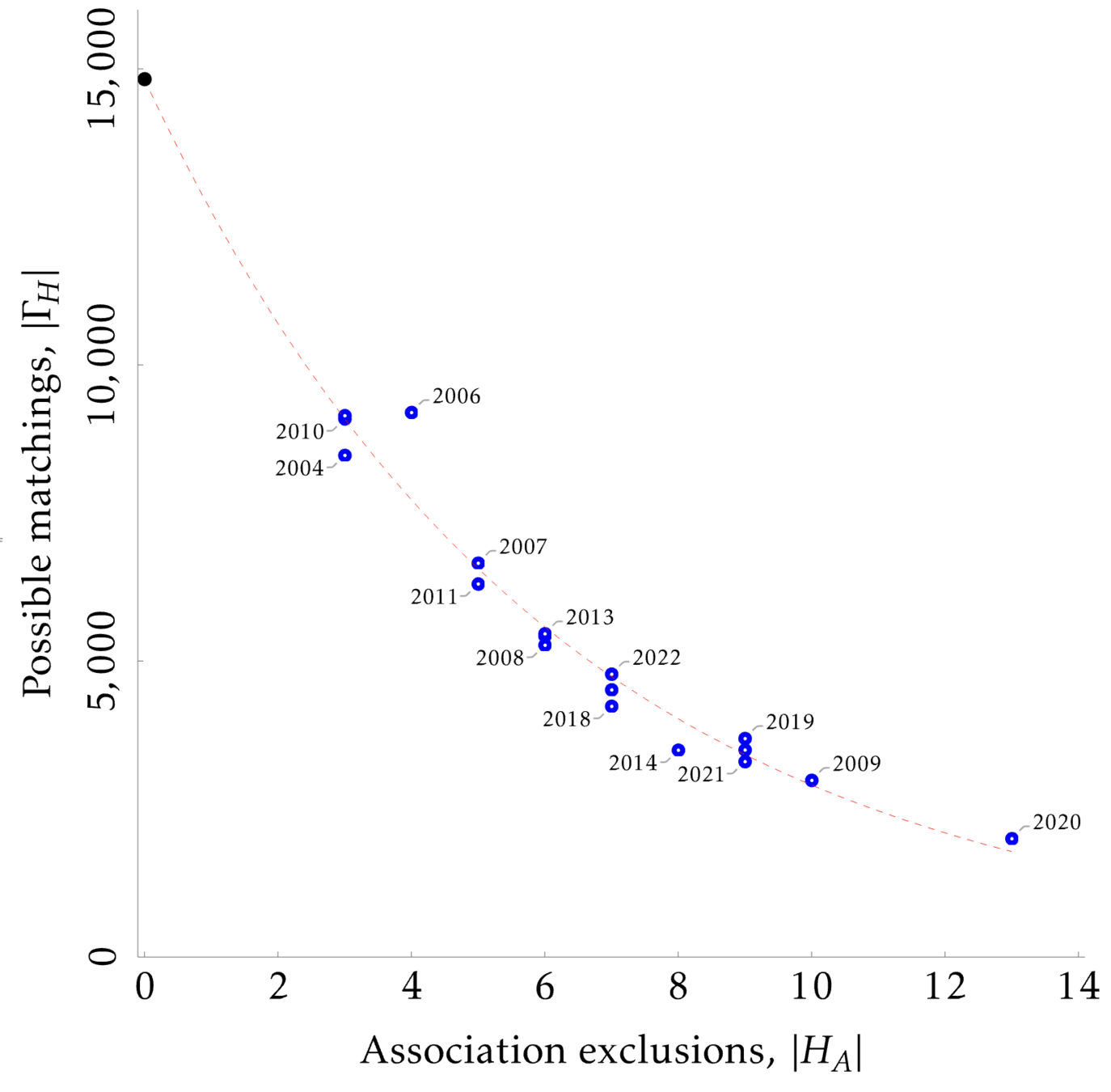
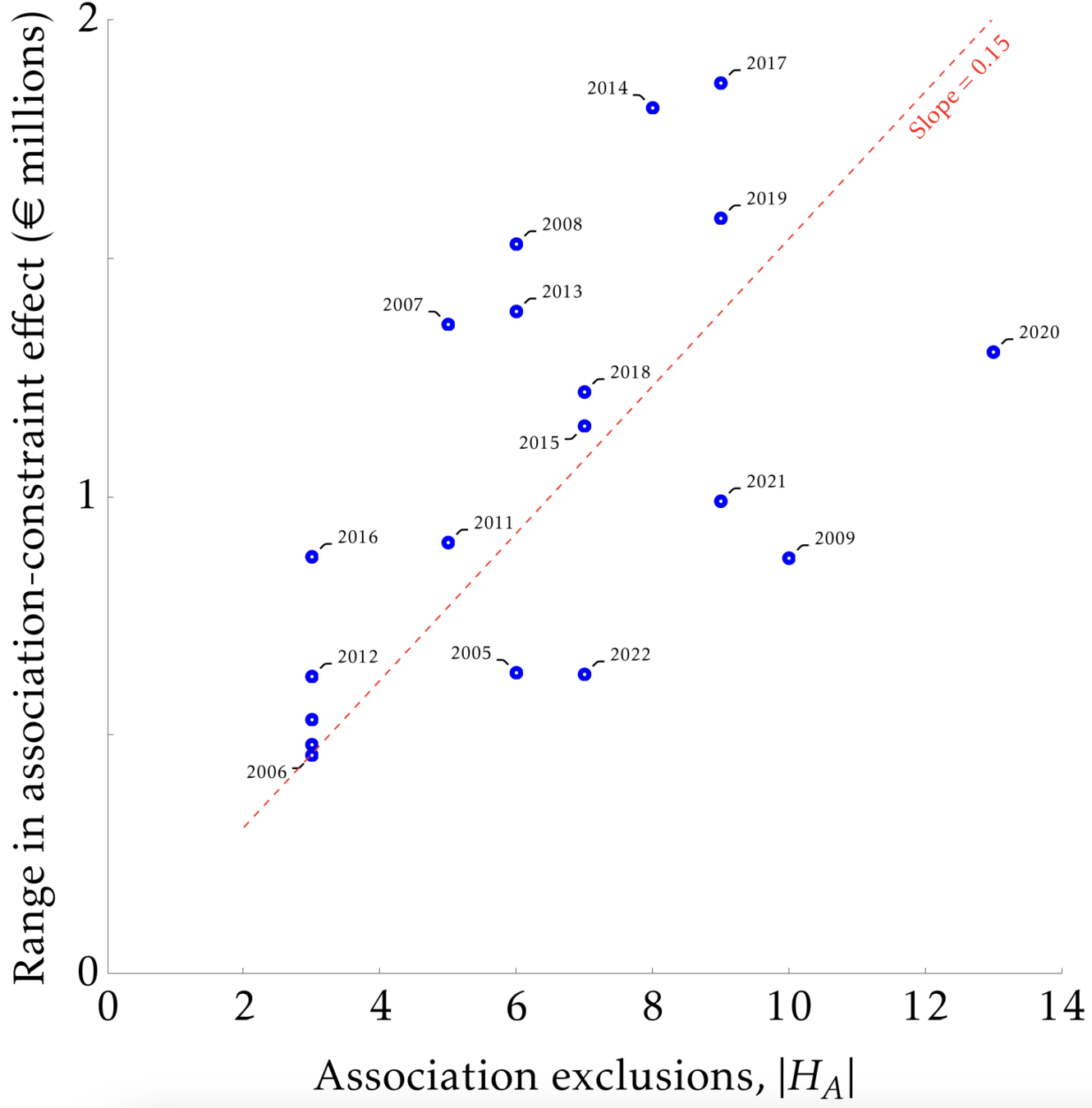
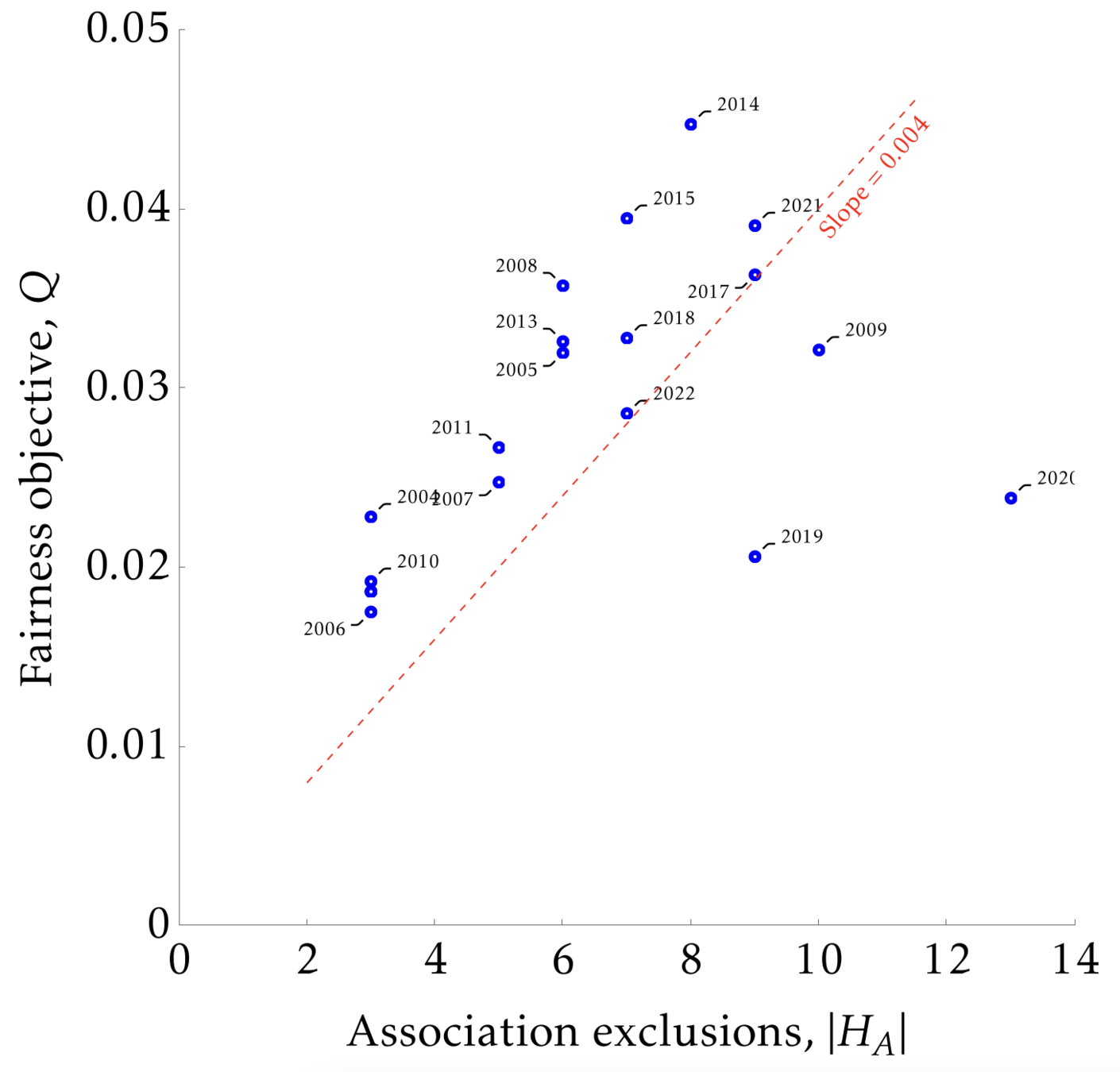
Want a simple metric for match-level distortions
- Consider two teams \(i\) and \(j\) that are not excluded from matching to a third team \(k\) via:
- \( \Delta P_{i,j,k} :=\left|P_{i,k} - P_{j,k}\right| \)
- Considering average distortion across all feasible \((i,j,k)\) comparisons \(Q(P) \)
If all equally treated teams have equal odds of matching, then this is minimized at \(Q=0\)
Distortions
Are Fairer designs Possible?
- The UEFA design is centered around transparency to outside observers.
- Question: Does transparency come at a fairness cost, increasing the distortions?
- Answer possible due to Market Design tool:
Are Fairer designs Possible?
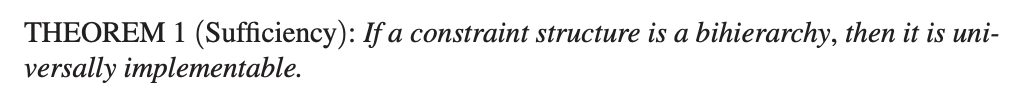
A biheirarchy here means the constraints can be divided into two groups of constraints with subset ordering
Match exclusions
Row team has exactly 1 partner
Column team has exactly 1 partner
Heirachy \(\mathcal{H}_1\)
Heirachy \(\mathcal{H}_2\)
\(\Rightarrow\) Any expected assignment matrix satisfying the constraints is implementable as a lottery over \(\Gamma\)
Any expected assignment matrix satisfying the constraints is implementable as a lottery over \(\Gamma\)
But this means we can choose an expected assignment matrix \(\mathbf{P}\) (that satisfies the constraints) to maximize:
Q(P)=\frac{1}{\left| \Upsilon \right|} \sum_{(i,j,k)\in \Upsilon}\left|P _{i,k}-P _{j,k}\right|
Reduce the dimensionality of the problem from ~6000 degrees of freedom to ~50 !
- Optimal fairness design can increase equality of outcomes by ~10%
- But this must be set against reduced transparency
- optimal constructions will be a black box
To all extents and purposes, the conclusion is that given the constraints, the UEFA procedure is essentially fair!
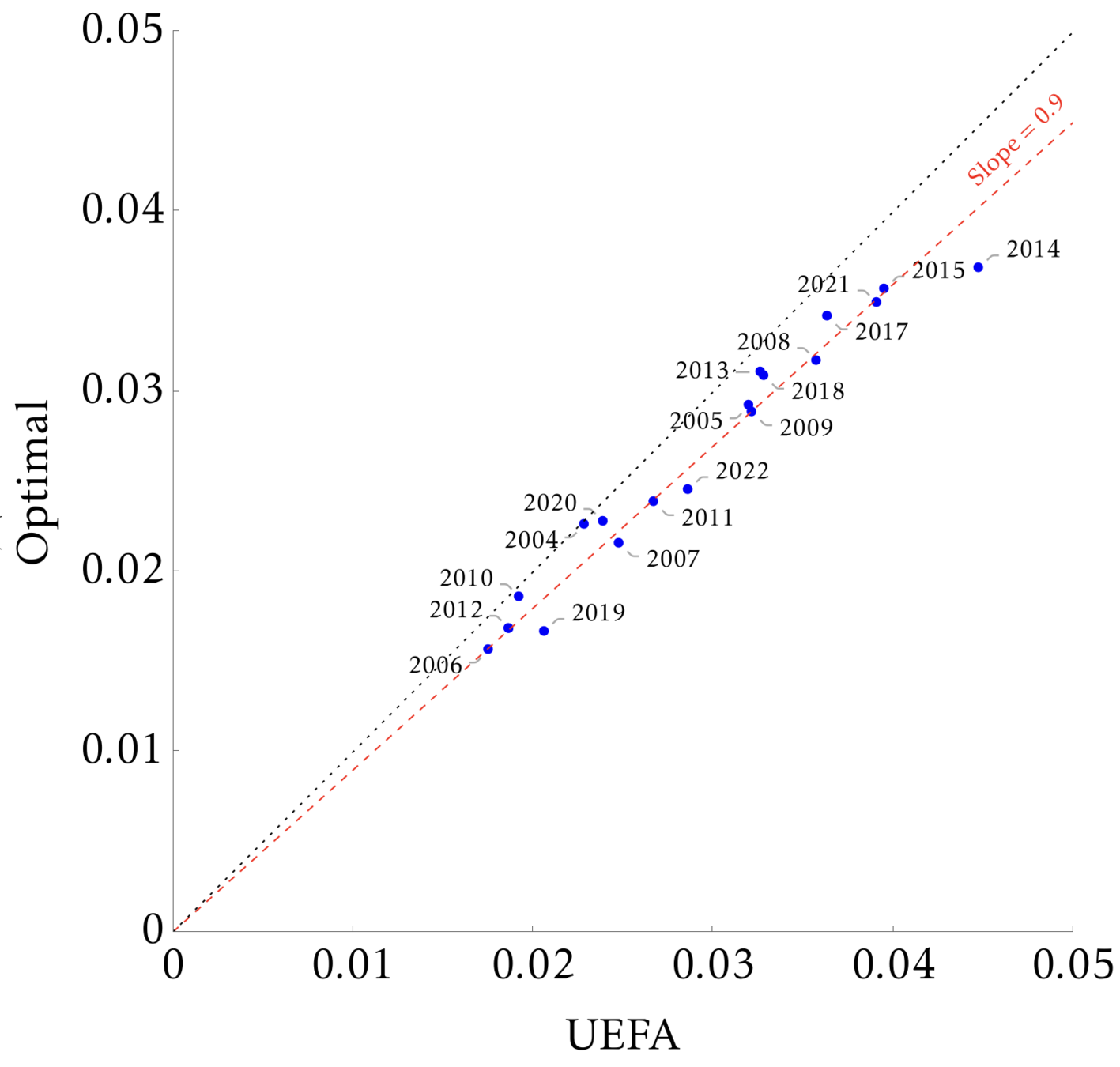
Weakening the Constraints
While the mechanism is close to optimal given the constraints, we can employ similar analyses to understand the fairness gains from weakening the constraints.
\rightarrow \left\{\mu \in \mathcal{A}\Bigl| \left| \mu \cap H\right|\leq 1 \bigr.\right\}
\Gamma_H := \left\{\mu \in \mathcal{A}\Bigl| \left| \mu \cap H\right| = 0 \bigr.\right\}
So the weakened constraints allows for at most one of the excluded matches, where the other is complete proscription
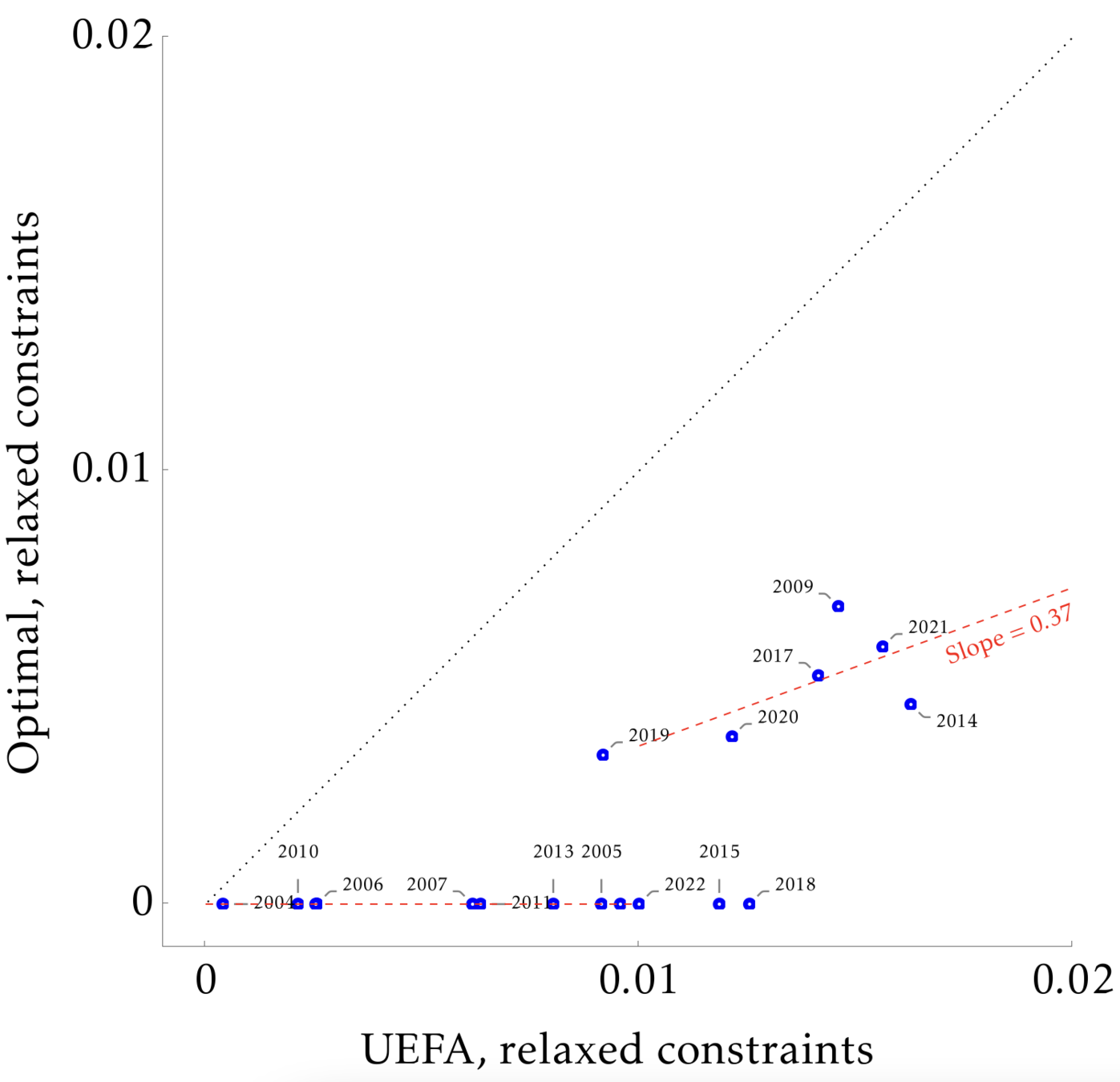
Relaxed constraint Set
Generalization Example
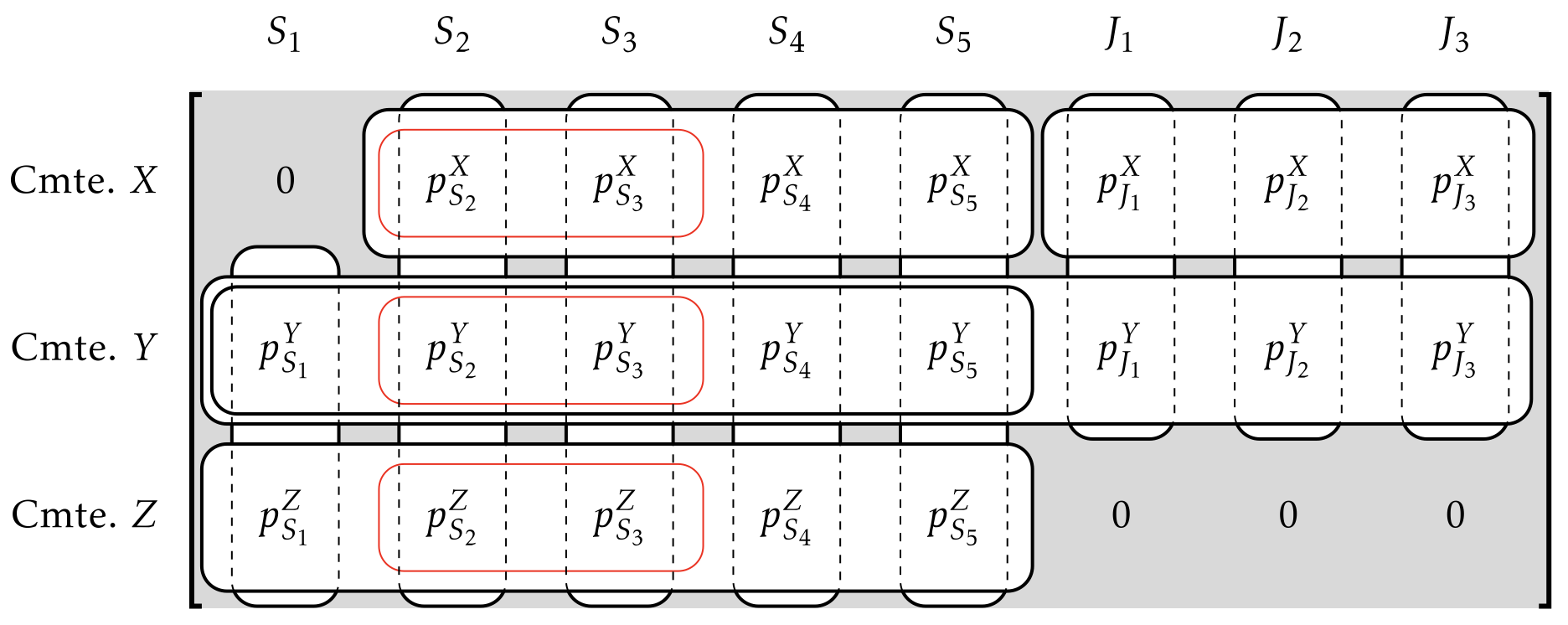
Filling three committees:
- CMTE X: 2 Seniors and 1 Junior
- CMTE Y: At least 1 senior, 3 total
- CMTE Z: 3 Seniors
People:
- Seniors at most 2
- Juniors at most 1
- \(S_2\) and \(S_3\) can't serve together
- Chair can't serve on \(X\)
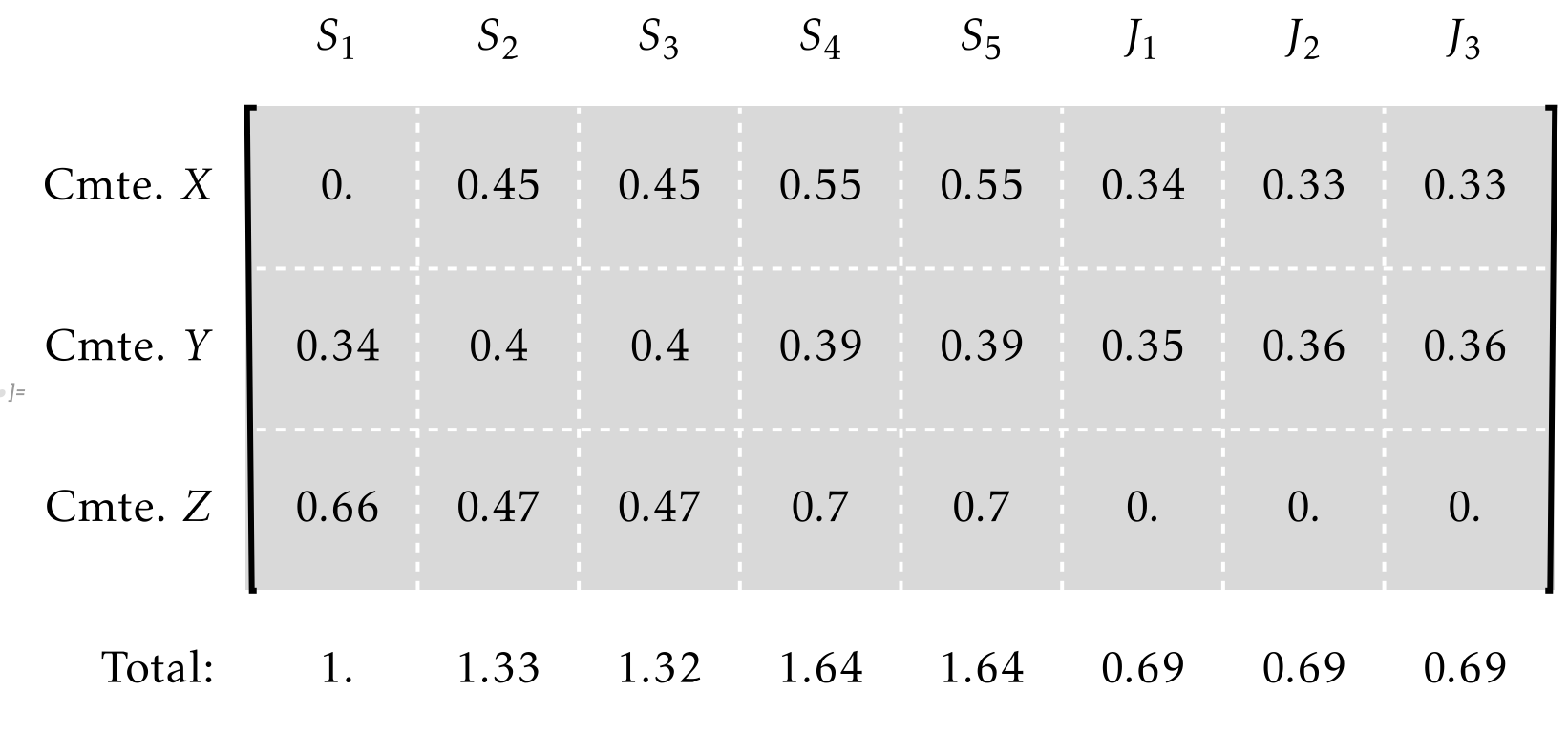
- One-to-one matching exhibits near optimality
- Not the case in many-to-many (here demonstrated by counter-example) as expected assignment here has a great deal of inequality in usage
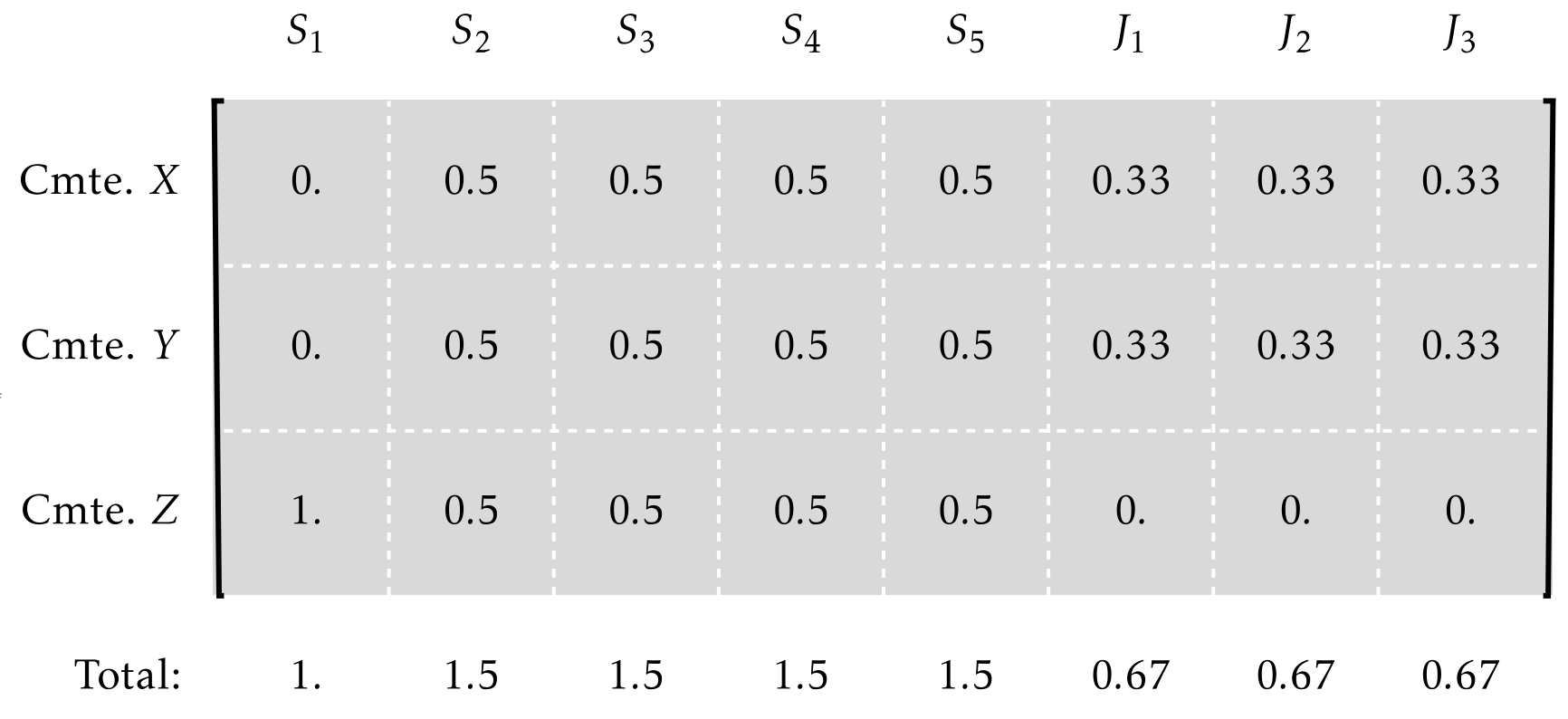
- The following expected assignment is feasible (and implementable as are biheirarchy)
- However, can be implemented by the simple dynamic draw:
- Need to add further constraints!
Conclusions
- Document a transparent randomization, designed to solve a complex combinatoric assignment
- Organization developed a solution under a behavioral constraints that would not initially be obvious to economists
- However, economists do have a great set of tools that can aid with understanding and assessing the design
- Moreover, through these tools, we can find the generalizations that can extend to other settings
Make Sure to Bring a Coat
TransparentRandomization
By Alistair Wilson
