Dynamical instabilities and the Onset of Chaos in Tight Planetary Systems
Almog Yalinewich - 26.12.19
Preamble
The Two Body Problem
\frac{d A}{d t} \approx r^2 \dot{\theta} \approx l
Kepler's second law
\frac{d v}{d \theta} \approx \frac{d v}{d t} / \frac{d \theta}{d t} \approx \frac{G M}{r^2} / \frac{l}{r^2} \approx \frac{G M}{l}
In velocity space, the particle always moves on a circle
\vec{v} = \vec{v}_0 + \frac{G M}{l} \hat{\theta}
Cross with angular momentum and get the conserved LRL vector
\vec{A} = \vec{l} \times \vec{v}_0 =\vec{l}\times \vec{v} - G M \hat{r}
always points toward the periapse
Types of Structure Formation
Monolithic
Polylithic
Planetary Collisions
- Composition
- Atmospheric Mass
- Spin
- Orbital Parameters
Collision Course
\approx 1 M_{☽}
M_i \approx \frac{\left(\Sigma a^2\right)^{3/2}}{M_s^{1/2}}
Isolation mass
How long?
Teetering on the Verge of Stability
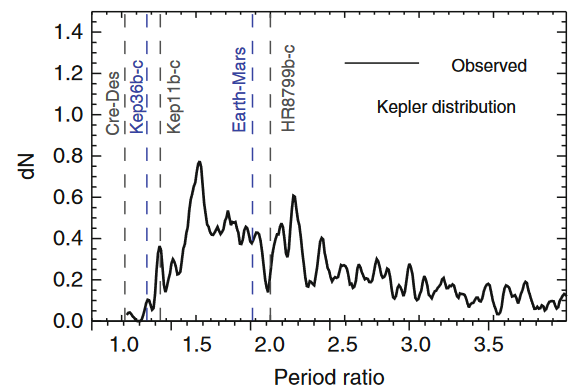
Dawson 2018
High Energy Connection
Every Gyr per solar system =>
1 per week in the galaxy
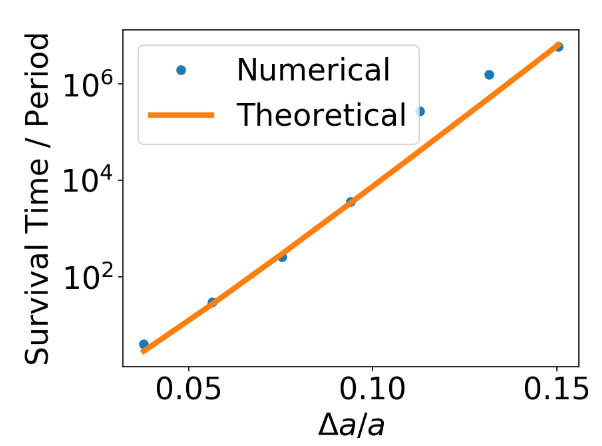
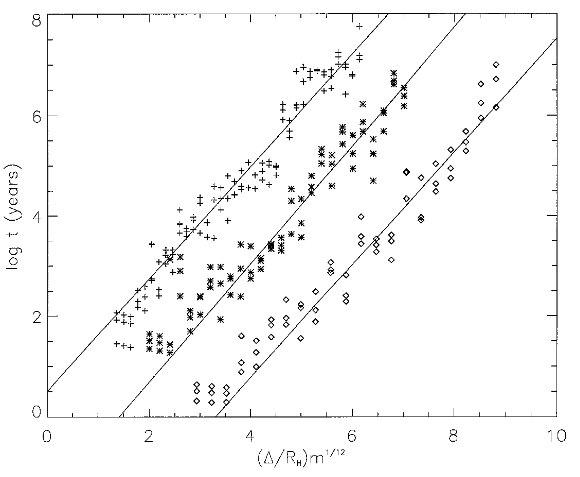
Survival Time of Tight Co-planar Planetary Systems
M
m
a
\Delta a
T = \sqrt{\frac{a^3}{G M}} f \left(\frac{\Delta a}{a}, \frac{m}{M}\right)
m \ll M, \, \Delta a \ll a
Numerical Experiments
\log \left(\rm yr\right)
\Delta \propto \Delta a /a
Rice et al. 2018
Previous Paradigm -
Chaotic Diffusion
m
\delta v_{\perp} \approx \frac{G m}{b v}
b
\delta v_{\perp}
v
Impulse Approximation
\delta v_{\theta} \approx e \frac{G m}{\Delta a^2} \sqrt{\frac{a^3}{G M}}
\delta v_{\perp} \approx \frac{G m}{\Delta a^2} \sqrt{\frac{a^3}{G M}}
v \approx \sqrt{\frac{G M}{a}} \frac{\Delta a}{a}
\delta v_{\perp} \approx \frac{G m}{b v}
a
\Delta a
\sqrt{\frac{G M}{a}} \frac{\Delta a}{a}
Planet - Planet Scattering
T \propto \left(\Delta a/a\right)^8
Higher order interaction gives
Not steep enough
T \approx t_s \left(\frac{e_f}{\delta e}\right)^2 \approx \sqrt{\frac{a^3}{G M}} \left(\frac{\Delta a}{a}\right)^5 \left(\frac{M}{m}\right)^2
e_f \approx \frac{\Delta a}{a}
\delta e^2 \approx \frac{\delta j}{j} \approx \delta v_{\theta} / \sqrt{\frac{G M}{a}} \Rightarrow \delta e \approx \frac{m}{M} \frac{a^2}{\Delta a^2}
t_s \approx \sqrt{\frac{a^3}{G M}} \frac{a}{\Delta a}
Diffusion Time
Evolution of Orbital Parameters
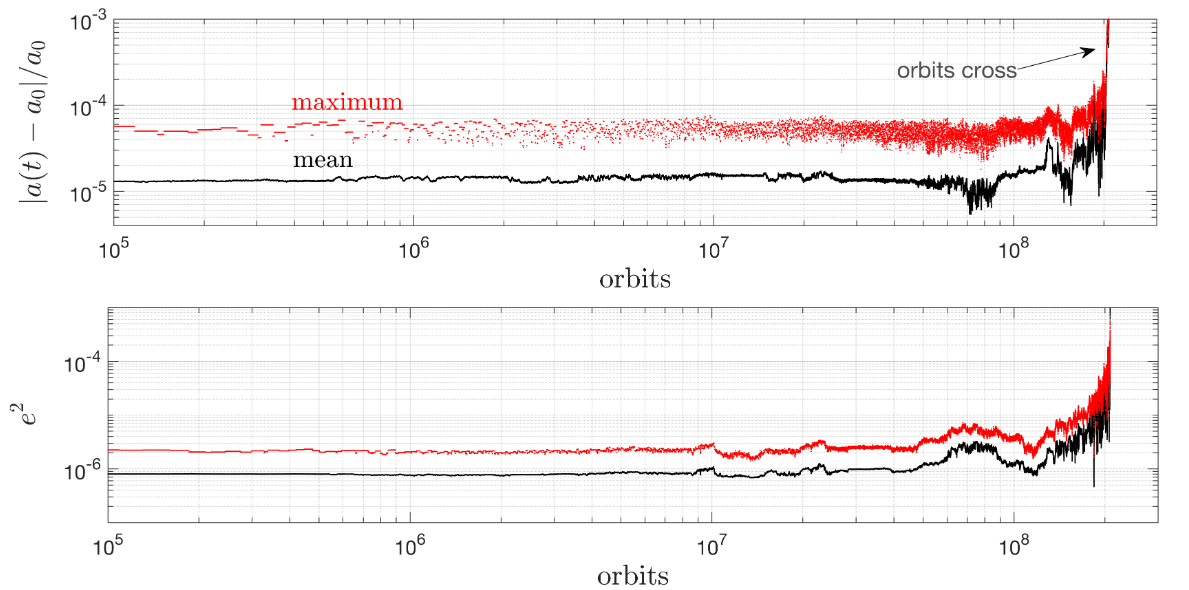
Diffusion predicts gradual increase
Evolution of Orbital Parameters
\psi \approx \pm \frac{m}{M} \frac{a^2}{\Delta a^2}
\psi
\vec{e} = \frac{\vec{v} \times \vec{j}}{G M} - \hat{r}
Energy / Angular momentum unchanged, but the position of periapse does change
\delta v_{r} \approx \frac{G m}{\Delta a^2} \sqrt{\frac{a^3}{G M}}
Periapse Drift
Failure of Chaotic Diffusion
Ellipse anti - alignment
Angles are not random
Theoretical explanation for survival time steepness?
KAM Theory
Hamiltonian Perturbation Theory
H = H_0 \left( \vec{I}\right) + \varepsilon H_1 \left(\vec{I}, \vec{\varphi} \right)
\varepsilon = 0 \Rightarrow \vec{I} = {\rm const}, \vec{\varphi} = \vec{\varphi}_0 + \vec{\omega} t, \vec{\omega} = \nabla_{I} H_0
KAM result: for a sufficiently small
\varepsilon
the deviation is bounded forever
\left|\vec{I} \left(t\right) - \vec{I} \left(0\right)\right| < C
Original Proof
H = H_0 \left( \vec{I}\right) + \varepsilon H_1 \left(\vec{I}, \vec{\varphi} \right)
Try to find a canonical change of variable
\vec{I}'\left(\vec{I}, \vec{\varphi}, \varepsilon\right), \vec{\varphi}' \left(\vec{I}, \vec{\varphi}, \varepsilon \right)
Such that the new Hamiltonian is
H' = H_0' \left( \vec{I}'\right)
Solution by iterations => convergence for finite
\varepsilon
Why doesn't this always work?
Periodic Points
Coordinates are just labels. Nothing special about them
What would prevent you from re - labeling the perturbed trajectory to the unperturbed trajectory?
Mapping preserves periodic points
If the perturbed trajectory has periodic points, it cannot be mapped to the unperturbed trajectory
System with Two Degrees of Freedom
I_1, \varphi_1
I_2, \varphi_2
\frac{\omega_2}{\omega_1} = \frac{\partial H/\partial I_2}{\partial H/\partial I_2} \notin \mathbb{Q}
No fixed points
System with Two Degrees of Freedom
I_1, \varphi_1
I_2, \varphi_2
Complete circle
\rho \notin \mathbb{Q}
Treasure Hunt Model
I, \varphi
\varphi_0
\varphi_1
\varphi_{n+1} = \varphi_n + \rho+\eta \left(\varphi_n\right)
Creating Fixed Points
\rho \ll 1 \Rightarrow \rho < \left| \eta \left(\varphi\right) \right|
\left|\frac{1}{2} - \rho \right| \ll 1 \Rightarrow \left|\frac{1}{2} - \rho\right| < \left| \eta\left(\varphi\right) + \eta \left(\varphi + \frac{1}{2} \right) \right|
Every irrational number can be approximated by a rational number
Dirichlet's Theorem
\left|\alpha - \frac{p}{q} \right| < \frac{C}{Q^{\nu}}
p \in \mathbb{Q}
0 < q \le Q \in \mathbb{Z}
\alpha \notin \mathbb{Q}
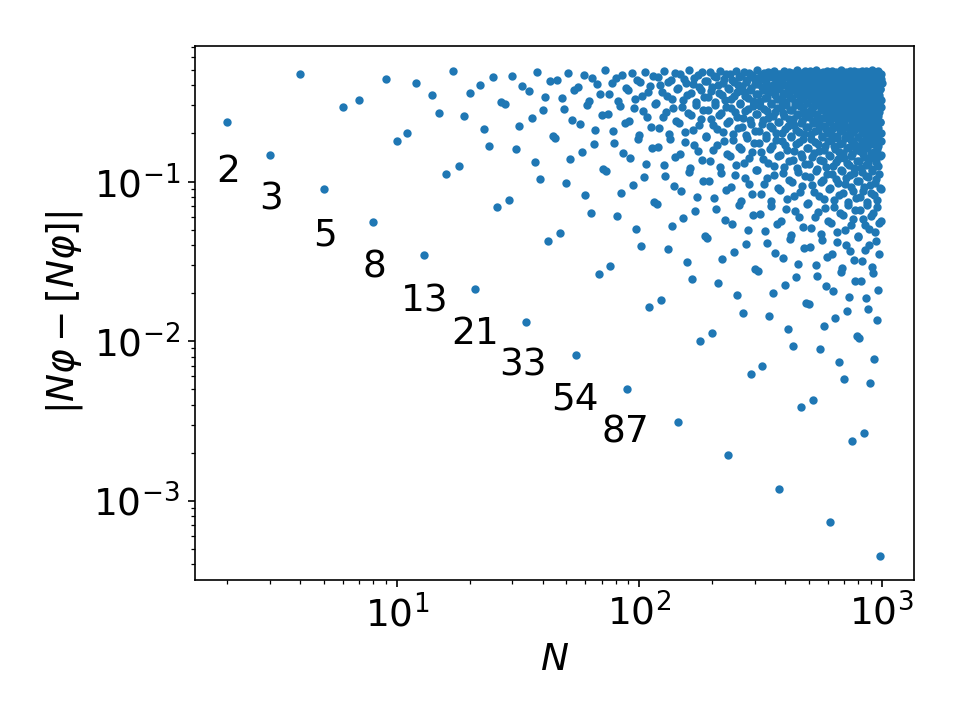
Multiple Steps
\varphi_n \approx \varphi_0 + n \rho + \eta_N \left(\varphi_0\right)
\eta_n\left(\varphi_0\right) = \sum_{m=0}^{n-1} \eta \left(\varphi_0 + m \rho\right)
n \rho
declines polynomially (Dirichlet)
What about the perturbation ?
\eta_n\left(\varphi_0\right)
Fourier Transform
\eta \left(\varphi\right) = \sum_{l \neq 0} \hat{\eta} \left(l\right) \exp \left(2 \pi i l \varphi\right)
\eta_n \left(\varphi\right) = \sum_{l \neq 0} \hat{\eta} \left(l\right) \exp \left(2 \pi i l \varphi\right) \frac{1 - \exp \left(2 \pi i nl \rho\right)}{1- \exp \left(2 \pi i l \rho\right)}
This sum looks complicated, but it is actually dominated by a single term
Asymptotics
\eta_n \left(\varphi\right) = \sum_{l \neq 0} \hat{\eta} \left(l\right) \exp \left(2 \pi i l \varphi\right) \frac{1 - \exp \left(2 \pi i nl \rho\right)}{1- \exp \left(2 \pi i l \rho\right)}
Critical value
1 - \exp \left(2 \pi i n l \rho \right) \approx 2 \pi in C l^{-\nu} \approx 1
l_c \approx \left(2 \pi i n C\right)^{1/\nu}
l \ll l_c
l \gg l_c
\frac{1 - \exp \left(2 \pi i nl \rho\right)}{1- \exp \left(2 \pi i l \rho\right)} \approx \frac{l^{\nu}}{2 \pi iC}
\frac{1 - \exp \left(2 \pi i nl \rho\right)}{1- \exp \left(2 \pi i l \rho\right)} \approx n
\hat{\eta} \left(l\right) < \hat{\eta}_0 e^{-\sigma l}
Bound on Perturbations
\left|\eta_n \left(\varphi\right) \right| < \hat{\eta}_0 n \exp \left(- \sigma \left(C n\right)^{1/\nu}\right)
Attains maximum for some finite
n = n_s
No fixed points / system is stable if
\hat{\eta}_0 n_s \exp \left(- \sigma \left(C n_s\right)^{1/\nu}\right) < C n_s^{-\nu}
\left|\eta_{n_s} \left(\varphi\right) \right| < n_s \rho
Nekhoroshev Estimates
Opposite extreme: very unstable conditions
\hat{\eta}_0 n \exp \left(- \sigma \left(C n\right)^{1/\nu}\right) > C n^{-\nu}
Hence
\hat{\eta}_0 n > C n^{-\nu} \Rightarrow \left(C/\hat{\eta}_0\right)^{1/\left(\nu+1\right)}
n > \left(\frac{C}{\hat{\eta}_0}\right)^{\frac{1}{\nu+1}} \exp \left(\frac{\sigma}{\nu +1} \frac{C^{\frac{2 \nu}{\nu^2+\nu}}}{\hat{\eta}_0^{\frac{1}{\nu+1}}}\right)
Substituting back to the exponent
Exponential dependence on the strength of the perturbation
Nekhoroshev Estimates in Hamiltonian Systems
H \left(\vec{I}, \vec{\varphi}\right) = H_0 \left(\vec{I}\right) + \varepsilon H_1 \left(\vec{I}, \vec{\varphi}\right)
Actions are bounded for exponentially long time
\left|\vec{I} \left(t\right) - \vec{I} \left(0\right)\right| < C_1 \varepsilon^{\frac{1}{2 \mathcal{N}}}
t < T = C_2 \exp \left(C_3/\varepsilon^{1/2 \mathcal{N}}\right)
\mathcal{N} - {\rm \# \, of \, degrees\, of\, freedom}
Nekhoroshev Estimates for Tight Planetary Systems
Dependence on Separation
\phi \propto \frac{1}{\sqrt{r_1^2+r_2^2 - 2 r_1 r_2 \cos \gamma}} \propto \sum_j b^j_{1/2} \left(\frac{r_2}{r_1}\right) \cos \left(j \gamma\right)
Interaction between planets
Fourier transform - Laplace coefficients
b_{1/2}^j \left(\alpha\right) = \frac{1}{\pi} \int_0^{2 \pi} \frac{\cos \left(j \theta \right) d \theta}{\sqrt{1+\alpha^2 -2 \alpha \cos \theta}}
Asymptotic expansion
b_{1/2}^j \left(\alpha\right) \propto \exp \left(- \left(\alpha - 1\right) \left|j \right|\right)
\ln T \propto \Delta a/a
Dependence on Mass
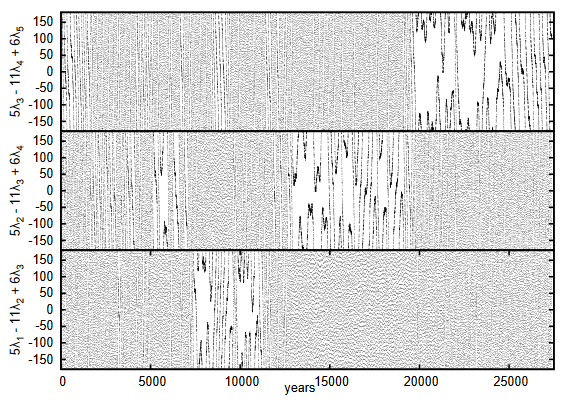
Quillen 2011 argues for three body resonance overlap
Three body resonant Hamiltonian independent of periapse direction
6 DOF
Two conserved quantities (Energy & Angular momentum)
12 DOF
4 DOF
Small parameter
m^2/M^2
\log T \propto \sqrt[4]{m/M}
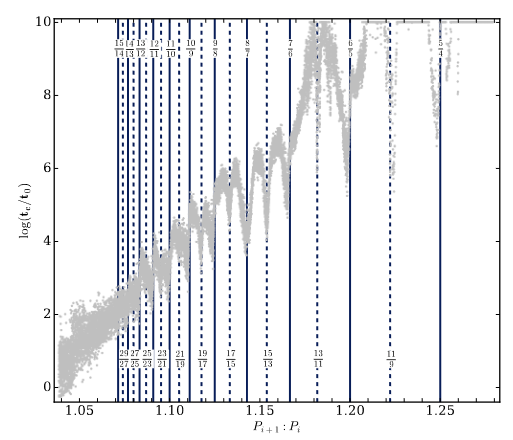
Laplace Resonance
\lambda_1 p_1+\lambda_2 p_2 + \lambda_3 p_3 = 0
\lambda = t \sqrt{G M/a^3}
p_1, p_2, p_3 \in \mathbb{Z}
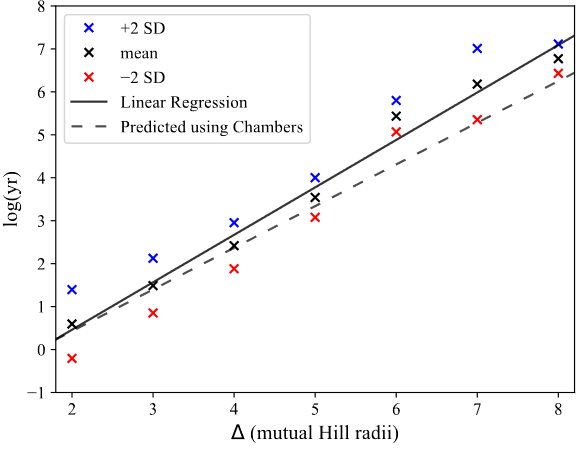
Ansatz for The Survival Time
T \approx c_1 \sqrt{\frac{a^3}{G M}} \frac{a}{\Delta a} \exp \left(c_2 \frac{\Delta a}{a} \frac{m^{1/4}}{M^{1/4}}\right)
Yalinewich & Petrovich 2019
c_1 = 4 \cdot 10^{-5}, \, c_2 = 8
Packing Metric
Previous paradigm:
T = f \left(\Delta \right)
Hill Parameter
\Delta \approx \frac{\Delta a}{a} \left(\frac{M}{m}\right)^{1/3}
We predict
T \approx f \left(\frac{\Delta a}{a} \left(\frac{M}{m}\right)^{1/4}\right)
Actually fits better to simulations
Packing Metric
Chambers et al. 1996
Two Body Resonances
Obertas et al 2017
Conclusion
Theoretical model for the survival time of tightly packed, co - planar, non resonant planetary systems
Future directions: effects of inclination & resonance
Questions?
Paradigm shift:
- Chaotic diffusion
- Packing metric
stability of planetary systems
By almog yalinewich
