THE HOT JUPITER PERIOD-MASS DISTRIBUTION AS A SIGNATURE OF IN SITU FORMATION
Desert in sma-mass space
?
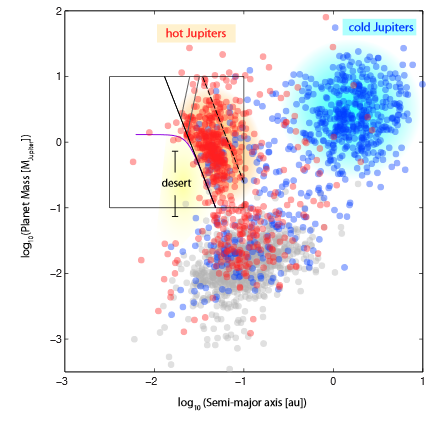
Magnetic Disc Truncation
B
Star
Disc
Competition between ram and magnetic pressures
v_r
Ram pressure
Disc
v_r
v_r \propto v_k \propto \sqrt{\frac{G M}{a}}
\rho \approx \frac{\dot{M}}{a^2 v_r}
P_{\rm ram} \approx \rho v_r^2
Magnetic Pressure
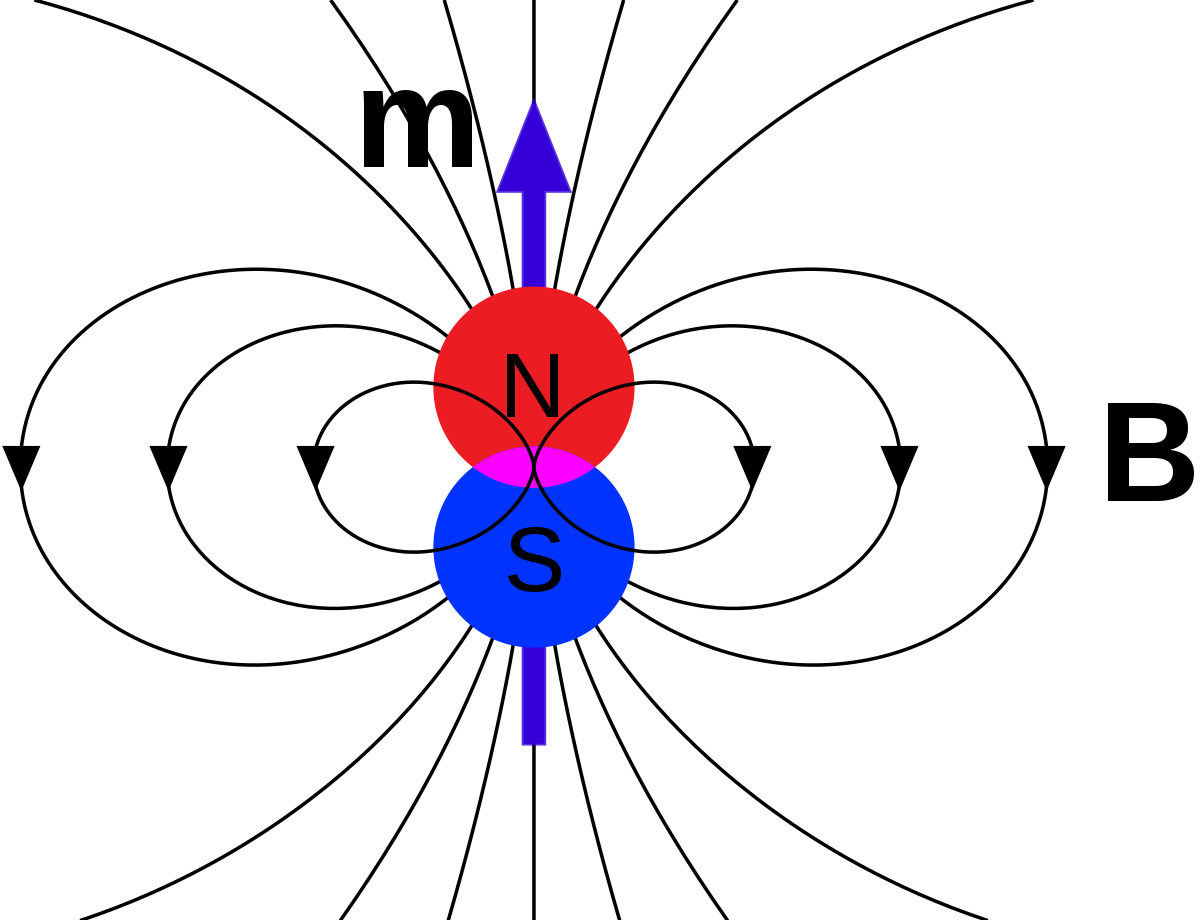
B \approx \frac{\mu}{a^3}
P_{\rm mag} \approx B^2
P_{\rm mag} \approx P_{\rm ram} \, \Rightarrow \, a \propto \dot{M}^{-2/7}
m \propto \dot{M} \, \Rightarrow \, a \propto m^{-2/7}
Tidal Torque - the easy bit
x
a
m
M
R
Tidal Torque - the easy bit
\frac{G M}{R^2} x \approx \frac{G m}{a^3} R^2 \Rightarrow \frac{x}{R} \approx \frac{m}{M} \left(\frac{R}{a}\right)^{3}
\Delta M \approx \frac{M}{R^3} R^2 x \Rightarrow \Delta M \approx m\left(\frac{R}{a}\right)^{3}
T \approx \frac{G m}{a^3} \cdot R\cdot R\cdot \Delta M\approx \frac{G m^2 R^5}{a^6}
n \frac{L}{T} \approx \sqrt{\frac{G M}{a^3}} m \sqrt{G M a}/T\approx \frac{M}{m} \left(\frac{a}{R}\right)^{5}
Hard bit - 6 orders of magnitude from Q
Holistic View
magnetic truncation
tidal torques
dynamical migration?
hot jupiter period-mass distribution
By almog yalinewich
