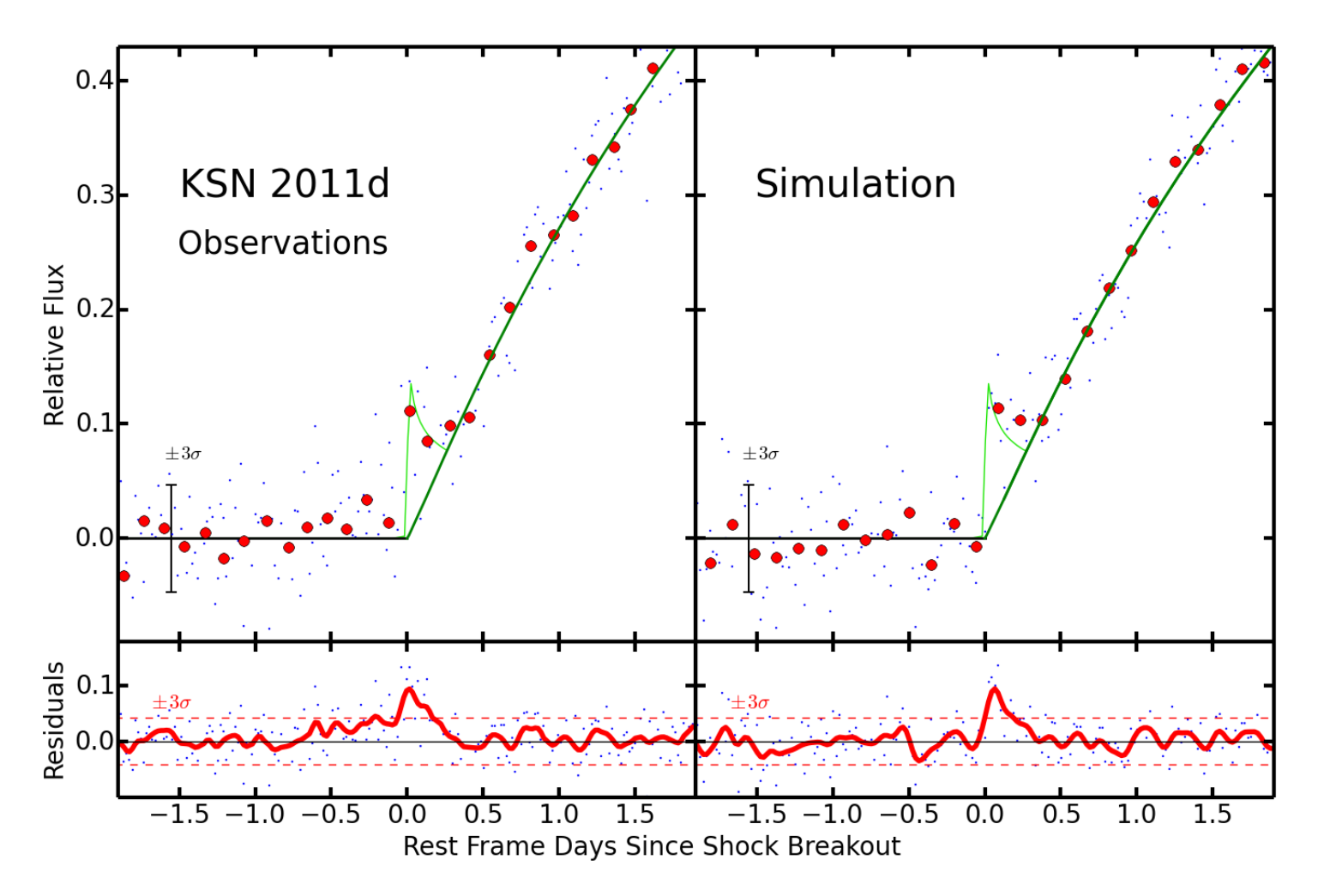
EARLY SUPERNOVA EMISSION - LOGARITHMIC CORRECTIONS TO THE PLANAR PHASE
Almog Yalinewich
Norm's Group Meeting
5.9.19
Hunt for the Progenitor
?
?
?
Forensics
Prompt
Breakout
Stellar Swan Song
Enter LSST
Physical Model
Explosion Mechanism
Shock Ascent
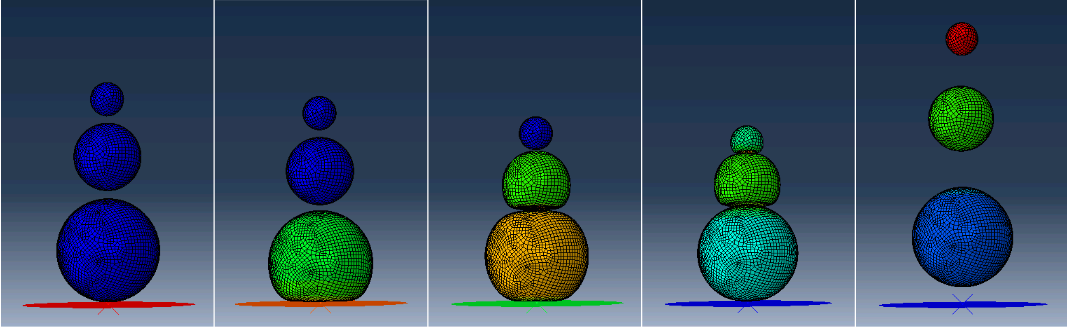
Distance from edge
Density
Velocity
Radiation Leak
x \approx D/v, \, D\approx \lambda c\Rightarrow \tau \approx c/v
Radiative Processes
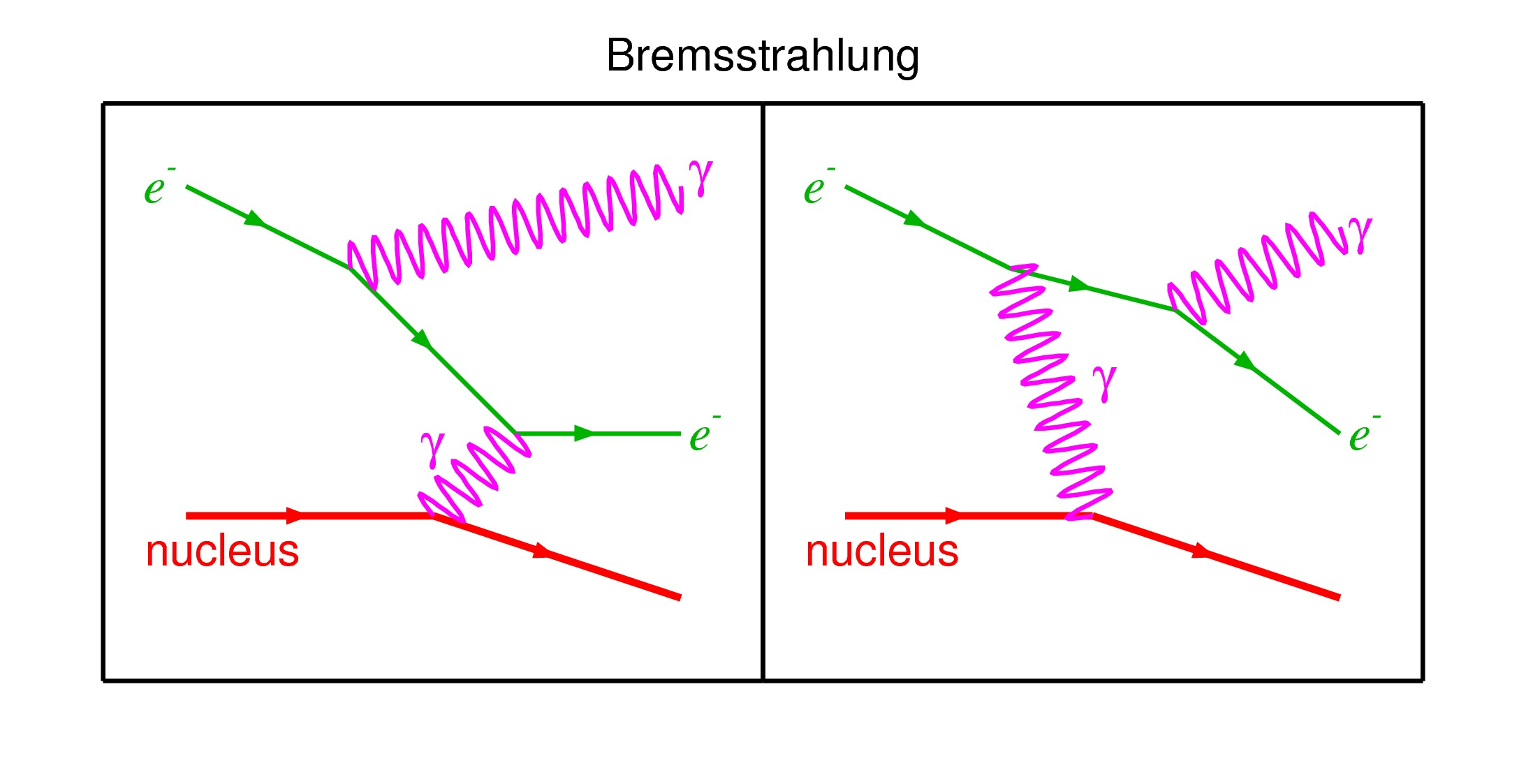
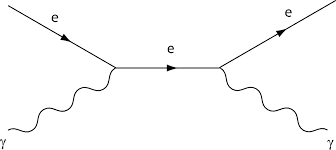
Why photons come
Why they stay
\sigma \approx r_e^2
\dot{n}_{bs} \approx \frac{\alpha c}{r_e^4} \left(n_b r_e^3\right)^2 \sqrt{\frac{m_e c^2}{k T}}
Shock Temperature
k T_m \approx m_p v^2
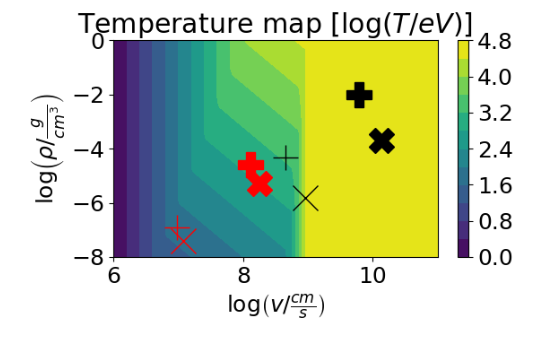
\rho v^2 \approx a T_r^4
k T_r \approx \rho^{1/4} v^{1/2} c^{3/4} h^{3/4}
k T_p \approx m_e c^2
k T_s \approx m_e c^2 \left(\frac{m_p}{\alpha m_e}\right)^2 \left(\frac{v}{c}\right)^8
Homologous Expansion
v \approx \frac{r}{t}
Planar Expansion
t
x
Same shell
Luminosity
Watching the same shell cool
V \propto t \Rightarrow U \propto t^{-1/3} \Rightarrow L \propto t^{-4/3}
Energy Problem
Energy would run out after one diffusion time
We have to go deeper!
Today's Paper
Diffusion in an Expanding Medium
\frac{\partial u}{\partial t} = \frac{\partial}{\partial x} \left(D \frac{\partial u}{\partial x}\right)
D \approx \lambda c \approx \frac{1}{\kappa \rho}
dm = \rho dx \propto d \tau
\frac{d x}{d t} = \frac{x}{t} \Rightarrow \rho \approx m^{\zeta} t^{-1}
\frac{\partial u}{\partial t} \approx \rho \frac{\partial^2u}{\partial m^2} \approx \frac{m^{\zeta}}{t} \frac{\partial^2 u}{\partial m^2}
\tau \propto m \propto \left(\ln t\right)^{\frac{1}{2-\zeta}}
Effect on Luminosity
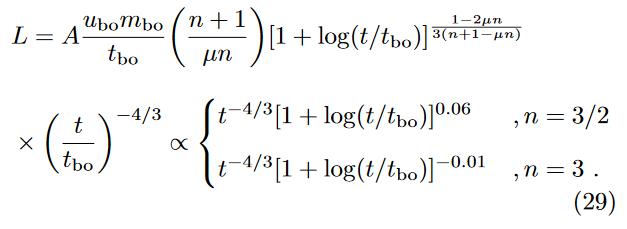
Effect on Temperature
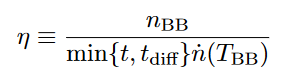
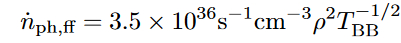
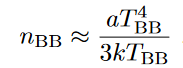
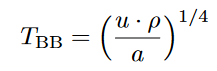
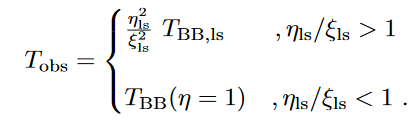
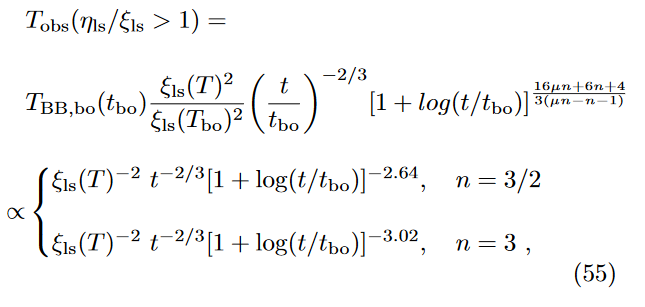
Progenitor Models
Red Supergiant
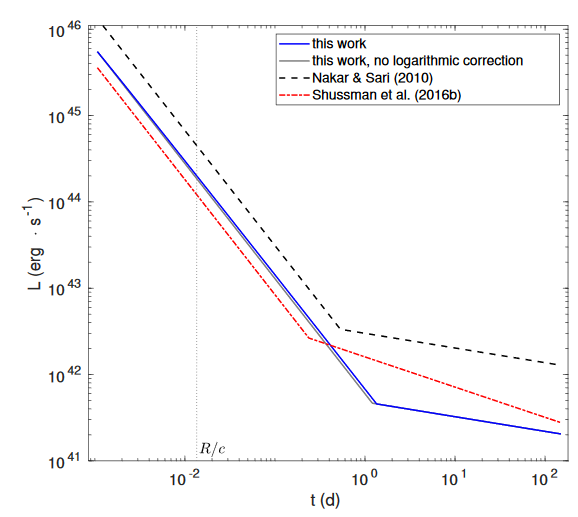
Red Supergiant
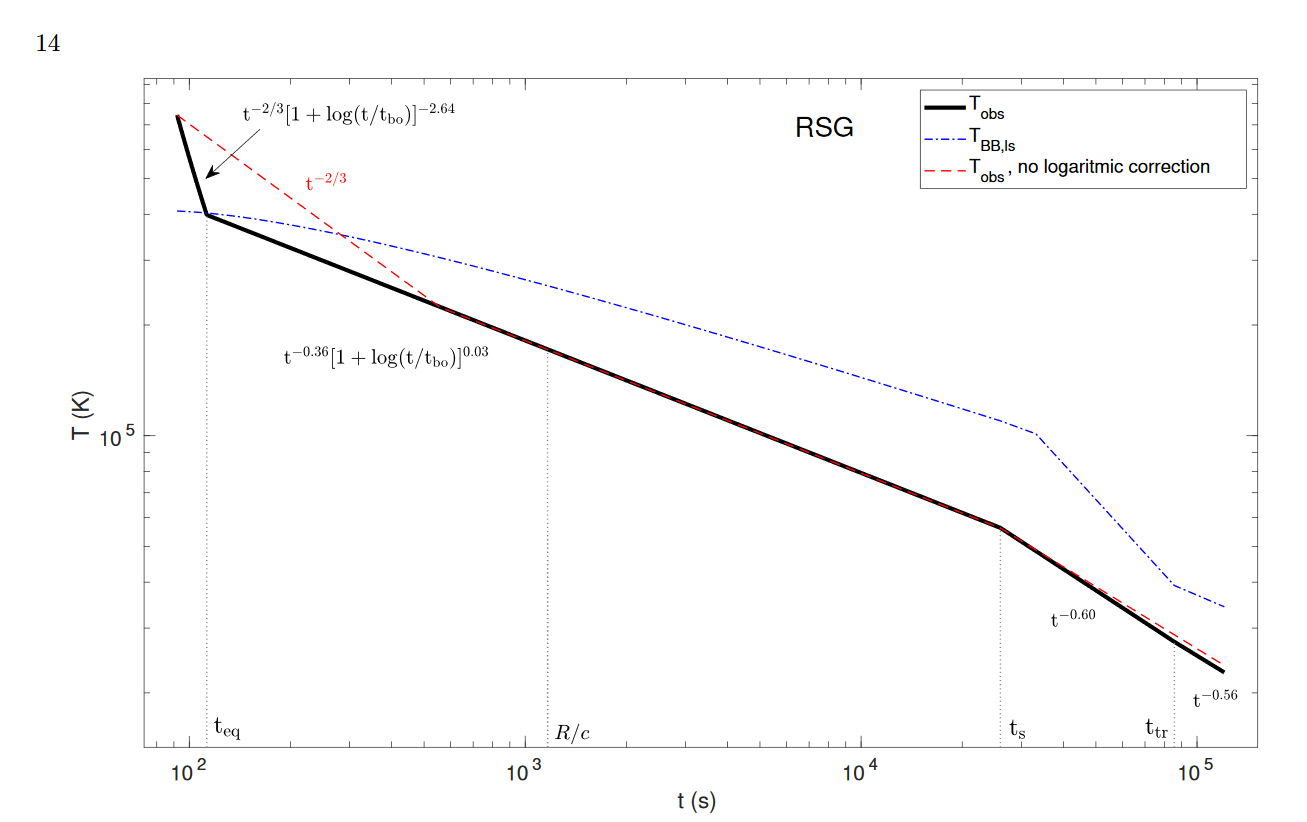
Red Supergiant,
stronger explosion
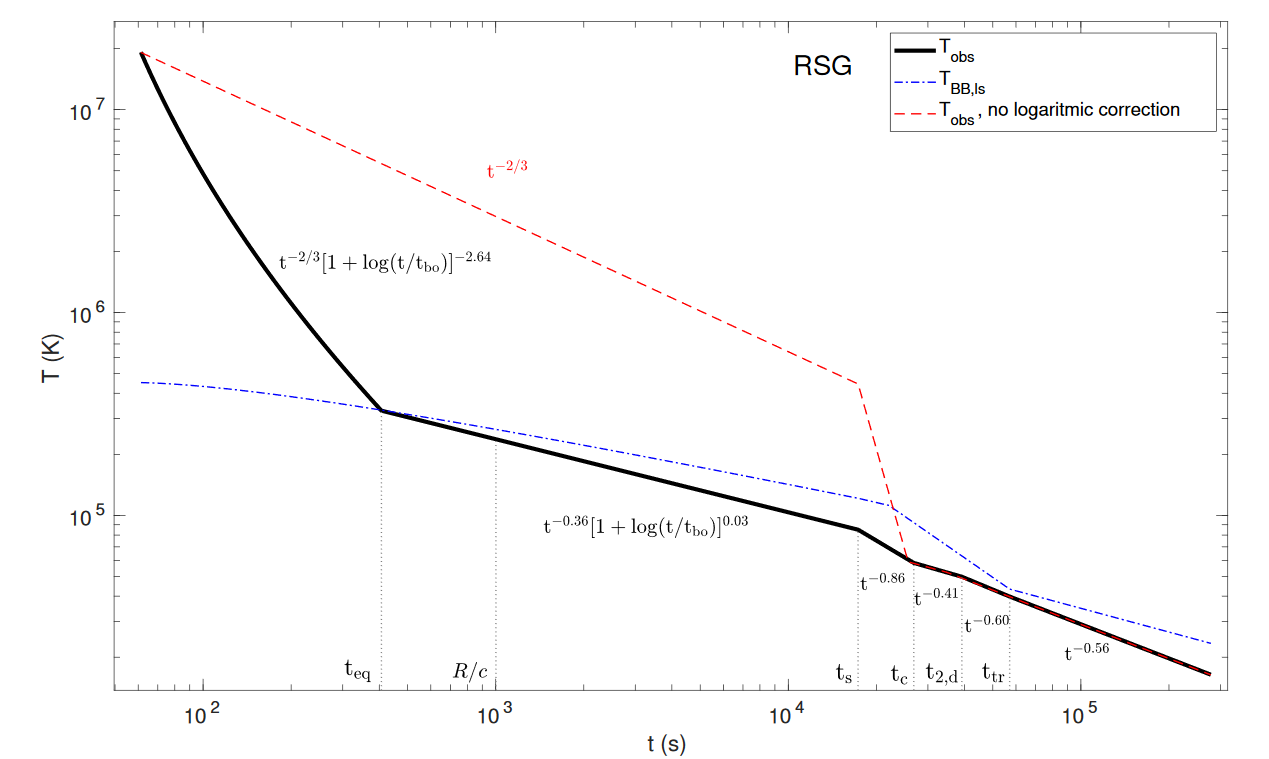
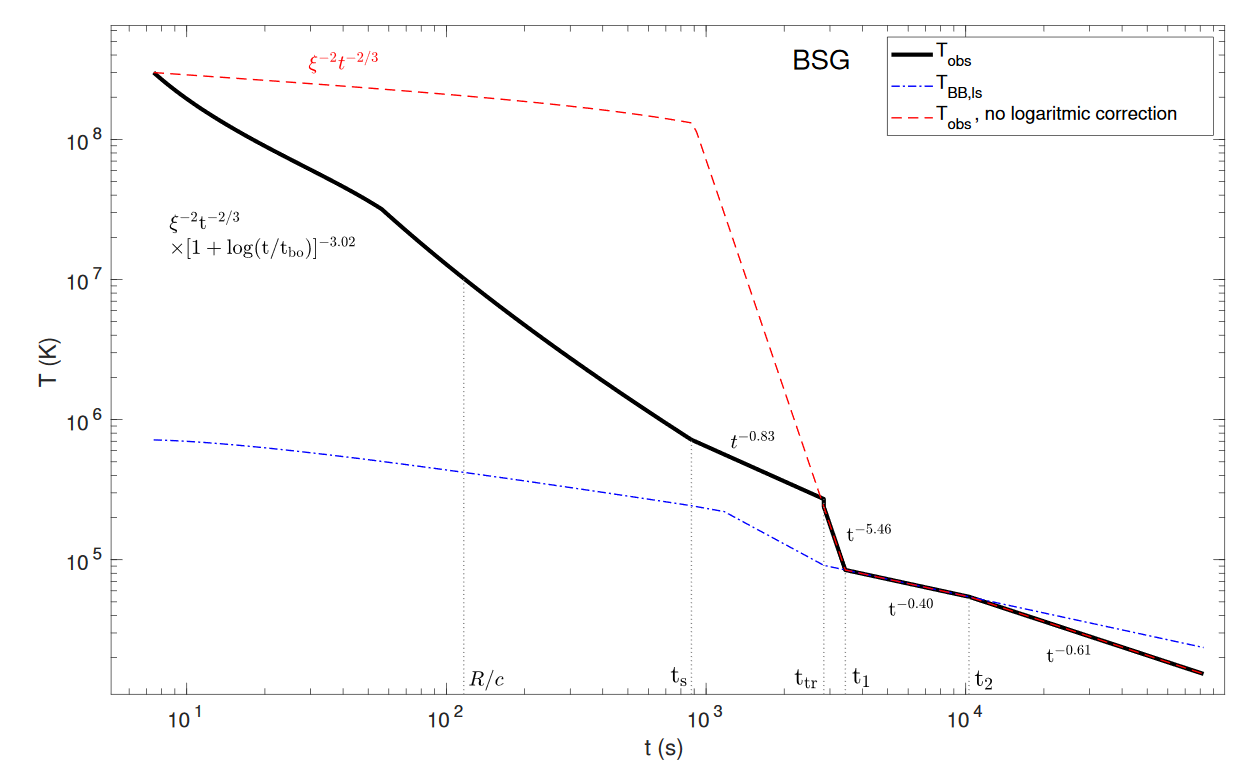
Blue Supergiant
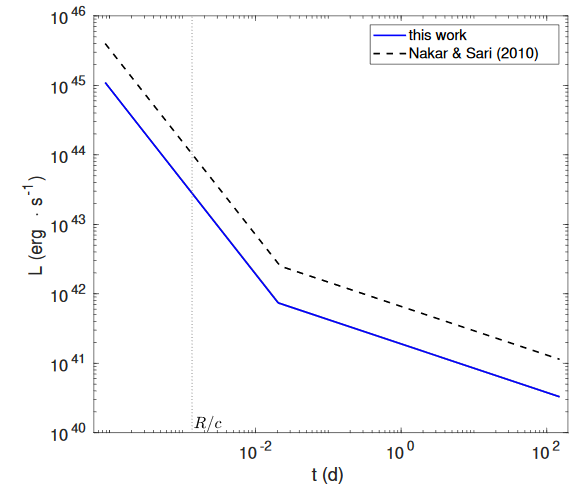
Blue Supergiant
Wolf Rayet
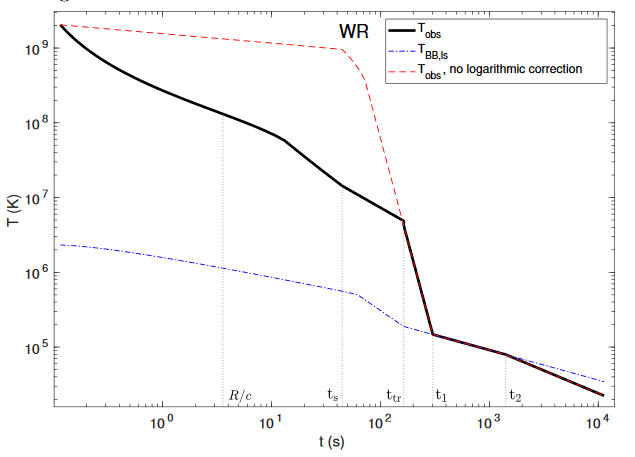
Logarithmic correction to planar shock breakout
By almog yalinewich
