Almog Yalinewich
Stability of the 3 body problem
Possible Fates of Star + 2 Planets
Stable evolution
Plunge into the star
Unbinding from star
"Collision"
Hill Stability
Why not use an N-body integrator?
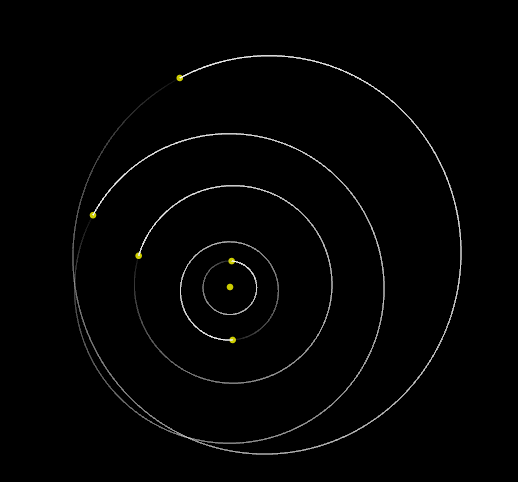
Numerical Errors
Time
Large Survey
Rebound
Introducing Angular Momentum Deficit
Hill stability guaranteed if
\mathcal{L} < C
\mathcal{L} = \gamma \alpha \left(1-\sqrt{1-e_1^2}\cos i_1\right) +1 - \sqrt{1-e_2^2} \cos i_2
C = \gamma \sqrt{\alpha} + 1 - \left(\gamma+1\right)^{3/2} \sqrt{\frac{\alpha}{\alpha+\gamma} \left(1+\frac{3^{3/4} \varepsilon^{2/3} \gamma}{\left(1+\gamma\right)^2}\right)}
\alpha = \frac{a_1}{a_2}
\gamma = \frac{m_1}{m_2}
\varepsilon = \frac{m_1+m_2}{m_0}
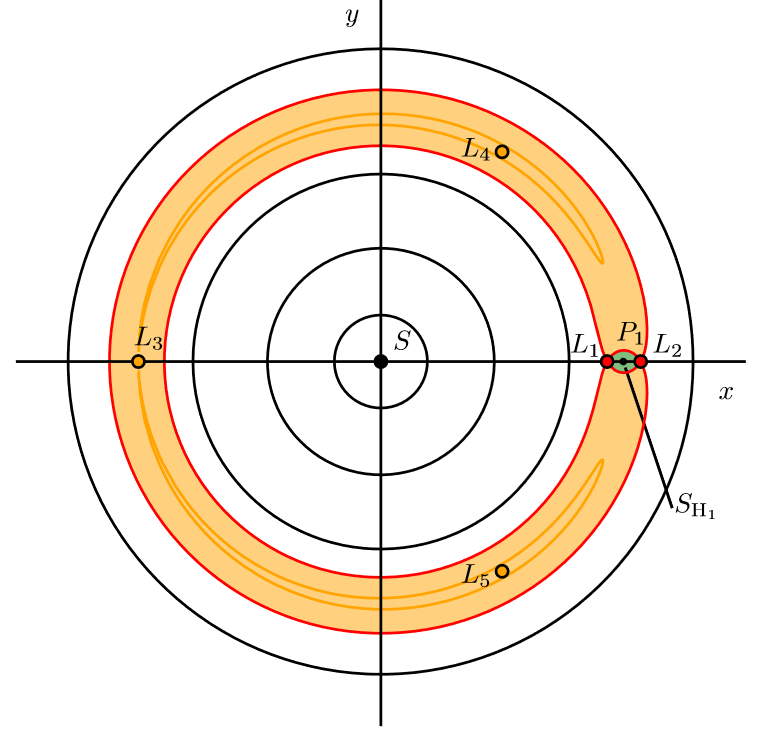
Schematic
m_2
m_1
m_0
a_2
a_1
Numerical Experiments
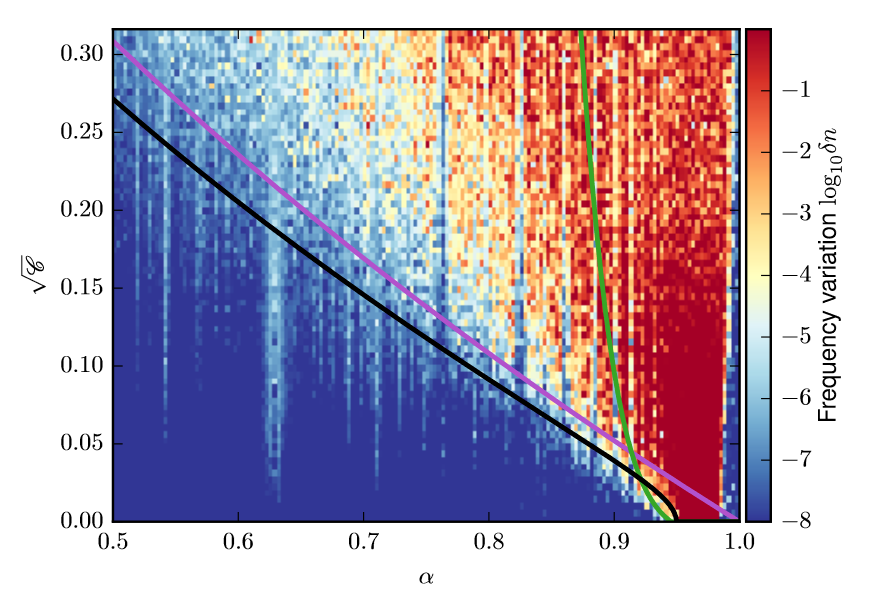
Numerical Experiments cont'd
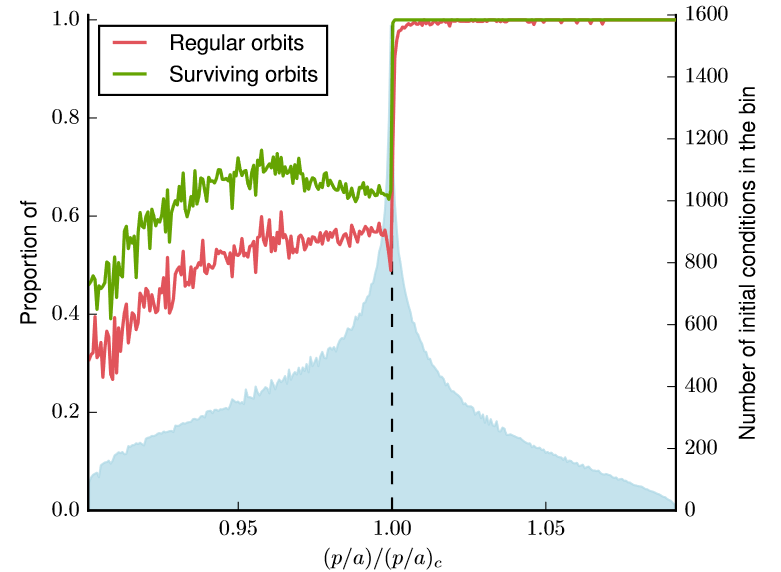
Derivation
Sundman Inequality
T = \frac{1}{2} \sum^N_{i=1} m_i \mathbf{v}_i^2
Let us consider an ensemble of particles
m_i, \mathbf{r}_i, \mathbf{v}_i
(masses, radii and velocities)
Kinetic energy
I = \frac{1}{2} \sum^N_{i=1} m_i \mathbf{r}_i^2
Moment of inertia
\mathbf{J} = \sum^N_{i=1} m_i \mathbf{r}_i \times \mathbf{v}_i
Angular Momentum
Sundman Inequality 2
T = \frac{1}{2} \sum^N_{i=1} \mathbf{V}_i^2
Absorb mass
\mathbf{R}_i = \sqrt{m_i} \mathbf{r}_i, \mathbf{V}_i = \sqrt{m_i} \mathbf{v}_i
Kinetic energy
I = \frac{1}{2} \sum^N_{i=1}\mathbf{R}_i^2
Moment of inertia
\mathbf{J} = \sum^N_{i=1} \mathbf{R}_i \times \mathbf{V}_i
Angular Momentum
Sundman Inequality 3
\dot{I}^2 = \left(\sum^N_{i=1}\mathbf{R}_i \cdot \mathbf{V}_i \right)^2 < \sum_{i=1}^{N} \left(\mathbf{R}_i \cdot \mathbf{V}_i \right)^2 = \sum_{i=1}^{N} \sum_{j=1}^{N} \left(\mathbf{R}_i \cdot \mathbf{V}_j \right)^2 \delta_{ij} <\sum_{i=1}^{N} \sum_{j=1}^{N} \left(\mathbf{R}_i \cdot \mathbf{V}_j \right)^2
Cauchy Schwartz Inequality
Sundman Inequality 4
\mathbf{J}^2 = \left(\sum^N_{i=1}\mathbf{R}_i \times \mathbf{V}_i \right)^2 < \sum_{i=1}^{N} \left(\mathbf{R}_i \times\mathbf{V}_i \right)^2 = \sum_{i=1}^{N} \sum_{j=1}^{N} \left(\mathbf{R}_i \times \mathbf{V}_j \right)^2 \delta_{ij} <\sum_{i=1}^{N} \sum_{j=1}^{N} \left(\mathbf{R}_i \times \mathbf{V}_j \right)^2
Cauchy Schwartz Inequality
Sundman Inequality 5
\dot{I}^2 + \mathbf{J}^2 < \sum_{i=1}^{N} \sum_{j=1}^{N} \left[\left(\mathbf{R}_i \cdot \mathbf{V}_j\right)^2 +\left(\mathbf{R}_i \times \mathbf{V}_j\right)^2 \right] = \sum_{i=1}^{N} \sum_{j=1}^{N} R_i^2 V_j^2 = 4 I T
\cos^2 \theta + \sin \theta^2 = 1
Sundman Inequality 6
4IT = 4I\left(H-U\right)>\dot{I}^2+\mathbf{J}^2
H = - \frac{G B}{2 a}
4I H> \mathbf{J}^2+4 IU
I = \frac{1}{2} \frac{B \rho^2}{M}
J^2 = \frac{G B^2 p}{M}
B = m_0 m_1 + m_1 m_2 + m_2 m_0
M = m_0 + m_1 + m_2
\frac{\rho}{\nu} >\frac{p}{2 \rho} + \frac{\rho}{2 a}
U = -\frac{G B}{\nu}
Angular Momentum Deficit
Maximum value of right hand side
\frac{\rho}{\nu} >\frac{p}{2 \rho} + \frac{\rho}{2 a}
\frac{\partial}{\partial \rho} \left(\frac{p}{2 \rho} + \frac{\rho}{2 a}\right) = 0 \Rightarrow \rho_{\min}=\sqrt{p a}
\frac{\rho}{\nu} >\frac{p}{2 \rho} + \frac{\rho}{2 a} > \frac{p}{a}
Angular Momentum Deficit 2
x_{1,2} = 1 \pm \sqrt[3]{\varepsilon/3}
\varepsilon = \frac{m_1 + m_2}{M} \ll 1
\frac{\rho_{1,2}^2}{\nu_{1,2}^2} \approx 1 + 3^{3/4} \varepsilon^{2/3} \frac{\gamma}{\left(1+\gamma\right)^2}
\gamma = \frac{m_1}{m_2}
Angular Momentum Deficit 3
\frac{p}{a} > \frac{\rho_{1,2}^2}{\nu_{1,2}^2} \approx 1 + 3^{3/4} \varepsilon^{2/3} \frac{\gamma}{\left(1+\gamma\right)^2}
Stability is guaranteed if
\frac{p}{a} = - \frac{2 J^2 M H}{G^2 B^3}
Recalling the definitions
Angular Momentum Deficit 4
H \approx -\frac{1}{2} \frac{G m_0 m_1}{a_1} - -\frac{1}{2} \frac{G m_0 m_2}{a_2}
J \approx J_z = m_1 \sqrt{G m_0 a_1 \left(1-e_1^2\right) }\cos i_1 + m_2 \sqrt{G m_0 a_2 \left(1-e_2^2\right) } \cos i_2
\frac{p}{a} \approx \frac{1+\varepsilon}{\varepsilon^3 \left(1+\gamma\right)^3 \left(1+\frac{\varepsilon \gamma}{\left(1+\gamma\right)^2}\right)^3} \left(1+\frac{\gamma}{\alpha}\right) \cdot
\left(\gamma \sqrt{\alpha} \sqrt{1-e_1^2} \cos i_1 - \sqrt{1-e_2^2} \cos i_2 \right)
Conclusion
Hill stability criterion for
m_0 \gg m_1, m_2
e_1, e_2 \ll 1
\gamma = \frac{m_1}{m_2}
arbitrary
and
i_1, i_2
angular momentum deficit
By almog yalinewich
