Disintegrating Bullet Model for Null Periods in GRBs
Almog Yalinewich - RandoAstro -13.2.20
Also experiments!
If you've seen one GRB,
you've seen just one GRB
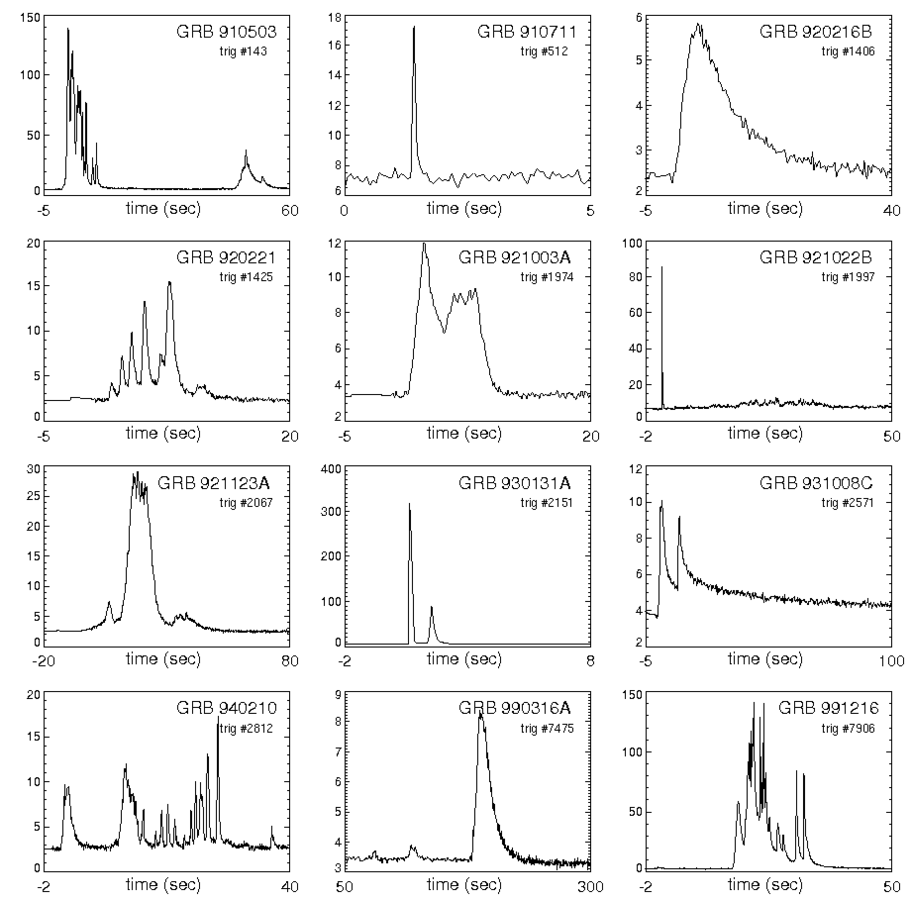
null periods
LGRB - SN association
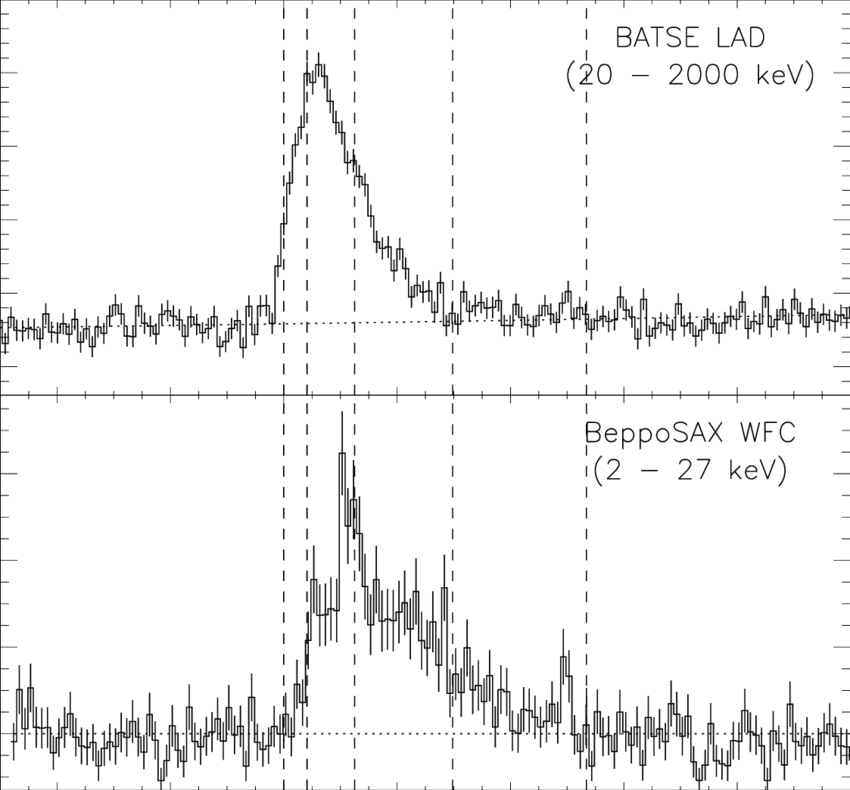
SN 1998bw
GRB 980425
Collapsars
Collapsars
Illustration
Acceleration
Rayleigh Taylor Instability
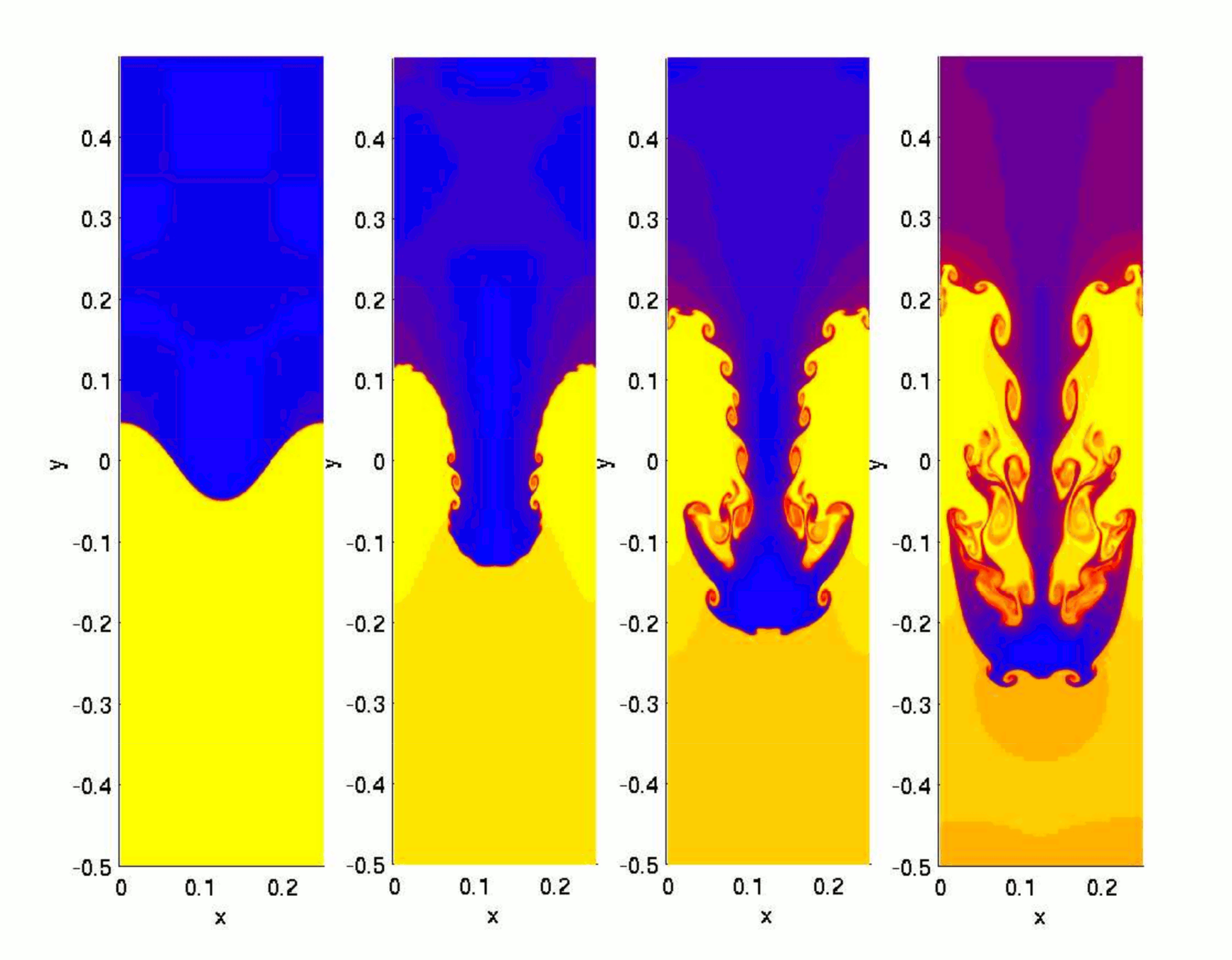
Disintegrating Bullet Model
Mathematical Model
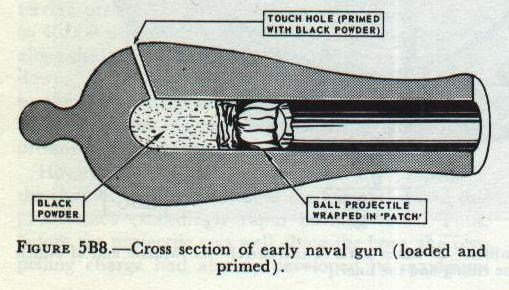
Projectile motion
Instability evolution
Newtonian Projectile Motion
m\frac{d v}{d t} = A p
Equation of motion
Velocity pressure relation? Riemann invariants
J_+ = v + \frac{2}{\gamma - 1} c_s
p \propto \rho^{\gamma}
Isentropic relation
v{\left(t \right)} = \frac{2 c_0}{\gamma-1} \left(1 - \left( \frac{A p_{0} t}{2 m c_0} \left(\gamma + 1\right)^{3} + \left(\gamma +1\right)^2\right)^{\frac{1 - \gamma}{\gamma + 1}}\right)
Sound speed
c_s^2 = \gamma \frac{p}{\rho}
Riemann Invariants
Acoustic relation
dv = \frac{dp}{c_s \rho}
Extrapolation
\Delta v = \int\frac{dp}{c_s \rho}
Ideal gas
J_+ = v + \frac{2 c_s}{\gamma-1}
Rayleigh Taylor Growth Rate
\Gamma \approx \sqrt{k a}
High k - grow fast and saturate fast
Low k - grow slow
optimal k determined by bullet width
Bullet Width Evution
x
p
contact with pressure behind
Bullet expands adiabatically after the first shock
Breakup Time
\Gamma t \approx 1
but in this case this is independent of time
4 S^{- \frac{1}{\gamma}} c_{0}^{\frac{2 \gamma \left(\gamma^{2} + 2 \gamma + 1\right)}{\gamma^{3} + \gamma^{2} - \gamma - 1}} p_{0}^{- \frac{\gamma^{3} + 1}{\gamma \left(\gamma^{2} - 1\right)}} \left(\frac{\rho_{0}}{\gamma}\right)^{\frac{1}{\gamma - 1}} \left(\gamma + 1\right)^{-2}
Either happens in the very beginning, or never
Perturbation growth
Enter Relativity!
Relativistic Riemann Invariant
J_+^p = \ln \gamma + \frac{\sqrt{\eta-1}}{\eta} \ln p
J_+^s = \ln \gamma + \frac{\sqrt{\eta-1}}{\eta} \ln p + \frac{2\sqrt{\eta-1}}{{1+\sqrt{\eta-1}}} \ln t
Even in spherical geometry
Acceleration Transformation
x = \beta_0 t + a t^2/2
\gamma_0 \begin{bmatrix}
1 & -\beta_0 \\
-\beta_0 & 1
\end{bmatrix} \begin{bmatrix}
t\\
\beta_0 t + a t^2/2
\end{bmatrix} \approx
\begin{bmatrix}
t/\gamma_0\\
\gamma_0 a t^2/2
\end{bmatrix}
Motion with uniform acceleration
Lorentz boost to instantaneously comoving frame
Rest frame quantities
t'=t/\gamma_0, a'=a \gamma_0^3
Opening Angle
\theta \approx \frac{1}{\gamma}
Relativistic beaming
Wide jets
\alpha > \gamma^{-1} \Rightarrow \alpha = \rm cons
Narrow jets
\alpha < \gamma^{-1} \Rightarrow \alpha = \gamma^{-1}
Instability Growth
\Gamma = \sqrt{k a \frac{\rho c^2}{p}}
Relativistic inertia effect pm growth rate
Breakup time
t' \Gamma \approx 1
Grows with time!
Application
t \approx 10^3 \, {\rm s} \left(\frac{\gamma_i}{10}\right)^{1.3} \left(\frac{m}{10^{-8} M_{\odot}}\right)^{0.27}
Using typical values, breakup time in the lab frame
Observer time
t_o \approx \frac{t}{\gamma_i^2} \approx 10s
\times \left(\frac{t_i}{100 \, rm s}\right)^{0.2} \left(\frac{\alpha}{0.1}\right)^{-0.53} \left(\frac{\rho_a}{10^{-9} \, rm g/cm^3}\right)^{-0.27}
disintegrating bullet
By almog yalinewich
