Flow of Gas around the Galactic Centre
Almog Yalinewich
Introduction
Journey to the Galactic Centre
Nuclear Star Cluster
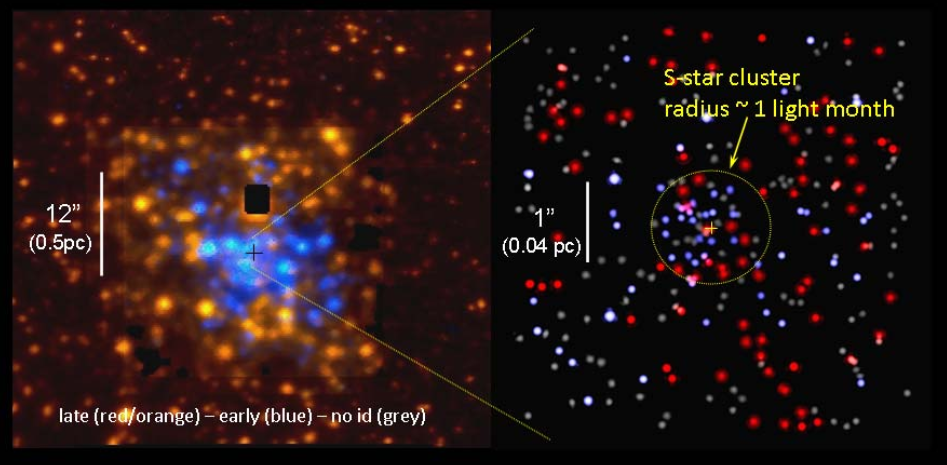
Wind Emitting Stars

Chandra view of the Galactic Centre
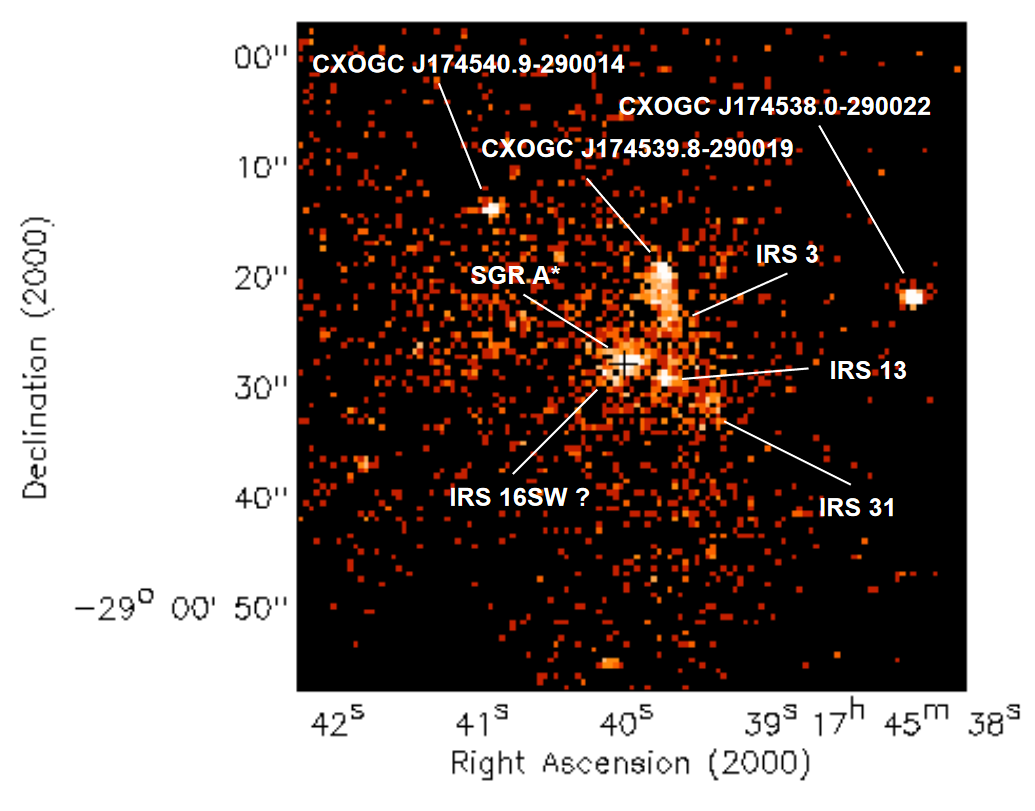
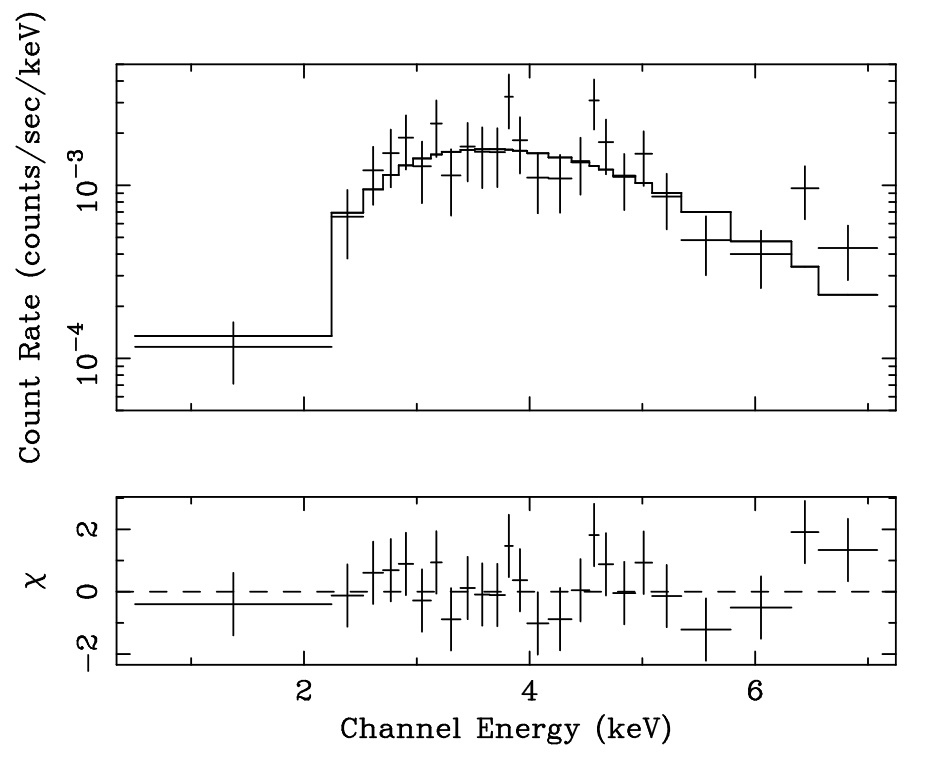
Simplified Model

Other Galactic Centres
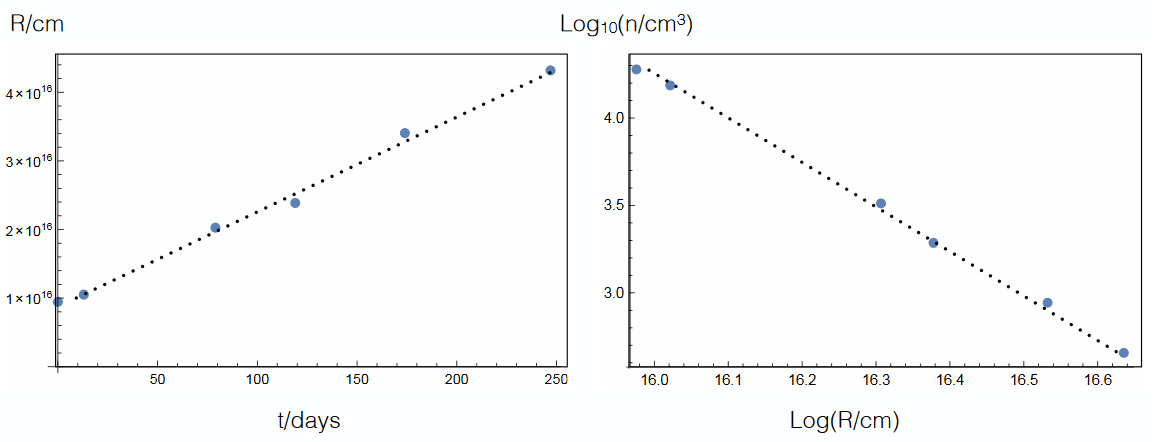
Theoretical Model
Conservation of Mass

Conservation of Energy

Conservation of Momentum
Integrated Forms
Stagnation radius
Mass conservation
Energy conservation
Dimensionless Form
Analytic Solution
Generic Case
Mach number ODE
Wrong
Right
Inner Asymptote
Always supersonic
Boundary condition: finite when
Inner Asymptote
Independent of
Mass dominated by stagnation radius
Outer Asymptote
No steady state solution when
Easiest to understand for the case
Supersonic when
Outer Asymptote
Hydrodynamic Profiles
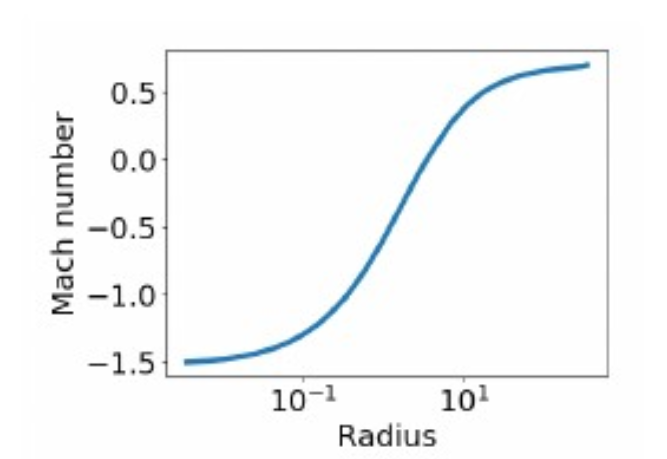
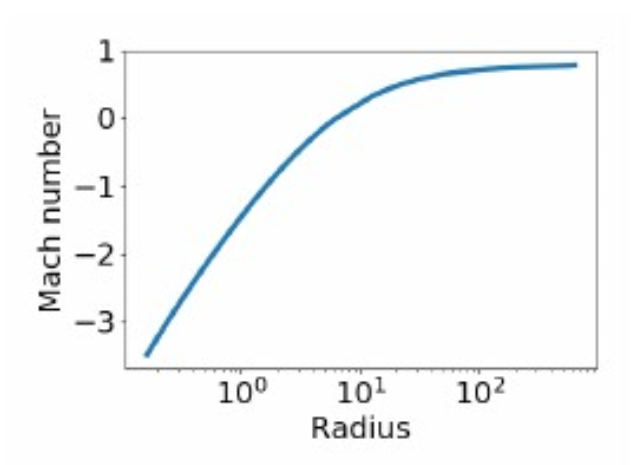
Hydrodynamic Profiles
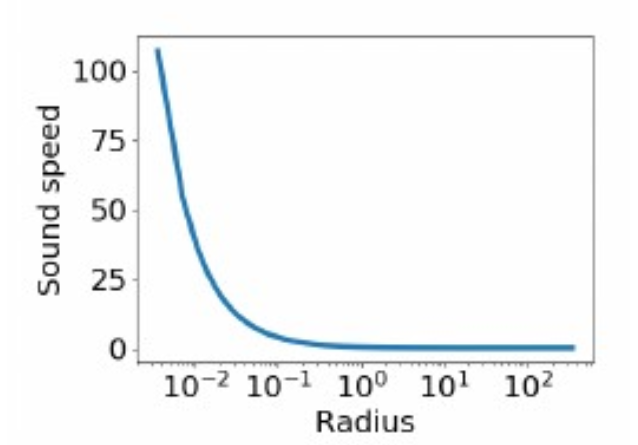
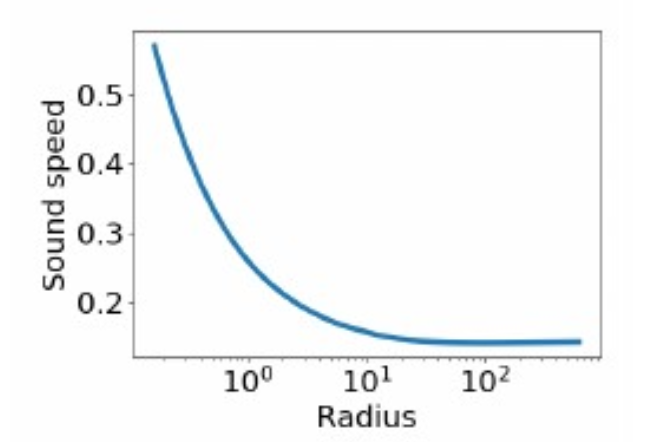
Hydrodynamic Profiles
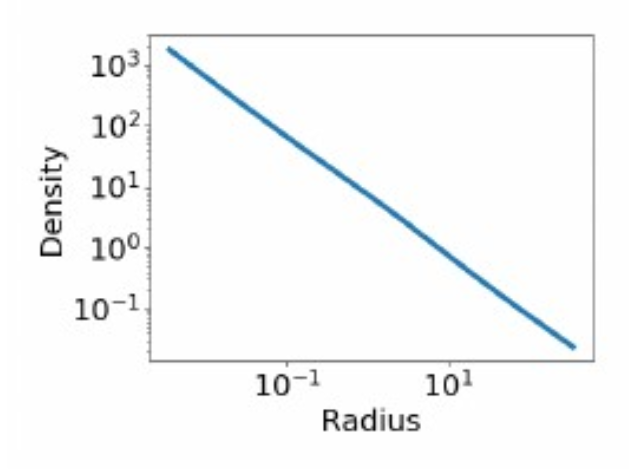
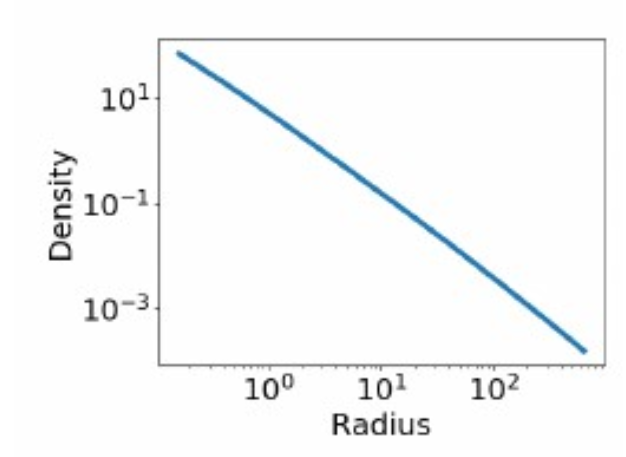
Truncation
Steady state always exists if mass injection is truncated
Truncation 2
Truncation 3
Truncation 4
Radiation
Bremsstrahlung
Truncation necessary to avoid divergence
Synthetic Spectrum
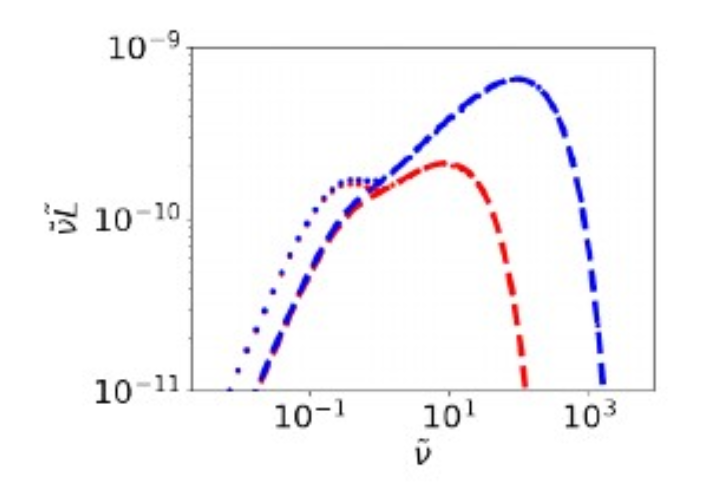
Retrieving the Mass accretion rate
Applications
Milky Way Galactic Centre
Density Comparison

Data favours
From Quataert 2004
Surface Brightness

data favours
Surface Brightness 2
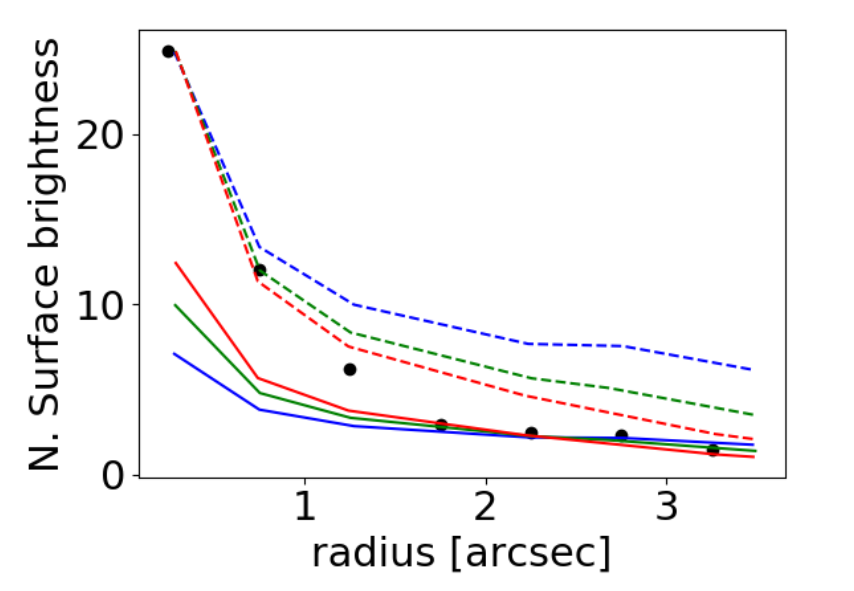
Different normalisation
All models agree
outside Chandra PSF
Unresolved central source?
Stellar Density
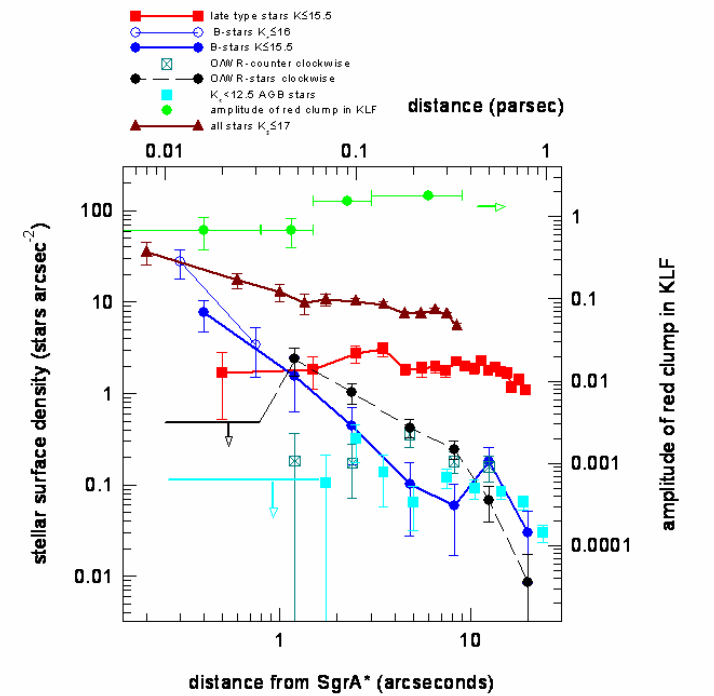
Genzel et al 2010
Other Galactic Centres
Swift 1644+57
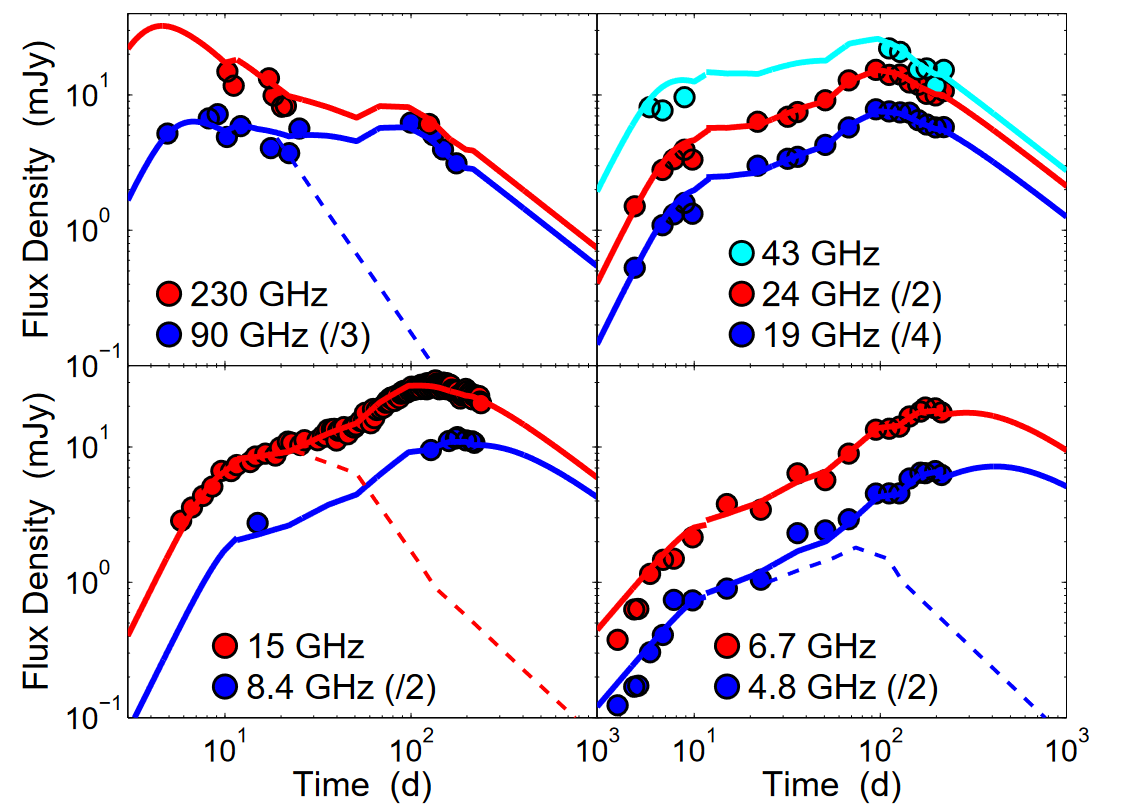
Achromatic break
at 10 days
Tidal Disruption Event Jet
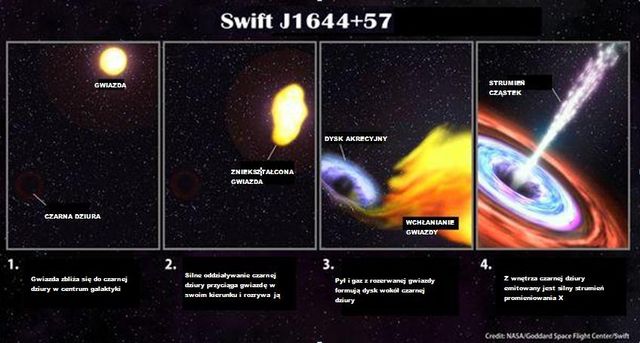
Jet Break?

Break when reverse shock
reaches jet base?
Break when swept up mass is comparable to jet energy?
Density Break?
Break radius
fallback rate implies
Bondi radius
Truncation radius?
Conclusion
Steady state, smooth, spherically symmetric flow model
prediction for spectrum from Bremsstrahlung
Resolve conflicting results for SGR A*
Proposition for achromatic breaks in TDEs
Flow of Gas around the Galactic Centre TAU
By almog yalinewich
Flow of Gas around the Galactic Centre TAU
- 382



