Gradient Descent and the Edge of Stability
Amin
April 2023
Gradient Descent and the Edge of Stability
Amin
April 2023

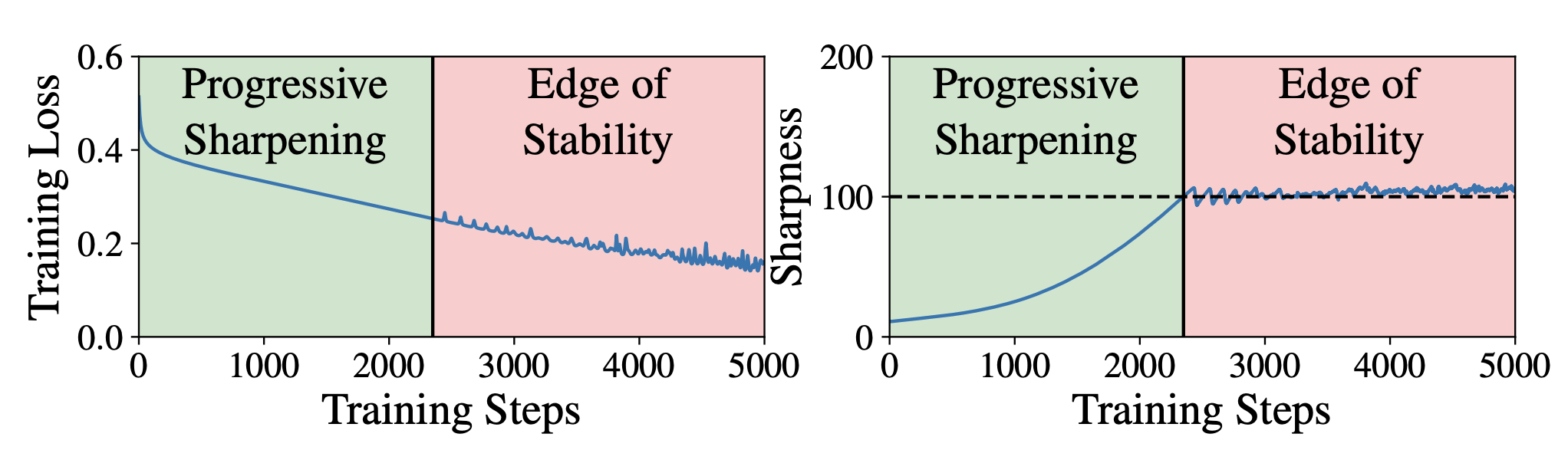
Stability?
- Let \(\ell: \mathbb{R}^P \to \mathbb{R}\) be continuously differentiable and \(L\)-smooth.
- Consider gradient descent on \(\ell\) with a step size of \(\eta\).
- Descent Lemma says:
- Proof: When the function is L-smooth, max eigenvalue of hessian is always smaller (or equal) than L.
\ell(\theta_{t+1}) \le \ell(\theta_t) - \frac{\eta (2 - \eta L)}{2} || \nabla \ell(\theta_t)||^2

Self-Stabilization:
- Gradient Descent Implicitly Solves:
- By evolving around the constrained trajectory
- where \(\mathcal{M}\) is:
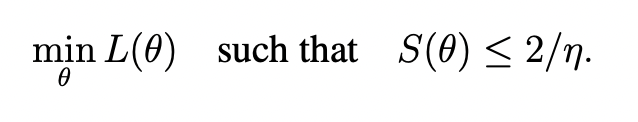

\mathcal{M} = \{ \theta: S(\theta) \le 2 / \eta \wedge \nabla L(\theta) \cdot u(\theta) = 0 \}
Self-Stabilization

Self-Stabilization: Sketch
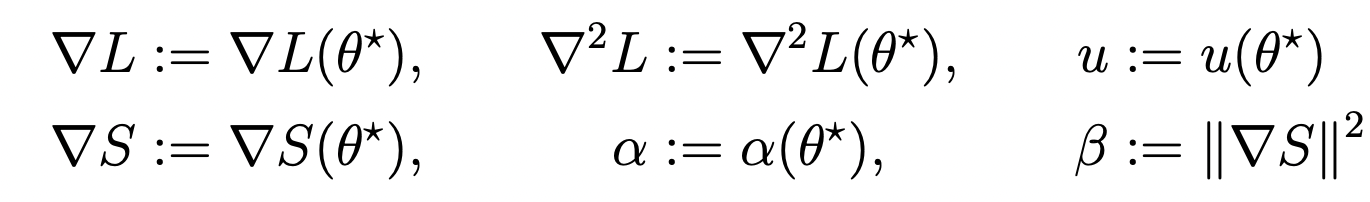
- Assumption 1: Existence of progressive sharpening \(\alpha = \nabla L \cdot \nabla S > 0 \).
- Assumption 2: Eigengap in hessian!
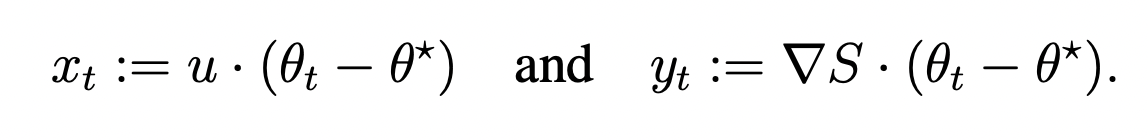
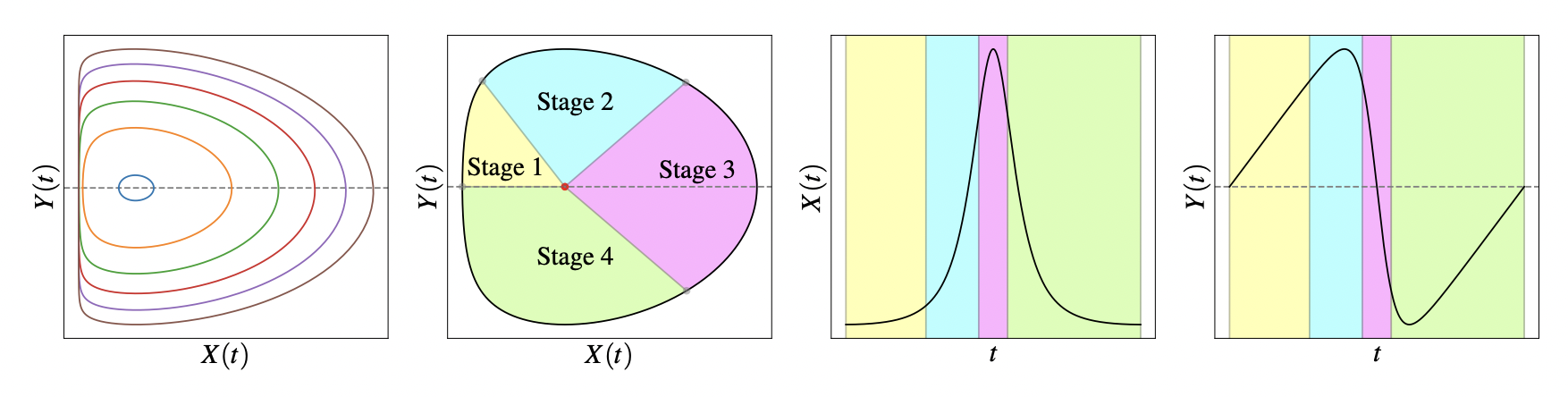
Stage 1
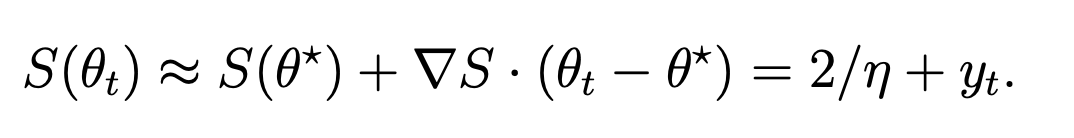
- We can Taylor expand the sharpness around the reference point:

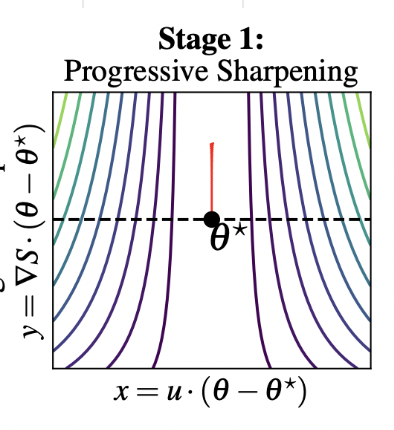
Stage 2

- Note: \(u \cdot \nabla L(\theta_t) \approx S(\theta_t) x_t\) because:
u \cdot \nabla L(\theta^\star) \approx u \cdot \frac{\eta}{2} S(\theta_t) \nabla L(\theta^\star) \approx \frac{1}{2} S(\theta_t) u \cdot \eta \nabla L(\theta^\star)
(I don't understand how they ignore the
factor of 2)
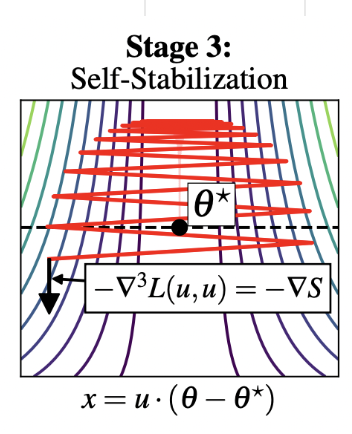
Stage 3

- Hence, adding the cubic term back in the Taylor expansion for \(y_t\), we have:
- Therefore, when \(x_t > \sqrt{2\alpha/\beta}\), sharpness
begins to decrease.
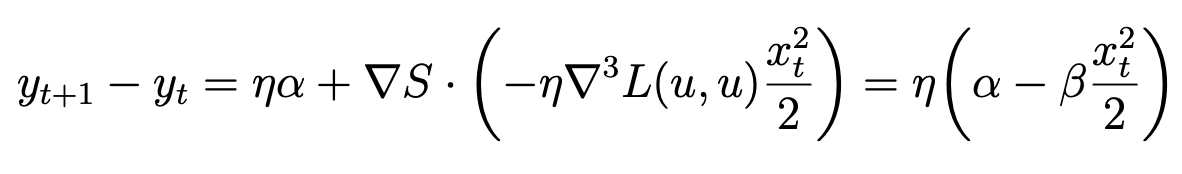
Stage 4

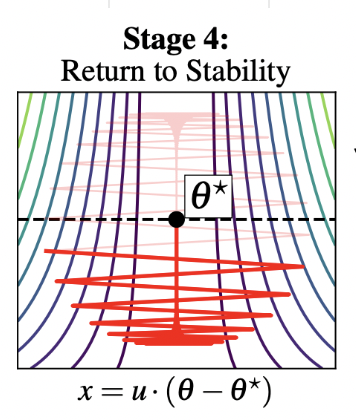
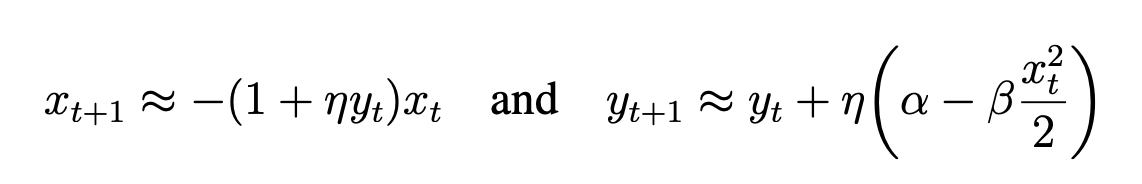
- Hence the full dynamics can be described as:
Self-Stabilization
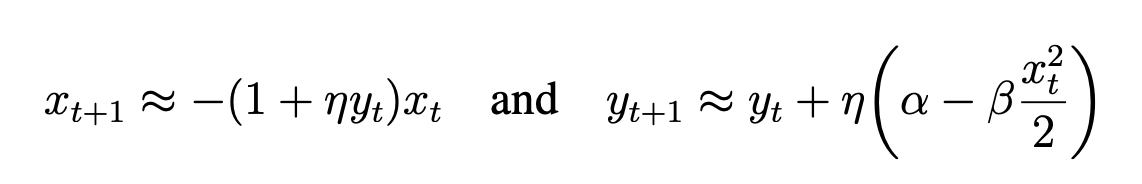
Main Result
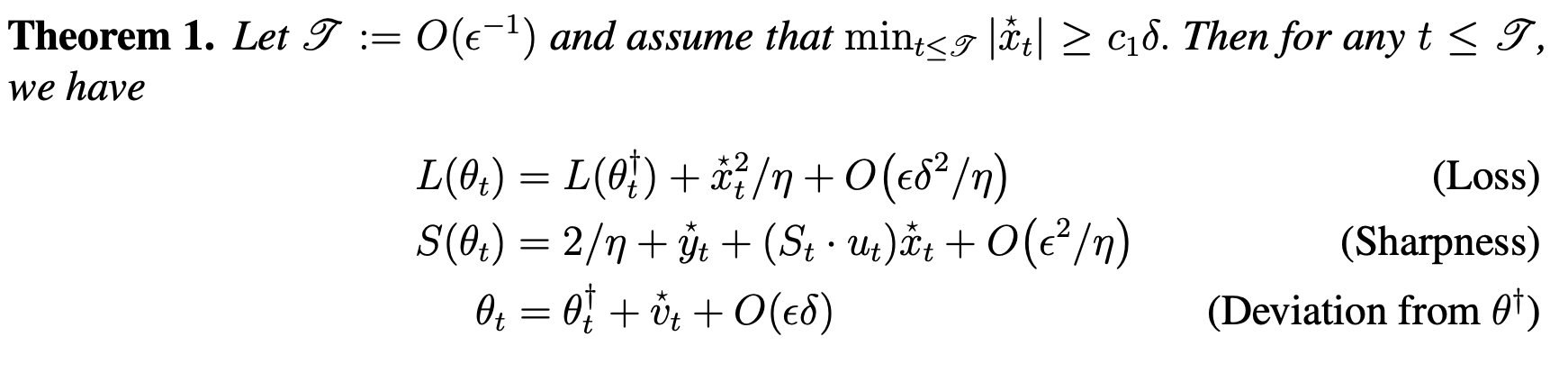
- Takeaway 1: GD's behaviour is not monotonic over short timescales, but is over long timescales.
- Takeaway 2: GD is guaranteed to not increase training loss over long timescales, no matter how non-convex the loss is.
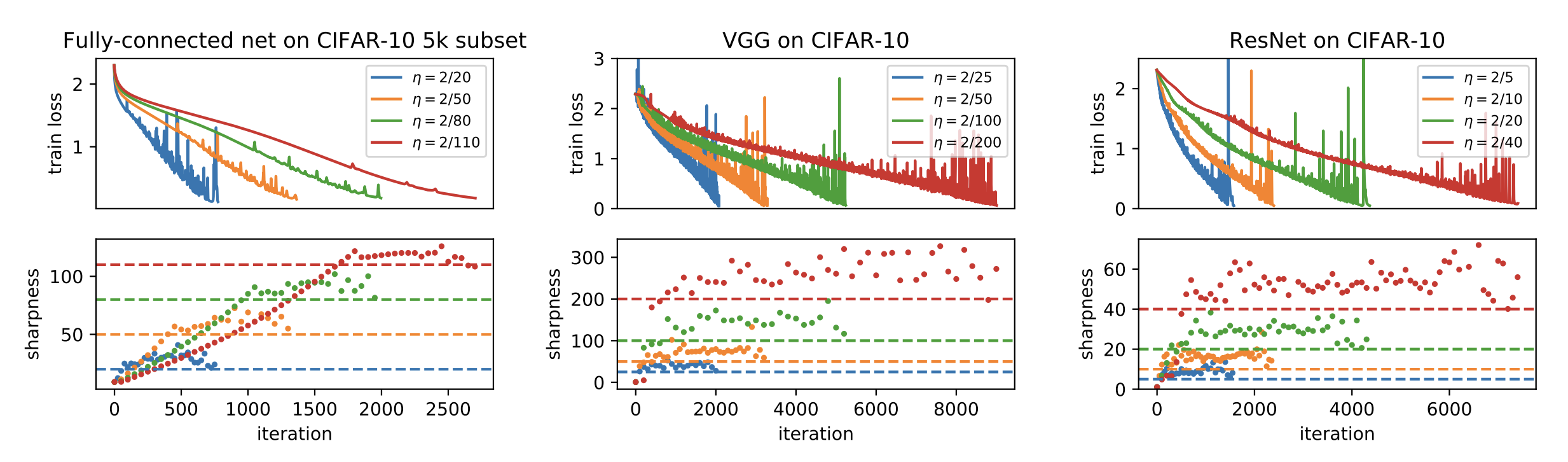
Experiments
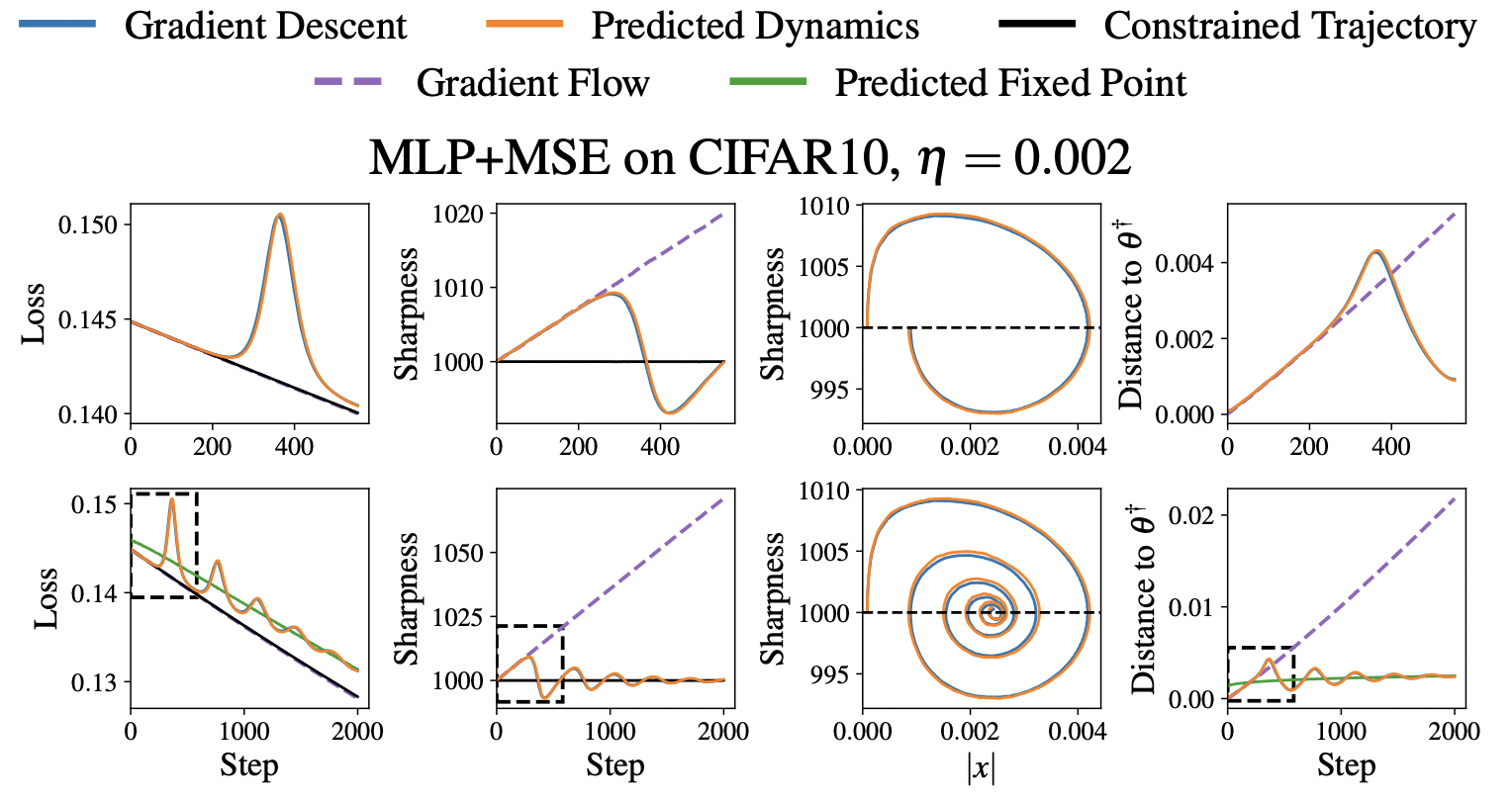
Experiments
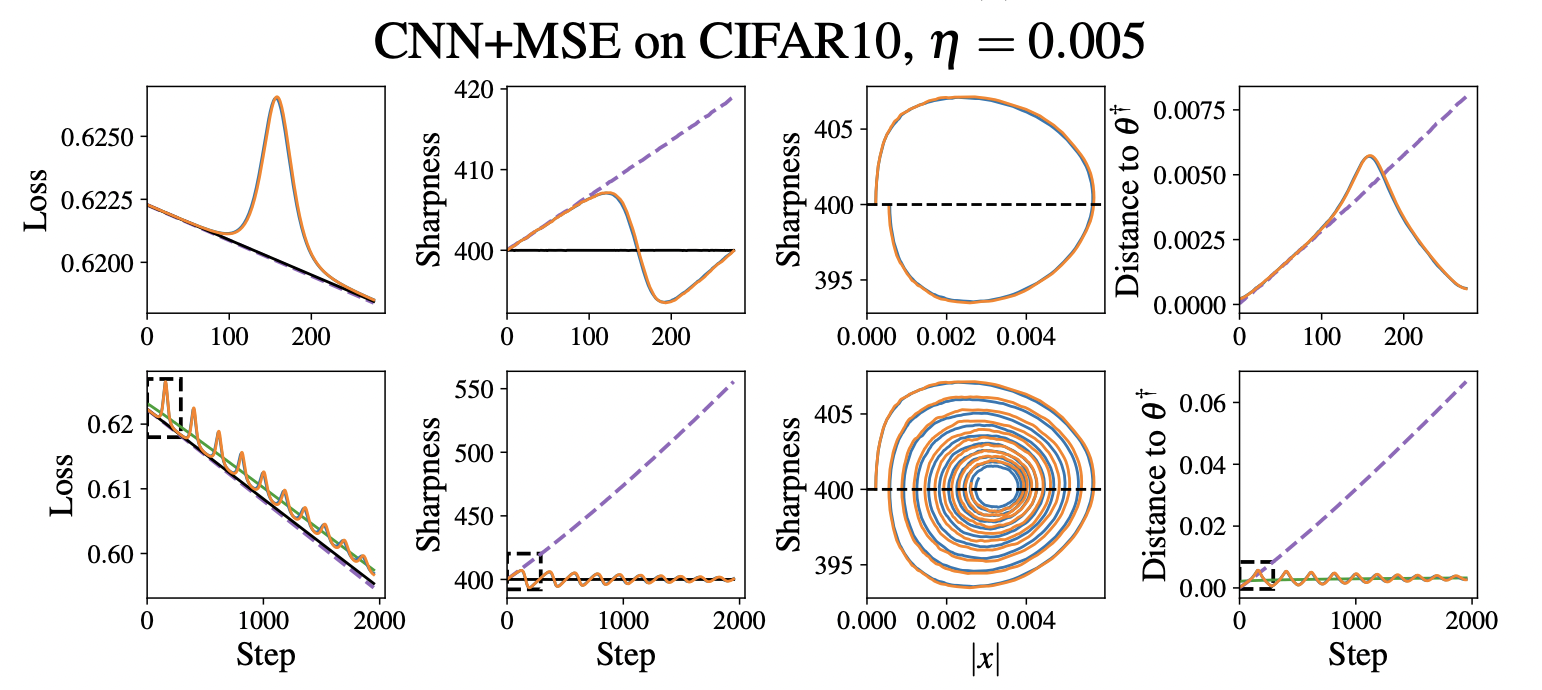
Limitations
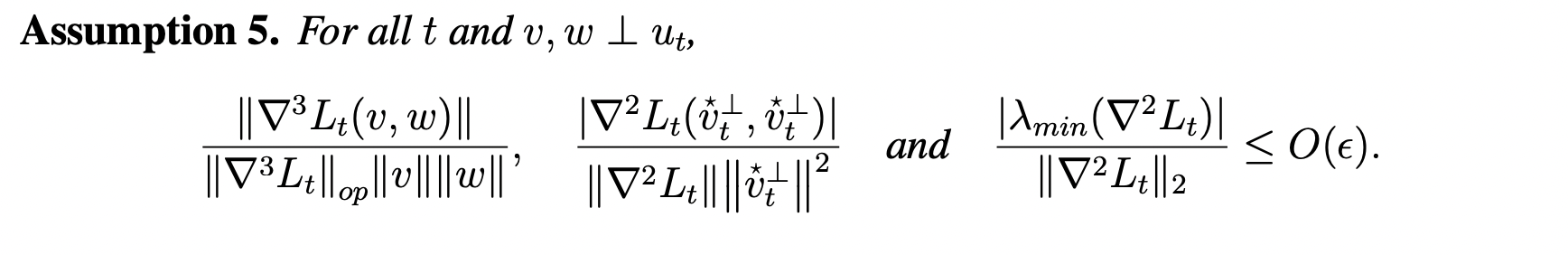
- Assumption 5 in the paper is certainly not true for almost all the practical models. But it can be broken down to multiple more-manageable pieces.
- Assumption 4 is extremely strong, and it directly hints at self-stabilization.
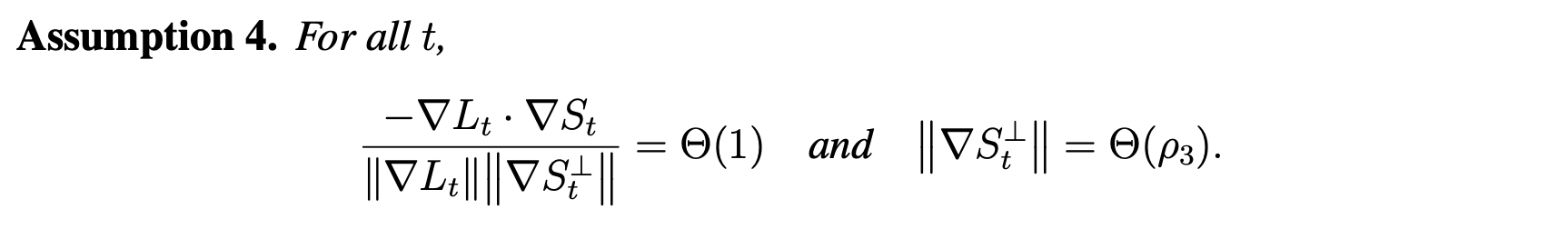
Proof Idea
-
The proof idea is to analyze the the constrained update's trajectory along the directions of velocity of sharpness and top eigenvector:
- And bounding the displacement using a cubic Taylor-expansion (and strong assumptions to make it work :p)
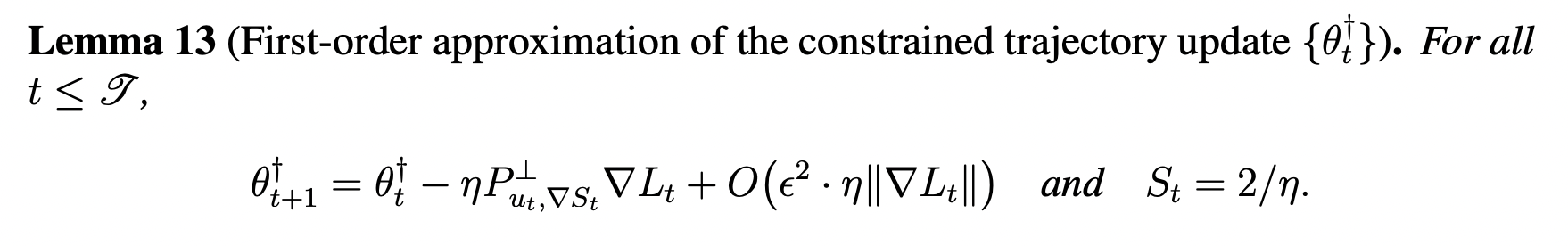

Extension: Multiple Unsabilities

Thank You!
Copy of brain_march_23
By Amin Mohamadi
Copy of brain_march_23
- 383



