A tale of ∞-wide neural networks
Mohamad Amin Mohamadi
September 2022
Math of Information, Learning and Data (MILD)
Outline
- The Neural Tangent Kernel
- Training dynamics of ∞-wide neural networks
- Approximating the training dynamics of finite neural networks
- Linear-ized neural networks
- Applications of the Neural Tangent Kernel
(Our work included)
- Approximating the Neural Tangent Kernel
(Our work)
1. The NTK
Deep Neural Networks
- Over-parameterization often leads to fewer "bad" local minimas, albeit the non-convex loss surface
- Extremely large networks that can fit random labels paradoxically achieve good generalization error on test data (kernel methods ;-) ?)
- The training dynamics of deep neural networks is not yet characterized
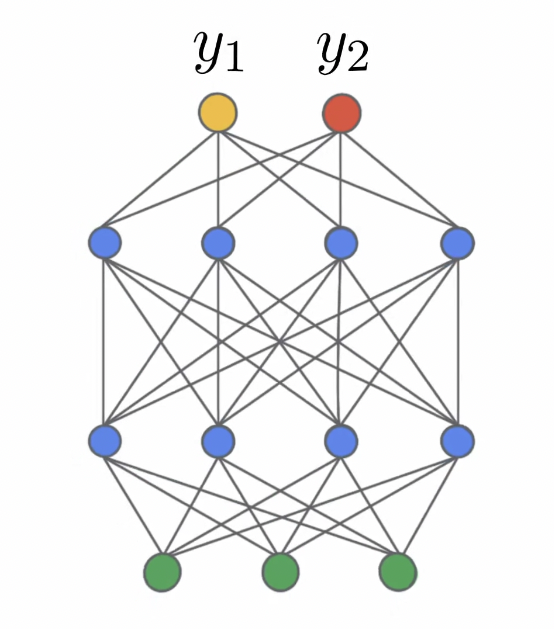
Training Neural Networks
\mathcal F: \{f: \mathbb{R}^{n_0} \to \mathbb{R}^{n_L}\}
\ell: \mathbb{R}^P \to \mathbb{R}
F^{(L)}: \mathbb{R}^P \to \mathcal{F}
p^{in} = \{(x_i, y_i)\}_i \text{ for } i \in [N]
Basic elements in neural network training:
Gradient Descent:
\nabla_\theta \ell(\theta_t) = - \sum_{i=1}^N (f_{\theta_t}(x_i) - y_i) \frac{\partial f_{\theta_t} (x_i)}{\partial \theta}
Training Neural Networks
Idea: Study neural networks in the function space!
Gradient Flow:
\frac{\partial \theta(t)}{\partial t} = - \sum_{i=1}^N (f_{\theta(t)}(x_i) - y_i) \frac{\partial f_{\theta(t)} (x_i)}{\partial \theta}
Change in the function output:
\frac{\partial f_{\theta(t)} (x_i)}{\partial t} = \frac{\partial f_{\theta(t)} (x_i)}{\partial \theta} \frac{\theta(t)}{\partial t}
= -\sum_{j=1}^N (f_{\theta(t)}(x_j) - y_j) \langle \frac{\partial f_{\theta(t)} (x_i)}{\partial \theta}, \frac{\partial f_{\theta(t)} (x_j)}{\partial \theta} \rangle
Hmm, looks like we have a kernel on the right hand side!
Training Neural Networks
\frac{\partial f_{\theta(t)} (x_i)}{\partial t} = -\sum_{j=1}^N (f_{\theta(t)}(x_j) - y_j) K_{\theta(t)}(x_i, x_j)
So:
K_{\theta(t)}(x_i, x_j) = \langle \frac{\partial f_{\theta(t)} (x_i)}{\partial \theta}, \frac{\partial f_{\theta(t)} (x_j)}{\partial \theta} \rangle
where
this is called the Neural Tangent Kernel!
\Longrightarrow f_{\theta(t)}(x) = \underbrace{\sum_{j=1}^N K_{\theta(t)}(x, x_j) f_{\theta(t)}(x_j)}_\text{function of $f_{\theta(t)}(x), x$ at $t$} - \underbrace{\sum_{j=1}^N K_{\theta(t)}(x, x_j) f^*(x_j)}_\text{function of $x$ at $t$}
Training Neural Networks
Arthur Jacot, Franck Gabriel, Clement Hongler
∞-wide networks
- (Theorem 1) For an MLP network with depth L at initialization, with a Lipschitz non-linearity, at the limit of infinitely wide layers, the NTK converges in probability to a deterministic limiting kernel.
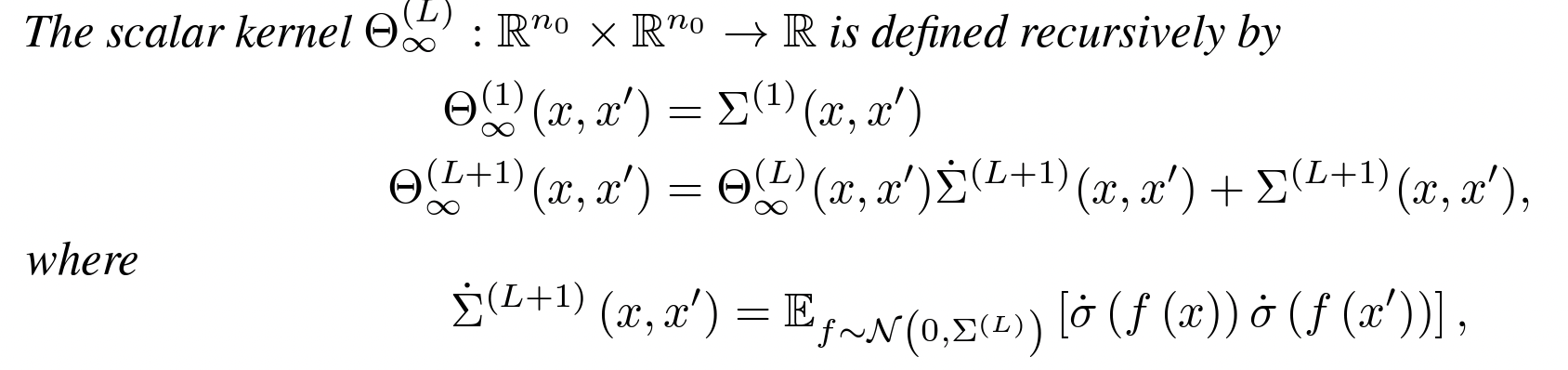
∞-wide networks
- (Theorem 2) For an MLP network with depth with a Lipschitz twice-differentiable non-linearity, at the limit of infinitely wide layers, the NTK does not change during training along the negative gradient flow direction.
K_{\theta(t)}(x_i, x_j) \longrightarrow \mathbb{E} [\langle \frac{\partial f_0 (x_i)}{\partial \theta}, \frac{\partial f_0 (x_j)}{\partial \theta} \rangle] \text{ for all } t
- Now, What does this imply?
∞-wide networks
f_{\theta(t)}(x) = \underbrace{\sum_{j=1}^N K_{\theta(t)}(x, x_j) f_{\theta(t)}(x_j)}_\text{function of $f_{\theta(t)}(x), x$ at $t$} - \underbrace{\sum_{j=1}^N K_{\theta(t)}(x, x_j) f^*(x_j)}_\text{function of $x$ at $t$}
- If the kernel is constant in time, we can solve this system of differential equations! (Stack the training points)
- If the kernel is constant, we can claim global convergence based on the PSD-ness of the limiting kernel (Proven for a general case).
∞-wide networks
f_{\theta(t)} (x) = \sum_{j=1}^N K(x, x_j) \left [ \int_{t'=0}^t \left(f_{t',z}(x_j) - f^*_{S_i, z}(x_j)\right) dt' \right ]_{z} \\
= f_0(x) + K(x, X) K^{-1}(X, X) \left(I - e^{-tK(X, X)} \right) \left( f^*(X) - f_0(X) \right)
Thus, we can analytically characterize the behaviour of infinitely wide (and obviously, overparameterized) neural networks, using a simple kernel ridge regression formula!
As it can be seen in the formula, convergence is faster along the kernel principal components of the data (early stopping ;-) )
= f_0(x) + K(x, X) K^{-1}(X, X) \left(I - e^{-tK(X, X)} \right) \left( f^*(X) - f_0(X) \right)
Finite wide networks
- As we saw, convergence and training dynamics of infinitely-wide neural networks can be captured using a simple kernel regression-alike formula (?)
- Does this have any implication for finite neural networks?
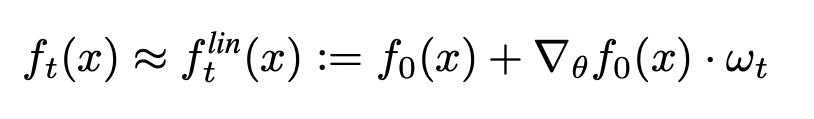
Finite wide networks
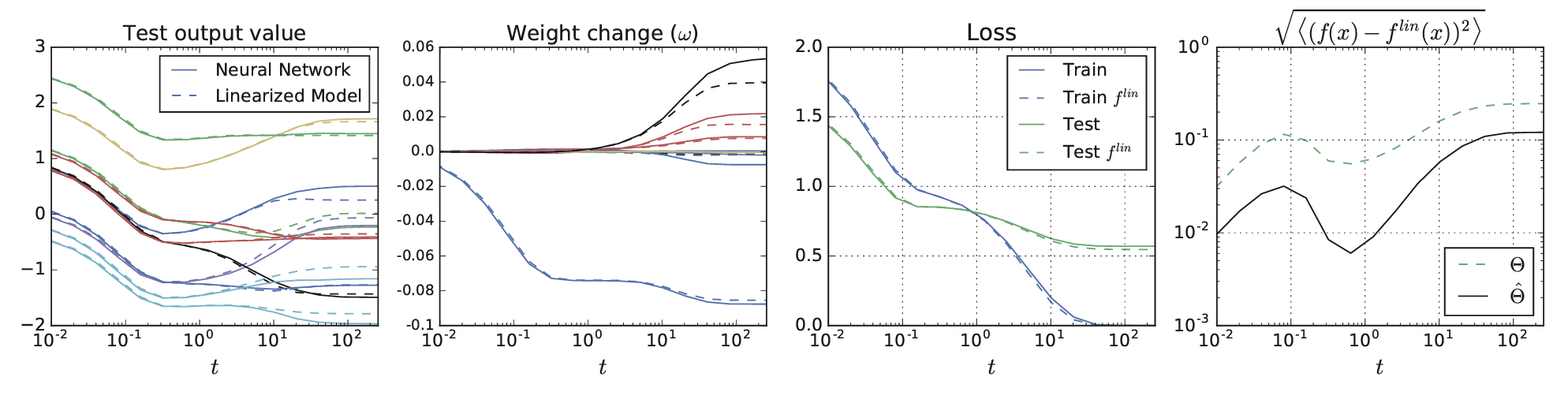
Lee et al. showed that the training dynamics of a linear-ized version of a neural network can be explained using kernel ridge regression with the kernel as the empirical Neural Tangent Kernel of the network:
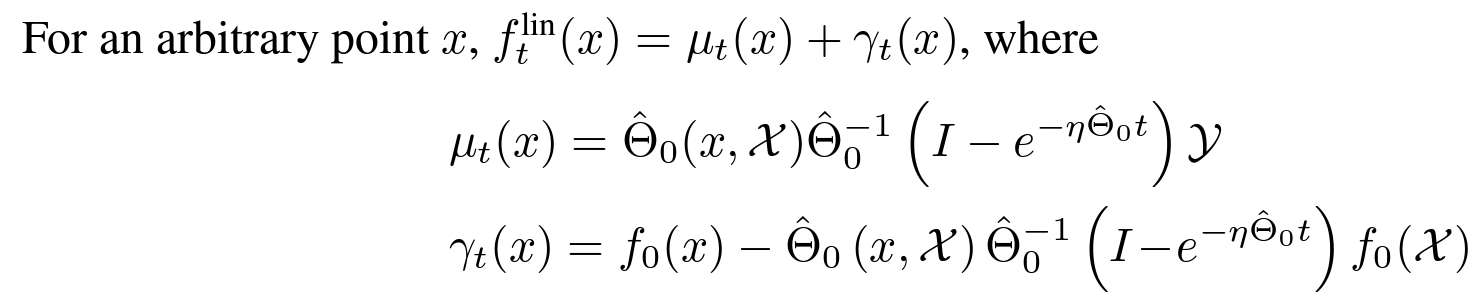
Finite wide networks
More importantly, they provided new approximation bounds for the predictions of the finite neural network and the linear-ized version:
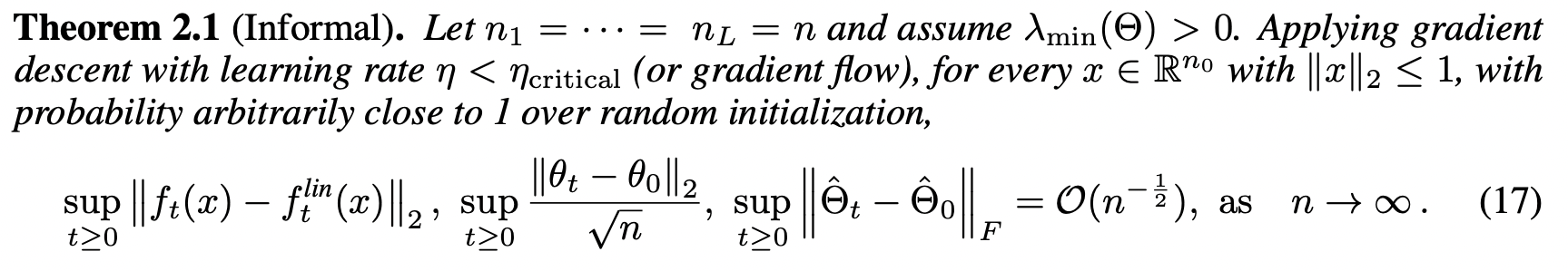
2. Applications of the Neural Tangent Kernel
NTK Applications
-
NTK Has enabled lots of theoretical insights into deep NNs:
- Studying the geometry of the loss landscape of NNs (Fort et al. 2020)
- Prediction and analyses of the uncertainty of a NN’s predictions (He et al. 2020, Adlam et al. 2020)
-
NTK Has been impactful in diverse practical settings:
- Predicting the trainability and generalization capabilities of a NN (Xiao et al. 2018 and 2020)
- Neural Architecture Search (Park et a. 2020, Chen et al. 2021)
NTK Applications
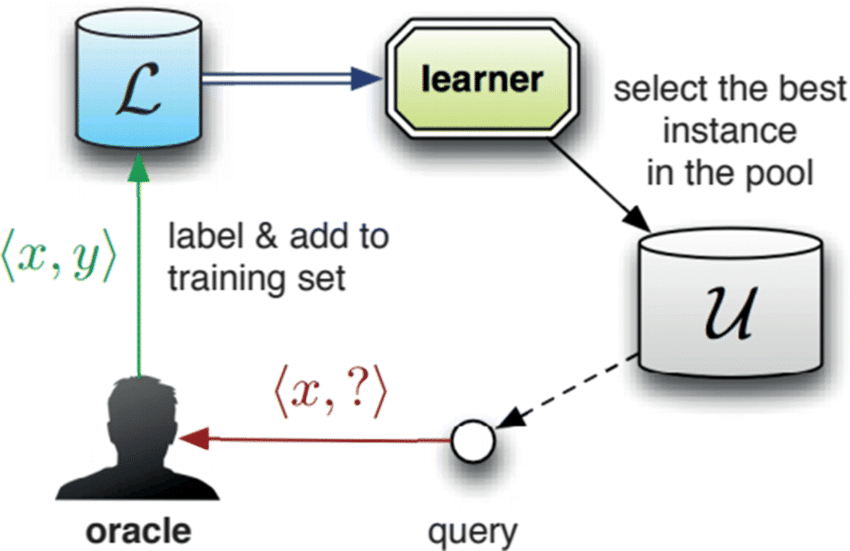
- We used NTK in pool-based active learning to enable "look-ahead" deep active learning
- Main idea: Approximate the behaviour of model after adding a new datapoint using a linear-ized version!
NTK Applications
NTK Applications
f_{\mathcal{L}^+}(x)
\approx f^\textit{lin}_{\mathcal{L}^+}(x)
=
f_\mathcal{L}(x) + \Theta_{\mathcal{L}}(x, \mathcal{X}^+){\Theta_{\mathcal{L}}(\mathcal{X}^+, \mathcal{X}^+)}^{-1} \left (\mathcal{Y}^+ - f_\mathcal{L}(\mathcal{X}^+) \right )
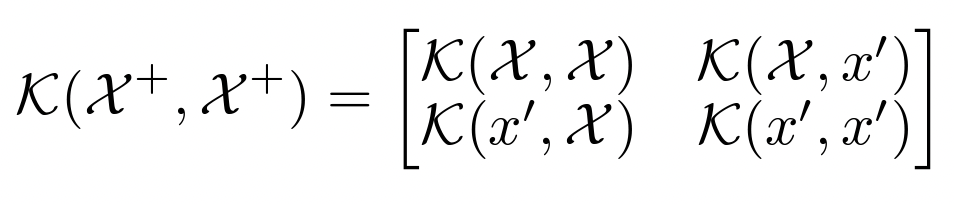
3. Approximating the Neural Tangent Kernel
NTK Computational Cost
-
Is, however, notoriously expensive to compute :(
- Both in terms of computational complexity, and memory complexity!
- Computing the Full empirical NTK of ResNet18 on Cifar-10 requires over 1.8 terabytes of RAM !
-
Our recent work:
- An approximation to the NTK, dropping the O term from the above equations!
\underbrace{\Theta_f(X_1, X_2)}_{N_1 O \times N_2 O} = \underbrace{J_\theta f(X_1)}_{N_1 \times O \times P} \otimes \underbrace{{J_\theta f(X_2)}^\top}_{P \times O \times N_2}
An Approximation to the NTK
- For each NN, we define pNTK as follows:
- Computing this approximation requires less time and memory complexity (Yay!)
\mathcal{O}(O^2)
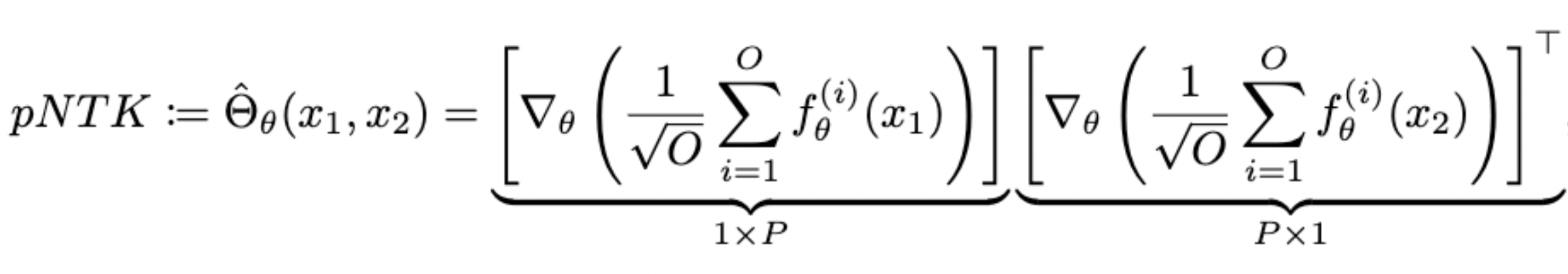
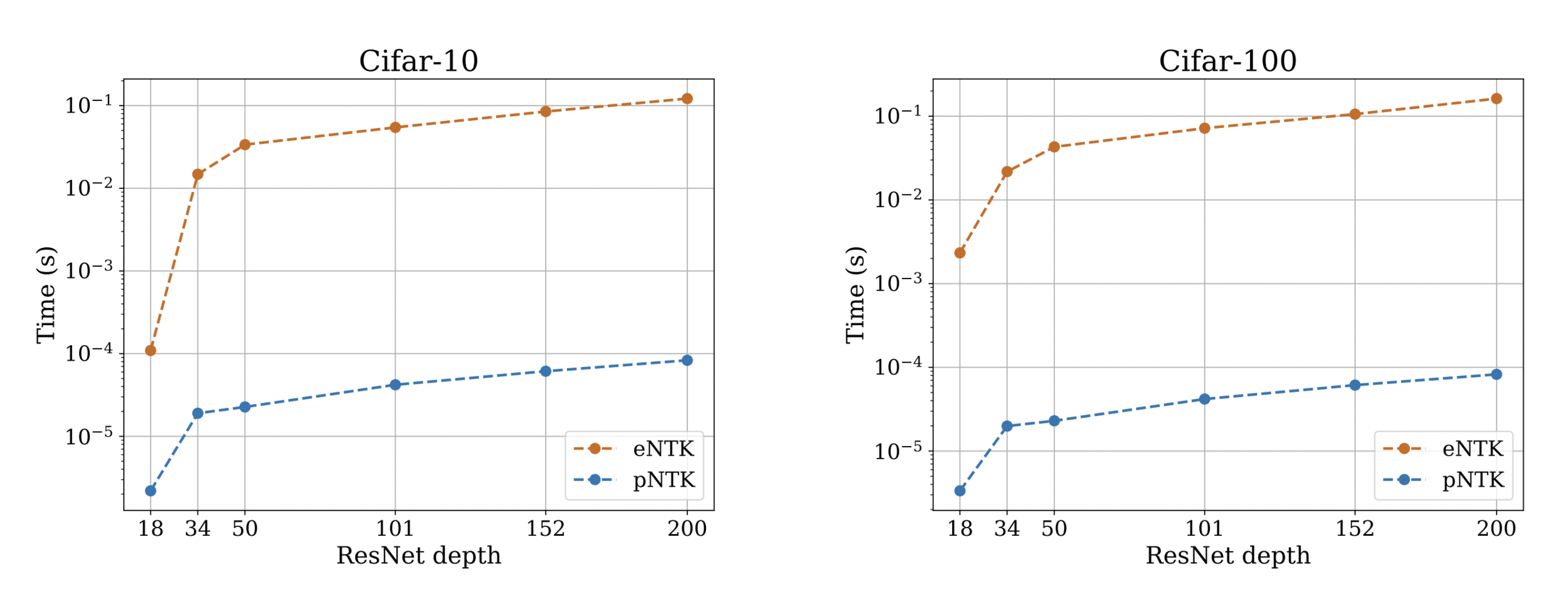
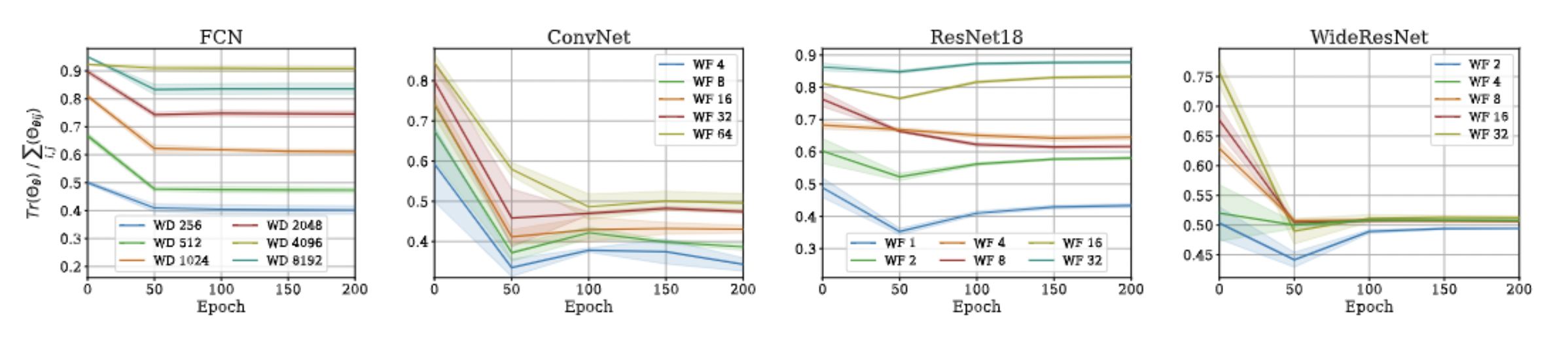
Approximation Quality: Frobenius Norm
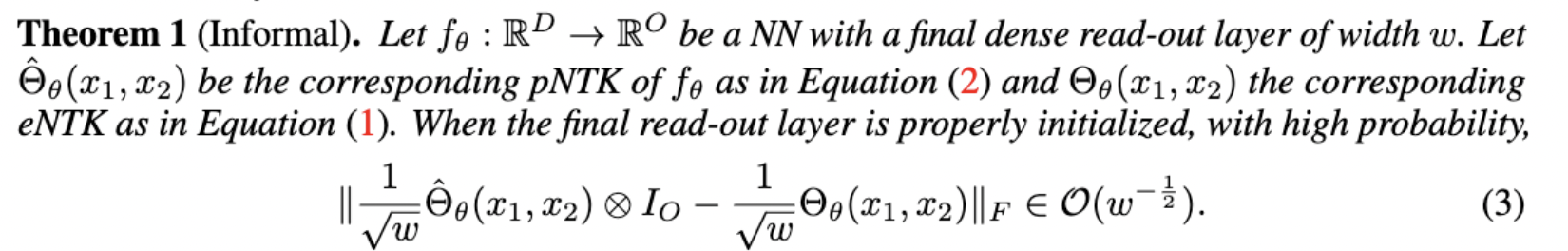
- Why?
- The diagonal elements of the difference matrix grow linearly with width
- The non-diagonal elements are constant with high probability
- Frobenius Norm of the difference matrix relatively converges to zero
Approximation Quality: Frobenius Norm
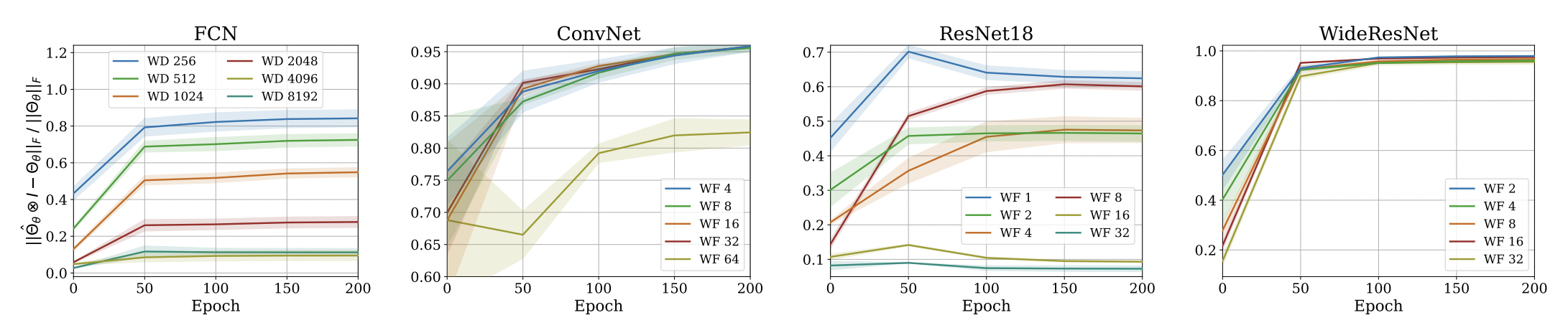
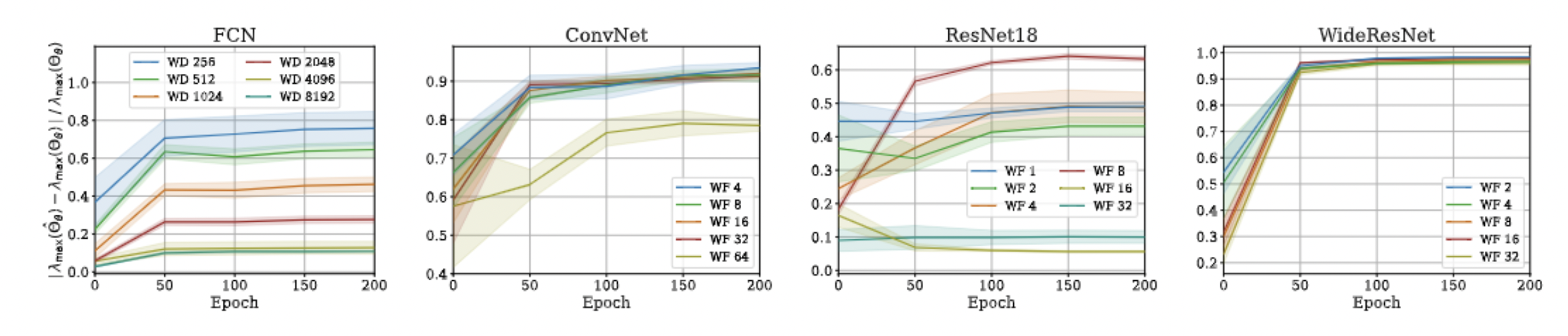
Approximation Quality: Eigen Spectrum
- Proof is very simple!
- Just a triangle inequality based on the previous result!
- Unfortunately, we could not come up with a similar bound for min eigenvalue and correspondingly the condition number, but empirical evaluations suggest that such a bound exists!
Approximation Quality: Eigen Spectrum
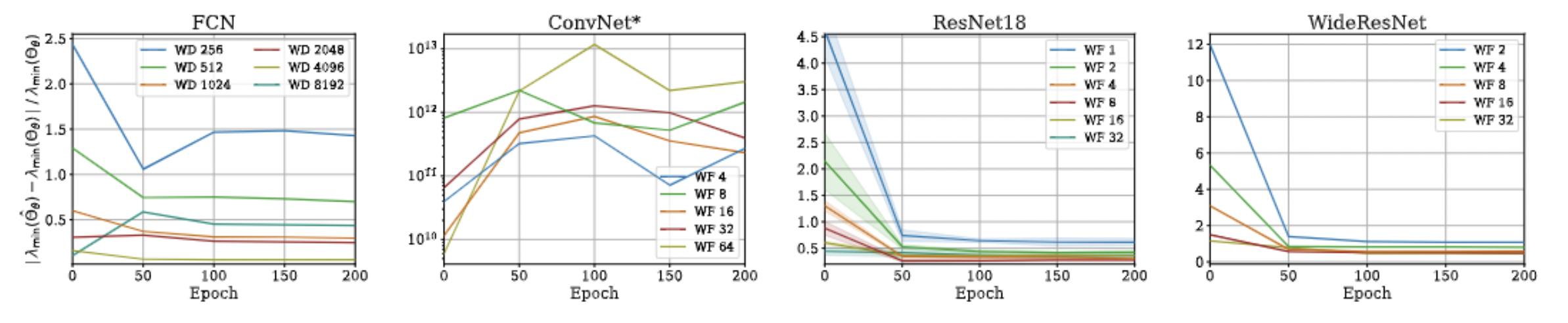
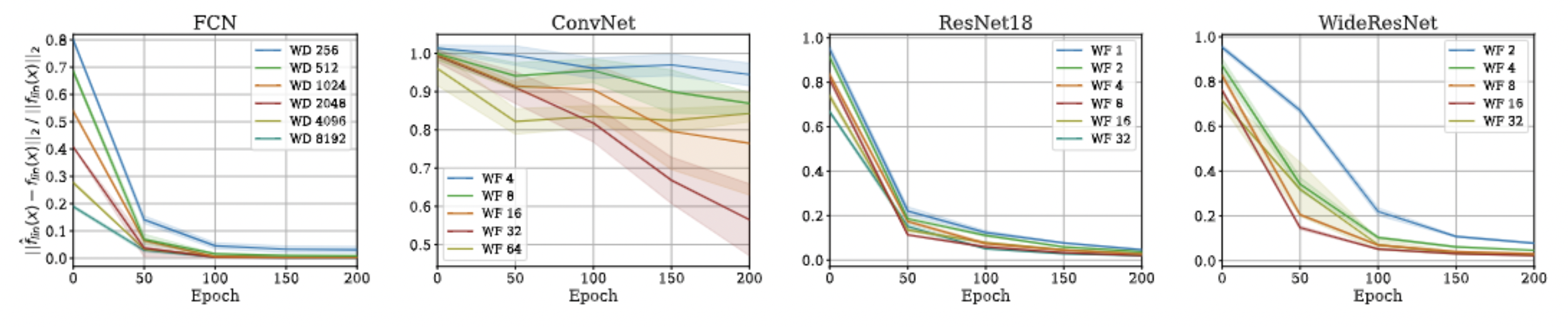
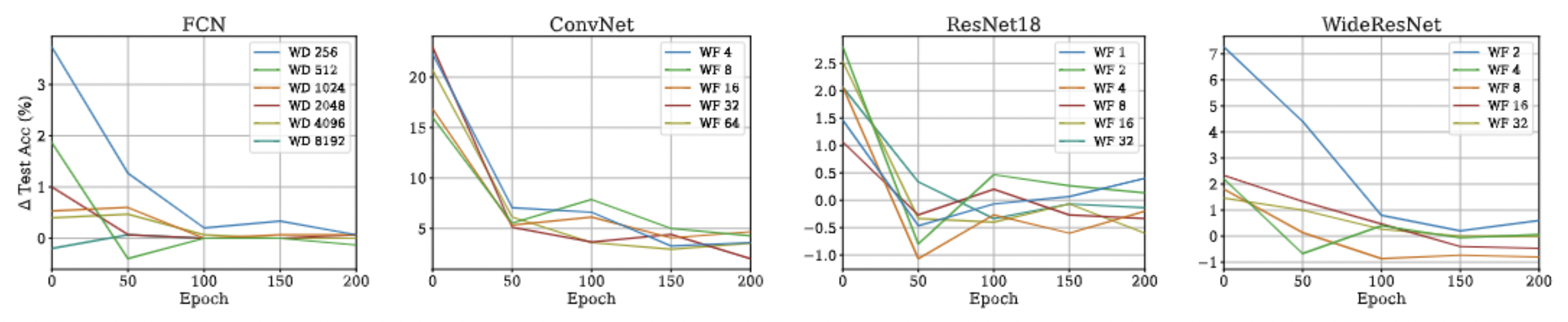
Approximation Quality: Kernel Regression
- Note: This approximation will not hold if there is any regularization (ridge) in the kernel regression! :(
- Note that we are not scaling the function values anymore!
Approximation Quality: Kernel Regression
Thank You! Questions?
Neural
By Amin Mohamadi
