Quantum Monte Carlo approaches for strongly correlated systems

Variational Monte Carlo

Stochastic multireference perturbation theory

Auxiliary field QMC

Outline

  • Sampling and the sign problem in AFQMC 
  • Reducing noise using selected CI wave functions 
  • Benchmark results
  • Jastrow symmetry projected states in VMC
  • Auxiliary field QMC
  • Variational MC
  • Use in projection QMC

A different take on projection QMC

Projection QMC methods:

e^{-\tau (\hat{H}-E_0)}|\psi\rangle = c_0|\Psi_0\rangle + c_1 e^{-\Delta E_1\tau}|\Psi_1\rangle+\dots
|\psi\rangle = c_0|\Psi_0\rangle + c_1|\Psi_1\rangle +\dots
  • Better \(|\psi\rangle\) approximates \(|\Psi_0\rangle\), faster the convergence with \(\tau\)
E(\tau)=\dfrac{\langle\psi_l|\hat{H}e^{-\tau \hat{H}}|\psi_r\rangle}{\langle\psi_l|e^{-\tau \hat{H}}|\psi_r\rangle}

Mixed energy estimator:

Trial states: Multi-Slater, CCSD, Jastrow, MPS, ...

  • Sign problem worsens exponentially with \(\tau\)

Sampling in AFQMC

\hat{H} = \hat{K} + \hat{V} = t_{pr} \hat{a}_{p}^{\dagger}\hat{a}_r + \frac{1}{2}v_{prqs}\hat{a}_{p}^{\dagger}\hat{a}_r\hat{a}_{q}^{\dagger}\hat{a}_{s}

Exponentiating \(\hat{H}\):  \([\hat{K}, \hat{V}] \neq 0\)

e^{-\tau\hat{H}}\approx\left(e^{-\frac{\tau}{N}\frac{\hat{K}}{2}}e^{-\frac{\tau}{N}\hat{V}}e^{-\frac{\tau}{N}\frac{\hat{K}}{2}}\right)^N
  • Exponentiating \(\hat{K}\):  orbital transformation
e^{t_{pr}\hat{a}_p^{\dagger}\hat{a}_r}|\phi\rangle=|\phi'\rangle

where \(|\phi\rangle\) and \(|\phi'\rangle\) are nonorthogonal determinants.

  • Exponentiating  \(\hat{V} = \frac{1}{2}\sum_{\gamma} \left(L^{\gamma}_{pr}\hat{a}_p^{\dagger}\hat{a}_r\right)^2\):
e^{-\frac{\hat{L}_{\gamma}^2}{2}} = \int \frac{dx_{\gamma}}{\sqrt{2\pi}}\ e^{\frac{-x_{\gamma}^2}{2}}e^{ix_{\gamma}\hat{L}_{\gamma}}

\(x_{\gamma}\): auxiliary field

Motta and Zhang (2017), 1711.02242

(Thouless, 1960)

(Stratonovich, 1957)

E(\tau) = \dfrac{\langle\psi_l|\hat{H}e^{-\tau \hat{H}}|\psi_r\rangle}{\langle\psi_l|e^{-\tau \hat{H}}|\psi_r\rangle} \approx \dfrac{\int\ dX p(X)\langle\psi_l|\hat{H}\hat{\mathcal{B}}(X)|\psi_r\rangle}{\int\ dX p(X)\langle\psi_l|\hat{\mathcal{B}}(X)|\psi_r\rangle}

Sample Gaussian auxiliary fields \(X\), propagate, and measure

E(\tau)\approx\dfrac{\sum_i\langle\psi_l|\hat{H}|\phi_i\rangle}{\sum_i\langle\psi_l|\phi_i\rangle}

CCSD as \(|\psi_r\rangle\): sampling Slater determinants from CCSD

|\psi_r\rangle = \exp\left(t_{ikjl}\hat{a}_i^{\dagger}\hat{a}_k\hat{a}_j^{\dagger}\hat{a}_l\right)\exp\left(t_{ik}\hat{a}_i^{\dagger}\hat{a}_k\right)|\phi_0\rangle

commuting ph excitations \(\rightarrow\) no Trotter error

\((\text{H}_2\text{O})_2\), (16e, 80o)

The sign problem

\text{Var}\left(\dfrac{\overline{N}}{\overline{D}}\right) \approx \dfrac{\text{Var}(\overline{N})}{\overline{D}^2} + \dfrac{\overline{N}^2\text{Var}(\overline{D})}{\overline{D}^4} - 2\dfrac{\overline{N}\text{Cov}(\overline{N},\overline{D})}{\overline{D}^3}
E(\tau)\approx\dfrac{\sum_i\langle\psi_l|\hat{H}|\phi_i\rangle}{\sum_i\langle\psi_l|\phi_i\rangle} = \dfrac{\overline{N}}{\overline{D}}

Contour shift:

e^{-\frac{y^2}{2}} = \int \frac{dx}{\sqrt{2\pi}}\ e^{\frac{-x^2}{2}+ixy}
x\rightarrow x+iy
x_{\gamma} \rightarrow x_{\gamma} + i \sqrt{\tau}\langle\hat{L}_{\gamma}\rangle

In AFQMC:

Baer, Head-Gordon, Neuhauser (1998)

Selected CI trial state as \(|\psi_l\rangle\)

Zero variance principle: If \(|\psi_l\rangle\) is the exact ground state, then \(N\) and \(D\) are perfectly correlated, \(\langle\psi_0|\hat{H}|\phi_i\rangle = E_0 \langle\psi_0|\phi_i\rangle\), and the energy estimator has zero variance. 

More accurate \(|\psi_l\rangle\ \rightarrow\ \) higher \(\text{Cov}(N, D)\)

E(\tau)\approx\dfrac{\sum_i\langle\psi_l|\hat{H}|\phi_i\rangle}{\sum_i\langle\psi_l|\phi_i\rangle} = \dfrac{\overline{N}}{\overline{D}}
\text{Var}\left(\dfrac{\overline{N}}{\overline{D}}\right) \approx \dfrac{\text{Var}(\overline{N})}{\overline{D}^2} + \dfrac{\overline{N}^2\text{Var}(\overline{D})}{\overline{D}^4} - 2\dfrac{\overline{N}\text{Cov}(\overline{N},\overline{D})}{\overline{D}^3}

\((\text{H}_2\text{O})_2\), (16e, 80o)

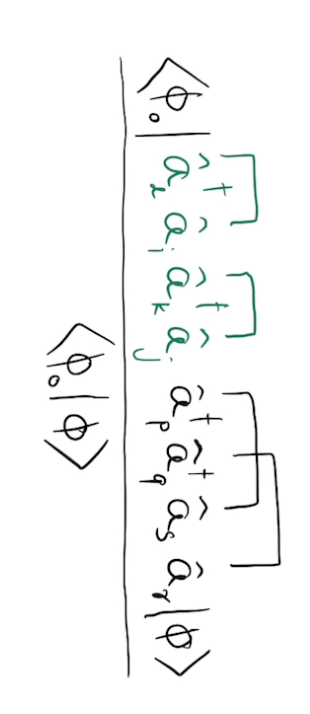
Selected CI local energy algorithm

E_L[\phi]=\dfrac{\langle\psi_l|\hat{H}|\phi\rangle}{\langle\psi_l|\phi\rangle},\ \text{two-body part: }\ L^{\gamma}_{pr}L^{\gamma}_{qs}\dfrac{\langle\psi_l|\hat{a}_p^{\dagger}\hat{a}_q^{\dagger}\hat{a}_s\hat{a}_r|\phi\rangle}{\langle\psi_l|\phi\rangle}

If \(|\psi_l\rangle\) is a Slater determinant: \(|\psi_l\rangle = |\phi_0\rangle\)

O(N^4)

If \(|\psi_l\rangle\) is a selected CI wave function: \(|\psi_l\rangle = \sum_i^{N_d} c_i |\phi_i\rangle\)

Naive way: calculating local energy of each Slater determinant as above costs \(O(N_dN^4)\)

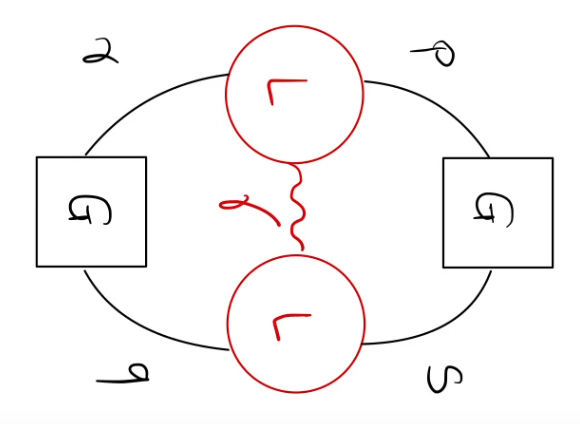
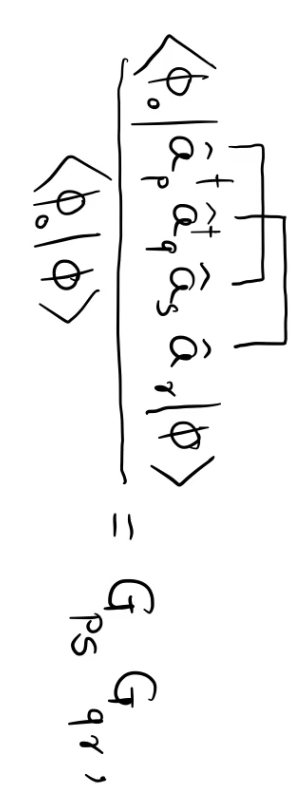
One of the terms:

Consider doubly excited determinants:  \(c_{jkil} \hat{a}_j^{\dagger} \hat{a}_k \hat{a}_i^{\dagger} \hat{a}_l |\phi_0\rangle\)

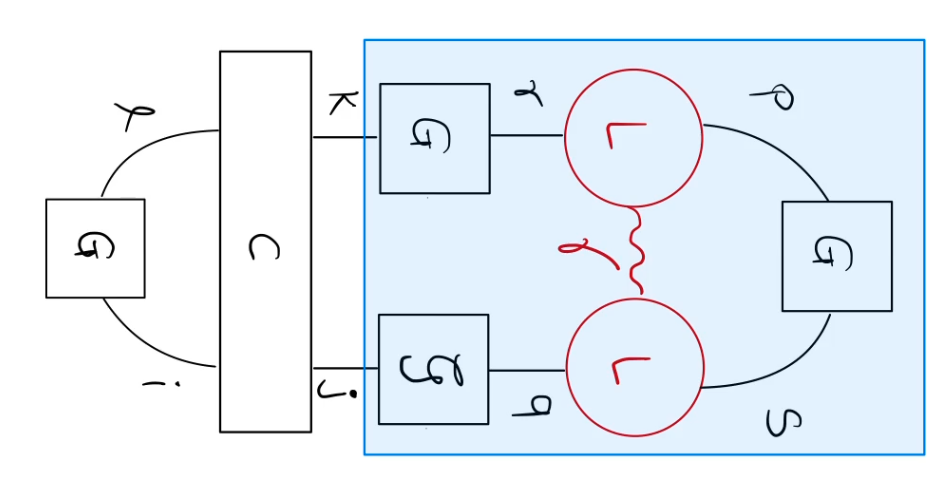
store intermediate

Overall scaling: \(O(N^4 + N_dN)\)

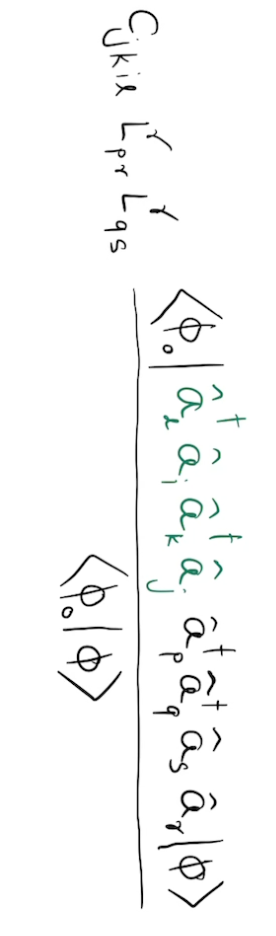
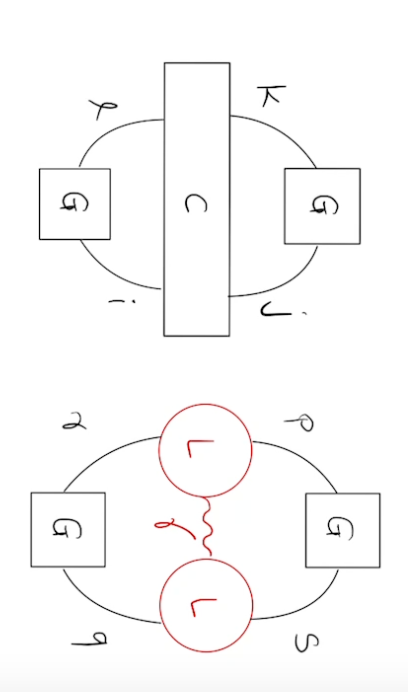
factorizable term

\((\text{H}_2\text{O})_2\), (16e, 80o)

Cyclobutadiene automerization barrier

Method DZ (20e, 72o) TZ (20e, 172o)
CCSD(T)   15.8 18.2
CCSDT 7.6 10.6
TCCSD (12,12) - 9.2
MRCI+Q - 9.2
fp-AFQMC 8.4(4) 10.2(4)

kcal/mol

\([\text{Cu}_2\text{O}_2]^{2+}\) isomerization

kcal/mol

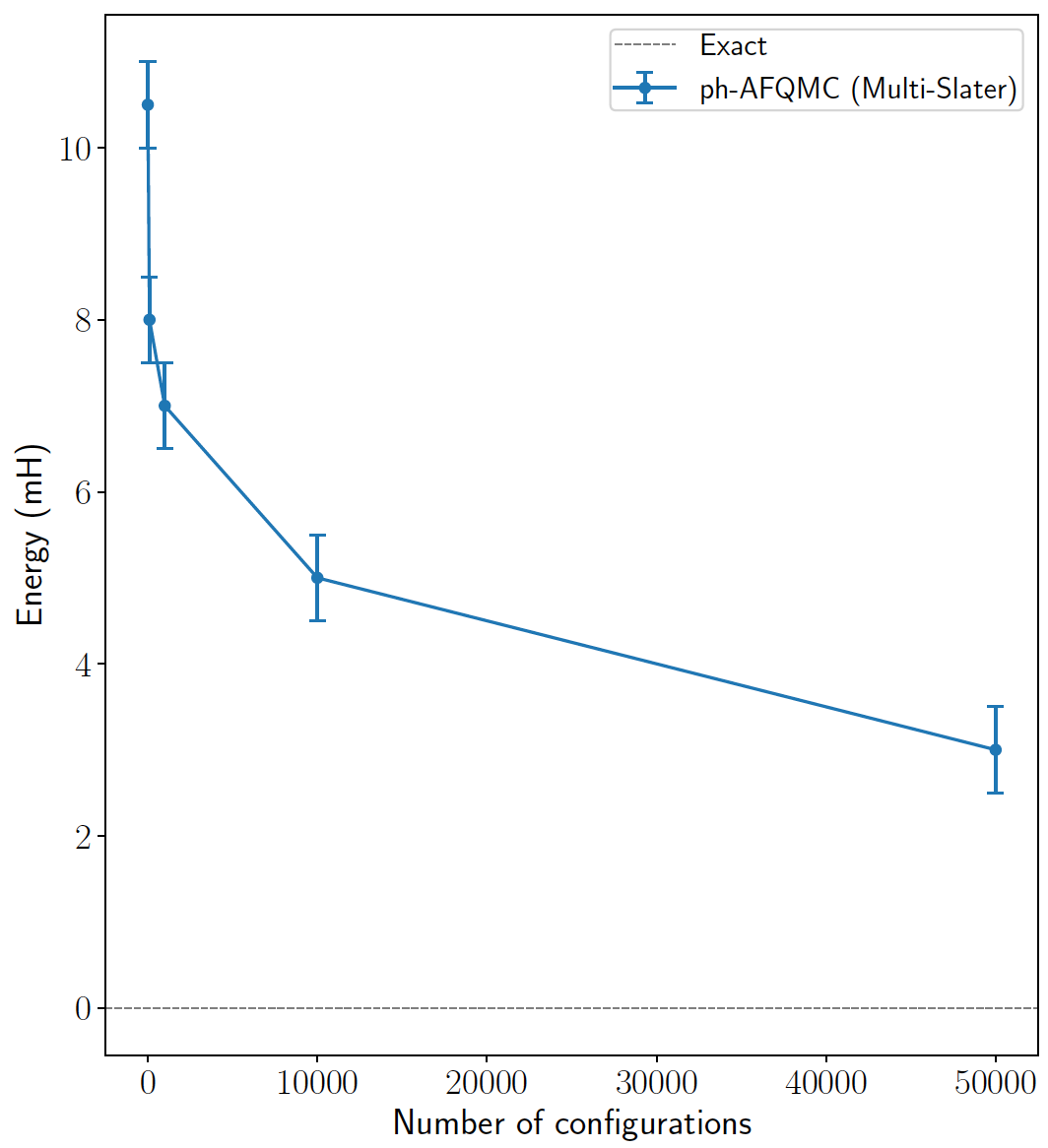
Converging phaseless bias in ph-AFQMC

FeO (22e, 76o)

Symmetry projection in VMC

Symmetry breaking \(\rightarrow\) more variational freedom

Break the symmetry under a projector, to retain good quantum numbers

|\psi\rangle=\hat{P}|\phi\rangle

Projection in VMC by restricting random walk to the symmetry sector

Symmetries: spin, number, complex conjugation, ...

Example: complex conjugation in \(\text{H}_2\) near dissociation

|\text{RHF}\rangle = (a_{1\uparrow}^{\dagger}+a_{2\uparrow}^{\dagger})(a_{1\downarrow}^{\dagger}+a_{2\downarrow}^{\dagger})|0\rangle = (a_{1\uparrow}^{\dagger}a_{1\downarrow}^{\dagger}+a_{1\uparrow}^{\dagger}a_{2\downarrow}^{\dagger}+a_{2\uparrow}^{\dagger}a_{1\downarrow}^{\dagger}+a_{2\uparrow}^{\dagger}a_{2\downarrow}^{\dagger})|0\rangle
|\text{cRHF}\rangle = (e^{i\pi/4}a_{1\uparrow}^{\dagger}+e^{-i\pi/4}a_{2\uparrow}^{\dagger})(e^{i\pi/4}a_{1\downarrow}^{\dagger}+e^{-i\pi/4}a_{2\downarrow}^{\dagger})|0\rangle\\ \quad = (ia_{1\uparrow}^{\dagger}a_{1\downarrow}^{\dagger}+a_{1\uparrow}^{\dagger}a_{2\downarrow}^{\dagger}+a_{2\uparrow}^{\dagger}a_{1\downarrow}^{\dagger}-ia_{2\uparrow}^{\dagger}a_{2\downarrow}^{\dagger})|0\rangle
\hat{K}|\text{cRHF}\rangle = (a_{1\uparrow}^{\dagger}a_{2\downarrow}^{\dagger}+a_{2\uparrow}^{\dagger}a_{1\downarrow}^{\dagger})|0\rangle
\hat{P}\hat{\mathcal{J}}|\psi\rangle = \hat{P}\exp\left(\sum_{p\sigma,q\gamma} v_{p\sigma,q\gamma}\hat{n}_{p\sigma}\hat{n}_{q\gamma}\right)|\psi\rangle

Jastrow symmetry projected state:

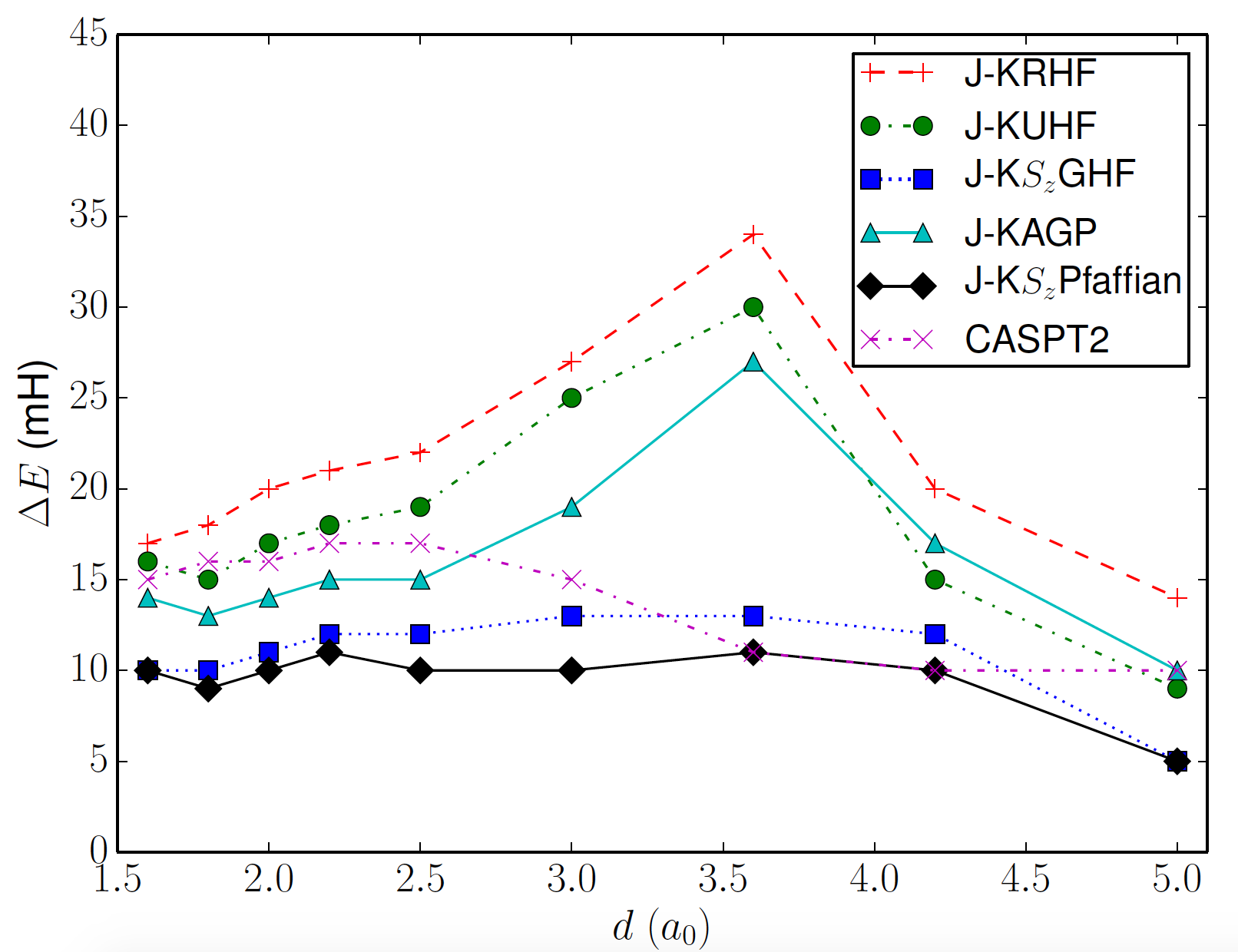
\(\text{N}_2\)

d (Bohr) Exact (DMRG) Jastrow-KS_zPfaffian Green's function MC
1.6 -0.5344 -0.5337 -0.5342
1.8 -0.5408 -0.5400 -0.5406
2.5 -0.5187 -0.5180 -0.5185

H\( _{50} \) linear chain (50e, 50o)

U Benchmark energy Jastrow-
KS_zGHF		 Green's function MC
2 -1.1962 -1.1920 -1.1939
4 -0.8620 -0.8566 -0.8598
8 -0.5237 -0.5183 -0.5221

2D Hubbard: 98 sites (half filling)

Hartree/particle

Future directions

  • Properties and excited states
  • Importance sampling and constraints in AFQMC, hybrid MD-MC
  • Variational CCSD, other wave functions like MPS, Jastrow in AFQMC
  • Spin liquid states in iridates using VMC

Thank you!

afqmc_vmc

By Ankit Mahajan

afqmc_vmc

  • 280

More from Ankit Mahajan