Jastrow multi-Slater electronic wave functions
Challenging electronic structure problems
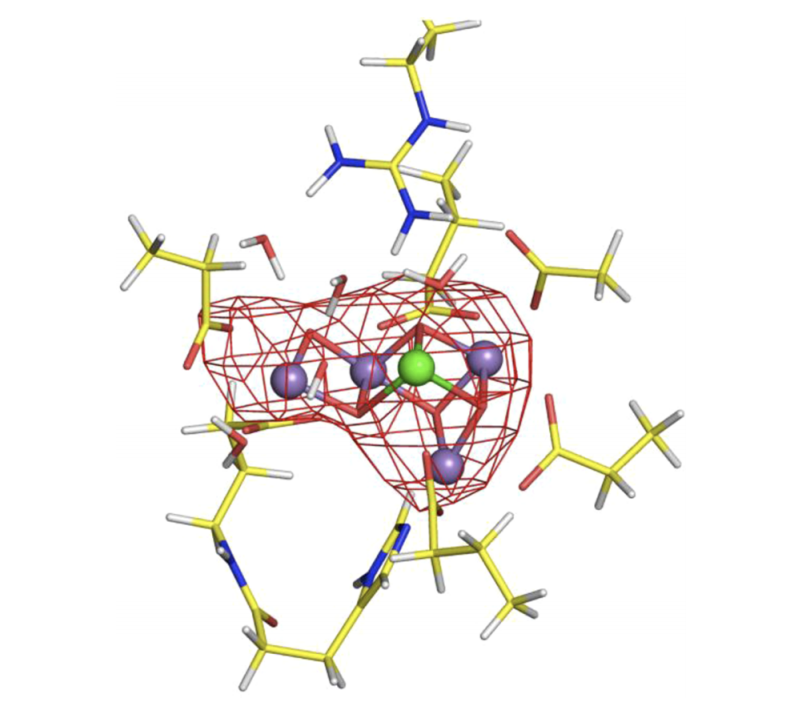
oxygen evolving complex (photosynthesis)
Cluster models of metalloenzymes
$$[\text{Mn}_4\text{CaO}_5]$$
$$[\text{Cu}_2\text{O}_2]$$
tyrosinase
(melanin production)
Example: \( [\text{Cu}_2\text{O}_2]^{2+} \) isomerization
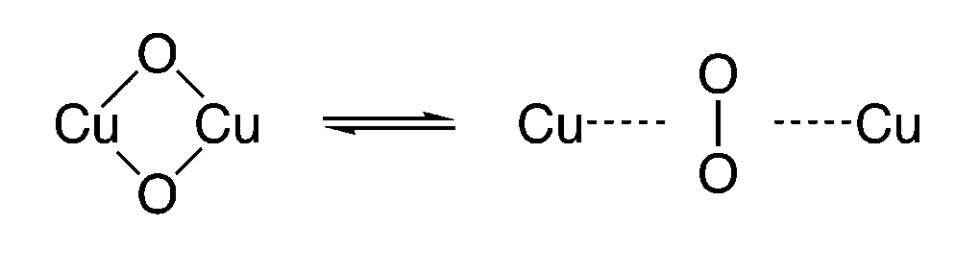
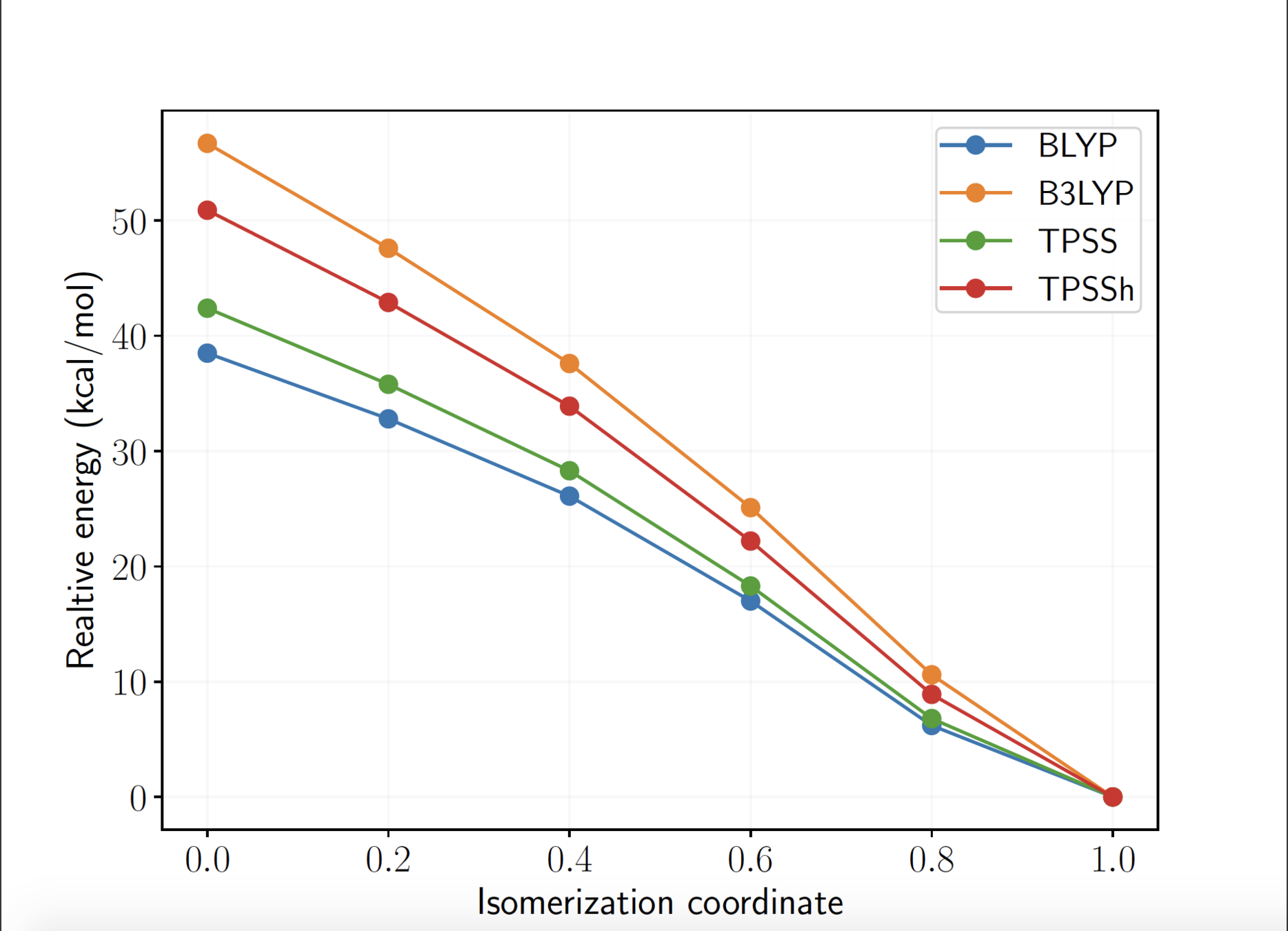
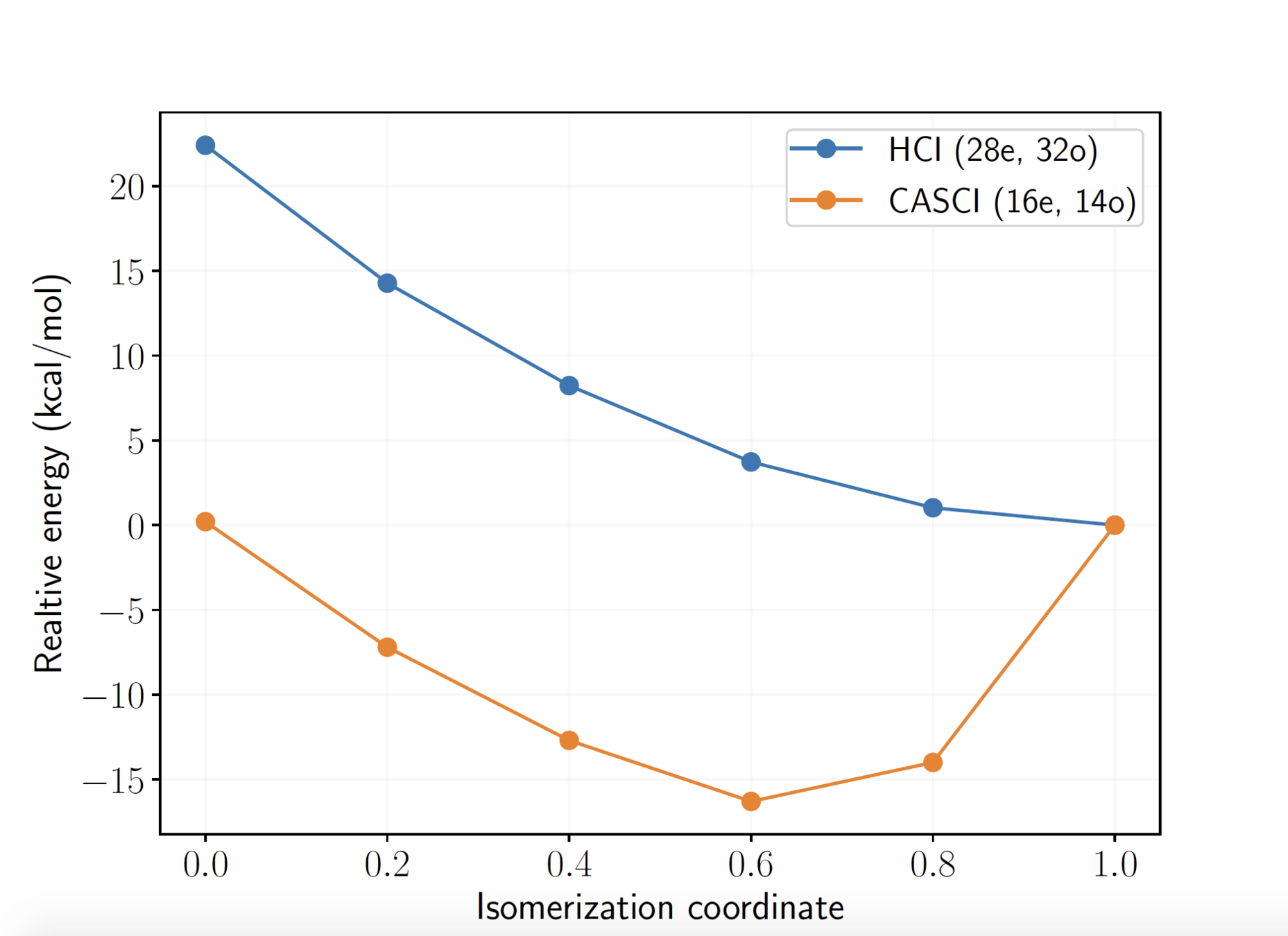
DFT: large differences in relative energies depending on the functional
Active space wave functions: (28e, 32o) includes Cu 3d, 4d, and O 2p, 3p orbitals, Hilbert space dimension: \(10^{17}\)!
Cramer et al. J. Phys. Chem. A 2006, 110, 1991-2004
arXiv:2008.00220
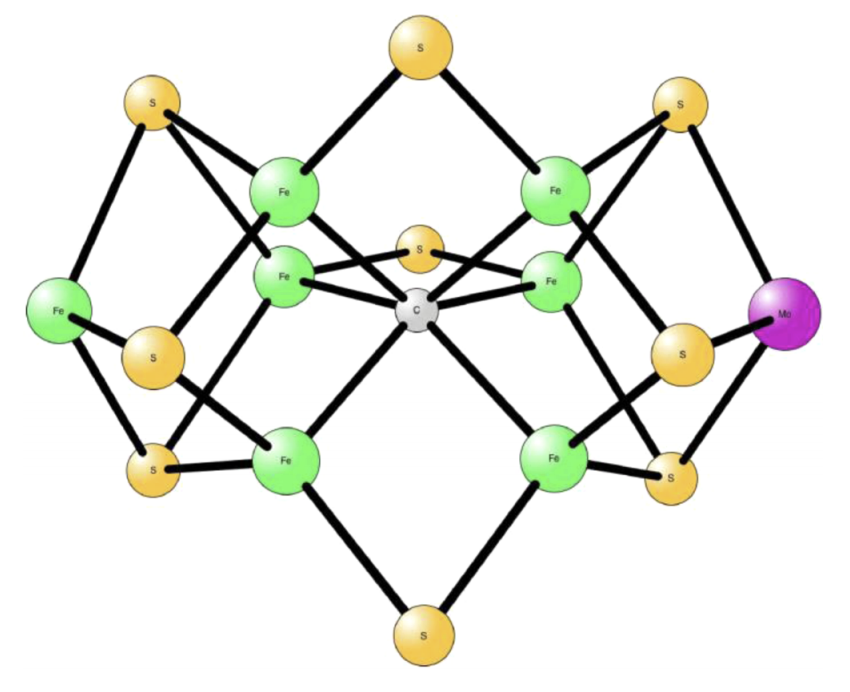
Nitrogenase FeMo cofactor
7 iron atoms, 1 molybdenum atom
Local and canonical descriptions
\hat{H} = -\sum_{\langle ij\rangle,\sigma}(\hat{a}_{i\sigma}^{\dagger}\hat{a}_{j\sigma}+\hat{a}_{j\sigma}^{\dagger}\hat{a}_{i\sigma}) + U\sum_i\hat{n}_{i\uparrow}\hat{n}_{i\downarrow}
Hubbard:
hopping (kinetic energy)
onsite e-e repulsion
Ground state of half-filled 1-D 6 site model: U = 1
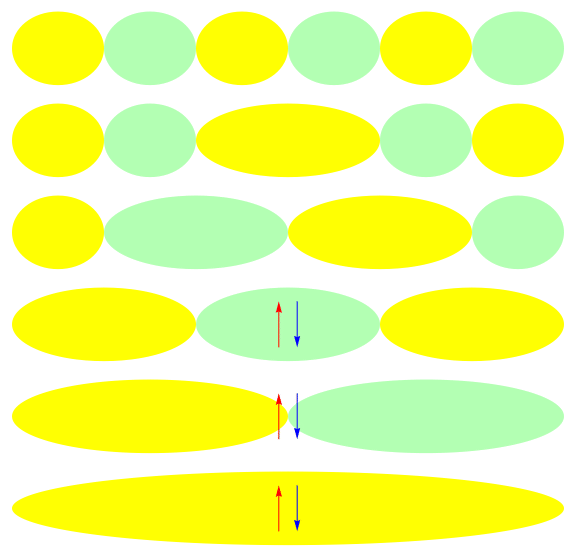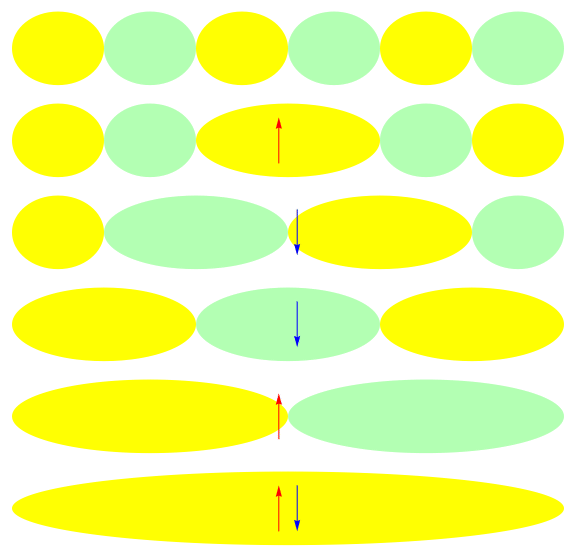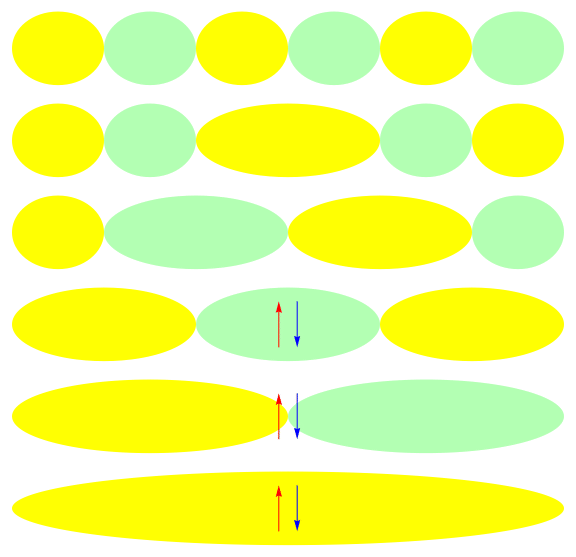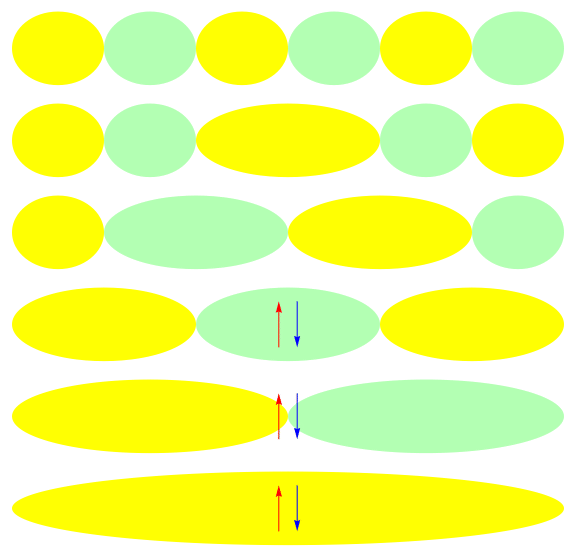
\( x\)
\(E\)
Efficient description using delocalized canonical orbital configurations:
|\psi\rangle= |\phi_0\rangle + \sum_i c_i\hat{E}_i|\phi_0\rangle
Hartree-Fock reference
particle hole excitations
Ground state of half-filled 1-D 6 site model: U = 10
Local and canonical descriptions
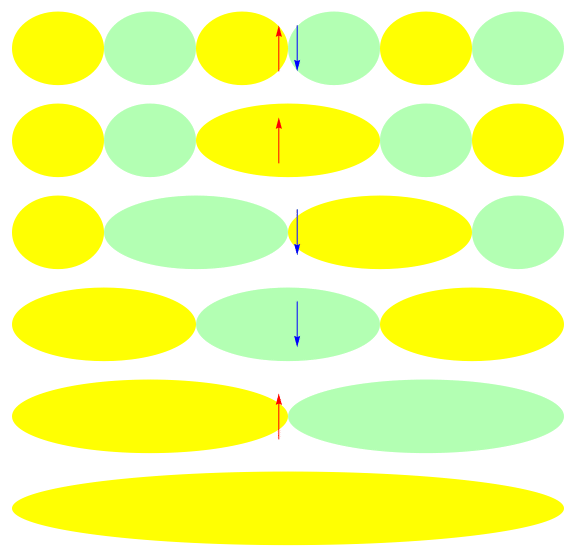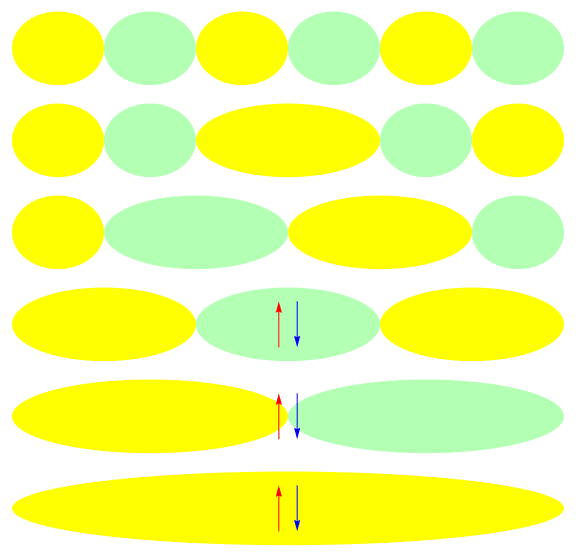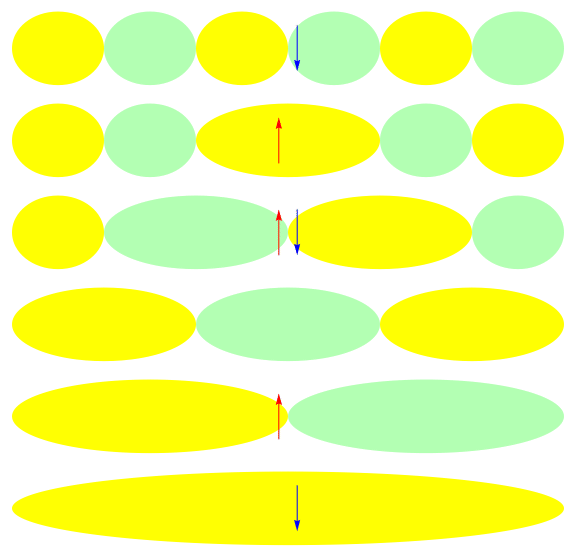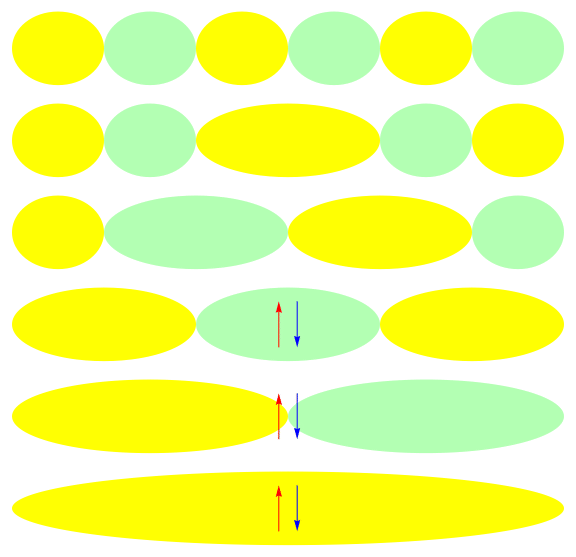
Efficient description with a Jastrow factor using local orbitals:
|\psi\rangle = \exp\left(\sum J_{ij}\hat{n}_i\hat{n}_j\right)|\phi_0\rangle
Jastrow
HF ref.
Correlation by penalizing local charge fluctuations
Combining Jastrow with multi-Slater: Jastrow encodes strong interactions, while multi-Slater captures weak and more general interactions, like exchange
|\psi\rangle = \exp\left(\sum J_{ij}\hat{n}_i\hat{n}_j\right) \sum_i c_i|\phi_i\rangle
|\phi_i\rangle = \prod \hat{C}_t^{\dagger}\hat{C}_p|\phi_0\rangle
Variational principle
Energy of any "valid" wave function is an upper bound for the ground state energy:
E[\psi]=\dfrac{\langle\psi|\hat{H}|\psi\rangle}{\langle\psi|\psi\rangle}\geq E_0
To find an approximation to the ground state wave function:
- Start with a wave function parametrization: Jastrow multi-Slater
- Calculate energy: we use variational Monte Carlo (VMC) to perform a random walk in the space of local orbital electronic configurations:
E[\psi] = \langle E_L\rangle,\quad E_L[n] = \dfrac{\langle n|\hat{H}|\psi\rangle}{\langle n|\psi\rangle}
- Vary parameters to minimze energy: difficult nonlinear optimization
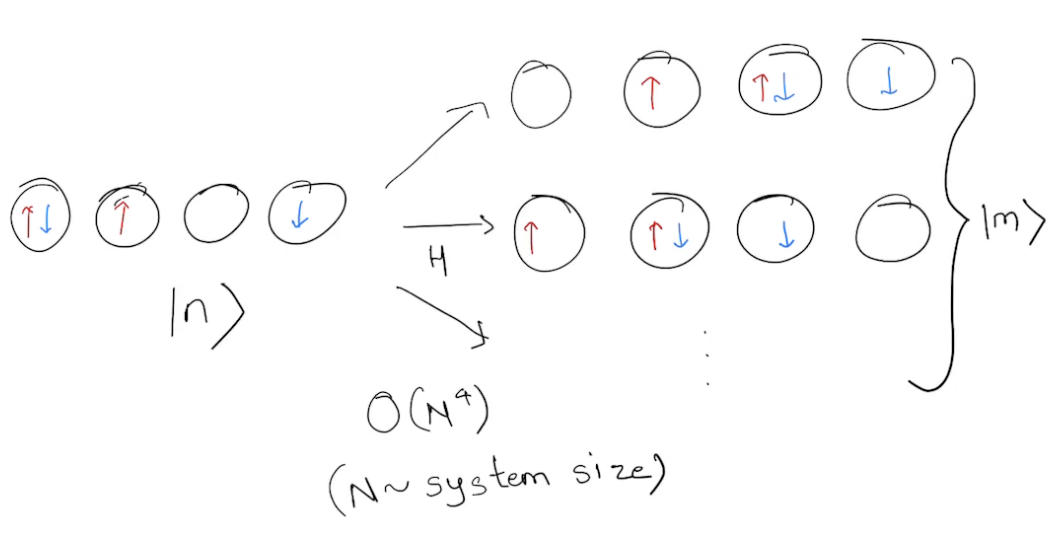
local energy of walker \(|n\rangle\)
Local energy of Jastrow multi-Slater
The local energy is given by
\dfrac{\langle n|\hat{H}|\psi\rangle}{\langle n|\psi\rangle}=\sum_m\langle n|\hat{H}\hat{\mathcal{J}}|m\rangle\sum_ic_i\dfrac{\langle m|\phi_i\rangle}{\langle n|\psi\rangle},
\hat{H} = \sum h_{ia}\hat{L}_a^{\dagger}\hat{L}_{i}+\sum v_{ijab}\hat{L}^{\dagger}_a\hat{L}_b^{\dagger}\hat{L}_j\hat{L}_i
Sum of \(N_c\) such terms for each \(|m\rangle\). Since there are \(O(N^4)\) \(|m\rangle\), this is expensive.
\langle m|\phi_i\rangle = \langle n|\prod \hat{L}_i^{\dagger}\hat{L}_a\prod \hat{C}_t^{\dagger}\hat{C}_p|\phi_0\rangle
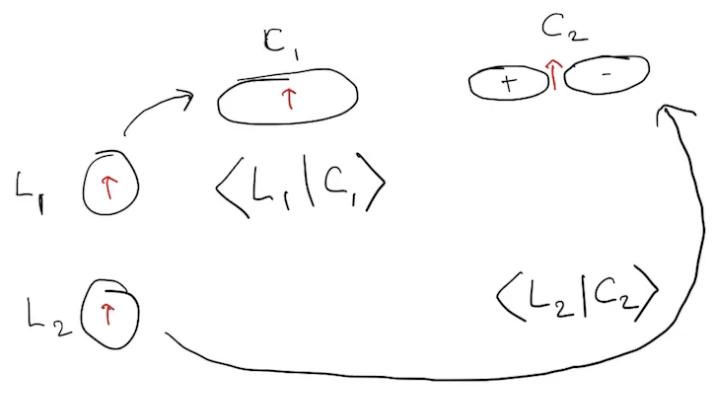
What is the overlap between a local configuration and a canonical one?
\(\hat{L}\): local, \(\hat{C}\): canonical
Overlaps are determinants
\(\langle L_1L_2|C_1C_2\rangle =\) Amplitude of \(|L_1L_2\rangle\rightarrow|C_1C_1\rangle\)
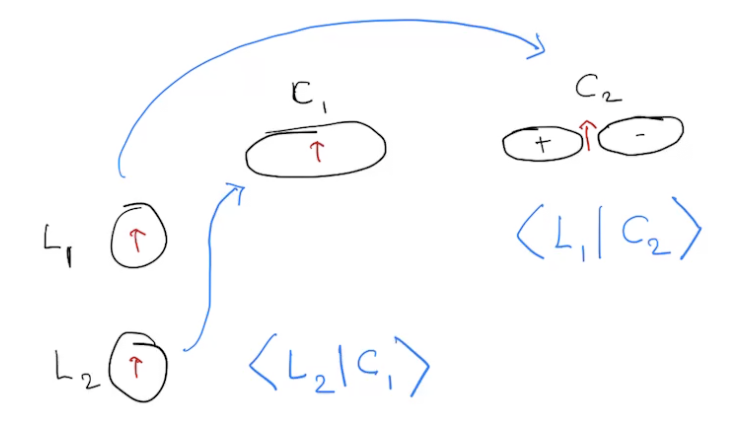
Two ways to accomplish this:
or
\(L_1\rightarrow C_1\) and \(L_2\rightarrow C_2\): \( \langle L_1|C_1\rangle \times \langle L_2|C_2\rangle\)
\(L_1\rightarrow C_2\) and \(L_2\rightarrow C_1\): \( \langle L_1|C_2\rangle \times \langle L_2|C_1\rangle\)
\langle L_1L_2|C_1C_2\rangle = \langle L_1|C_1\rangle
\langle L_2|C_2\rangle -
\langle L_1|C_2\rangle
\langle L_2|C_1\rangle = \det\begin{pmatrix}
\langle L_1|C_1\rangle & \langle L_1|C_2\rangle\\
\langle L_2|C_1\rangle & \langle L_2|C_2\rangle\\
\end{pmatrix}
fermion antisymmetry
Cost of calculating \(N\times N\) determinant: \(O(N^3)\)
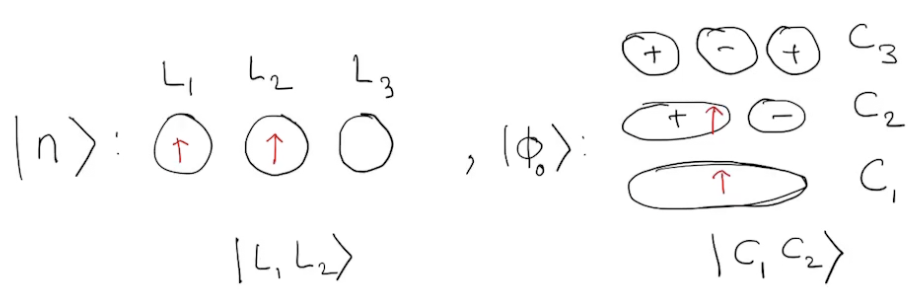
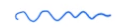
Generalized Wick's theorem
\dfrac{\langle n|\hat{L}_i^{\dagger}\hat{L}_a|\phi_0\rangle}{\langle n|\phi_0\rangle}=G^L_{ai},
Green's function,
involves calculating inverse (\(O(N^3)\))
\dfrac{\langle n|\hat{L}_i^{\dagger}\hat{L}_a\hat{L}^{\dagger}_j\hat{L}_b|\phi_0\rangle}{\langle n|\phi_0\rangle}=G^L_{ai}G^L_{bj}-G^L_{aj}G^L_{bi}
\(2\times2\) determinant
ratio of \(N\times N\) determinants
By storing the Green's functions, calculation of large determinants can be avoided.
\dfrac{\langle n|\hat{C}_t^{\dagger}\hat{C}_p|\phi_0\rangle}{\langle n|\phi_0\rangle}=G^C_{pt},
\dfrac{\langle n|\hat{L}_i^{\dagger}\hat{C}_p|\phi_0\rangle}{\langle n|\phi_0\rangle}=G'_{pi},
\dfrac{\langle n|\hat{L}_a\hat{C}_t^{\dagger}|\phi_0\rangle}{\langle n|\phi_0\rangle}=G''_{at},
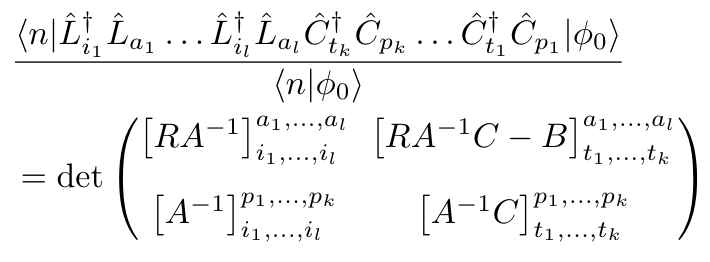
general formula
Using intermediates to speed up sums
With these Green's functions, local energy can be calculated at cost \(O(N^4N_c)\), which is still very expensive when \(N_c > 10^3\).
There's a pattern in the contribution of a configuration to the local energy:
\dfrac{\langle n|\hat{H}_2|\phi_i\rangle}{\langle n|\phi_0\rangle} =
the bottom right block of the determinants is the same
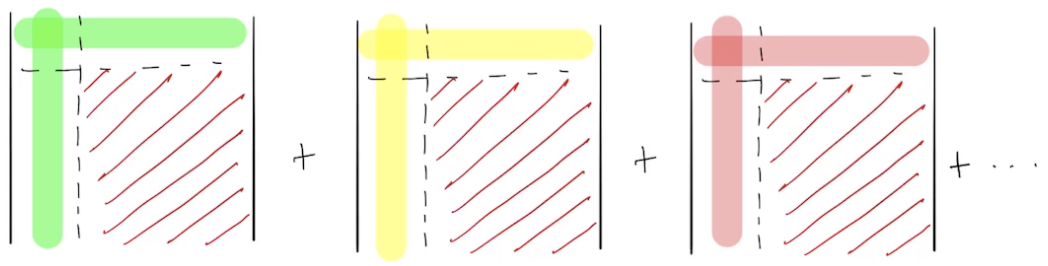
Using this observation, local energy calculation can be performed at cost \(O(N^5+N_c)\), by storing some intermediates.
(This concept is analogous to when performing the product of three matrices \(A\times B\times C\), one stores \(A\times B\) or \(B\times C\) as an intermediate)
Polyacetylene calculations
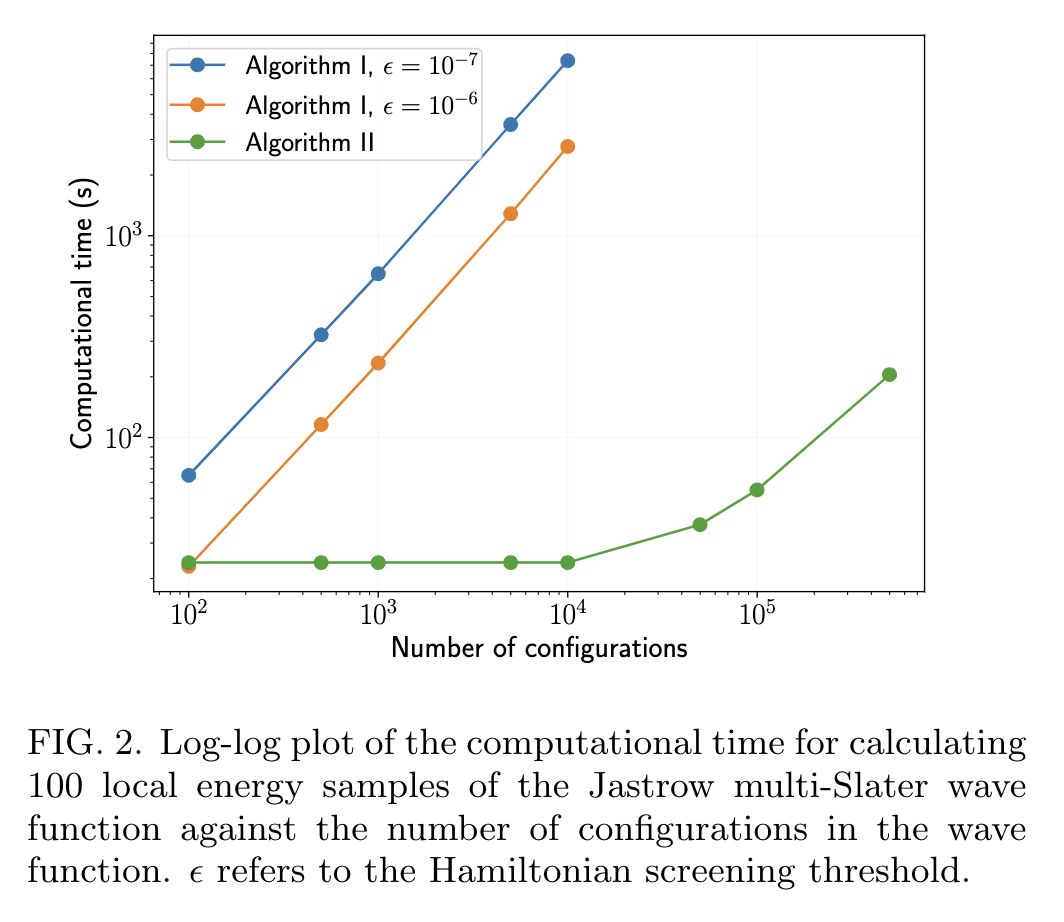
\(n = 28\): active space of \(\pi\) orbitals (28e, 28o)
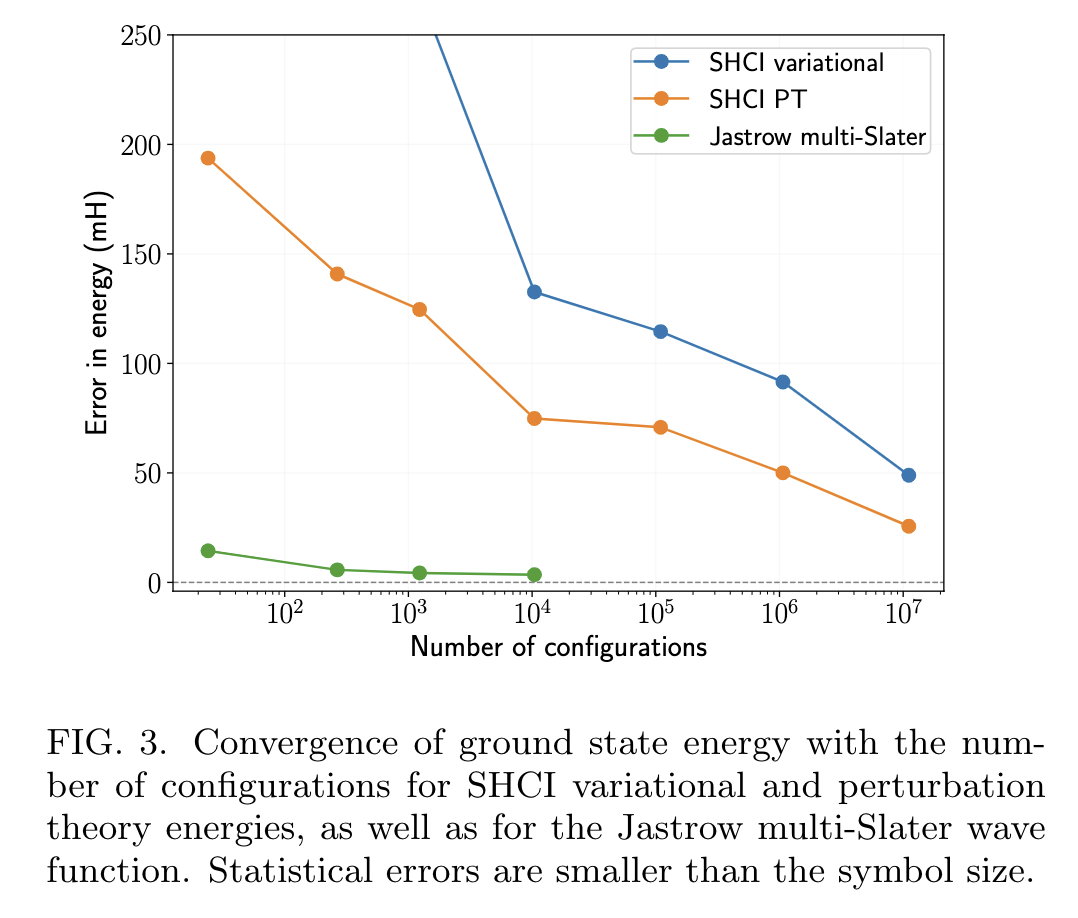
arXiv:2008.06477
Challenges
- Dynamic correlation: effect of non-valence virtual orbitals. Important for quantitative accuracy
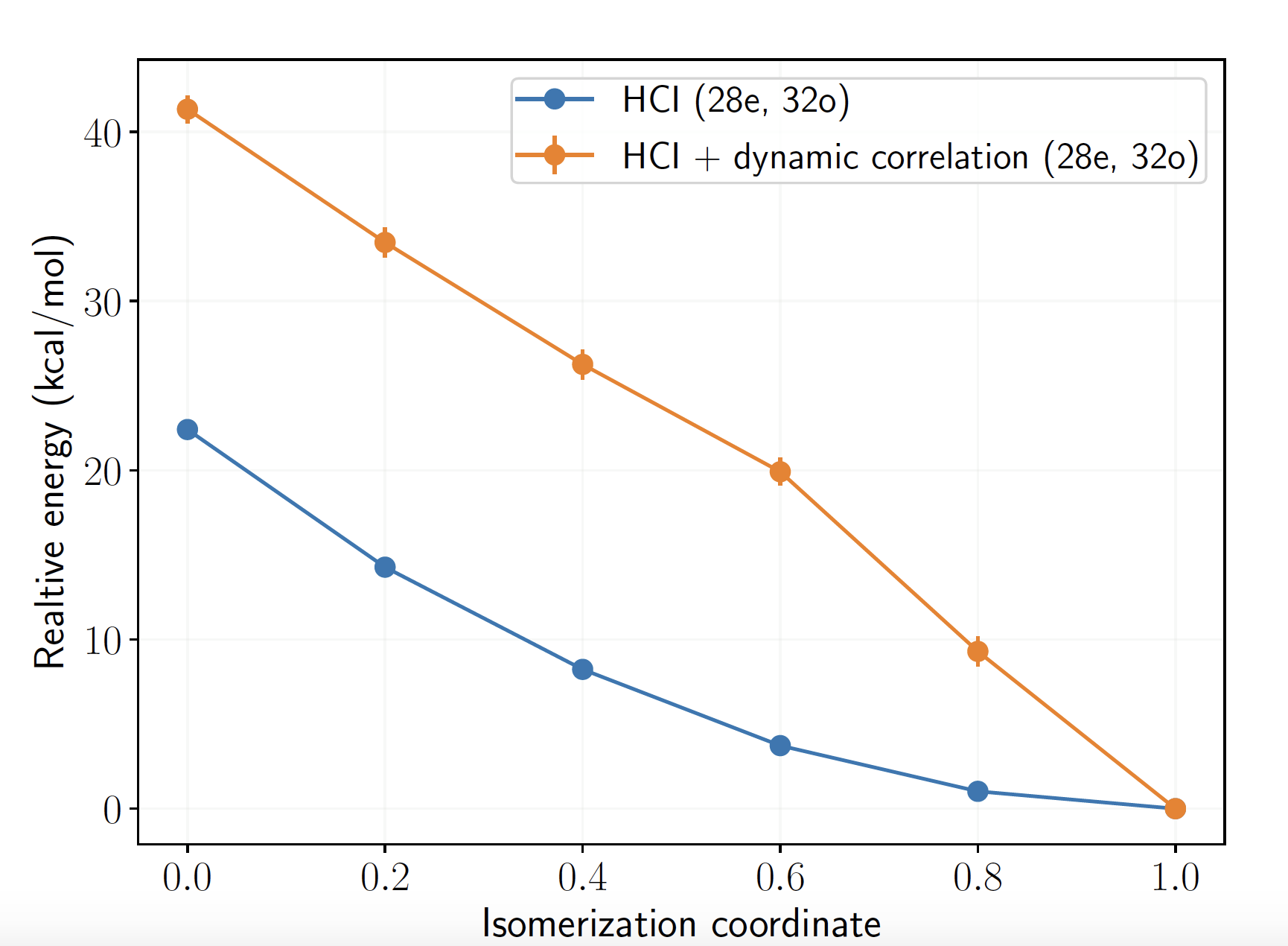
[\(\text{Cu}_2\text{O}_2\)]
arXiv:2008.00220
- VMC optimization limits the number of configurations that can be feasibly used
Both of these could be potentially tackled by using projection Monte Carlo
Auxiliary field quantum Monte Carlo
Imaginary time evolution (projection)
\hat{H} = \sum h_{ia}\hat{c}_a^{\dagger}\hat{c}_{i}+\sum v_{ijab}\hat{c}^{\dagger}_a\hat{c}_b^{\dagger}\hat{c}_j\hat{c}_i,
Exponential of one body part can be calculated in \(O(N^3)\) time, but that of the two-body part very expensive to do exactly.
Approximations:
- Hartree-Fock or DFT: replace operator terms with scalar mean values
\hat{c}_a^{\dagger}\hat{c}_b^{\dagger}\hat{c}_j\hat{c}_i\rightarrow \hat{c}_a^{\dagger}\hat{c}_i\langle\hat{c}_b^{\dagger}\hat{c}_j\rangle-\hat{c}_a^{\dagger}\hat{c}_j\langle\hat{c}_b^{\dagger}\hat{c}_i\rangle
- AFQMC: Perform Hubbard Stratanovic transform and sample boson fields
e^{-\frac{\tau}{2}\hat{v}^2}=\int\frac{dx}{\sqrt{2\pi}}e^{-\frac{x^2}{2}+i\sqrt{\tau}x\hat{v}}
Sign problem \(\rightarrow\) trial function \(\rightarrow\) multi-Slater
\(\exp(-\tau\hat{H})|\phi\rangle \rightarrow\) ground state, for \(\tau\rightarrow\infty\)
Thank you!
supergroup3
By Ankit Mahajan
