演算法
講者:Arashi
日期:2020/03/22
大綱
- 甚麼是演算法
- 分治法
- 動態規劃法
- 實作
- 參考資源
甚麼是演算法
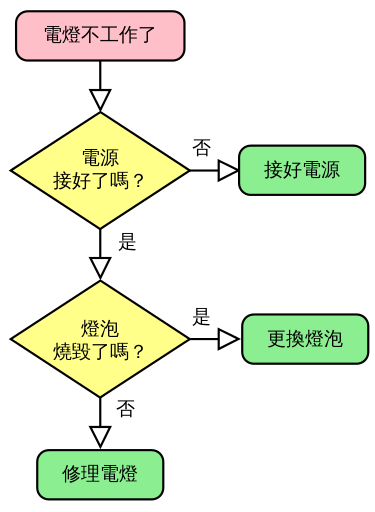
應對燈泡不亮的簡單演算法流程圖
- 輸入必為0個以上
- 輸出必為1個以上的輸出量
- 演算法的描述必須明確
- 有限性
- 有效性
特色
分治法
- 可以解決較複雜的問題
- 在子問題相互獨立的情況下,效率高
- 多寫為遞迴關係式
特色
- 分解問題
- 解決子問題
- 合併解
步驟
動態規劃法
- 適用於有重疊子問題和最佳子結構性質的問題
- 避免計算已經算過的事物
- 子問題的解不會再改變
特色
- 劃分問題
- 確定狀態和狀態變量
- 確定狀態轉移過程
- 尋找終止條件
步驟
實作
費氏數列

分治法解法
- 分解問題:找到第n位的費氏數列的數字
-
解決子問題:找到(n-1) + (n-2) 的值
- 合併解:把找到的值回傳後加起來
分治法解答
def count(n):
if st[n] != "-1":
return st[n]
if n == 0:
return 0
if n == 1:
return 1
st[n] = count(n-1) + count(n-2)
return st[n]
st = ("-1 " * 10000).split(" ")
n = int(input())
while n != -1:
print(count(n))
n = int(input())動態規劃法解法
- 劃分問題:首先要確認要找到第幾位的數字,再來看看這個數字有沒有被算過,有的話直接回傳,沒有則繼續往下計算。
- 確認狀態:需要紀錄:每一位的數字,存放處:建立一個 list。
- 轉移過程:將要紀錄的內容放入 list。
- 終止條件:要找的位數有在 list 中。
動態規劃法解答
def count(n):
if n == 0:
return 0
if n == 1:
return 1
return count(n-1) + count(n-2)
n = int(input())
print(count(n))參考資源
演算法 - 維基百科. Retrieved from https://zh.wikipedia.org/wiki/%E7%AE%97%E6%B3%95
動態規劃 - 維基百科.Retrieved from https://zh.wikipedia.org/wiki/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92
分治法:維基百科.Retrieved from https://zh.wikipedia.org/wiki/%E5%88%86%E6%B2%BB%E6%B3%95
[Leetcode][分治法]相關題目匯總/分析/總結.Retrieved from https://blog.csdn.net/qqxx6661/article/details/81568563
Ch15 動態規劃.Retrieved from https://hackmd.io/@qR5cY2d3Ql2AdYtLfHFxVg/ByZgGkLpW?type=view
參考資源
Thanks for listening
演算法
By arashi
演算法
- 107



