Quantization and Neural Networks
-
Why is there a need for quantization?
-
Quantization in TPUs
-
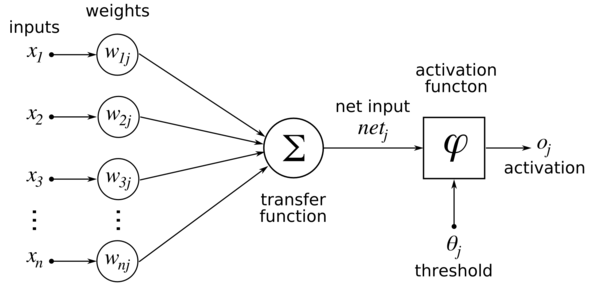
How does Mapping work?
-
Fine Grained Quantization
-
Quantization: A boon or a bane?

About Me
- Archana Iyer
- Deep Learning Intern at Saama
- B. Tech. Electrical and Electronics
- Next Tech Lab
- www.saama.com/blog/quantization-need-tpus/
Why is there a need for Quantization?
- Imagine a play in a small theatre, where you are a producer sitting with the audience
- Let us suppose the actors are weights and there are rows and rows of TPUs/GPUs behind.
- The director has assured you that they have rehearsed the play about 10 times, now all you do is pray that the performance goes well
- Optimization of tasks is necessary for a play if you have a lot of things to do and lot fewer individuals.


Quantization and TPUs

Text
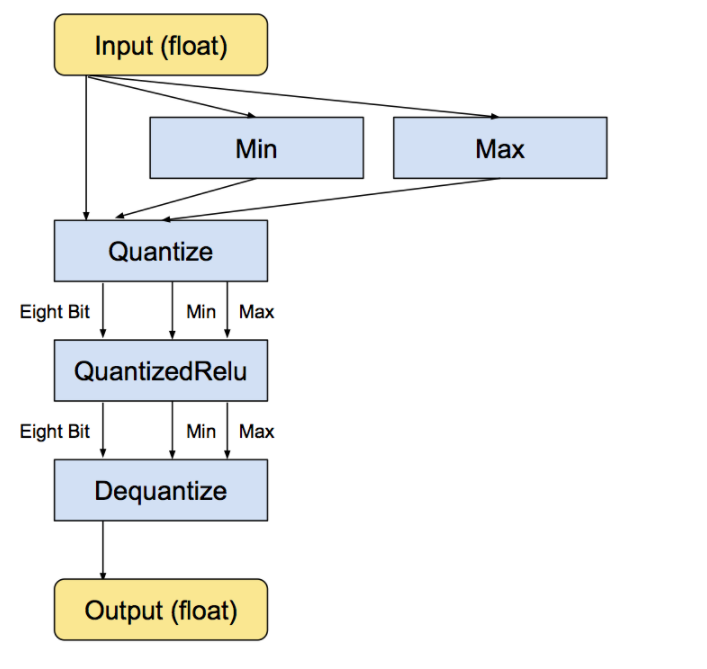
Quantization was introduced in TPUs so that large computations can be mapped to a smaller bit, let us know look into how a simple ReLU operation takes place
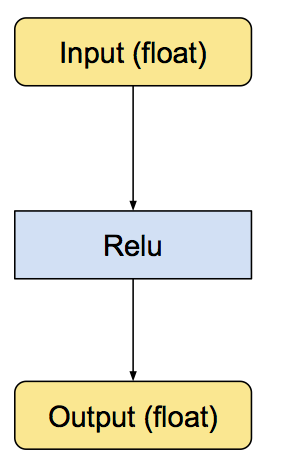
Orginal ReLU operation
ReLU operations with the internal conversion.
The min and max operations actually look at the values in the input float tensor and then feeds them into the Dequantize operation that converts the tensor into eight-bits
How does Mapping work?
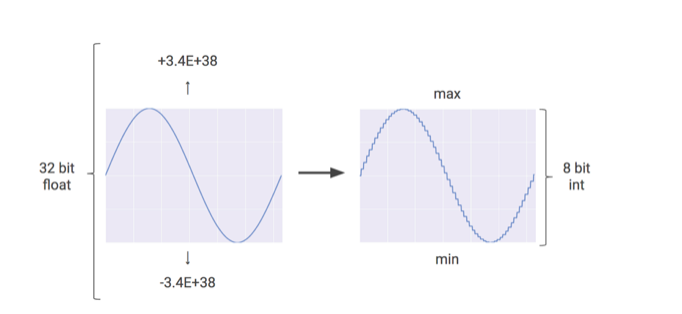
- 32 bit has a higher computation, hence requires more computational resources and memory space
- Hence it is preferable that 32 bit be mapped to an 8 bit, during inference hence saving a lot of resources
TensorFlow has recently released an API that converts 32-bit floating-point integers into 8-bit integers.
-
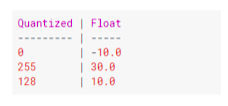
Generally, all weight values in the neural network are in a small range. Say, for example, from -8.342343353543f to 23.35442342554f. In TensorFlow, while doing quantization, the least value is equated to 0 and the maximum value to 255. All the values in between are scaled inside the 0 to 255 range.


Importance of Edge Computing for Quantization
The edge is the part of the system that is closest to the source of data. It includes sensors, sensing infrastructures, machines, and the object being sensed. The edge actively works to sense, store, and send that data to the cloud.
However, the problem with this approach is that most of the analytics work is computationally very expensive and the edge systems (which are usually simple microcontrollers) cannot handle these calculations.
In this case, quantization can be a boon. Changing the computation from 32-bit to 8-bit floating point numerical has been shown to reduce computational tasks, at times, by up to 30% without a significant reduction in accuracy.


Fine-Grained Quantization-
Based on Paper: Ternary Neural Networks with Fine-Grained Quantization by Abhisek Kundu, Researcher Parallel Computing Lab, Intel Labs, Bangalore, India
- Ternary weight networks
- Importance of Edge Devices to Quantization
- Weight and Activations Quantization
- Ternary Conversion of Neural Network
- Non-Generalised values of delta and alpha
- Results

Ternary Weight Networks
- Ternary weight networks (TWNs) - neural networks with weights constrained to +1, 0 and -1.
- With better DNN models we are moving to a better use case like putting them into smartphones and embedded devices
- Drawbacks with DNNs: limited storage battery power, and computer capabilities of the small embedded devices
- TWNs evolved from BWNs(Binary Weight Neural Networks)
- Formulation
α ∗ ,Wt∗ = arg min α,Wt J(α,Wt ) = ||W − αWt ||2 2 s.t. α ≥ 0, Wt i ∈ {−1, 0, 1}, i = 1, 2, . . . , n

Weight and Activations Quantization
-
Previous papers used to quantize only the weights and not the inputs(activations) during inference
- Fetching inputs and weights from memory takes up most of the computational power
- Therefore we quantize weights and inputs
- Quantization is done on the trained network so as to reduce the error during inference

Ternary Conversion of Neural Network
- Convert Weights to (-a, 0, a); a>0, without re-training
-
Use a threshold D>0

- We convert weights W such that they are of the form {-a, 0, a}
- The Error E(a, D) = ||W - a|| ^ 2
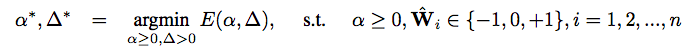
Grouping of alpha and delta values

- Weights across a Neural Network can have different Distributions
- So we group weights according to their weight distribution and then find the values of a and D
- Weights may not have a mean
at 0 so we use positive and negative values of D
Non-Generalised values of delta and alpha
-
Important to remember that they are not performing any retraining.


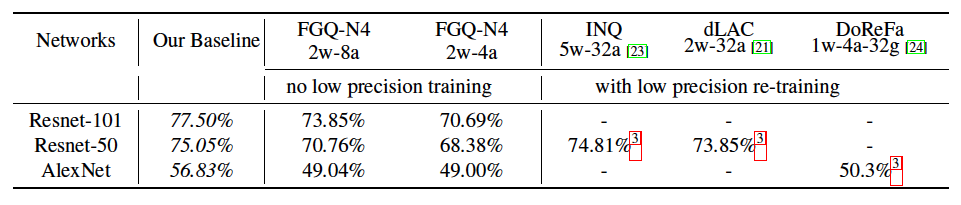
Results

Quantization: Boon or Bane?

-
Computational Resources
-
Memory
-
Reducing Time
-
Accuracy:
Take self-driving cars, for example, where a difference of a few percentages could make the difference between a safe drive and a crash. So while quantization is powerful, as it can make computing a lot faster, its applications should be considered carefully.

Reach Out?
- a.iyer@saama.com
- Appreciate your feedback on Facebook and LinkedIn
- https://www.facebook.com/archana.iyer.73
- You can check out the deck at: https://slides.com/archanaiyer/deck


deck
By archana iyer
deck
- 1,166



