Einstein's gravity
What must be kept
\begin{aligned}
&\blacktriangleright \Gamma_{\nu \sigma}^\mu &\text{ ( Christoffel symbols) }\\
&\blacktriangleright \frac{d^2 x^\mu}{ds^2} + \Gamma_{\nu\sigma}^\mu \frac{dx^\nu}{ds}\frac{dx^\sigma
}{ds} = 0 &\text{ (Geodesic equation)}\\
&\blacktriangleright R_{\mu \nu \kappa}^\lambda & \text{ (Riemann tensor )}\\
&\blacktriangleright ds^2 = -B(r)dt^2 + A(r)dr^2 + r^2 d\theta^2 + r^2\sin^2\theta d \phi^2 & \text{ (Schwarzschild solution) }
\end{aligned}
Einstein's gravity
What can we change
Einstein-Hilbert action
Schwarzschild solution and its Newtonian limit
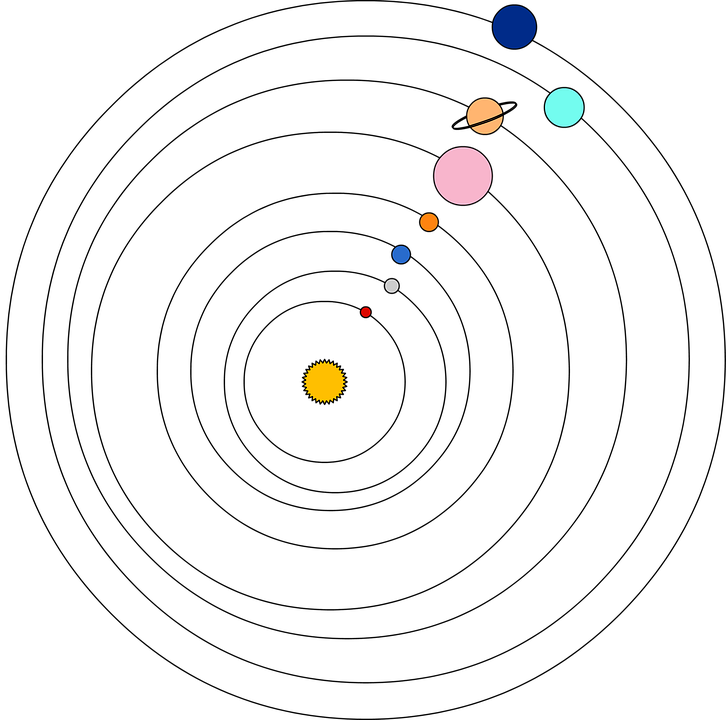
That is also why we are free to add a ~Λ term
I_\text{EH} = -\frac{1}{16\pi G} \int d^4 x \; \sqrt{-g} \; R^\alpha_{\;\;\alpha}
Einstein's gravity
Problems
-\frac{1}{8\pi G}\left(R^{\mu\nu} - \frac{1}{2}g^{\mu\nu}R^{\alpha}_{\;\;\alpha}\right) = T_M^{\mu\nu}
Einstein's equations
Work very well in Solar System scales, but when we extrapolate to:
- Galactic scales ---> Dark Matter problem.
- Cosmological scales ---> Dark Energy / Λ problem.
- Strong gravity ---> Singularities.
- Quantization ---> Not renormalizable.
Weyl / Conformal transformation
g_{\mu\nu} \longrightarrow e^{2 \alpha(x)} g_{\mu\nu}(x)
The EH action is not invariant under this transformation,
however there is unique action given by
I_\text{W} = -\alpha_g \int d^4 x \; \sqrt{-g}\; C_{\lambda\mu\nu\kappa} C^{\lambda\mu\nu\kappa}
which is conformally invariant.
Why should we care about Weyl invariance?
Supose we have a free massless fermion
\psi(x)
Imposing invariance under local phase transformations,
\mathcal L = (\partial^\mu \psi)^\dag (\partial_{\mu} \psi)
D_\mu = \partial_\mu + ieA_\mu(x)
Covariant derivative
"Photon"
gives us electromagnetism.
\psi \longrightarrow e^{i\alpha(x)} \psi(x)
Why should we care about Weyl invariance?
Similarly, if we ask the theory to be invariant under local coordinate transformations,
\psi \longrightarrow e^{i \omega_{\mu\nu}(x) M^{\mu\nu}} \psi(x)
Lorentz transformation
we then need a new field,
\Gamma(x)
, which gives us local Weyl invariance for free!
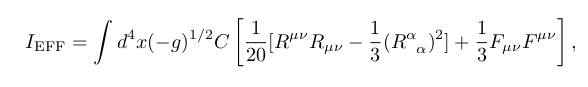
If we then evaluate Feynman's path integral, the effective action is
Conformal gravity action !
Now, what happens if we have a massive fermion?
Standard Model
If we ignore the mass ( i.e. Higgs field), then the Standard Model is conformally invariant.
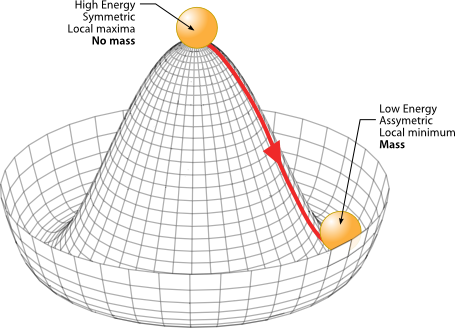
However, mass and length scale break conformal invariance. The mass is generated through the dynamics of the Higgs field
V(\phi) = -\mu^2 | \phi |^2 + \lambda | \phi | ^4
Conformal gravity
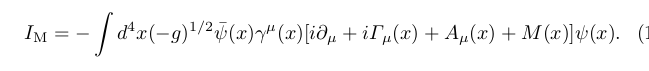
path integral formalism again...
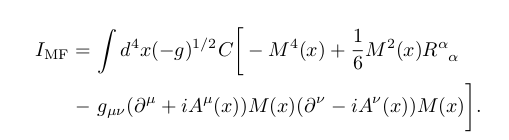
We get a Higgs potential with the Ricci scalar being the one thats gives it the Mexican hat shape!
Quantization
I_\text{W} = -\alpha_g \int d^4 x \; \sqrt{-g}\; C_{\lambda\mu\nu\kappa} C^{\lambda\mu\nu\kappa}
Unitless ----> Theory is renormalizable
Quantization
If gravity is quantized, then
T_{\mu\nu} = T^{\mu\nu}_\text{matter} + T^{\mu\nu}_\text{gravity}
So the vacuum solution is no longer
T^{\mu\nu}_\text{matter} = 0
T_{\mu\nu} = T^{\mu\nu}_\text{matter} + T^{\mu\nu}_\text{gravity} = 0
but rather
Quantization
Dark matter
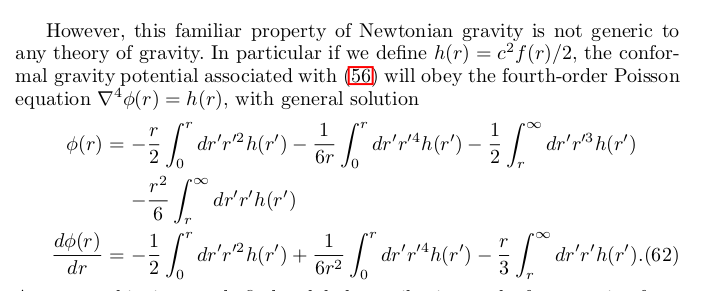
This integrates the entire Universe.
Dark matter
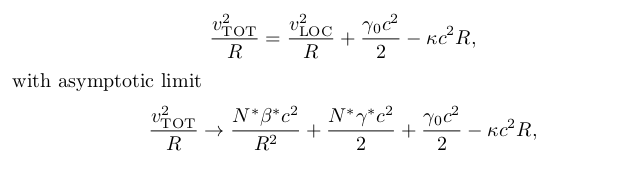
Value given by the Solar System
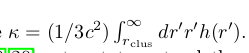
Contribution from the whole universe
Dark matter
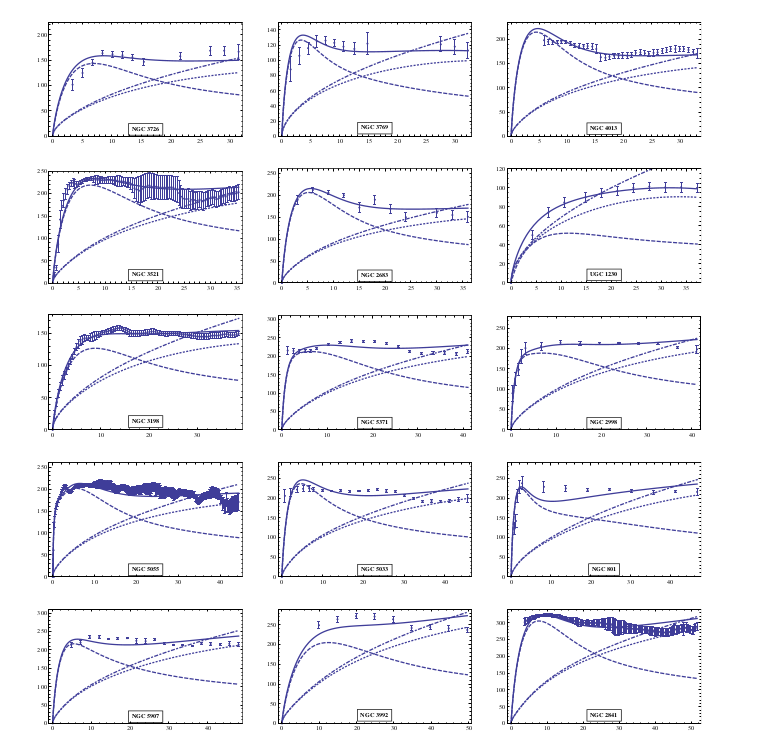
138 galaxies fitted with two free parameters.
Dark energy
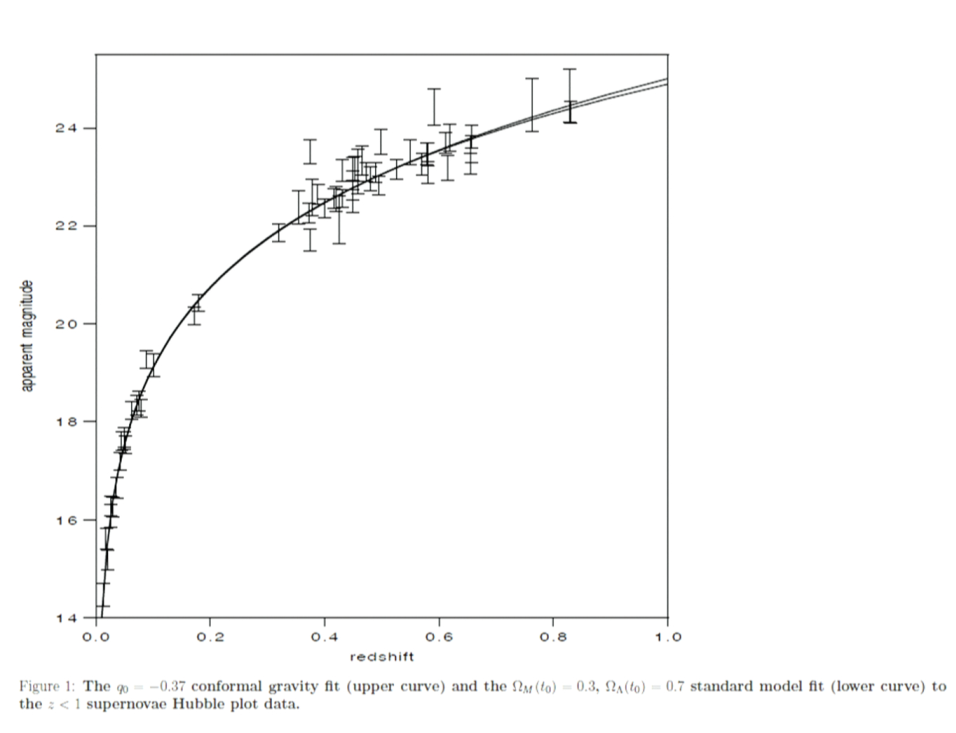
Conformal Gravity
By arnauqb
Conformal Gravity
Making the case for conformal gravity (2012).
