Intro to Model Compression

4/30 by Arvin Liu

Video Explanation

Knowledge Distillation

Network Pruning

Review

Network Pruning

方法：將Network不重要的weight或neuron進行刪除，再重train一次。
原因：大NN有很多冗參數，而小NN很難train，那就用大NN刪成小NN就好了。

應用：只要他是NN（？）就可以。

Knowledge Distillation

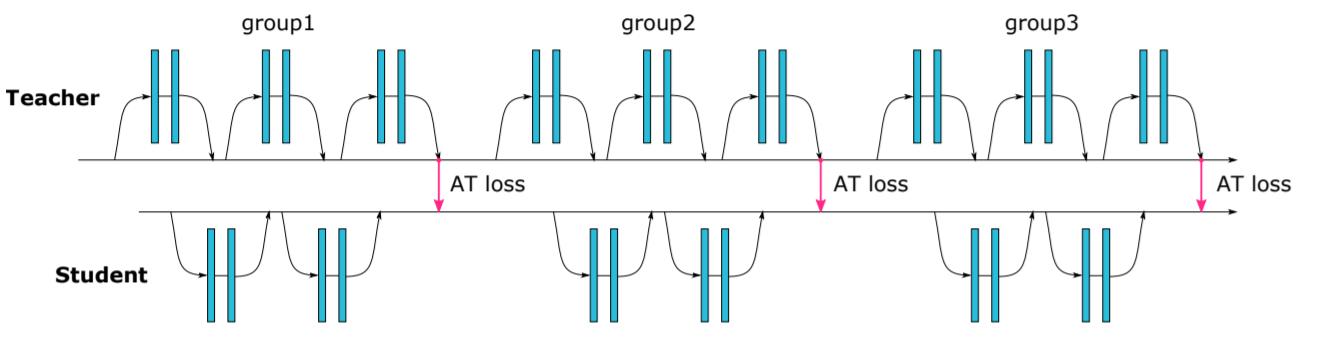
方法：利用一個已經學好的大model，來教小model如何做好任務。
原因：讓學生直接做對題目太難了，可以讓他偷看老師是怎麼想/解出題目的。

應用：通常只用在Classification，而且學生只能從頭學起。

Review

Architecture
Design

方法：利用更少的參數來達到原本某些layer的效果。
原因：有些Layer可能參數就是很冗，例如DNN就是個明顯例子。

應用：就是直接套新的model，或是利用新的layer來模擬舊的layer。

Parameter Quantization

方法：將原本NN常用的計算單位：float32/float64壓縮成更小的單位。
原因：對NN來說，LSB可能不是那麼的重要。

應用：對所有已經train好的model使用，或者邊train邊引誘model去quantize。

* LSB: Least-Significant Bit, 在這裡指小數點的後面其實很冗。

Why Learn'em all?

Mixed it !

例如你可以這樣混合。

ResNet101

巨肥胖Model

MobileNet

小小Model

 Architecture

Design

Knowledge

Distillation

MobileNet

-pruned

Network  Pruning

Quantization

(Fine-tune or Finalize)

.

Knowledge Distillation

Knowledge Distillation

Main Question: Distill what?

  • Logits (輸出值)
    • 直接匹配logits
    • 學習一個batch裡面的logits distribution
    • ...
  • Feature (中間值)
    • 直接匹配中間的Feature
    • 學習Feature中間如何轉換
    • ...

Before Logits KD...

You need to know the magic power of soften label.

Info you know before

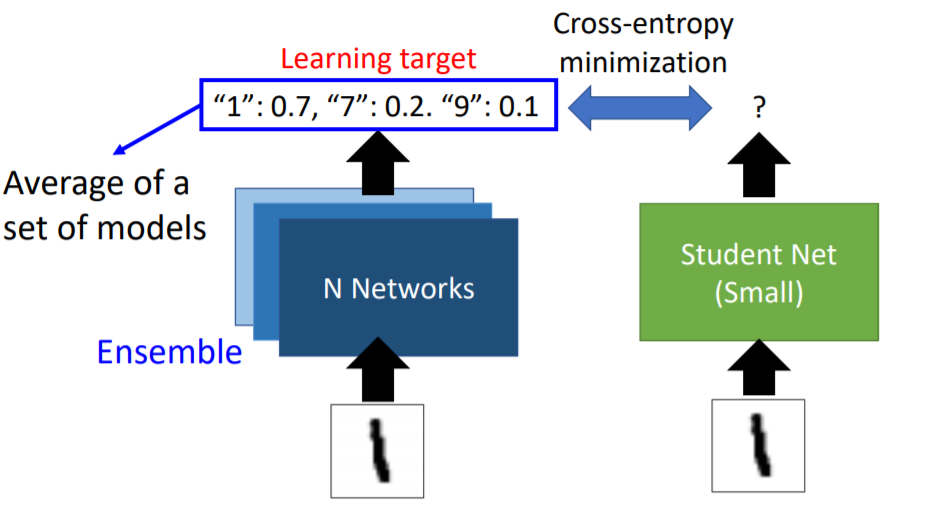
Hidden information in relationship between categories

Overfit(?) in Model

Model

Incompleteness

Crop (Augment)

Inconsistency

Label Refinery

  1. train一個model C0，目標label為GT。
  2. train一個model C1，目標label為C0的輸出。
  3. train一個model C2，目標label為C1的輸出。
  4. 一直往下train，train到精度不再提升為止。

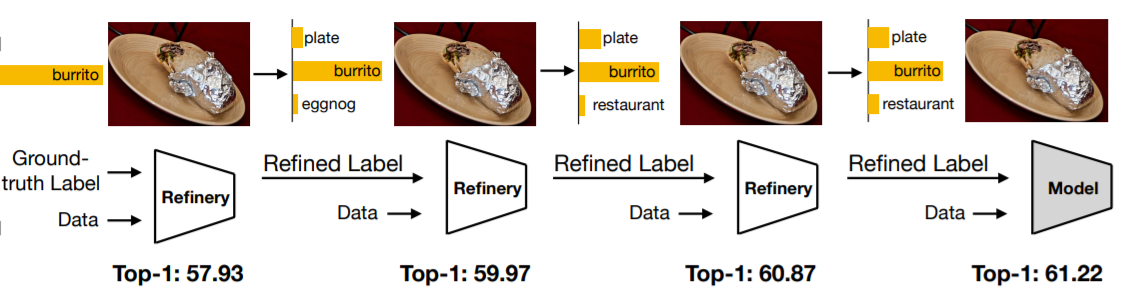
每次Refined的時候都可以降低Incompleteness & Inconsistency, 並且還可學到label間的關係

Logits Distillation

透過 soft target讓小model可以學到class之間的關係。

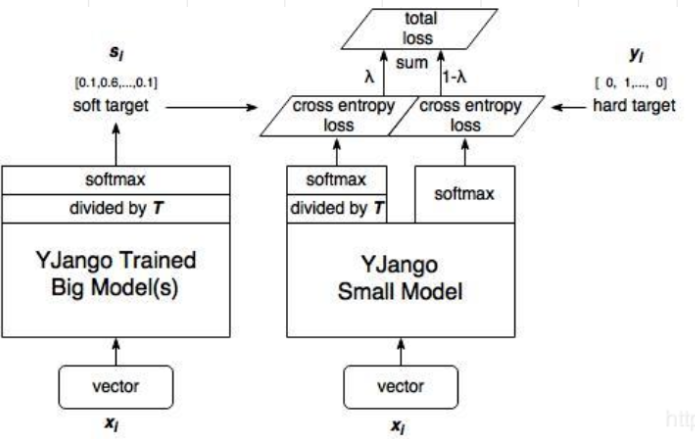
Distill Logits - Baseline KD

Distill Logits - Deep Mutual Learning (1/3)

讓兩個Network同時train，並互相學習對方的logits。

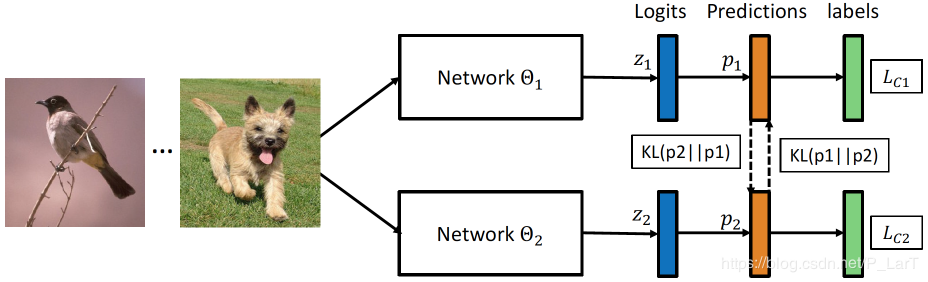
Distill Logits - Deep Mutual Learning (2/3)

Logits

y_{1,t}
y_{2,t}
x

Networks2

Networks1

Step 1: Update Net1

y

True Label

CE

D_{KL}(y_{2,t}||y_{1,t})
Loss_1 = D_{KL}(y_{2,t}||y_{1,t})+ \text{CrossEntropy}(y,y_{1,t})

Distill Logits - Deep Mutual Learning (3/3)

Logits

y_{1,t}
y_{2,t}
x

Networks2

Networks1

Step 2: Update Net2

y

True Label

CE

D_{KL}(y_{1,t}||y_{2,t})
Loss_2 = D_{KL}(y_{1,t}||y_{2,t})+ \text{CrossEntropy}(y,y_{2,t})

More Details: https://slides.com/arvinliu/kd_mutual

Distill Logits - Born Again Neural Networks

  1. 初始Model是KD來的。
  2. 迭代使用Cross Entropy。
  3. 最後Ensemble 所有Student Model。

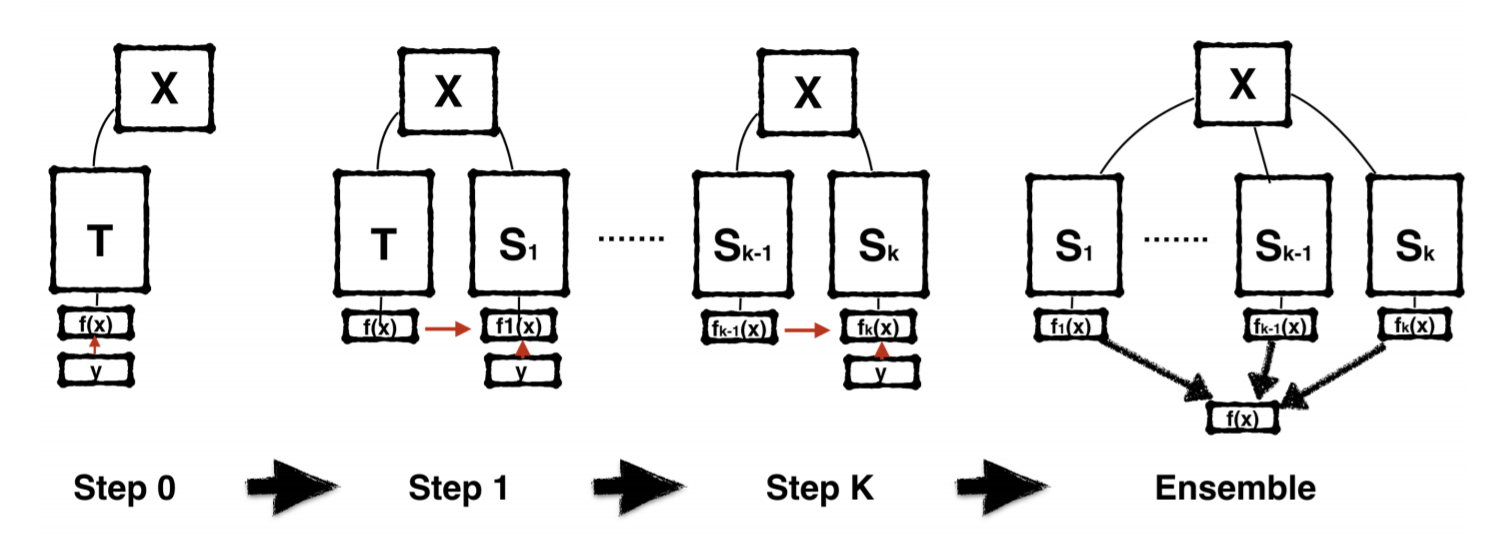
Similar with label refinery很像。僅差異於:

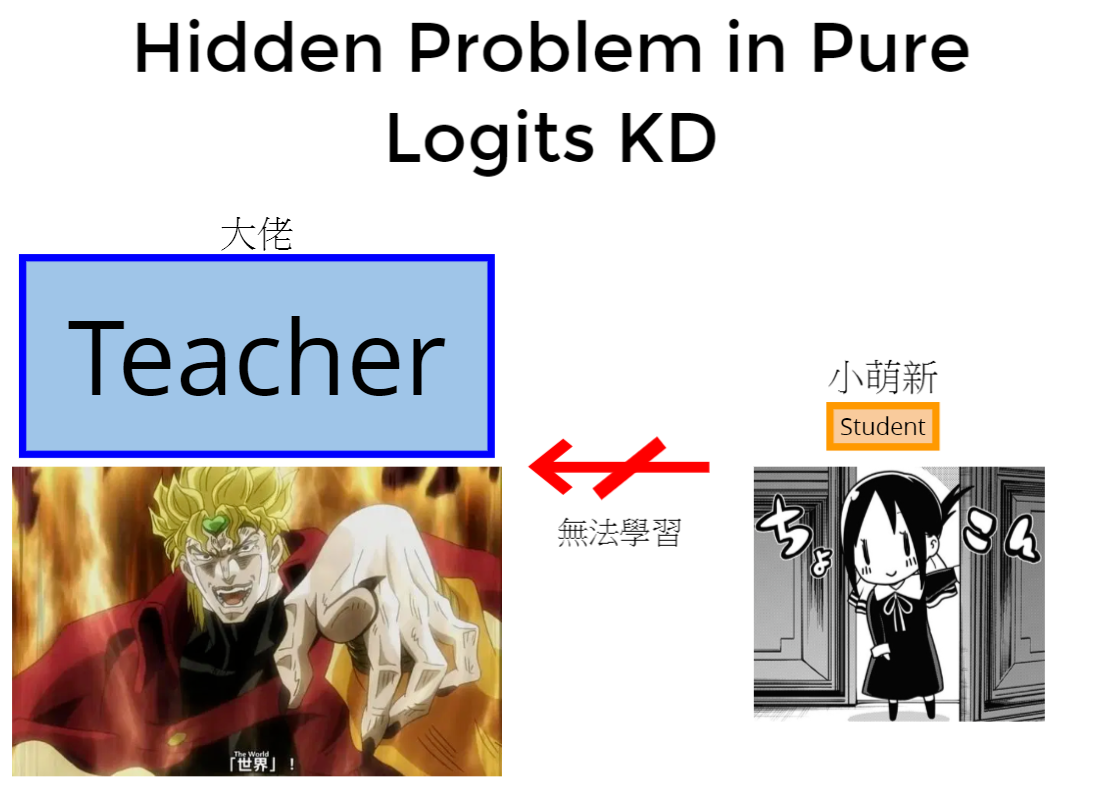
Hidden Problem in Pure Logits KD

Student

Teacher

大佬

小萌新

無法學習

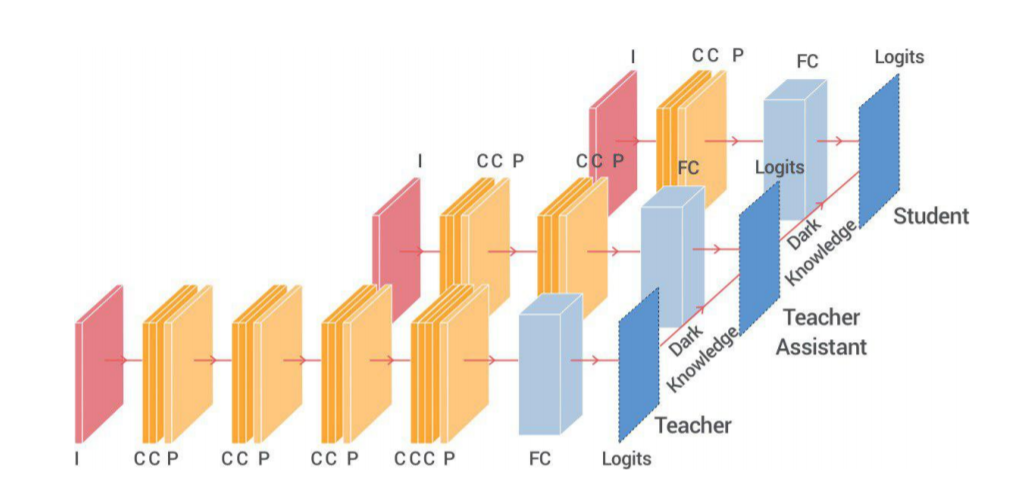
Distill Logits - TAKD

用一個參數量介於Teacher&Student的TA做中間人來幫助Student學習，以此避免model差距過大學不好。

Feature Distillation

Why Distill Feature?

Teacher

Student

Only one loop

No end point

ans: 0
next ans: 8

Distill Feature - FitNet (1/3)

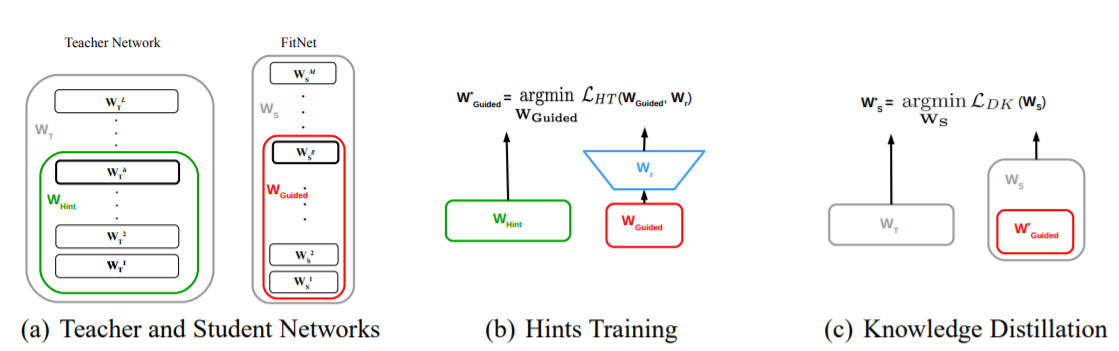
先讓Student學習如何產生Teacher的中間Feature，之後再使用Baseline KD。

Distill Feature - FitNet (2/3)

Teacher Net

Student Net

Logits

y_{t}
y_{s}
x
W_{r}

Fit

(in 2-norm distance)

Step 1: Fit feature

Distill Feature - FitNet (3/3)

Teacher Net

Perform Baseline KD

Logits

y_{t}
y_{s}
x

Student Net

Step 2: Fit logits

  • 架構越相近，效果越好。

Hidden Problems in FitNet (1/2)

Teacher Net

Student Net

Logits

???

Distill Feature

  1. Model capacity is different

  2. There's lots of redundancy in Teacher Net.

Hidden Problems in FitNet (2/2)

Teacher Net

Logits

Text

H

W

C

H

W

1

Knowledge

Compression

Feature Map

Maybe we can solve by following steps:

Distill Feature - Attention (1/2)

讓Student學習Teacher的Attention Map以此引導。

Distill Feature - Attention (2/2)

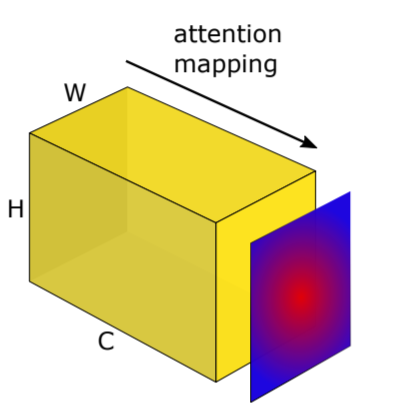
  • How to generate attention map?
    • 將(W, H, C)的weight各自平方後加成(W, H)的矩陣 T。
    • Attention map =T/norm(M)。
       
  • What target function?
    • L2 distance between teacher's attention map & student's attention map.

Can we learn something from batch?

Relational Distillation

Distill Relation - Relational KD (1/3)

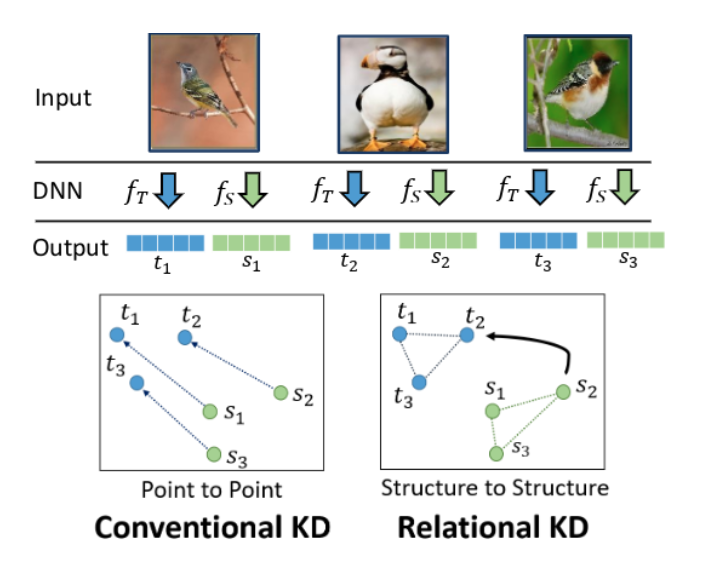
Individual KD : 以每個sample為單位做知識蒸餾。

Relational KD: 以sample之間的關係做知識蒸餾。

Distill Relation - Relational KD (2/3)

t : teacher's logits

s : student's logits

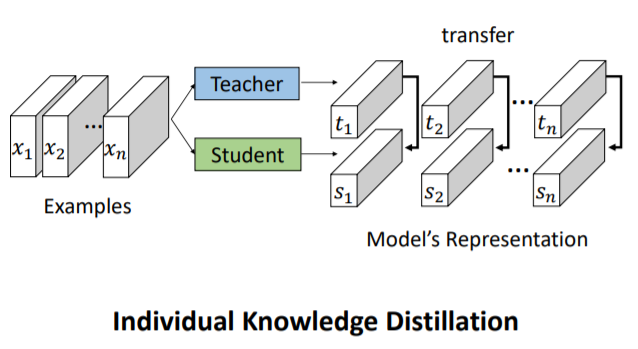
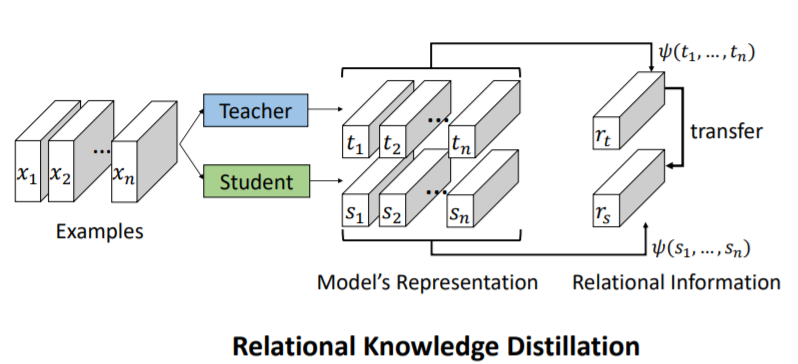
Individual KD:

Student learn Teacher's output

Relational KD:

Student learn model's representation

Logits Distribution / Relationship

is kind of relational information

Distill Relation - Relational KD (3/3)

Distance-wise KD

t_1
t_2
t_3

t : teacher's logits

s : student's logits

s_1
s_2
s_3

~=

~=

Angle-wise KD

t_1
t_2
t_3
s_1
s_2
s_3

~=

Why not distill relational information between feature?

Of course you can.

Distill Relation - Similarity-Preserving KD (1/3)

Mnist Model

circle

vertical line

0

9

1

[1, 0]

[1, 1]

[0, 1]

1 0.7 0
0.7 1 0.7
0 0.7 1

Cosine Similarity

\text{img}_0
\text{img}_1
\text{img}_2
\text{img}_1
\text{img}_2
\text{img}_0

Distill Relation - Similarity-Preserving KD (2/3)

Mnist TeacherNet

circle

vertical line

Relational Information

on Features

1 0.7 0
0.7 1 0.7
0 0.7 1

Teacher's Cosine Similarity Table

\text{img}_0
\text{img}_1
\text{img}_2
\text{img}_1
\text{img}_2
\text{img}_0

Mnist StudentNet

?

?

Relational Information

on Features

Student's Cosine Similarity Table

imitate to learn relationship between images

No hard copy to features!

Distill Relation - Similarity-Preserving KD (3/3)

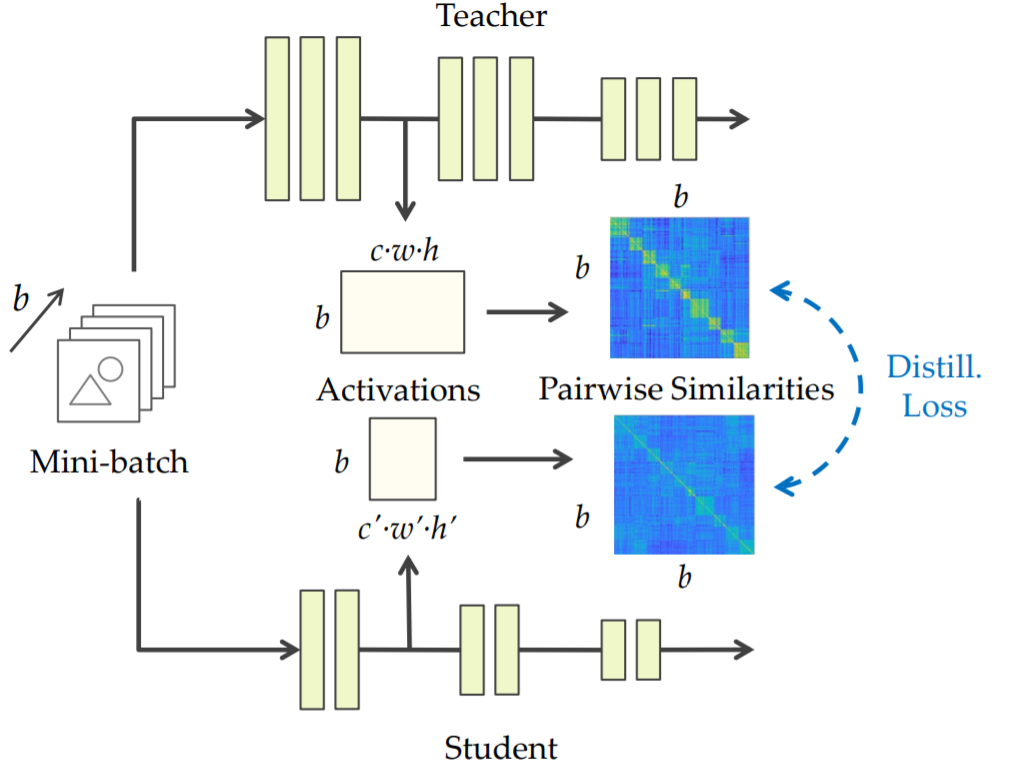
蒸餾兩兩sample的activation相似性。

Network Pruning

Neuron Pruning in DNN (a=4, b=3, c=2)

Text

Dense(4, 3)

Dense(3, 2)

Dense(2, 2)

Dense(4, 2)

(3,2) Matrix

(4,3) Matrix

(2,2) Matrix

(4,2) Matrix

traivial

Feature 0~3

Feature 0~3

Param Changes:

(a+c) * b ->
(a+c) * (b-1)

Neuron Pruning in DNN

Neuron Pruning in CNN

Text

Conv(4, 3, 3)

(3, 2, 3, 3) Matrix

traivial

Feature map 0~3

Feature map 0~3

Conv(3, 2, 3)

(4, 3, 3, 3) Matrix

Conv(4, 2, 3)

(2, 2, 3, 3) Matrix

Conv(2, 2, 3)

(4, 2, 3, 3) Matrix

Param Changes:

(a+c) * b * k * k ->
(a+c) * (b-1) * k * k

Neuron Pruning in CNN (a=4, b=3, c=2)

Network Pruning

Main Question: Prune what?

  • Evaluate by Weight
  • Evaluate by Activation
  • Evaluate by Gradient

After Evalutaion?

  • Sort by importance and prune by rank.
  • prune by handcrafted threshold.
  • prune by generated threshold.

Which is most important?

 

How to evaluate importance?

Threshold or Rank?

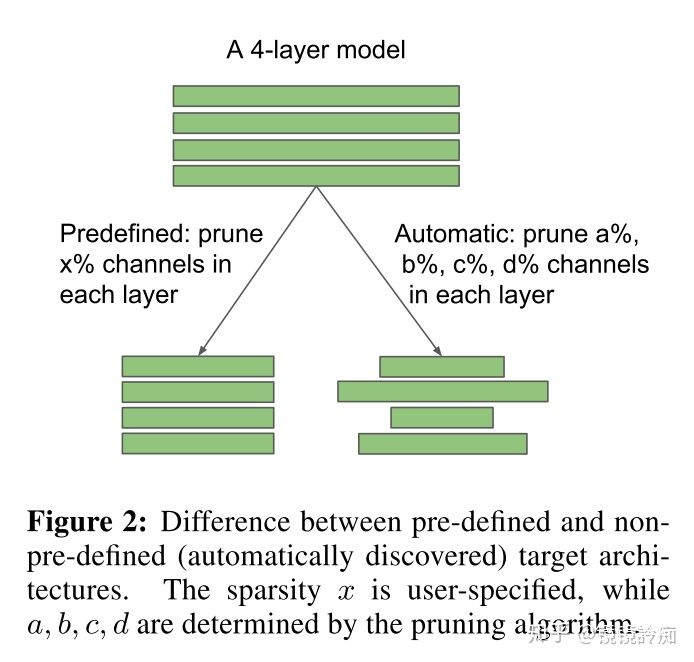
Evaluate Importance

Eval by weight - sum of L1 norm

Layer want to pruned

\sum ^{4}_{j=1}||k_{1,j}||
  • Change to L2 norm?

Feature map 0~3

Conv

Conv Weight:

(3, 4, k, k)

calculate sum of L1-norm

\sum ^{4}_{j=1}||k_{2,j}||
\sum ^{4}_{j=1}||k_{3,j}||

Prune

Eval by weight - FPGM (1/4)

Ideal case for pruning by L-norm:

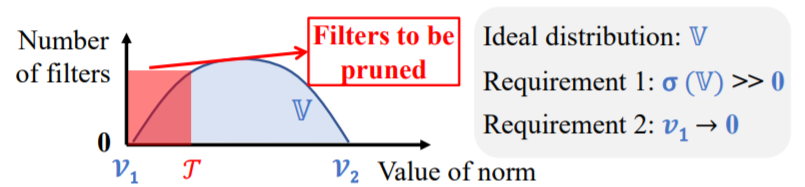
Filter Pruning via Geometric Media

Conv Weight:

(3, 4, k, k)

norm_1
norm_2
norm_3

Distribution

Distribution we hope

Eval by weight - FPGM (2/4)

Hazard of pruning by L-norm:

1. σ(V) must be large.

2. there's V close to 0.

Difficult to find an appropriate threshold.

All filters are non-trivial.

Filter Pruning via Geometric Media

Eval by weight - FPGM (3/4)

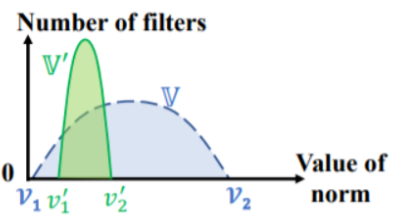
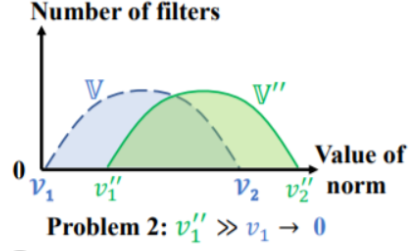
Redundancy by pruning by L-norm:

Filter Pruning via Geometric Media

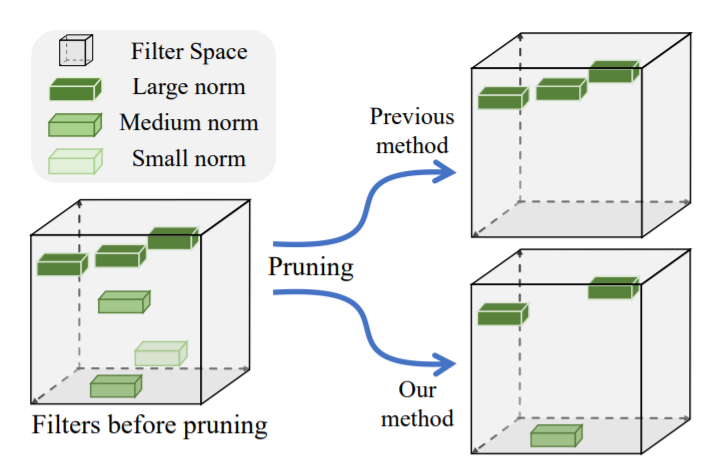
Maybe there're multiple filters with same function.

Pruning by Geometric Media can solve the problem.

Eval by weight - FPGM (4/4)

Find Geometric Media in CNN

Filter Pruning via Geometric Media

Feature map 0~3

Conv

Conv Weight:

(3, 4, k, k)

Choose GM(s)  and prune others

Other parameters we can use?

Eval by BN's γ  - Network Slimming (1/2)

Feature map 0~3

Conv

Batch Normalization

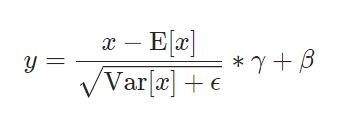
Pytorch's BN 

  • γ is a learnable vector.
  • We can just use this parameters to evaluate importance.
  • colab tutorial (only pruned by gamma)

Eval by BN's γ  - Network Slimming (2/2)

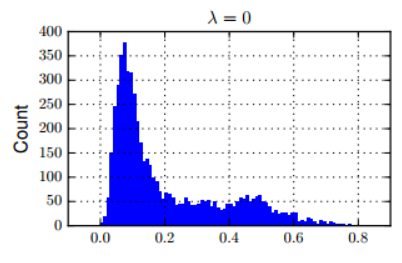
  • Without constraint, γ's distribution may hard to prune. (Because lots of γ is non-trivial.)
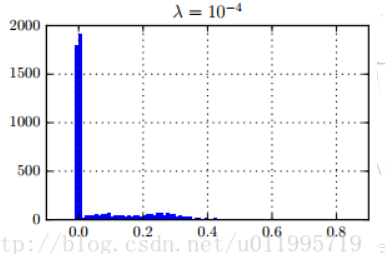
  • After adding L1-penalty on γ, γ's distribution is good enough to prune.

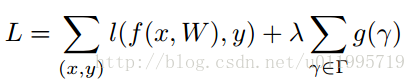
* g is L1-norm.

Eval by 0s after ReLU - APoZ (1/2)

Average Percentage of Zeros

Data

Feature map 0~3

ReLU

  • Calculate APoZ (Avg % of Zeros) in each feature maps

Conv

Neuron is not a number, like

Feature Map with shape (n,m)

Sum of it !

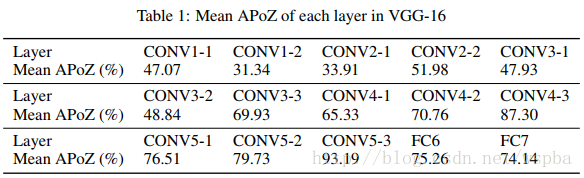
APoZ is much than you think.

Eval by 0s after ReLU - APoZ (2/2)

Average Percentage of Zeros

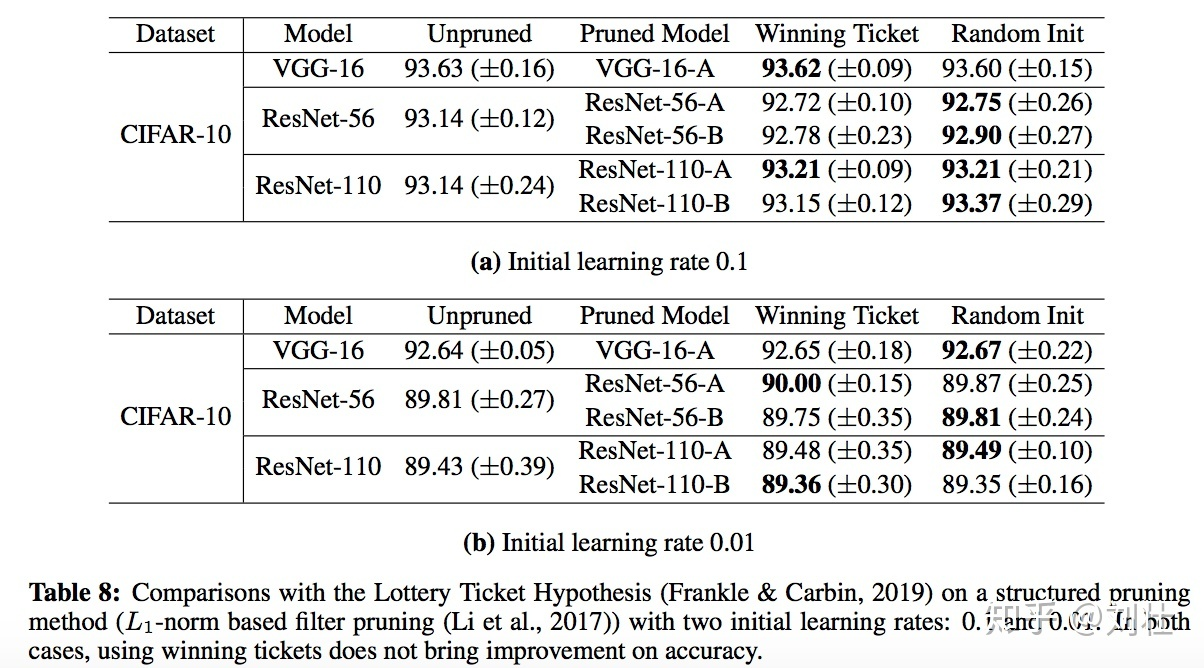
More About Lottery Ticket Hypothesis

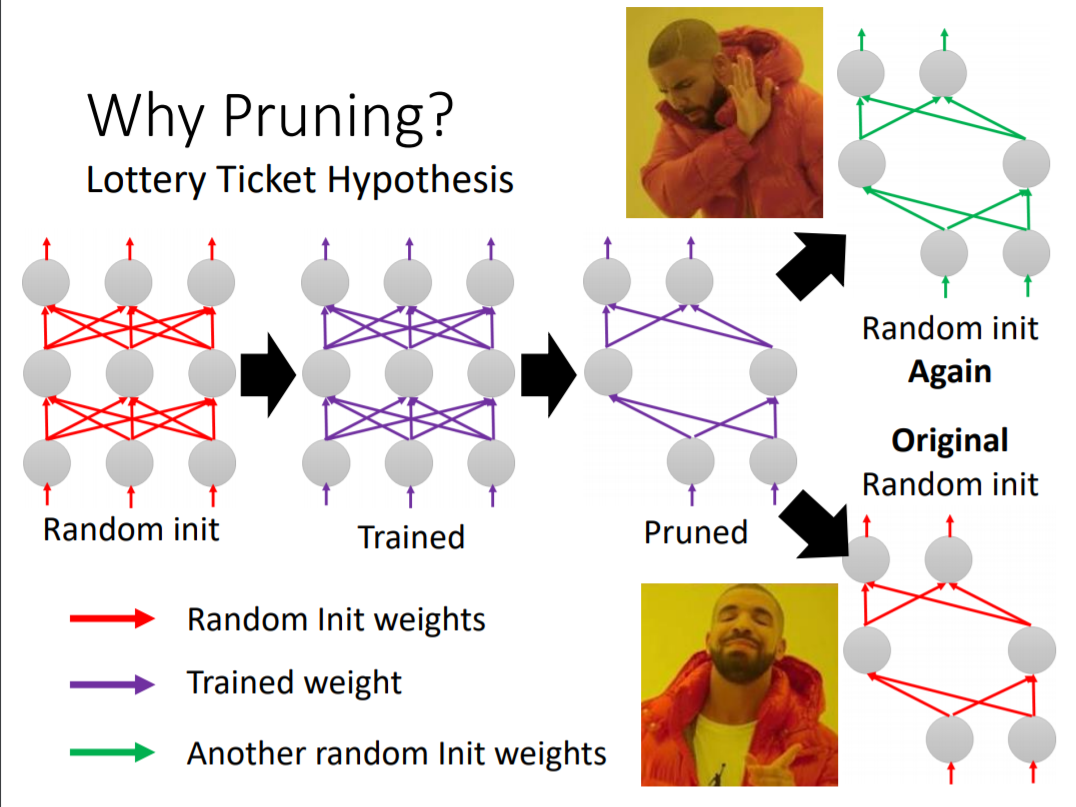
Recap: Lottery Ticket Hypo

Issue 1 : Prune What?

Authors use L1-norm to prune weight. (Not neurons.)

w_{init}
w_{final}

Large

w_{init}

Small

Large

Easier to become winning ticket?

More Meaningful?

(Use w_final as their mask)

w_{final}

Large

Choose which mask?

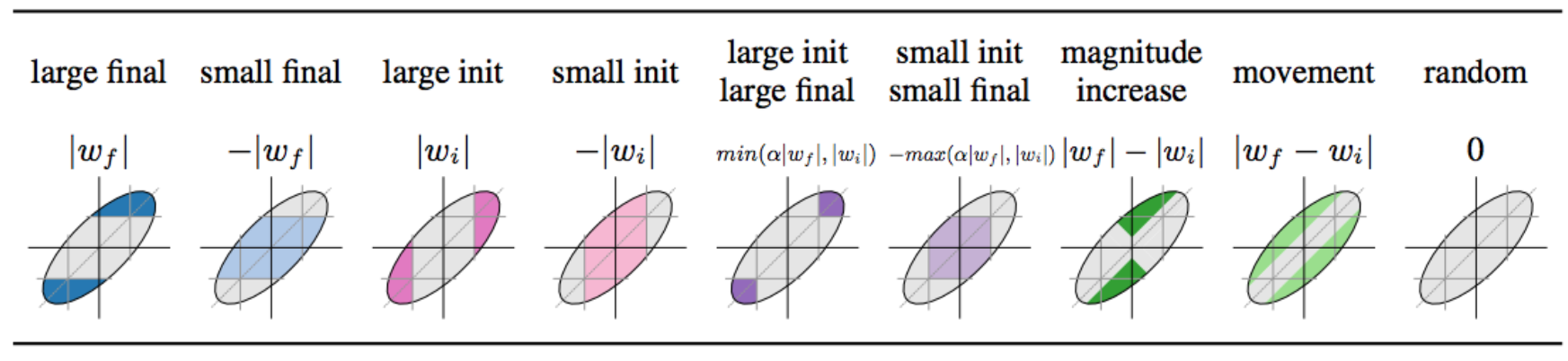
L1-norm pruning

  • x-axis: init weight
  • y-axis: weight after trained
  • gray-zone: masked weight

Experiments 1 - Which Mask

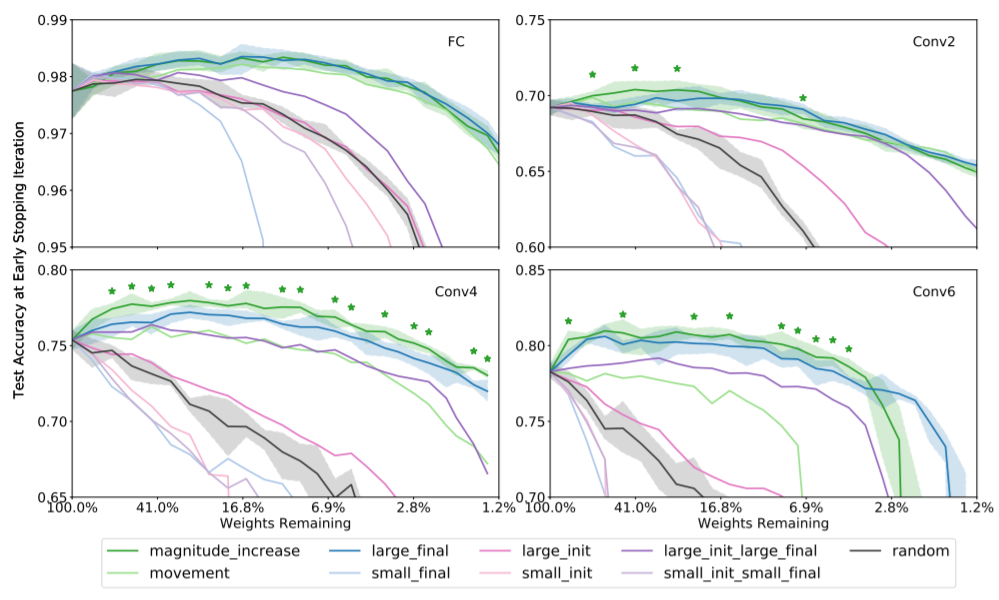
  • magnitude:
  • movement:
|w_f|-|w_i|
|w_f-w_i|

Magnitude & Large_final wins

issue 2 : Winning Tickets property?

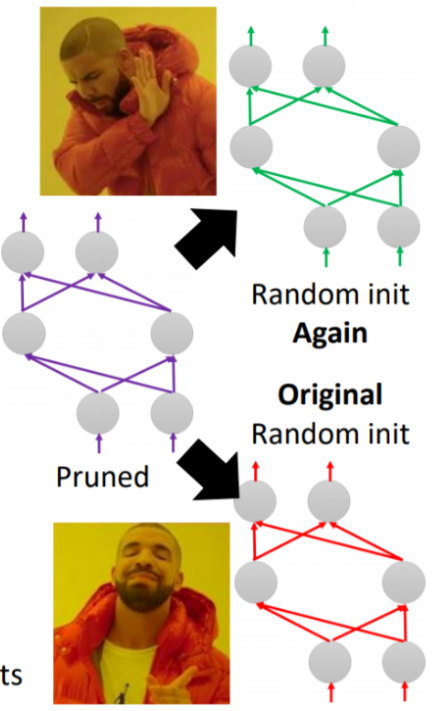
Question: Why winning tickets can perform better accuracy?

Experiment:

  • sign:
    • rewind init sign
    • random
  • value:
    • rewind init value
    • reshuffle weight in same layer
    • constant α (std of initializer)
    • random

Experiment 2 : Winning Tickets property?

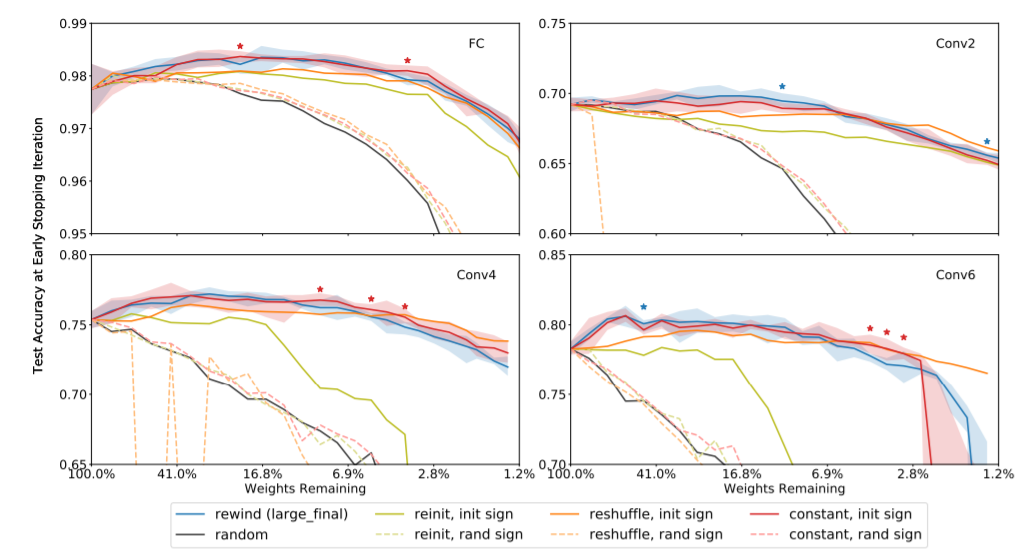
sign is important,

even init value is constant can work.

Conclusion

Experiment 1:  Choose Which Mask

  • Usual L1-norm pruning : 

Experiment 2:  Remain what properties in 

  • Under same architecture, init sign is important.
w

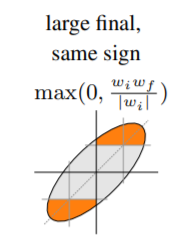
Based on Experiment 1 & 2, we can construct a "supermask".

Rethink vs Lottery

Recap: Rethinking the value of network pruning

Pruning algorithms doesn't learn "network weight", they learn "network structure".

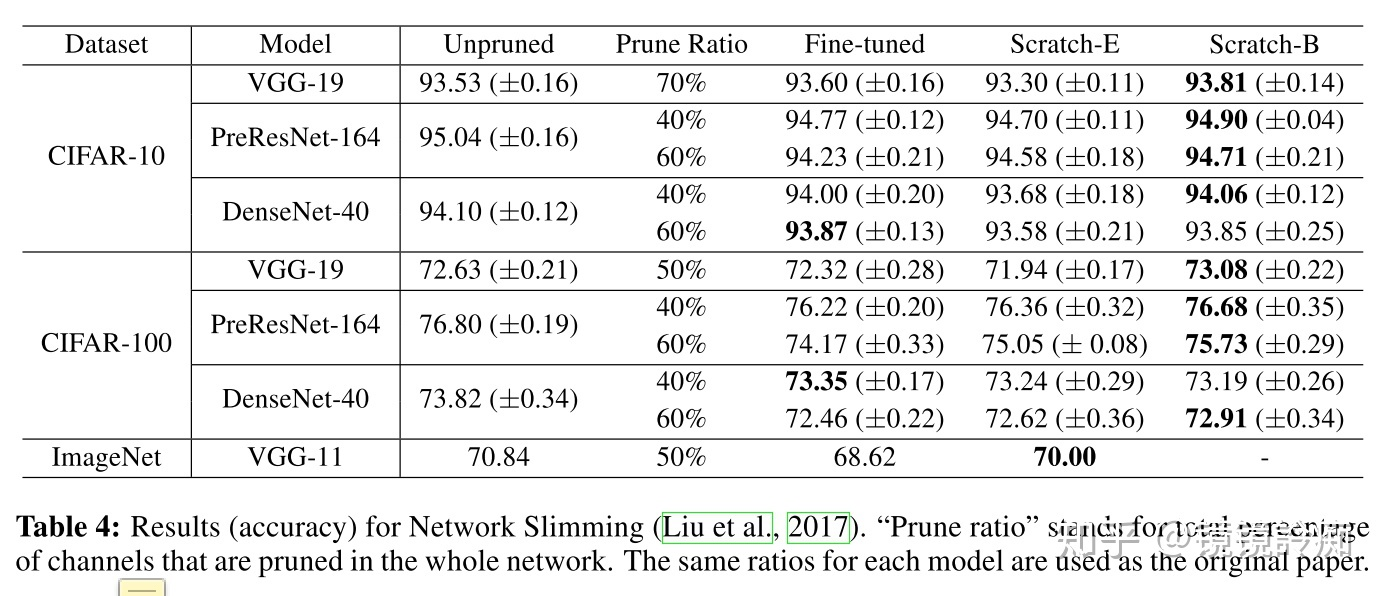
Where's the contradiction?

Rethink vals

Lottery Ticket

  • After choosing lottery ticket, we  get "good" architecture.
  • Random init can get high accuracy.
  • After choosing lottery ticket, we  get "good" weight initialization.
  • Random init will destroy the winning ticket.

So... what's the result? (1/2)

This conclusion is made in "lottery tickets".

\theta_0
\theta'_{fin}

after training

\theta'_0 \simeq \theta'_{fin}

lr must be small.

So... what's the result? (2/2)

This conclusion is made by "rethink vals" first author.

Winning ticket must be measured by "weight".

winning ticket helps unstructured pruning (e.g. weight pruning), but doesn't help structured pruning (e.g. filter/neuron pruning.)

So... what's the experience?

By "rethink vals" authors.

  1. In unstructured pruning (like pruning by weight), winning ticket can using small learning rate

Paper Reference

  • Knowledge Distillation

    • Distilling the Knowledge in a Neural Network (NIPS 2014)

    • Deep Mutual Learning (CVPR 2018)

    • Born Again Neural Networks (ICML 2018)

    • Label Refinery: Improving ImageNet Classification through Label Progression

    • Improved Knowledge Distillation via Teacher Assistant (AAAI 2020)

    • FitNets : Hints for Thin Deep Nets (ICLR2015)

    • Paying More Attention to Attention: Improving the Performance of Convolutional Neural Networks via Attention Transfer (ICLR 2017)

    • Relational Knowledge Distillation (CVPR 2019)

    • Similarity-Preserving Knowledge Distillation (ICCV 2019)

Paper Reference

  • Network Pruning

    • Pruning Filters for Efficient ConvNets (ICLR 2017)

    • Learning Efficient Convolutional Networks Through Network Slimming (ICCV 2017)

    • Filter Pruning via Geometric Median for Deep Convolutional Neural Networks Acceleration (CVPR 2019)
    • Network Trimming: A Data-Driven Neuron Pruning Approach towards Efficient Deep Architectures
    • The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks (ICLR 2019)
    • Rethinking the value of network pruning (ICLR 2019)

    • Deconstructing Lottery Tickets: Zeros, Signs, and the Supermask (ICML 2019)

Intro to Model Compression

By Arvin Liu

Made with Slides.com

Intro to Model Compression

ML2020 Spring Lecture

  • 8,080

More from Arvin Liu

  • Training Course - Knowledge Distillation
    Arvin Liu
    1224
  • Paper review: Revisiting Knowledge Distillation: An Inheritance and Exploration Framework (CVPR'21)
    Arvin Liu
    921