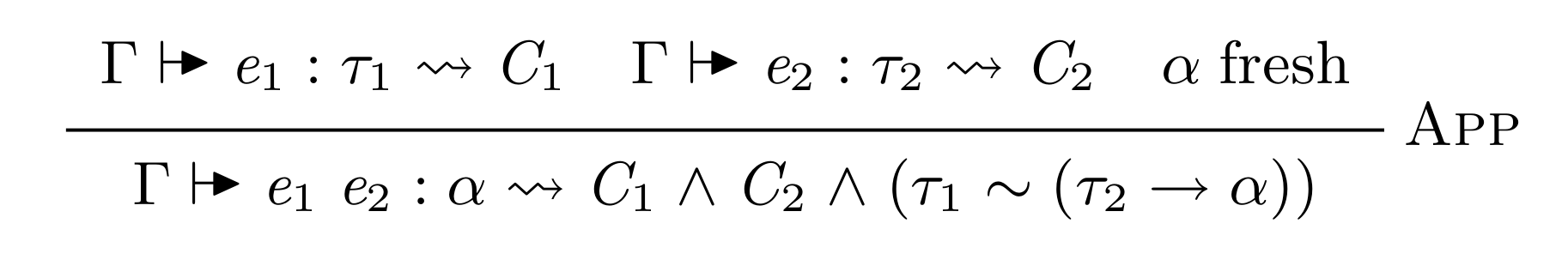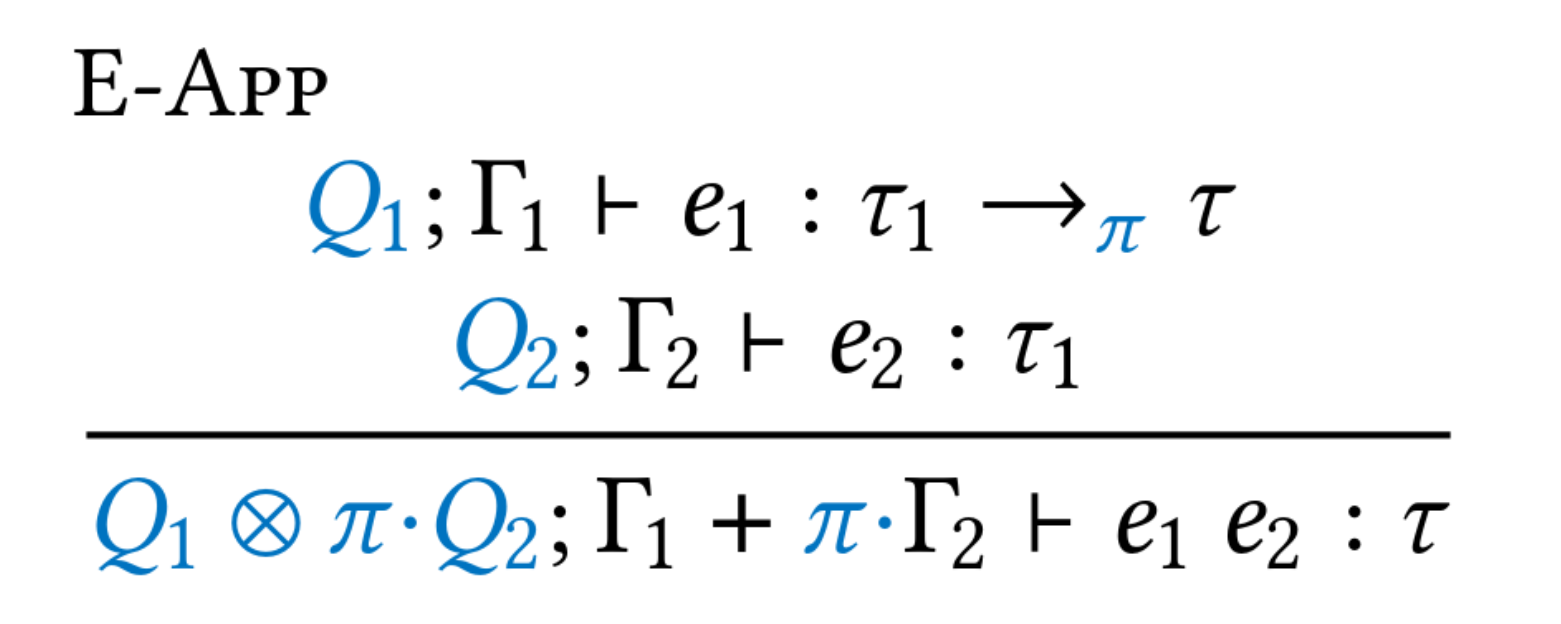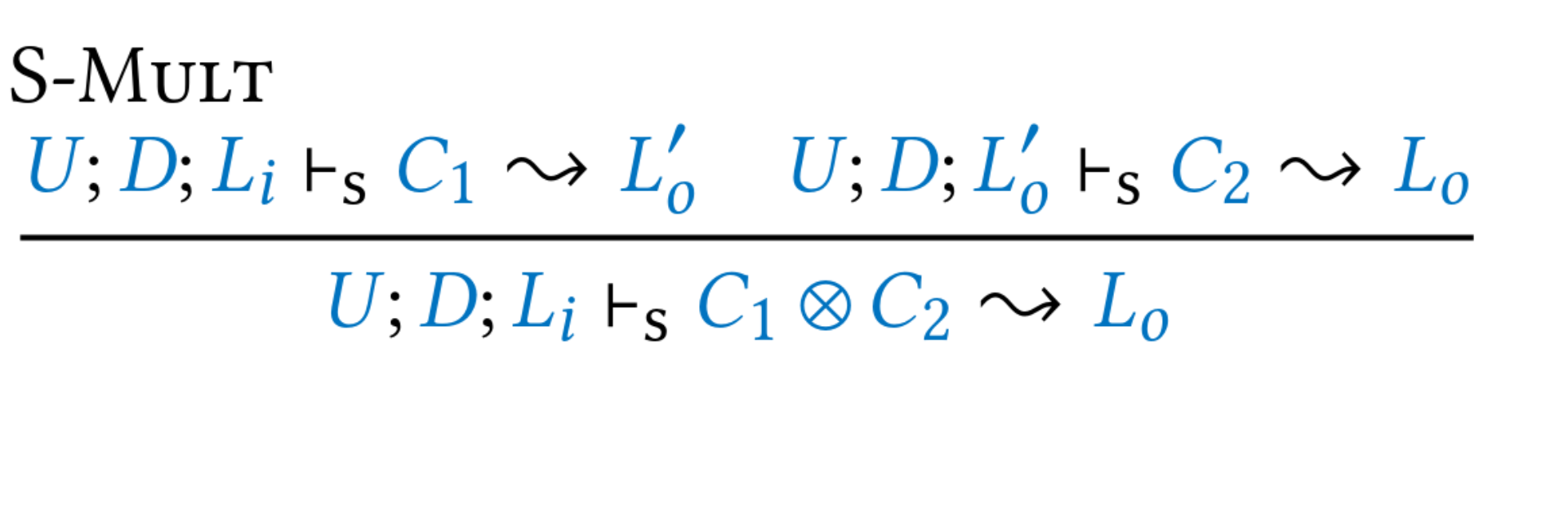Linearly Qualified Types

Arnaud Spiwack, Csongor Kiss,

Jean-Philippe Bernardy, Nicolas Wu,

Richard A. Eisenberg

Generic Inference for Capabilities and Uniqueness

Linear Haskell

Design sketch
2017

2018

POPL paper

Merged in GHC
2020

2021

GHC 9.0.1 released

Today
2022

Linear Haskell 101

A -> B
A %1 -> B

(plus polymorphism stuff, but not for today)

Regular function

Linear function

If the result is consumed exactly once, the argument is consumed exactly once

Pure mutable arrays

swap :: Int -> Int -> MArray a %1 -> MArray A
swap i j as =
  let
    !(as', Ur ai) = get i as
    !(as'', Ur aj) = get j as'
    as''' = set i aj as''
    as'''' = set j ai as'''
  in
  as''''
val swap : [a] duplicable a
    => (i: int, j: int, as: marray a) -> () =
  let ai = get (as, i) in
  let aj = get (as, j) in
  set (as, i, aj);
  set (as, j, ai)

Mezzo

Haskell

The design and formalization of Mezzo, a permission-based programming – Thibaut Balabonski, François Pottier, Jonathan Protzenko

Constraints

nub :: Eq a => [a] -> [a]

Constraints

OutsideIn(X) — Dimitrios Vytiniotis, Simon Peyton Jones, Tom Schrijvers, Martin Sulzmann

Linear Constraint

set :: RW n %1 => Int -> a -> MArra…
swap :: RW n %1 => Int -> Int -> MArray n a -> () ⧀ RW n
swap i j as =
  let
    !Ur ai = get i as
    !Ur aj = get j as
    !() = set i aj as
    !() = set j ai as
  in
  ()

Scope functions

newMArray :: Int -> (MArray a %1 -> Ur b) %1 -> Ur b
fromList :: [a] -> Array a
fromList as =
  unUr $ newMArray (length as) $ \arr ->
    let arr' = foldr (uncurry set) (zip [1..] as) arr in
    freeze arr'

tweag/linear-base#130: sources of uniqueness

Linearly constraint

newMArray :: Linearly %1 => Int -> MArray a
fromList :: Linearly %1 => [a] -> Array a
fromList as =
  let arr = newArray (length as) in
  let arr' = foldr (uncurry set) (zip [1..] as) arr in
  unUr $ freeze arr'

tweag/linear-base#130

Draw the rest of the owl

+

Declarative system

Constraint generation

Constraint solving

Inferred as

soundness

OutsideIn(X) — Dimitrios Vytiniotis, Simon Peyton Jones, Tom Schrijvers, Martin Sulzmann

https://slides.com/aspiwack/icfp2022

https://www.tweag.io/blog/tags/linear-types/

https://dl.acm.org/doi/10.1145/3547626

Linearly Qualified Types

By Arnaud Spiwack

Made with Slides.com

Linearly Qualified Types

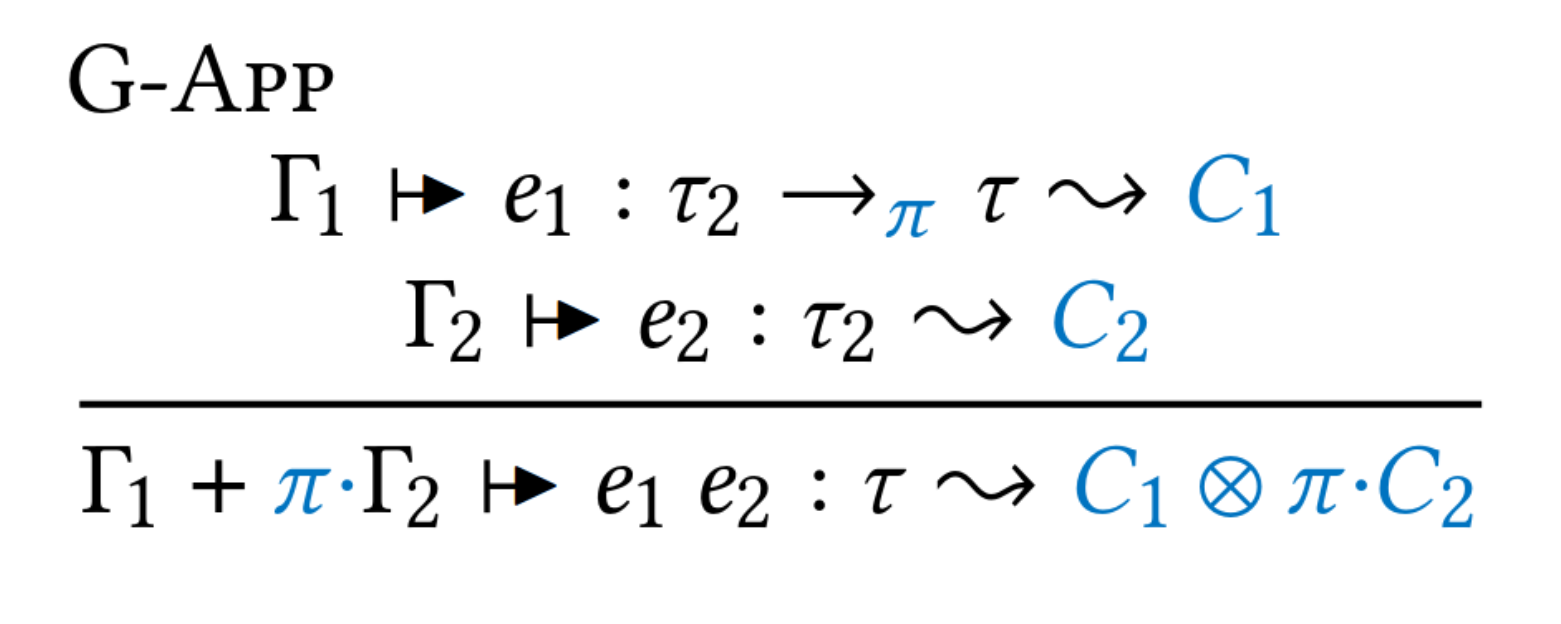
A linear parameter must be consumed exactly once in the body of its function. When declaring resources such as file handles and manually managed memory as linear arguments, a linear type system can verify that these resources are used safely. However, writing code with explicit linear arguments requires bureaucracy. This paper presents linear constraints, a front-end feature for linear typing that decreases the bureaucracy of working with linear types. Linear constraints are implicit linear arguments that are filled in automatically by the compiler. We present linear constraints as a qualified type system,together with an inference algorithm which extends GHC's existing constraint solver algorithm. Soundness of linear constraints is ensured by the fact that they desugar into Linear Haskell.

  • 414

More from Arnaud Spiwack