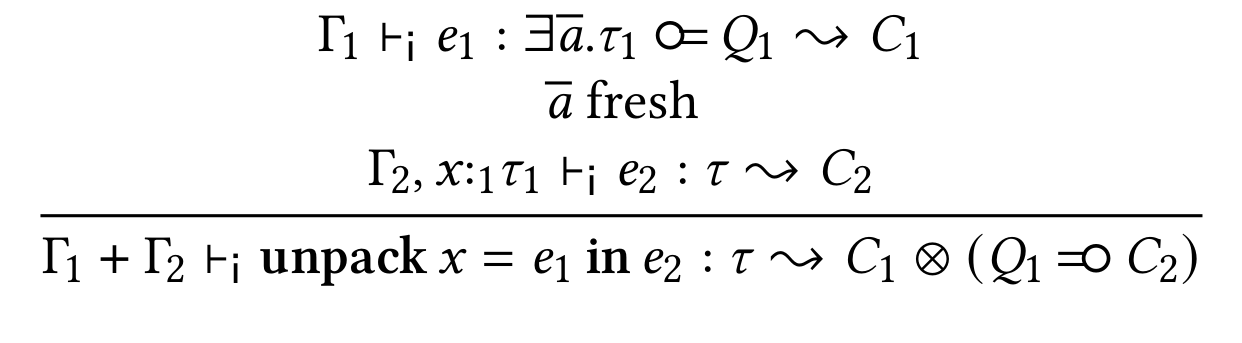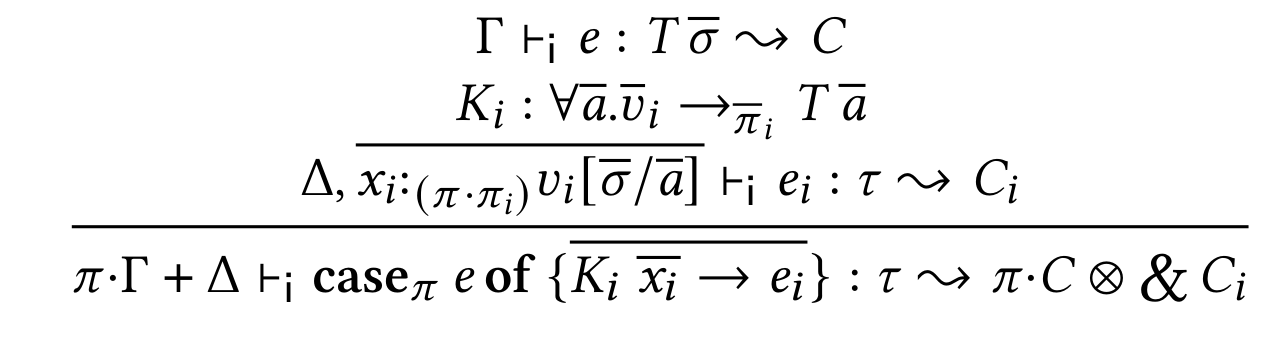Linear constraints

Arnaud Spiwack

Joint with: Jean-Philippe Bernardy, Richard Eisenberg, Csongor Kiss, Ryan Newton, Simon Peyton Jones, Nicolas Wu

Prolific literature…

… but not much delivery

That's about it

… until GHC 9.0

GHC 9.0.1 User's Guide

Linear Haskell

 a ⊸ b

Since GHC 9.0

{-# LANGUAGE LinearTypes #-}

Completely normal Haskell + an extra type

(+ stuff for polymorphism)

(but we won't talk about it today)

Consume exactly once

f :: A ⊸ B

Linear Haskell — Jean-Philippe Bernardy, Richard Newton, Simon Peyton Jones, Arnaud Spiwack

 f u
 u

If            is consumed exactly once
then      is consumed exactly once

What does “consume exactly once” mean?

evaluate x

apply x and consume the result exactly once

decompose x and consume both components exactly once

Base type

Function

Pair

The creative step

f :: A ⊸ A ⊸ !Int ⊸ B
g :: !B ⊸ C

h :: !A ⊸ C
h (!x) = g (!(f x x (!42)))
f :: A -> A -> Int -> B
g :: B -> C

h :: A -> C
h x = g (f x x (42))

vs

Linear types seem to require deep changes to the language

(e.g. Rust)

Linear types, by examples (1/3)

id x = x

✓

linear

dup x = (x,x)

✗

not linear

swap (x,y) = (y,x)

✓

linear

forget x = ()

✗

not linear

Linear types, by examples (2/3)

f (Left x) = x
f (Right y) = y

✓

linear

✓

linear

✗

not linear

h x b = case b of
  True -> x
  False -> x
g z = case z of
  Left x -> x
  Right y -> y
k x b = case b of
  True -> x
  False -> ()

✓

linear

Linear types, by examples (3/3)

f x = dup x

✓

linear

✗

not linear

h u = u 0
g x = id (id x)
k u = u (u 0)

✓

linear

✗

not linear

Application class 1

Making more things pure

Example: safe mutable arrays

Mutable arrays: the ST way

array :: Int -> [(Int,a)] -> Array a
array size pairs = runST $ do
  fma <- newMArray size
  forM pairs (write ma)
  return (unsafeFreeze ma)
newMArray    :: Int -> ST s (MArray s a)
read         :: MArray s a -> Int -> ST s a
write        :: MArray s a -> (Int, a) -> ST s ()
unsafeFreeze :: MArray s a -> ST s (Array a)
forM         :: Monad m => [a] -> (a -> m ()) -> m ()
runST        :: (∀s. ST s a) -> a

Allocate

Fill

Freeze

 unsafeFreeze

                      is unsafe!

The same, in Linear Haskell

array :: Int -> [(Int,a)] -> Array a
array size pairs = newMArray size $ \ma ->
  freeze (foldl write ma pairs)
newMArray :: Int -> (MArray a ⊸ Ur b) ⊸ Ur b
write     :: MArray a ⊸ (Int,a) -> MArray a
read      :: MArray a ⊸ Int -> (MArray a, Ur a)
freeze    :: MArray a ⊸ Ur (Array a)
foldl     :: (a ⊸ b ⊸ a) -> a ⊸ [b] ⊸ a

Allocate

Fill

Freeze (safe!)

See Data.Array.Mutable.Linear in linear-base

Threading style

write :: MArray a ⊸ (Int,a) -> MArray a

Can't do

write ma (1, True); write ma (2, False); …

Each write returns a new array

Scope passing style

newMArray :: Int -> (MArray a ⊸ Ur b) ⊸ Ur b

This is what ensures that references to arrays are unique

Unrestricted

data Ur a where
  Ur :: a -> Ur a

compare with

data Id a where
  Id :: a ⊸ Id a

Data types are linear by default

Scope passing style (continued)

newMArray :: Int -> (MArray a ⊸ Ur b) ⊸ Ur b

Don't work:

newMArrayDirect :: Int ⊸ MArray a
newMArrayLeaky :: Int -> (MArray a ⊸ b) ⊸ b

If the result is consumed exactly once
then the argument is consumed exactly once

Remember

Application class 2

Protocols in types

Example: files

I/O protocols

Files

  • ensure you close a file
  • ensure no read after close

Malloc

  • ensure you free a block
  • ensure no read after close

Sockets

  • ensure bind a socket before reading from it
  • ensure you close it
  • ensure you don’t read or bind after close

Files

openFile  :: FilePath -> IOL Handle
readLine  :: Handle ⊸ IOL (Handle, Ur String)
closeFile :: Handle ⊸ IOL ()
firstLine :: FilePath -> IOL (Ur String)
firstLine fp = do
  h <- openFile fp
  (h, Ur xs) <- readLine h
  closeFile h
  return $ Ur xs

Monads already have scope

do { x <- u ; v} = u >>= \x -> v
(>>=) :: IOL a ⊸ (a ⊸ IOL b) ⊸ IOL b

About the type of monads see A Tale of Two Functors or: How I learned to Stop Worrying and Love Data and Control — Arnaud Spiwack

Linear constraints

Coming back to files

openFile  :: FilePath -> IOL Handle
readLine  :: Handle ⊸ IOL (Handle, Ur String)
closeFile :: Handle ⊸ IOL ()
firstLine :: FilePath -> IOL (Ur String)
firstLine fp = do
  h <- openFile fp
  (h, Ur xs) <- readLine h
  closeFile h
  return $ Ur xs

The same 🙁

(Inter)Mezzo

Programming with permissions in Mezzo — François Pottier, Jonathan Protzenko

Doesn't return a new copy of ys

Constraints

show :: Show a => a -> String

A constraint

Prolog-like language

Constrained

With paramodulation

Idea: teach constraints linear logic

Files with linear constraints

Linear Constraints — Jean-Philippe Bernardy, Richard Eisenberg, Csongor Kiss, Arnaud Spiwack, Nicolas Wu

openFile  :: FilePath -> IOL (exists h. Ur (Handle h) <=%1 Open h)
readLine  :: Open h %1=> Handle -> IOL (Ur String)
closeFile :: Open h %1=> Handle -> IOL ()
firstLine :: FilePath -> IOL (Ur String)
firstLine fp = do
  Pack! h <- openFile fp
  Pack! xs <- readLine h
  closeFile h
  return $ Ur xs

Constraint generation

Constraints are generated (as in GHC)

in a linear logic (new!)

C₂ to be proved under linear assumption Q₁

Constraint generation (case)

Additive conjunction

Constraint resolution

“Hereditary Harrop” fragment of Linear Logic

Logic Programming in a Fragment of Intuitionistic Linear Logic — Joshua Hodas and Dale Miller

Efficient resource management for linear logic proof search — Iliano Cervesato, Joshua Hodas, Frank Pfenning

Reduces non-determinism to one rule

↳ add a strategy (“guess free”)

Will support current extension (“quantified constraints”)

Notion: uniform proof

↳ Originally: completeness of goal-oriented search

↳ For Linear Constraints: soundness(!!) of constraint generation

https://slides.com/aspiwack/lix202103

https://www.tweag.io/blog/tags/linear-types/

\chi

https://arxiv.org/abs/2103.06127

Linear Constraints

By Arnaud Spiwack

Made with Slides.com

Linear Constraints

In the past few years, I've been involved in extending the type system of the Haskell programming language to support linear types. In one sentence, a linear argument must be consumed exactly once in the body of its function; a linear function is a function whose argument is linear. Such a linear type system comes from linear logic (or, in this particular case, intuitionistic linear logic, but who's counting?) seen through the lens of the Curry-Howard correspondence. Linear typing has two main families of applications: making pure interface to mutable data structures, such as arrays (“pure” means that functions are functions in the sense of mathematics); and enforcing protocol in the type level, for instance making sure file handles are eventually closed and not written to after being closed. An example that combines both aspects is safe manual memory management, much in the style that the Rust programming language allows. This is all possible in the, latest, 9.0 release of GHC. However these applications, using GHC 9.0's linear types require quite a bit of additional syntactic bureaucracy, compared to their unsafe equivalent. In this talk, after introducing Haskell's linear types, I'll presents linear constraints, a front-end feature for linear typing that decreases the bureaucracy of working with linear types. Linear constraints are implicit linear arguments that are to be filled in automatically by the compiler. Linear constraints are presented as a qualified type system, together with an inference algorithm which extends OutsideIn, GHC's existing constraint solver algorithm. Soundness of linear constraints is ensured by the fact that they desugar into Linear Haskell.

  • 732

More from Arnaud Spiwack