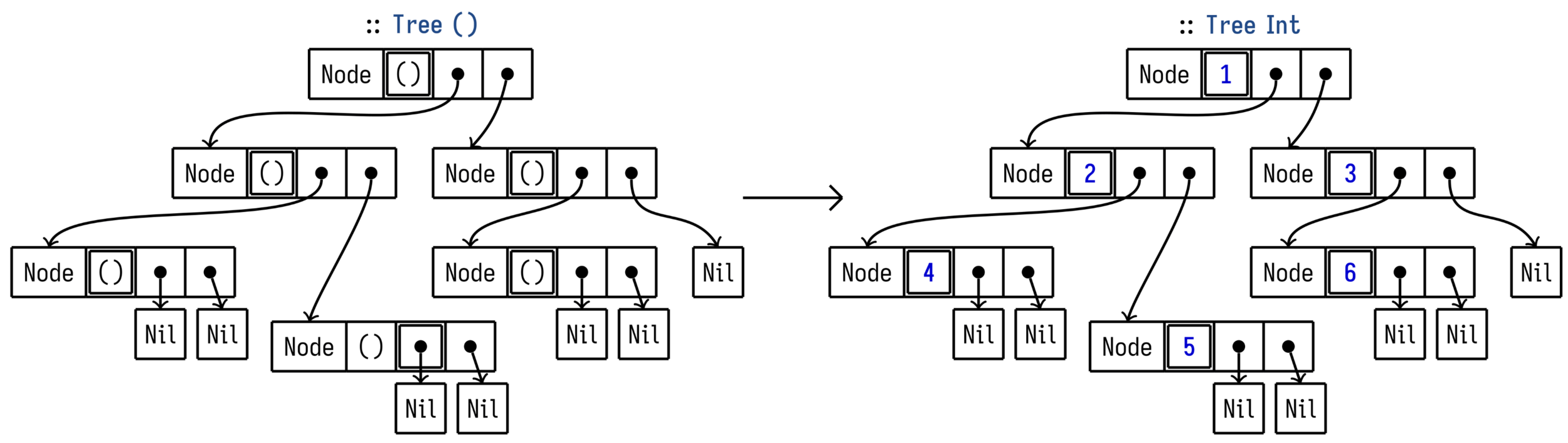
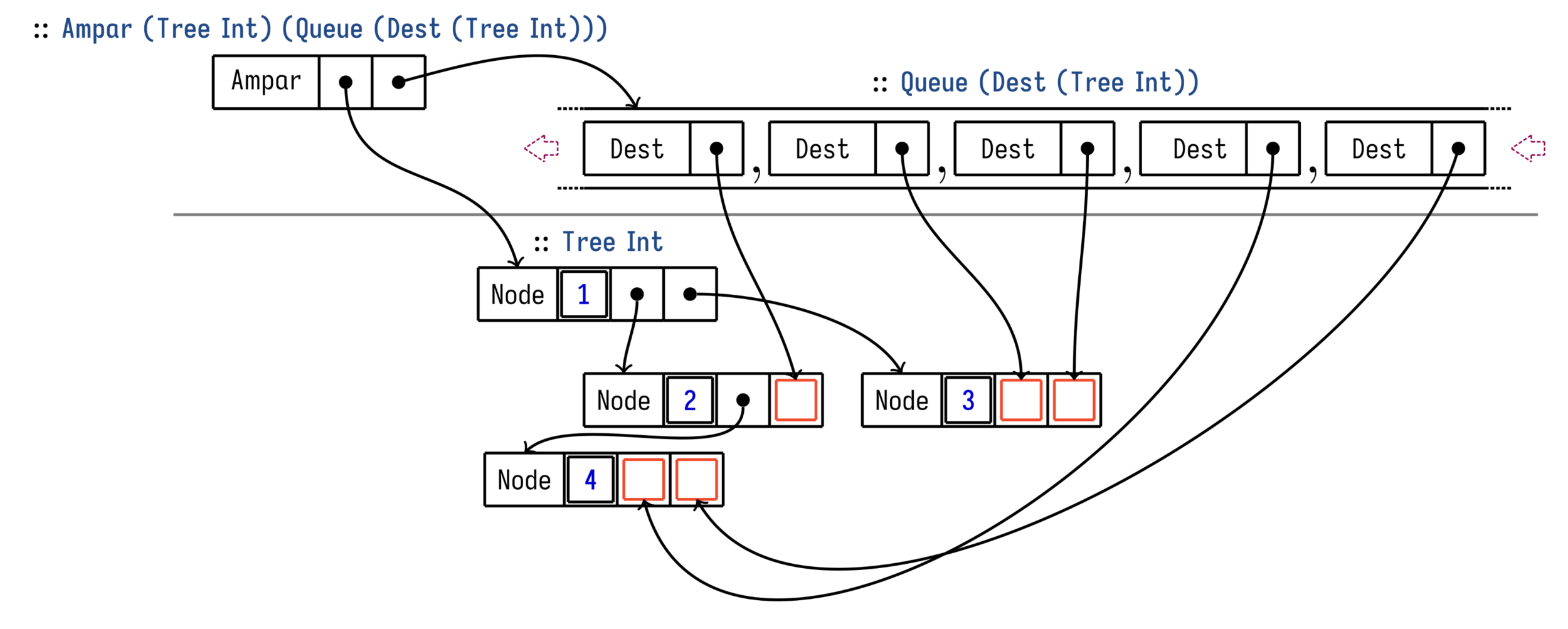
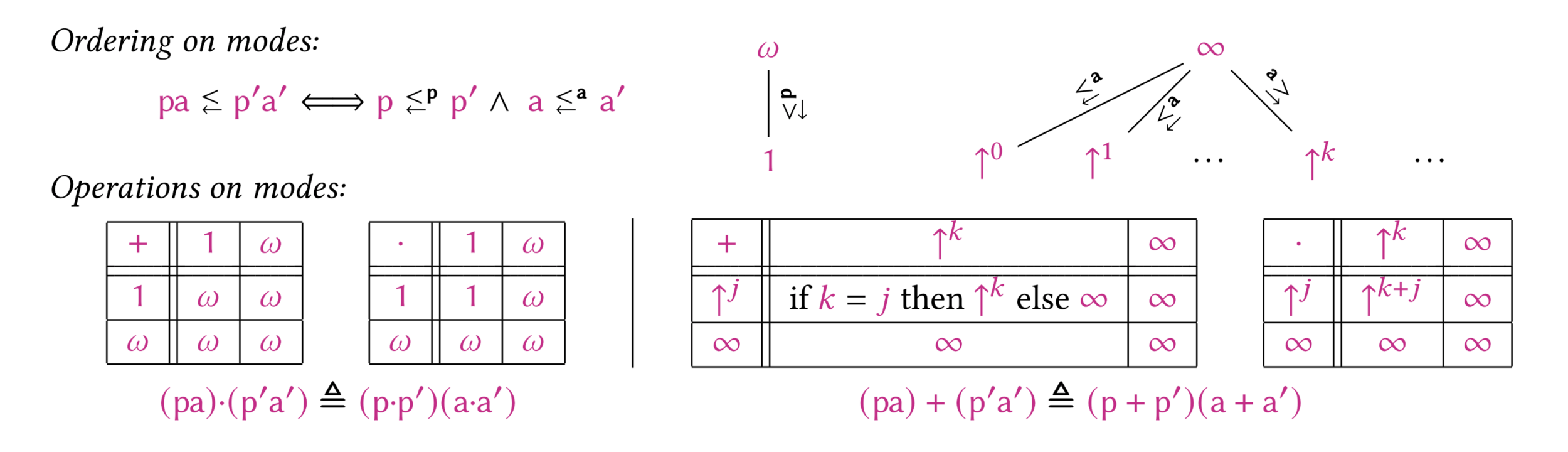
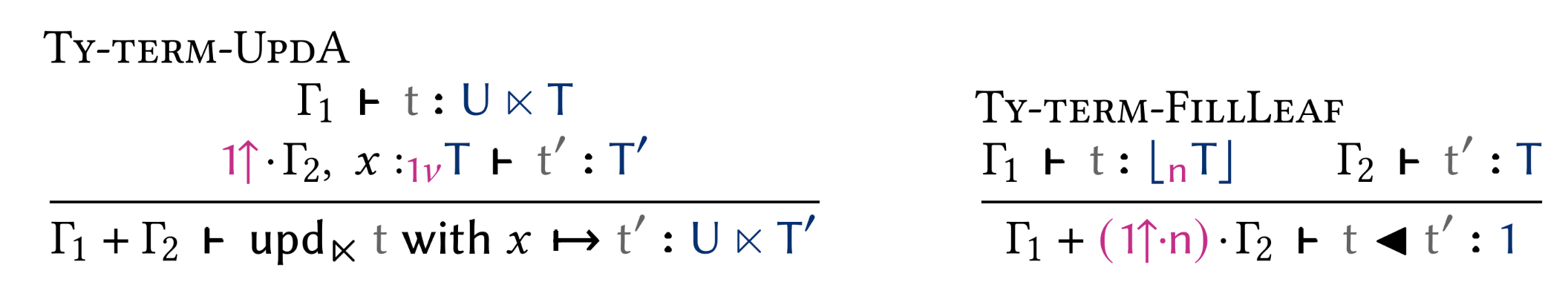Destination calculus

Thomas Bagrel & Arnaud Spiwack

A linear λ-calculus for purely functional memory writes

Map isn't tail recursive

let rec map f = function
  | [] -> []
  | a::l -> (f a) :: (map f l)
let mapk f l =
  let rec mapk k = function
    | [] -> k []
    | a::l -> map (fun l' -> (f a) :: l') l
  in
  mapk (fun l' -> l') l
let mapr f l =
  let rec rev acc = function
    | [] -> acc
    | a::l -> rev (a::acc) l
  and mapr acc = function
    | [] -> rev [] acc
    | a::l -> rev_map ((f a) :: acc) l
  in
  mapr [] l

😱

Solutions?

Tail recursion with one pass and mutation

type 'a mlist =
  | Nil
  | Cons of 'a * 'a mlist ref

let mapm f =
  let rec mapm (h,r) = function
    | Nil -> (r := Nil; !h)
    | Cons (a, l) -> begin
       let r' := ref Nil in
       r := (a :: r');
       mapm (h, r') !l
    end
  in
  let r := ref Nil in
  mapm (r, r)

Tail recursion modulo constructor

let[@tail_mod_cons]
  rec map f = function
  | [] -> []
  | a::l -> (f a) :: (map f l)
let mapm f =
  let rec mapm (h,r) = function
    | Nil -> (r := Nil; !h)
    | Cons (a, l) -> begin
       let r' := ref [] in
       r := (a :: r');
       mapm (h, r') !l
    end
  in
  let r := ref [] in
  mapm (r, r)

compiler
magic

Tail Modulo Cons –  Frédéric Bour, Basile Clément, Gabriel Scherer

Linear one-hole contexts

let mapm f =
  let rec mapm (h,r) = function
    | Nil -> (r := Nil; !h)
    | Cons (a, l) -> begin
       let r' := ref Nil in
       r := (a :: r');
       mapm (h, r') !l
    end
  in
  let r := ref Nil in
  mapm (r, r)

interp

let mapk f l =
  let rec mapk k = function
    | [] -> k []
    | a::l -> map (fun l' -> (f a) :: l') l
  in
  mapk (fun l' -> l') l

Linear

Linear
no pattern-match

\alpha\hat{\multimap}\beta

A functional representation of data structures with a hole – Yasuhiko Minamide

The Functional Essence of Imperative Binary Search Trees – Anton Lorenzen, Daan Leijen, Wouter Swierstra, and Sam Lindley

Breadth-first traversal

Destinations

\alpha\mathop{\hat{\multimap}}\beta
\alpha\multimap\beta
\beta\multimap\alpha^\bot
\&
\beta\ltimes\lfloor\alpha\rfloor
= Ampar b (Dest a)

Breadth-first traversal with destinations

The linearity contract

\alpha\multimap\beta

When you evaluate

then you evaluate

But what if you put the argument in a Dest and make it 🪄 disappear?

A solution for the ages

https://slides.com/aspiwack/oopsla2025

https://www.tweag.io/blog/tags/linear-types/

https://dl.acm.org/doi/abs/10.1145/3720423

Ages are implicit in most typing rules

Only semiring operations

Ages where relevant

How to segfault (without ages)

let outer :: Ampar (Dest ()) ()
    outer = (newAmpar tok1) `updWith` \(dd :: Dest (Dest ())) →
              let inner :: Ampar () ()
                  inner = (newAmpar tok2) `updWith` \(d :: Dest ()) →
                            dd &fillLeaf d
               in fromAmpar' inner
 in fromAmpar' outer

Destination calculus

By Arnaud Spiwack

Destination calculus

Destination passing —aka. out parameters— is taking a parameter to fill rather than returning a result from a function. Due to its apparent imperative nature, destination passing has struggled to find its way to pure functional programming. In this paper, we present a pure core calculus with destinations. Our calculus subsumes all the similar systems, and can be used to reason about their correctness or extension. In addition, our calculus can express programs that were previously not known to be expressible in a pure language. This is guaranteed by a modal type system where modes are used to represent both linear types and a system of ages to manage scopes. Type safety of our core calculus was proved formally with the Coq proof assistant.

  • 2

More from Arnaud Spiwack