Упражнение 7*
§1. Подмногообразия в
\mathbb{R}^{N}
В качестве f выберем:
f = det A - 1
Распишем определитель:
det A = a_{11}detA_{11} + ... + (-1)^{n+1}a_{1n}detA_{1n}-1
Найдём чему равен , для этого запишем дифференциал преобразования:
rank f
df = \left ( \frac{\partial f}{\partial a_{11}}...\frac{\partial f}{\partial a_{nn}}\right )
1. Пусть , тогда:
A = I_{n}
\frac{\partial f}{\partial a_{11}} = \frac{\partial a_{11}detA_{11}}{\partial a_{11}} = detA_{11}
\frac{\partial f}{\partial a_{11}}(I_{n}) = 1
Значит .
rank f = 1
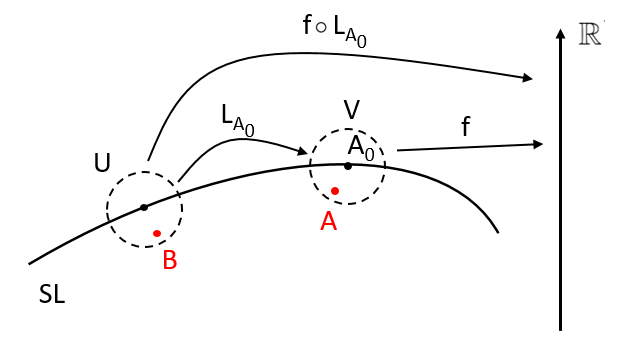
2. Рассмотрим
A_{0} \in SL(n,\mathbb{R})
B = \bigl(\begin{smallmatrix}
b_{11} & ... & b_{1n}\\
... & ... & ...\\
b_{n1}& ... &b_{nn}
\end{smallmatrix}\bigr)
B = A_{0}^{-1}A
Тогда:
f(A) = f(A\circ B) = det(A_{0})det(B) = f(B)
\frac{\partial f}{\partial b_{11}} = \sum_{ij} \frac{\partial f}{\partial a_{ij}}(A_{0}) \frac{\partial a_{ij}}{\partial b_{11}}
если , то и, следовательно, . Значит подмногообразие размерности .
B\overset{L_{A_{0}}}{\mapsto} A = A_{0}\cdot B
A = A_{0}
B = I_{n}
rank f = 1
SL(n,\mathbb{R})
n^{2}-1
§1. Упражнение 7*
By ASTepliakov
