On the Dynamics of HIV and Malaria Infection - Insights From Mathematical Models

Bernhard Paul Konrad

Mathematics

The University of British Columbia

4 September 2015

Overview

  1. Theory of branching processes
  2. Length of the eclipse phase for HIV
  3. Analysing Get Checked Online
  4. A fungus to fight malaria

Theory of Branching Processes

  • Most results known in some form, but have not been applied to HIV in this way

Consider the birth-death process

N \rightarrow N + 1
N→N+1N \rightarrow N + 1
N \rightarrow N - 1
N→N−1N \rightarrow N - 1
d
dd
b
bb

birth

death

Want:

P(n, n_0, t) = \text{Prob}(N(t)=n\,|\,N(0)=n_0)
P(n,n0,t)=Prob(N(t)=n∣N(0)=n0)P(n, n_0, t) = \text{Prob}(N(t)=n\,|\,N(0)=n_0)

Simple: Forward and backward master equation

Helper: The probability generating function

G(n_0, t, z) = E[z^N] = \displaystyle \sum_{n=0}^\infty P(n, n_0, t)z^n
G(n0,t,z)=E[zN]=∑n=0∞P(n,n0,t)znG(n_0, t, z) = E[z^N] = \displaystyle \sum_{n=0}^\infty P(n, n_0, t)z^n

Forward master equation leads to PDE

\frac{\partial G(n_0, t, z)}{\partial t} = (bz^2 + d - (b+d)z)\frac{\partial G(n_0, t, z)}{\partial z}
∂G(n0,t,z)∂t=(bz2+d−(b+d)z)∂G(n0,t,z)∂z\frac{\partial G(n_0, t, z)}{\partial t} = (bz^2 + d - (b+d)z)\frac{\partial G(n_0, t, z)}{\partial z}

Backward master equation and branching property lead to ODE

\frac{\partial G(1, t, z)}{\partial t} = bG^2(1, t, z) + d - (b+d)G(1, t, z)
∂G(1,t,z)∂t=bG2(1,t,z)+d−(b+d)G(1,t,z)\frac{\partial G(1, t, z)}{\partial t} = bG^2(1, t, z) + d - (b+d)G(1, t, z)

Probability generating function

P(n, n_0, t) = \left.\frac1{n!}\frac{\partial^n G(n_0, t, z)}{\partial z^n}\right|_{z = 0}
P(n,n0,t)=1n!∂nG(n0,t,z)∂zn∣z=0P(n, n_0, t) = \left.\frac1{n!}\frac{\partial^n G(n_0, t, z)}{\partial z^n}\right|_{z = 0}

Knowing pgf means know everything (also: moments)

= \frac1{\pi}\text{Re}\left(\int_0^\pi G(n_0, t, e^{i\varphi})e^{-in\varphi}\,d\varphi\right)
=1πRe(∫0πG(n0,t,eiφ)e−inφdφ)= \frac1{\pi}\text{Re}\left(\int_0^\pi G(n_0, t, e^{i\varphi})e^{-in\varphi}\,d\varphi\right)
E[N] = \displaystyle \sum_{n=0}^\infty nP(n, n_0, t) = \left.\frac{\partial G(n_0, t, z)}{\partial z}\right|_{z=1}
E[N]=∑n=0∞nP(n,n0,t)=∂G(n0,t,z)∂z∣z=1E[N] = \displaystyle \sum_{n=0}^\infty nP(n, n_0, t) = \left.\frac{\partial G(n_0, t, z)}{\partial z}\right|_{z=1}

Probability generating function

Conditioning on non-extinction

When fitting model to HIV data, exposures that did not lead to infection can be recorded. Does this bias matter?

Coin-flip intuition

Heads: +1.1 points

    Tails: - 1    point  

A) Start with 20 points

B) Start with    1  point  

Average "survivors" (> 0 points) only

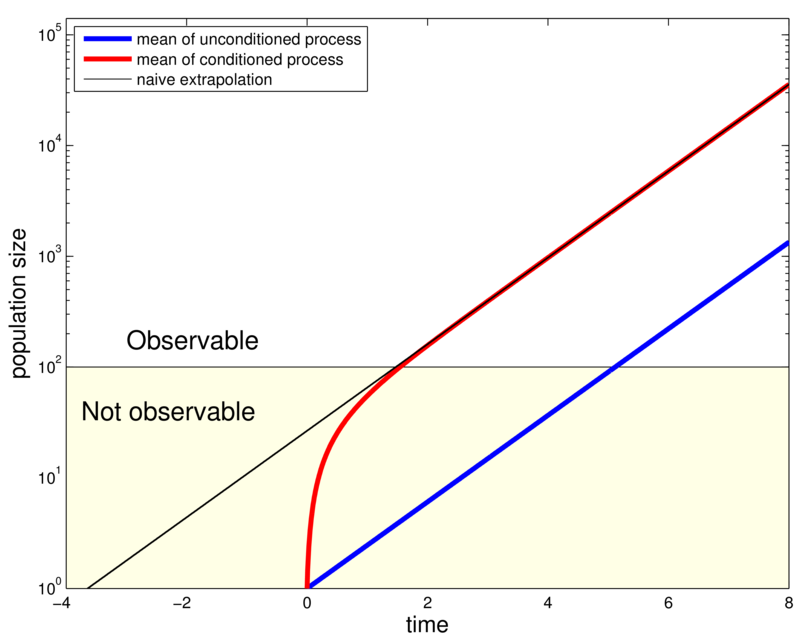
Fit conditioned process to match bias in the data! Using Bayes rule and the Markov property

\text{Prob}(N(t)=n\,|\,N(0)=n_0,\, \color{red}{N(\infty)\neq 0})
Prob(N(t)=n∣N(0)=n0,N(∞)≠0)\text{Prob}(N(t)=n\,|\,N(0)=n_0,\, \color{red}{N(\infty)\neq 0})
= \frac1{1-q^{n_0}}(P(n, n_0, t)-P(n, n_0, t)q^n)
=11−qn0(P(n,n0,t)−P(n,n0,t)qn)= \frac1{1-q^{n_0}}(P(n, n_0, t)-P(n, n_0, t)q^n)

So only a slight modification of the corresponding pgf is required.

Conditioning on non-extinction

Method naturally extends to multi-type processes.

Estimating the length of the eclipse phase

Clinical questions:

  1. How soon after exposure should I get tested for HIV infection?
  2. How reliable is an early negative result?
  3. When should I schedule a follow-up, confirmatory test?

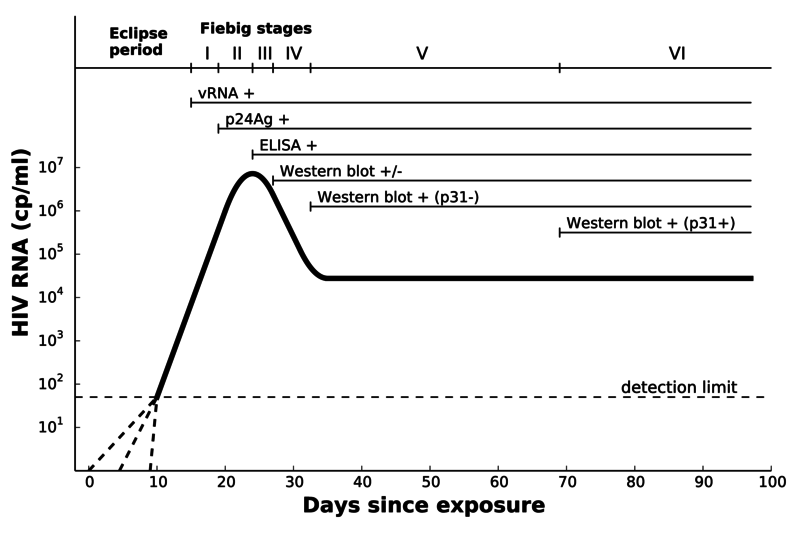
Data: seroconversion panels

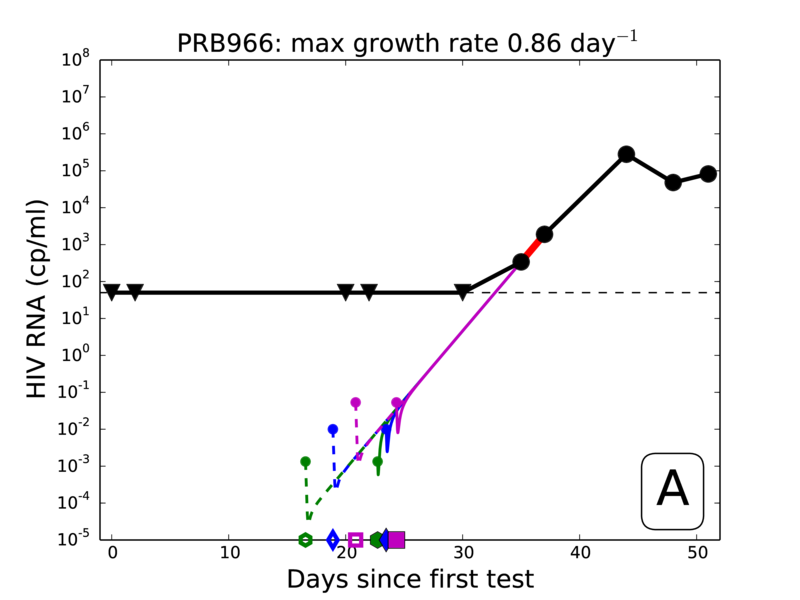
  • Viral load growth data obtained from historic seroconversion panels (plasma donors)
  • All donations removed from circulation if any sample tests positive
  • More sensitive tests today can detect HIV in early samples

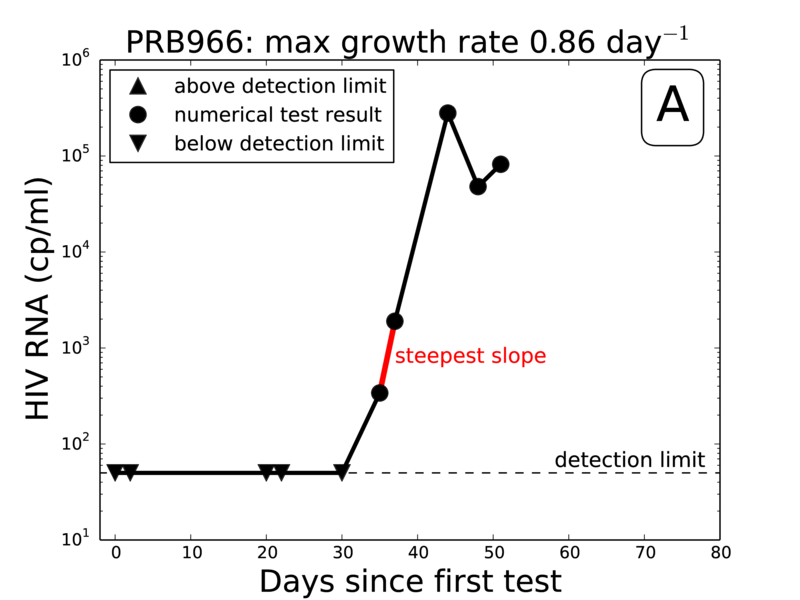
Extract steepest slope from each panel

Probability of false negative test

  • Compare unconditioned and conditioned model
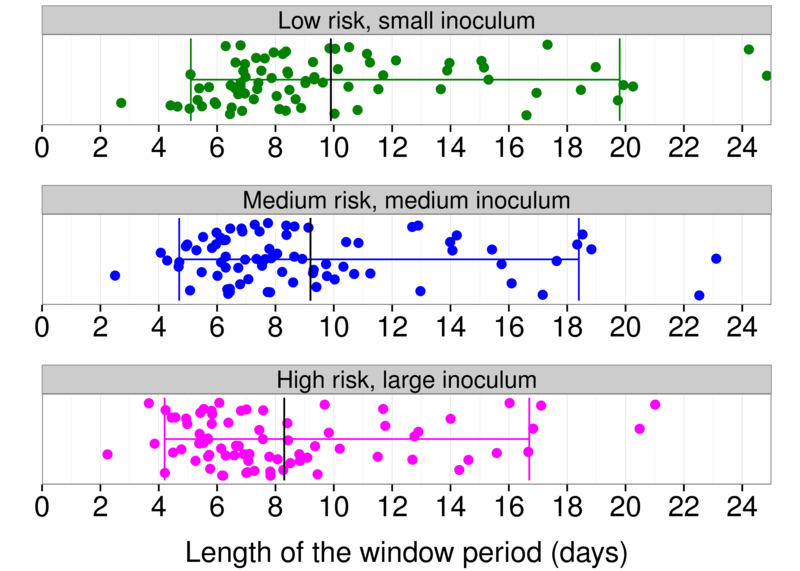
  • Conditioning reveals shorter eclipse phase
  • Consider different risk scenarios

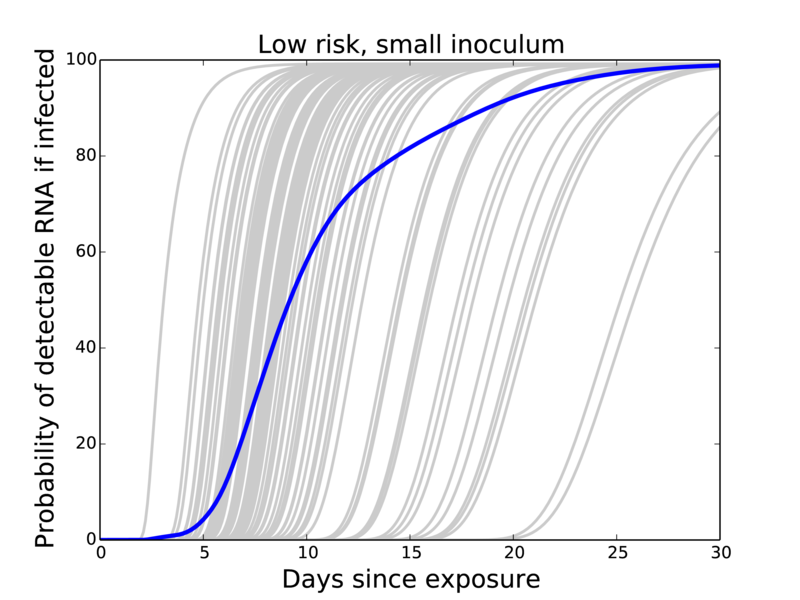
Have: Probability of negative test given infection

Want: Probability of infection given negative test

So use Bayes formula!

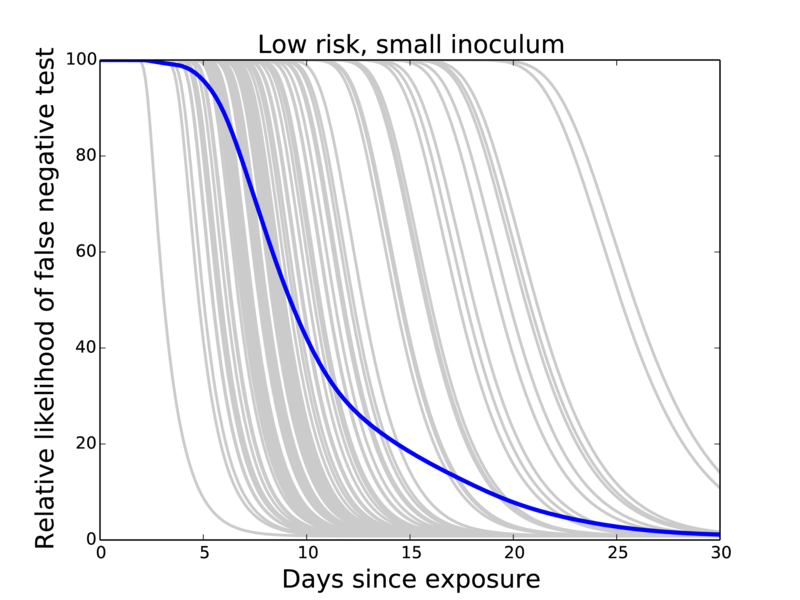
Probability of false negative test

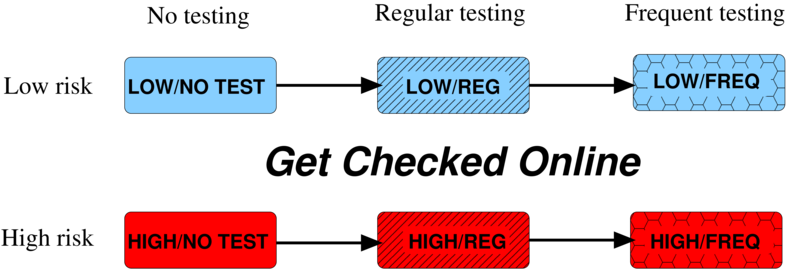
Get Checked Online

Collaboration with BCCDC to understand, predict and optimize impact of MSM-focused health program

HIV prevalence:

  • 0.2% in Canada
  • 15%   in Vancouver MSM

MSM = Men who have sex with men

BCCDC = British Columbia Centre for Disease Control

23% of young MSM under 30 never tested for HIV

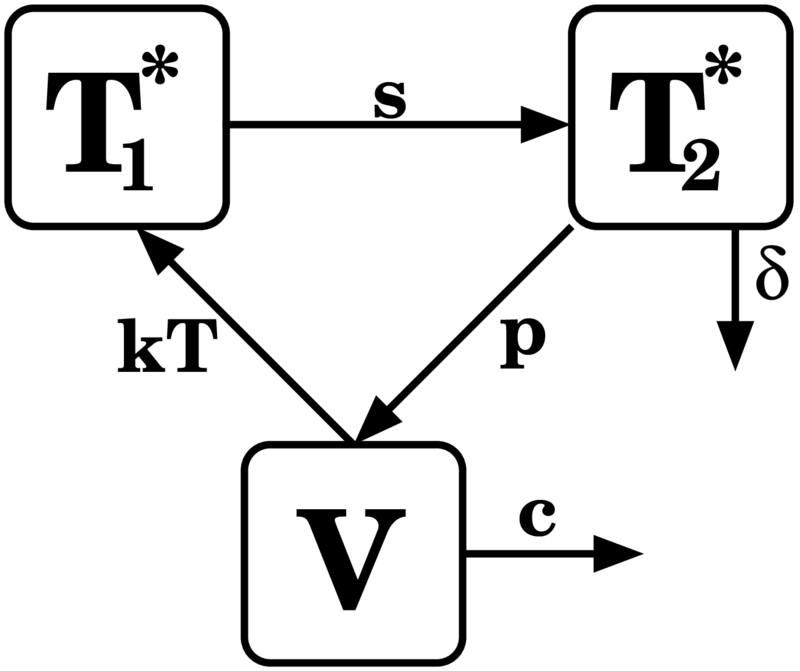
Basic Mathematical Model

  • Susceptible
  • Infected Unaware
  • Infected Aware
\frac{dS}{dt} = e(U + A) - S{\color{blue}r}\frac{\color{green}{p_U} U + \color{green}{p_A} A}{N}
dSdt=e(U+A)−SrpUU+pAAN\frac{dS}{dt} = e(U + A) - S{\color{blue}r}\frac{\color{green}{p_U} U + \color{green}{p_A} A}{N}
\frac{dU}{dt} = S{\color{blue} r}\frac{\color{green}{p_U} U + \color{green}{p_A} A}{N} - (e+{\color{red}\tau})U
dUdt=SrpUU+pAAN−(e+τ)U\frac{dU}{dt} = S{\color{blue} r}\frac{\color{green}{p_U} U + \color{green}{p_A} A}{N} - (e+{\color{red}\tau})U
\frac{dA}{dt} = {\color{red}\tau} U - eA
dAdt=τU−eA\frac{dA}{dt} = {\color{red}\tau} U - eA

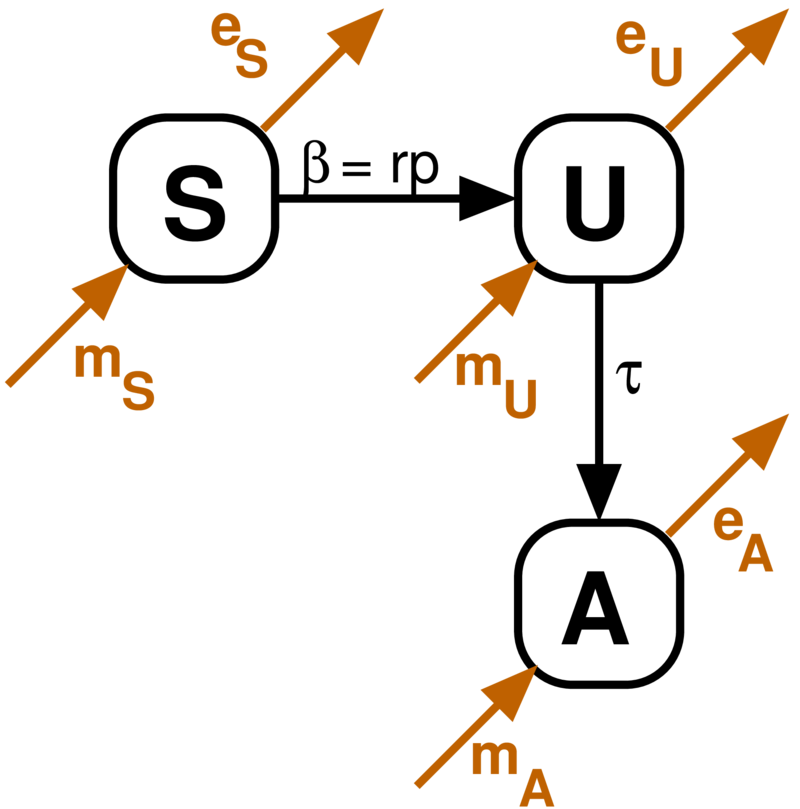
Main parameters to estimate:

  • r - rate of risky events
  • p - per-encounter risk
  •    - testing rate
\color{red}\tau
τ\color{red}\tau

Data and parameters

r - rate of risky events

p - per-encounter risk

    - testing rate

Two data sources (N = 166):

  1. Online surveys on, e.g.
    • HIV testing history
  2. Network grid interviews
    • recent partners, relationships
\color{red}\tau
τ\color{red}\tau

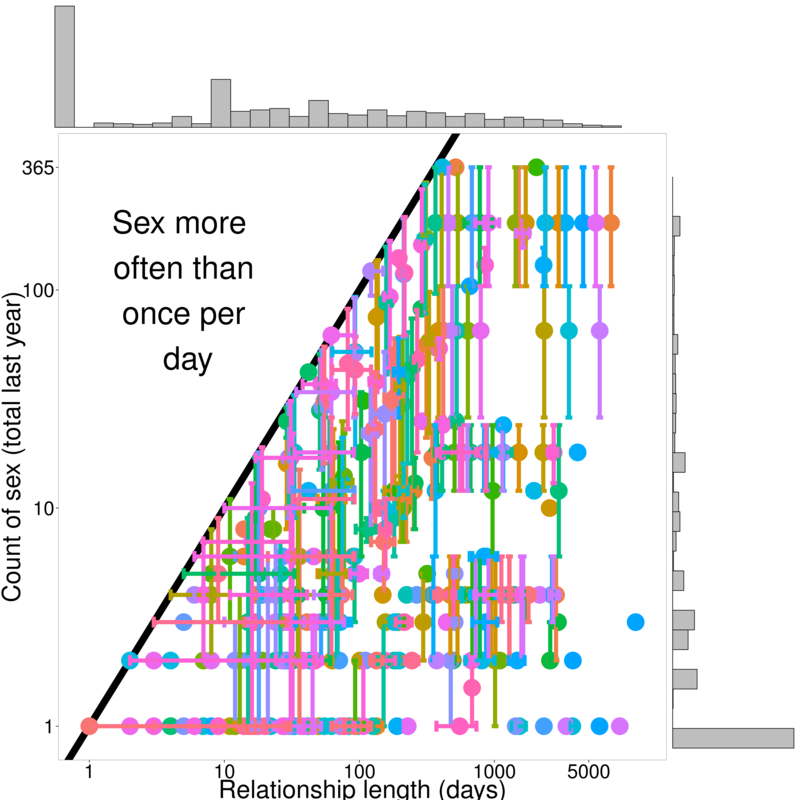
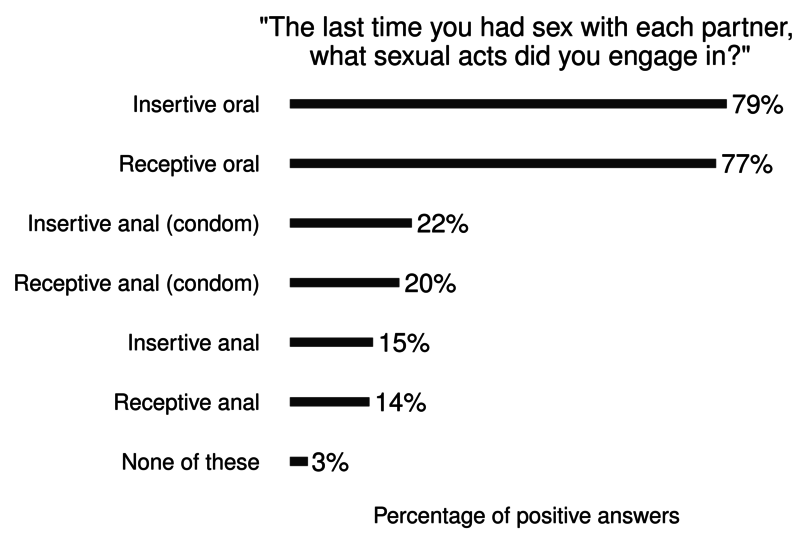
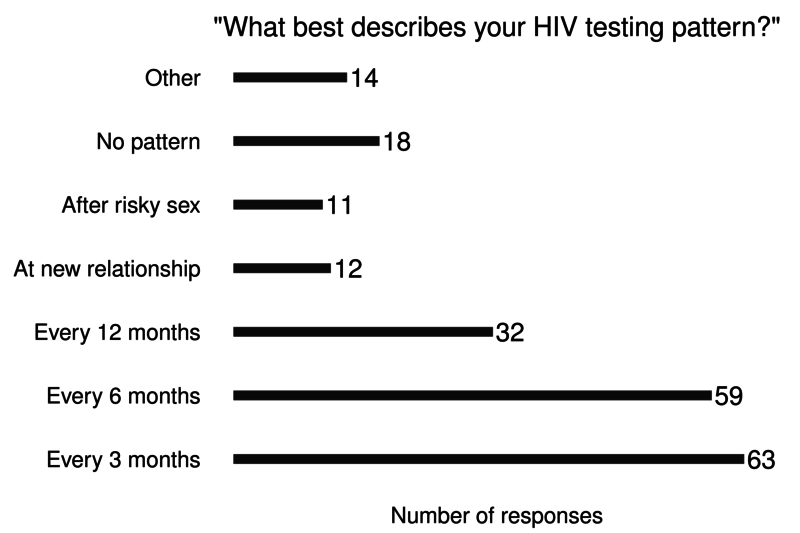
Additional: Sex Now 2011

Full model

  • 3 x 6 =  18 equations
  • Consider both extremes of contact mixing

Parameter estimation

  • Define testing groups from survey answers
  • Use Sex Now data to calculate transition rate from "no testing" to "regular testing"
\tau
τ\tau
\beta
β\beta
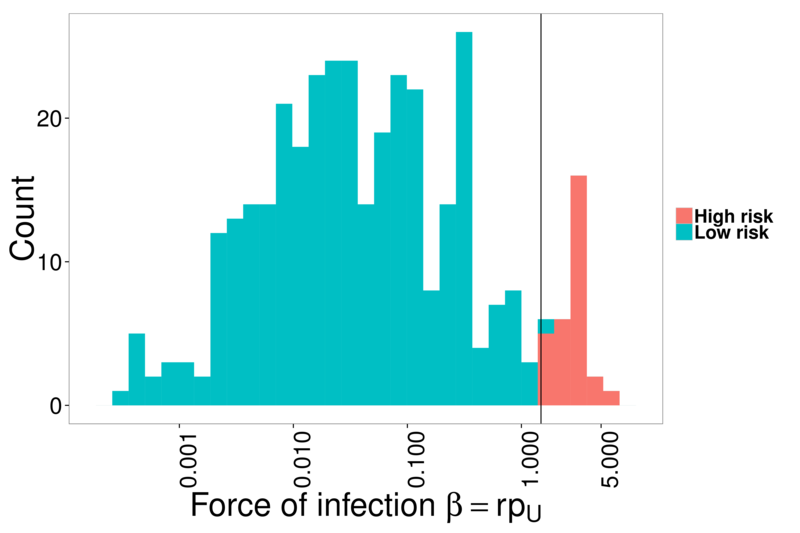
  • Calculate per-person force of infection
  • Use 2-means clustering to find cut-off (result: 8.3% high risk)

Results

BCCDC: 806 newly detected infections

Homogeneous 5 years projection Heterogeneous
2.73 R0 2.50
2314 New infections 1878
2063 Newly detected 1757
66.4 Averted infections 36.4

Core group effect

Future work:

  • Add partnerships
  • Include acute infection and treatment
  • Testing rate may depend on risk activity
  • Agent-based model

Malaria

  • Malaria endemic in 100 countries
  • Transmitted by mosquitoes
  • Traditional: Decrease mosquito count
  • Problem: Toxic, mosquito resistance
  • Recently proposed: Fungus that neutralizes malaria parasite in mosquito

Research question:

What is the optimal fungal virulence?

biopesticide effect vs. competition effect

Model and objective

\frac{dS}{dt} = \kappa(S+I+F)\color{red}{\left(1-\frac{S+I+F}{P}\right)}-\beta Sh - (\mu+\color{blue}\alpha)S
dSdt=κ(S+I+F)(1−S+I+FP)−βSh−(μ+α)S\frac{dS}{dt} = \kappa(S+I+F)\color{red}{\left(1-\frac{S+I+F}{P}\right)}-\beta Sh - (\mu+\color{blue}\alpha)S
\frac{dF}{dt} = \color{blue}{\alpha}(S+I) - (\mu + \color{green}{\sigma})F
dFdt=α(S+I)−(μ+σ)F\frac{dF}{dt} = \color{blue}{\alpha}(S+I) - (\mu + \color{green}{\sigma})F

Mosquito competition

Fungus spraying rate

Fungal virulence

Basic model

Goal: Minimize endemic prevalence in humans

h_e = \frac{R_0^2(\color{blue}\alpha, \color{green}\sigma)-1}{R_0^2(\color{blue}\alpha, \color{green}\sigma) + \beta/(\mu + \color{blue}\alpha)}
he=R02(α,σ)−1R02(α,σ)+β/(μ+α)h_e = \frac{R_0^2(\color{blue}\alpha, \color{green}\sigma)-1}{R_0^2(\color{blue}\alpha, \color{green}\sigma) + \beta/(\mu + \color{blue}\alpha)}

Results

Results:

  • Increasing fungus-spraying rate      decreases human malaria prevalence
  • There is a worst-case virulence
\color{blue}\alpha
α\color{blue}\alpha
\sigma^* = \frac{\kappa - 2\mu}{2-\kappa/(\mu+\alpha)}
σ∗=κ−2μ2−κ/(μ+α)\sigma^* = \frac{\kappa - 2\mu}{2-\kappa/(\mu+\alpha)}

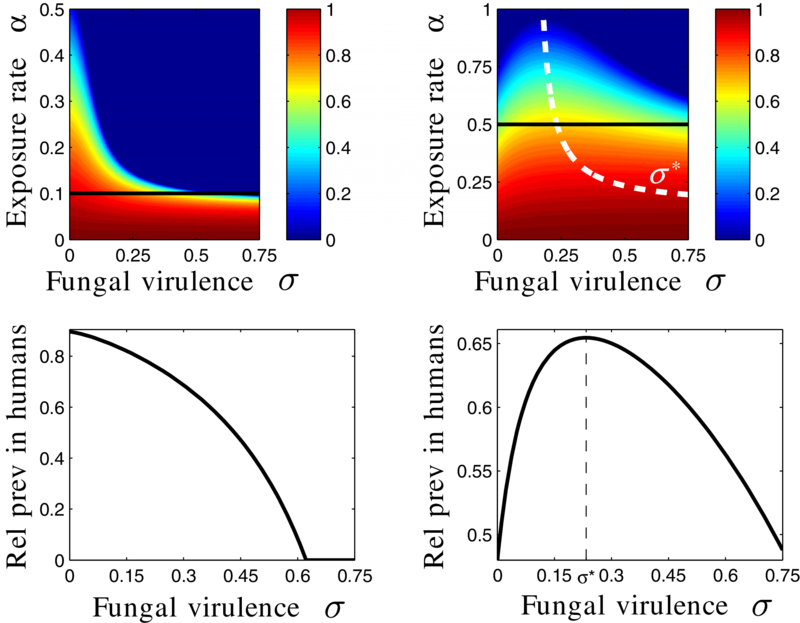
Life-structured model with with vertical transmission and competition in larvae stage

Vertical transmission

  • unlikely: choose high virulence
  • likely: choose low, but not too low virulence
\sigma^* < 0
σ∗<0\sigma^* < 0
\sigma^* > 0
σ∗>0\sigma^* > 0

Summary

Projects that show the usefulness of mathematical biology to reveal practical insights into current problems of global scale

  1. Derive theory of branching processes from first principles, focus on the application and numerical implementation
  2. Quantify uncertainty of early HIV tests and predict that eclipse phase may be shorter than previously assumed
  3. Estimate population-level impact of increased HIV testing and reveal core-group dynamics
  4. Optimize fungus characteristics to minimize human malaria prevalence

defence

By Bernhard Konrad

Made with Slides.com

defence

  • 522

More from Bernhard Konrad