Mathematical models to quantify and optimize HIV intervention in British Columbia
CMS Meeting Hamilton
2014-12-07
UBC: Bernhard Konrad, Daniel Coombs
BCCDC: Warren Michelow, Mark Gilbert



General background
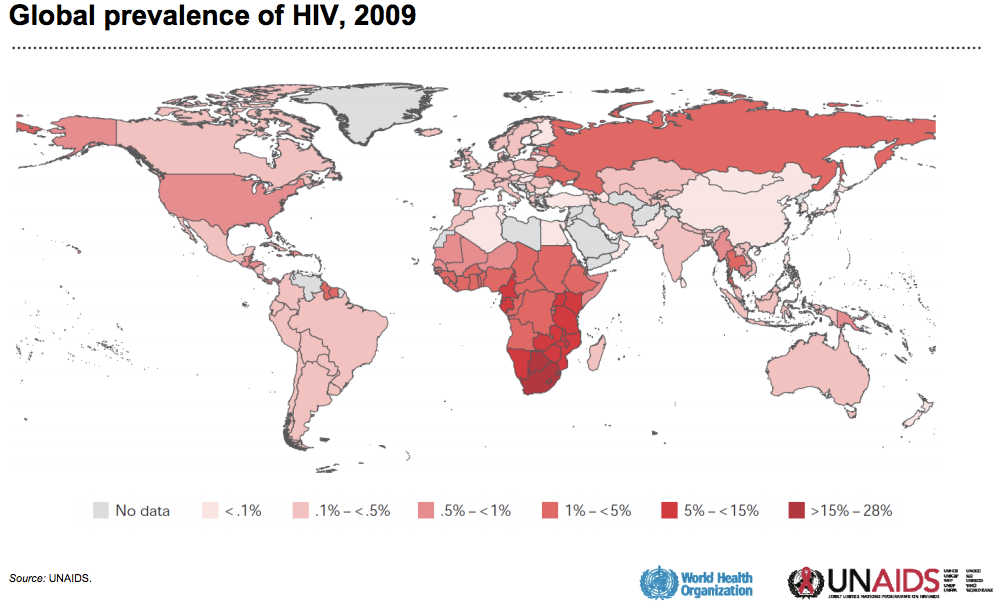
HIV in Canada
Canada
- 70,000 HIV+ (2009)
- 2,500 new diagnosis every year
- one new infection every 3h
BC
- 400 new diagnosis every year
- 3500 unaware of infection (25%)
Vancouver
- 6000 HIV+ (1.2%)
- 250 new diagnosis every year
- ~50% MSM, ~25% IDU, ~25% HET
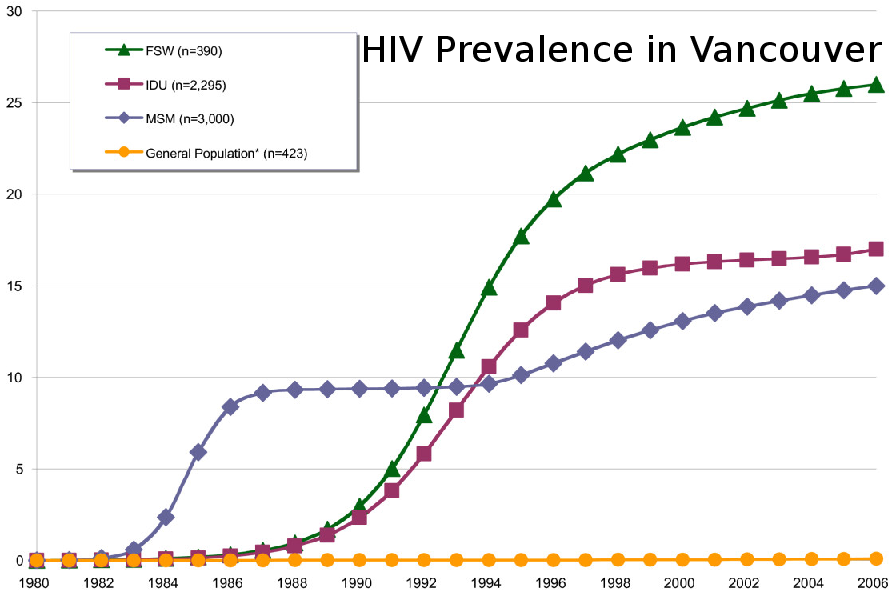
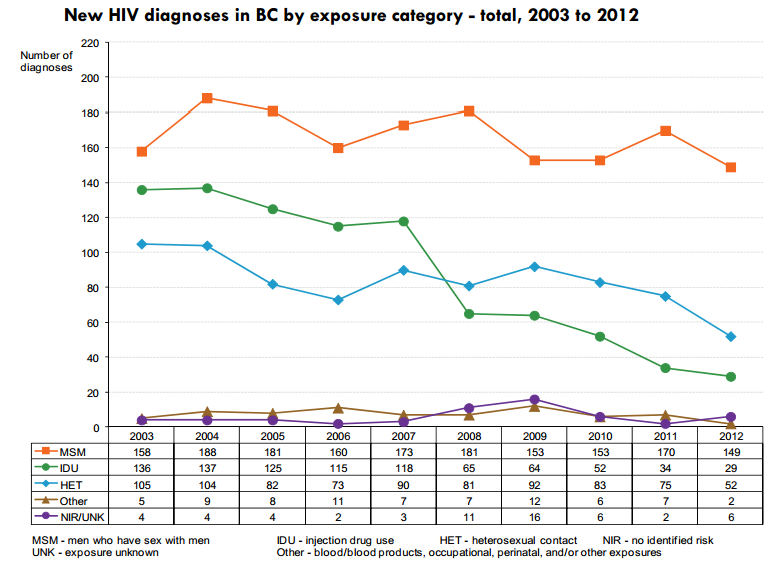
Goal: Understand the non-improvement for MSM
Modelling Epidemics

\frac{dS}{dt} = -\beta SI/N
dtdS=−βSI/N
\frac{dI}{dt} = \beta SI/N - \gamma I
dtdI=βSI/N−γI
\frac{dR}{dt} = \gamma I
dtdR=γI
Find parameters for Vancouver MSM population
Infection rate = (Rate of contact) x (Per-contact risk)
Removal rate
- Death and anti-retroviral treatment
- Sexually active
- Stable partnerships
- Number of sexual contact
- Network of contacts
- Type of exposure
- Serosorting
Study 1: TasP

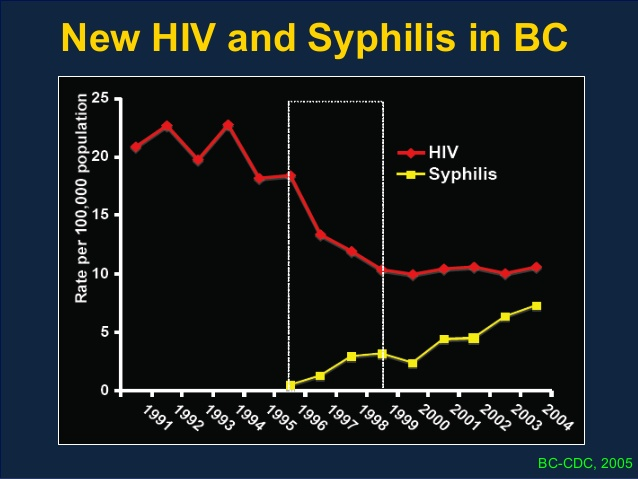
Treatment as prevention:
- Treatment for personal and population benefits
- Infectiousness correlates with viral load
- Treatment decreases VL => less infectious

Study 1: TasP
Study 1: TasP
- BC Centre for Excellence in HIV/AIDS
- Vancouver resource rich
- Free treatment by universally accessible health care
- centralized laboratory monitoring
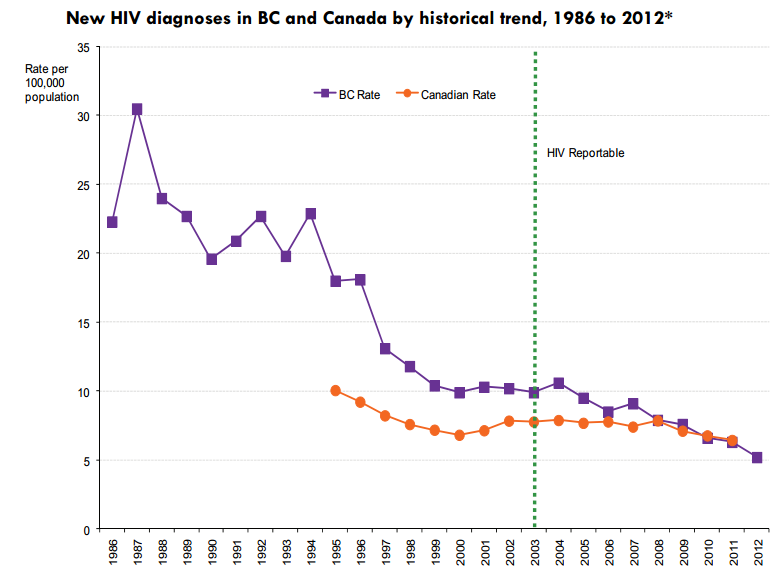
- For every 1% increase in number of individuals on suppressed HAART, HIV incidence rate decreased by 1%
- Declining trend in new HIV diagnosis in BC unique in Canada
- TasP favourable cost-benefit ratio
Study 1: TasP

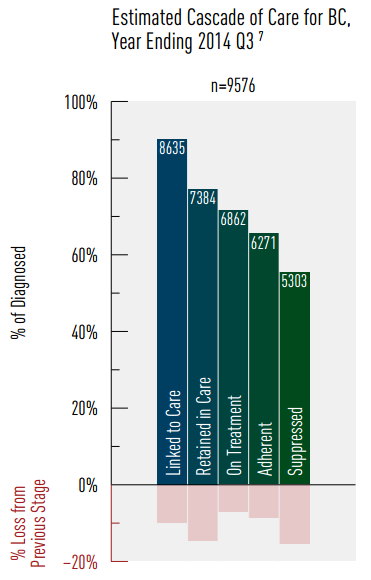
Choose parameters to fit Vancouver MSM:
- Infection rate <--> Prevalence
- Testing rate <--> HIV awareness
- Treatment rate <--> Treatment percentage
Study 2: Acute infection
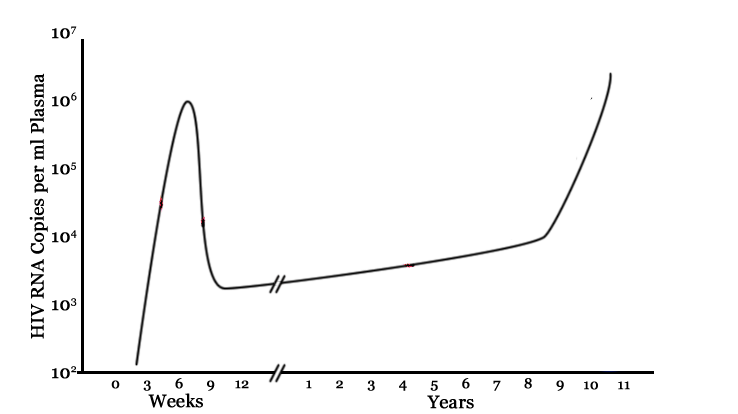
- Infectiousness correlates with viral load
- Viral load very high shortly after exposure
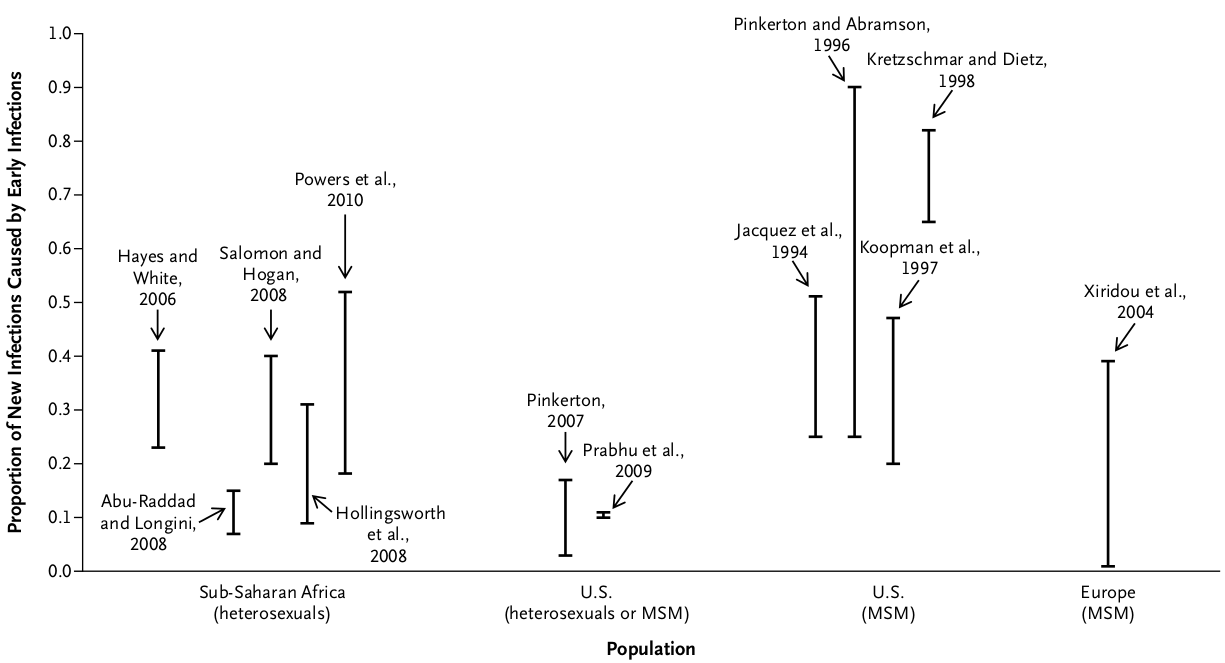
- How much of the epidemic is driven by acute infections?
Study 2: Acute infection
- Pooled NAAT tests at HIV testing clinics
- Recruitment between April 2009 and June 2012
- Very difficult to catch early infections:
- 13 participants with acute infection
- 12 with early infection
- Questionnaires on sexual activity, number of partners, use of condoms, etc.
Goal: Find acute/early infections in Vancouver
Study 2: Acute infection
Findings:
- 64% were not expecting a positive result
- Likelihood of "risky sex" decreased for first 3 months after diagnosis, remained low during follow-up, but increased over time
- All participants eventually resumed sexual activity, 92% resumed anal sex
- The 25 cases would not have been detected otherwise, hence prevented secondary cases.
Study 2: Acute infection
Study 2: Acute infection
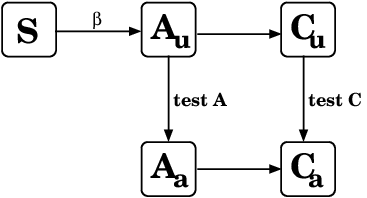
Choose parameters to fit Vancouver MSM:
- # acute infections found
Study 2: Acute infection

Choose parameters to fit Vancouver MSM:
- Effect of recent diagnosis
- Difficult to find early infections
- Are there any differences between the infected and non-infected group?
Study 3: Negative cohort
Why study HIV negative cohort?
- 166 HIV- MSM (tested at health clinic in Vancouver)
- 1 year follow-up with 4 questionnaires
- Questions similar to positive cohort
- 33 men reporting risky sex in the past 6 months, those invited to interview.
Study design
Study 3: Negative cohort
- Have you had a HIV test in the LAST 5 months?
- How many men have you had anal sex with in the LAST 3 months?
- How often do you use condoms when you are the top when having anal sex?
Example questions:
Findings: ??? - in progress
- Is the at-risk population homogeneous?
- If not,
- how much do they differ?
- how stable are the compartments?
Study 3: Negative cohort
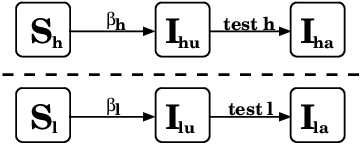
Distinguish between high-risk, low-risk
Different infection rate and testing behaviour
Study 3: Negative cohort
(How often) Do people switch between groups?
Current and Future Work
- Learn from HIV negative cohort
- Characterize, quantify risk groups
- How stable are risk groups?
- Combine study results into single model(s)
- Are ODEs the best choice?
- Exponential rates
- Relatively small populations
- Predict outcome of interventions
Thank you!
Mathematical models to quantify and optimize HIV intervention in British Columbia
By Bernhard Konrad
Mathematical models to quantify and optimize HIV intervention in British Columbia
- 513



