Going beyond collision-free motion planning...
Planning Through Contact with GCS
C. Chi et al., “Diffusion Policy: Visuomotor Policy Learning via Action Diffusion.” Mar. 09, 2023
- How do we plan for such tasks?
N. Doshi et al., “Manipulation of unknown objects via contact configuration regulation.” Jun. 01, 2022
High-level approach
- Contact modes gives a hybrid system
- Use GCS
- One vertex for each contact mode
- Simultaneously search for the mode sequence and the continuous motion
Using GCS for Planning Through Contact
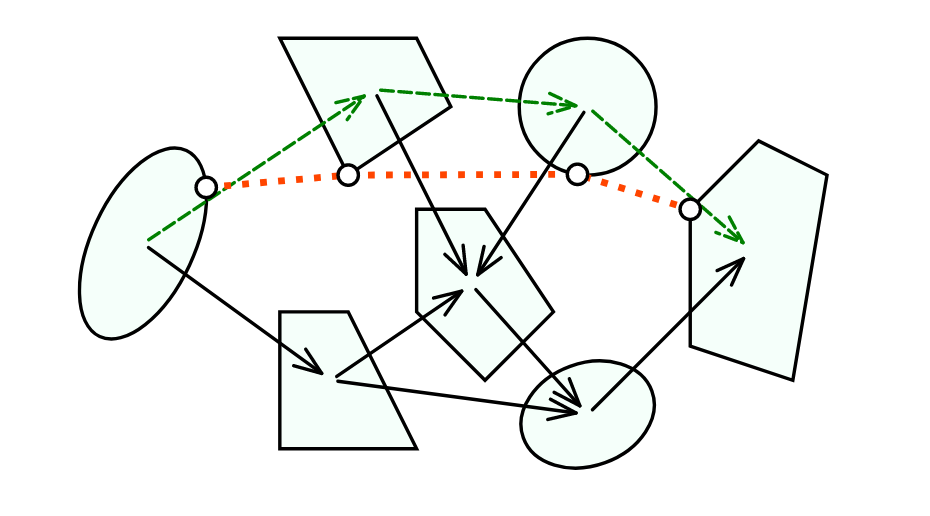
T. Marcucci, J. Umenberger, P. A. Parrilo, and R. Tedrake, “Shortest Paths in Graphs of Convex Sets.” 2022.
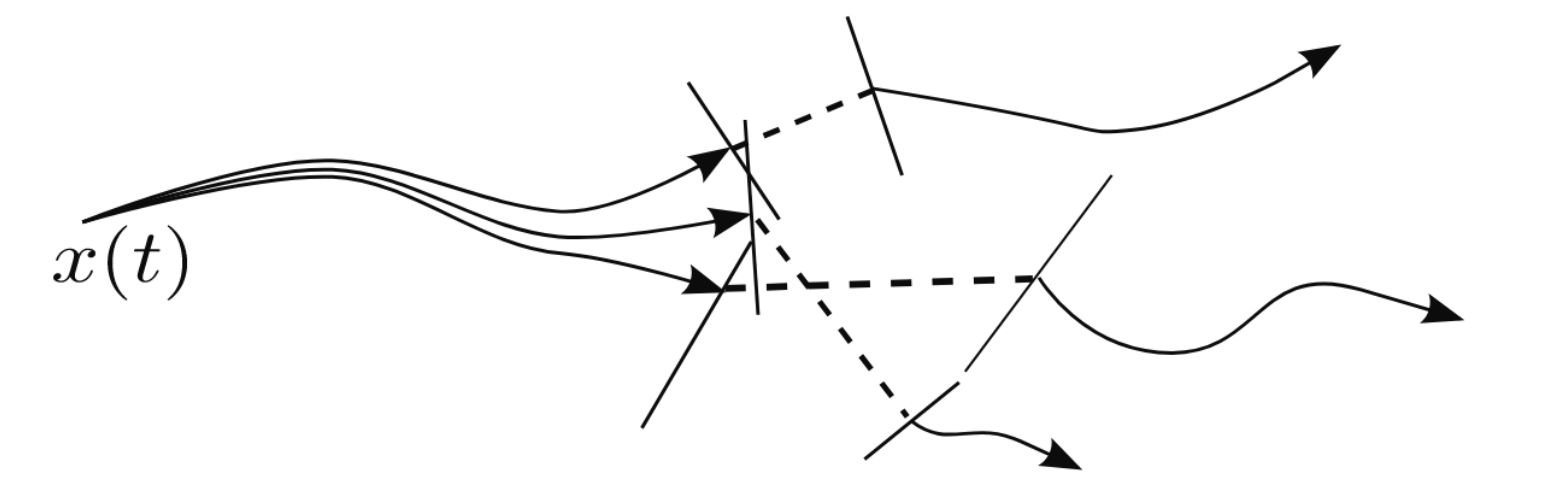
- Plan with quasi-static dynamics
- \( v \approx 0\) and \(M \dot v + C v \approx 0 \)
- No impacts
- Plan over object poses, contact forces and contact locations
Using GCS for Planning Through Contact
Formulation
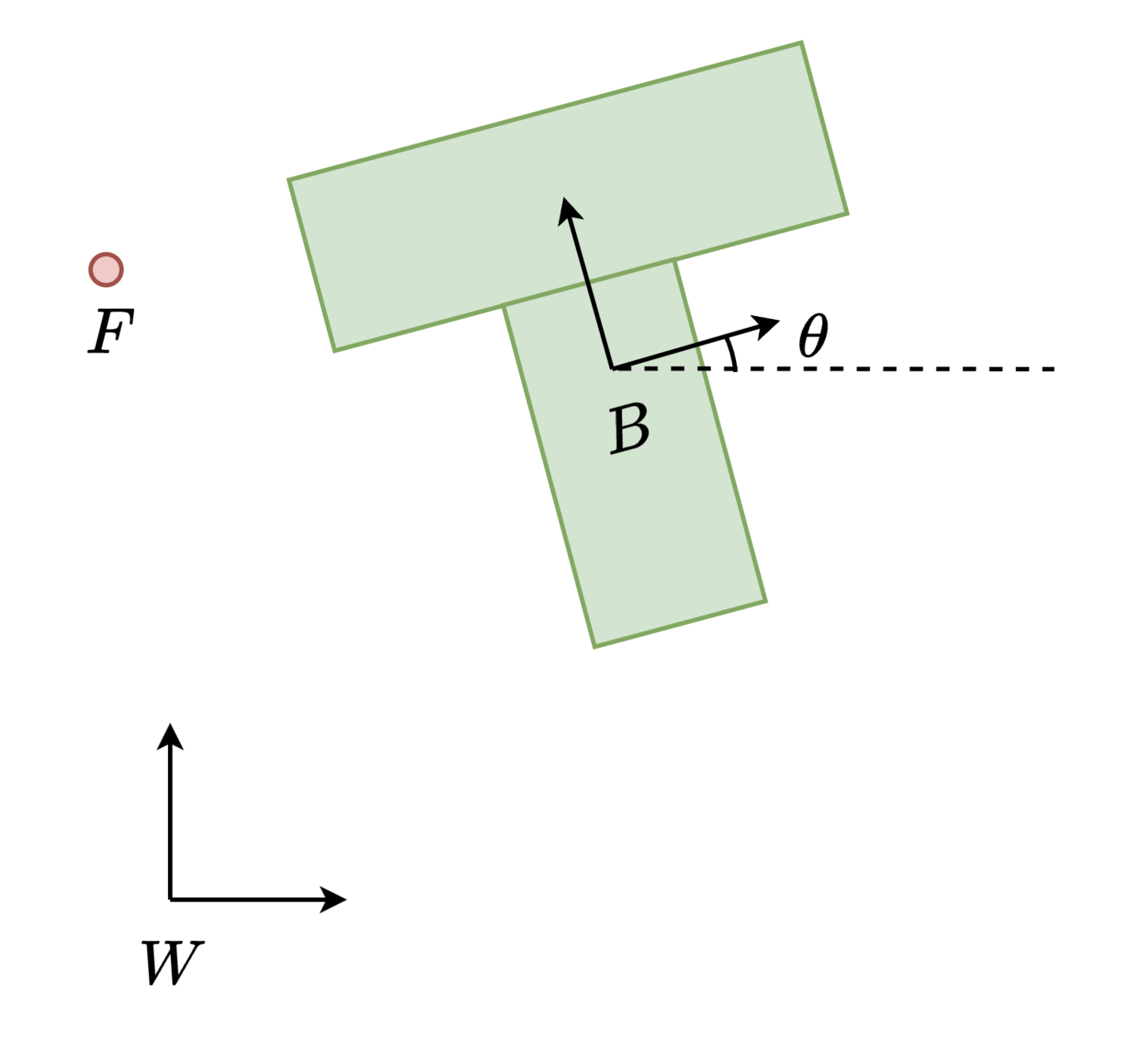
- Our quasi-static dynamics and kinematic constraints form a basic-semialgebraic set
- We can describe it as the feasible set of a QCQP
How to encode dynamics and kinematics as a convex set?
\begin{aligned}
&\tau_g(q) + \sum_i J_{c,i}^\intercal f^{c_i} = 0
\end{aligned}
{}^A R^B \in SO(2)
f^{c_i} \in \mathcal{FC}_i
\begin{aligned}
\min_{x} \quad x^\intercal Q_0 x & \\
\text{subject to}
\quad
x^\intercal Q_i x &\geq 0, \quad \forall i = 1, \ldots \\
\quad
Ax &\geq 0 \\
\quad
x &=
\begin{bmatrix}
1 \\
y
\end{bmatrix}
\end{aligned}
- A general non-convex QCQP:
- (any polynomial problem can be put in this form)
Formulate the problem as a QCQP
- (any polynomial problem can be put in this form)
Non-convex when \( Q_i \preceq 0 \)
\begin{aligned}
\min_{x} \quad x^\intercal Q_0 x & \\
\text{subject to}
\quad
x^\intercal Q_i x &\geq 0, \quad \forall i = 1, \ldots \\
\quad
Ax &\geq 0 \\
\quad
x &=
\begin{bmatrix}
1 \\
y
\end{bmatrix}
\end{aligned}
\begin{aligned}
\min_{X} \quad \langle Q_0, X \rangle & \\
\text{subject to}
\quad
\langle Q_i, X \rangle &\geq 0, \quad \forall i = 1, \ldots \\
\quad
AXA^\intercal &\geq 0 \\
\quad
AXe_1^\intercal &\geq 0 \\
\quad
e_1^\intercal X e_1 &= 1 \\
\quad
X \succeq 0 \\
\end{aligned}
\( \longrightarrow \)
- Solve for \( X \succeq 0 \) instead of for \( x \)
- Exact when \( \text{rank}(X) = 1 \iff X = x x^\intercal \)
- Feasible set is a Spectrahedron (a convex set)
\( X := xx^\intercal \)
Relaxation using Semidefinite Programming
- Build a graph of these spectrahedrons
- One for each contact mode
- Solve it using GCS!
Approach
- Exact when \( \text{rank}(X) = 1 \iff X = x x^\intercal \) \( \rightarrow\) relaxation is tight
- In general not the case (otherwise \( P = NP \) )
- Depending on the problem, relaxation can be tight
- We have a class of cost functions that often yields approximately tight solutions for our planning problem!
How good is the solution?
\(\longrightarrow\)
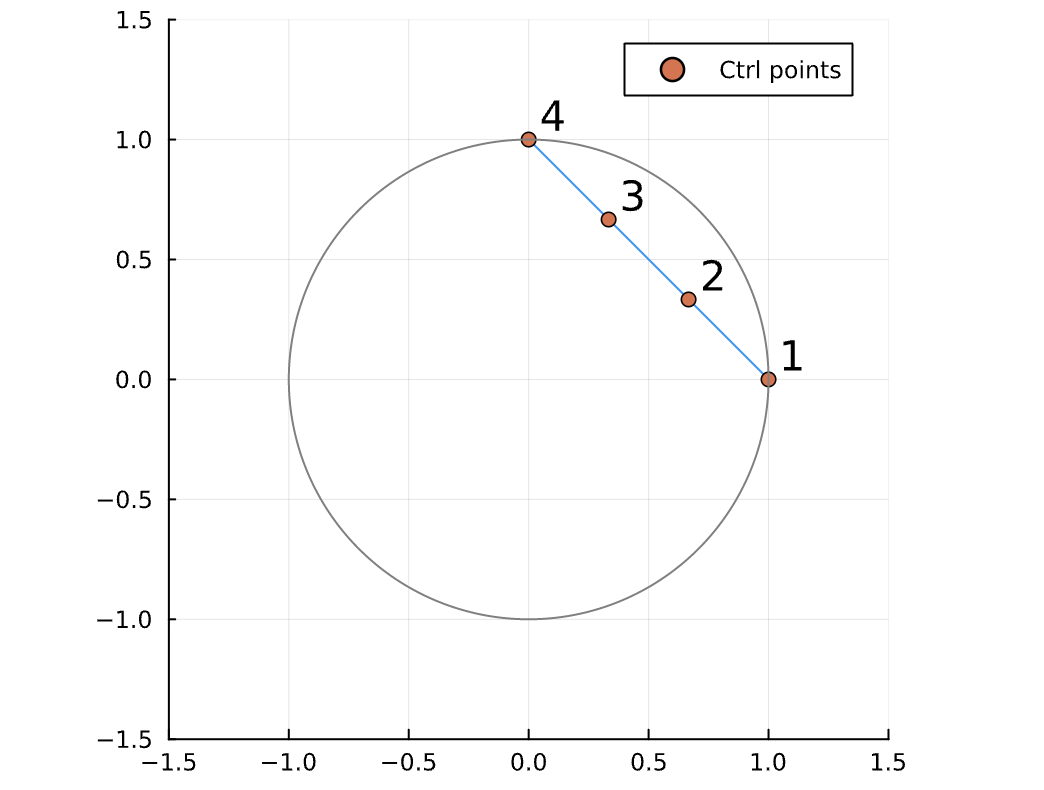
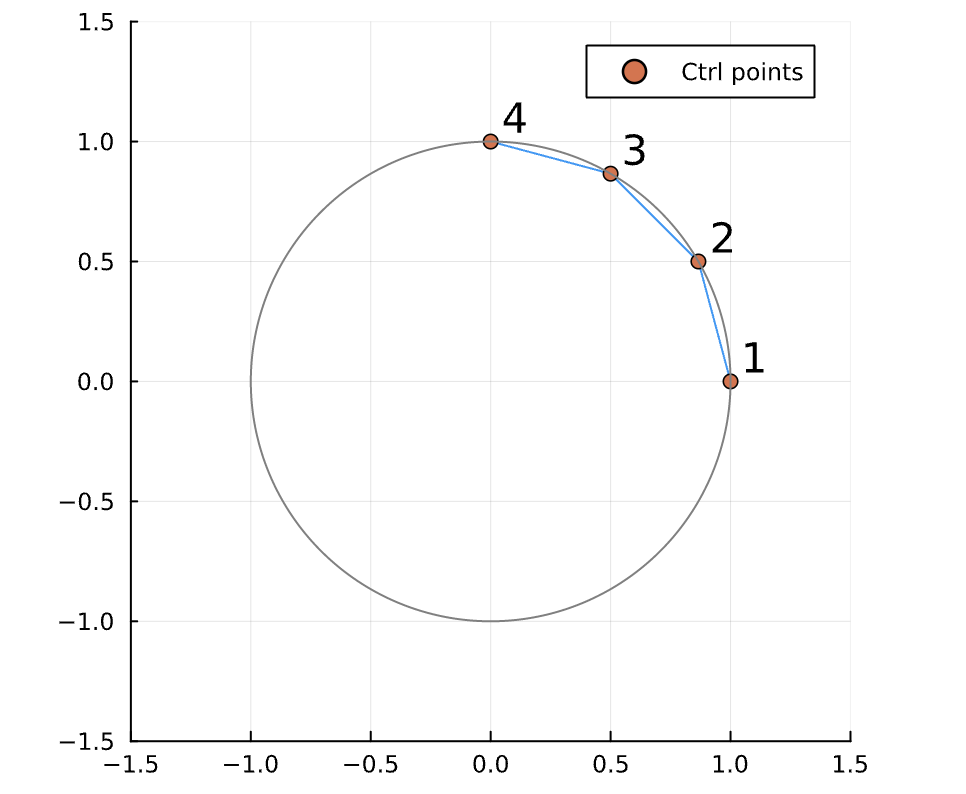
Simple example of tight solutions on SO(2)
- Hope: Convex relaxation contains enough information to take the correct high-level decisions
- Then we can refine the details as a final step!
or
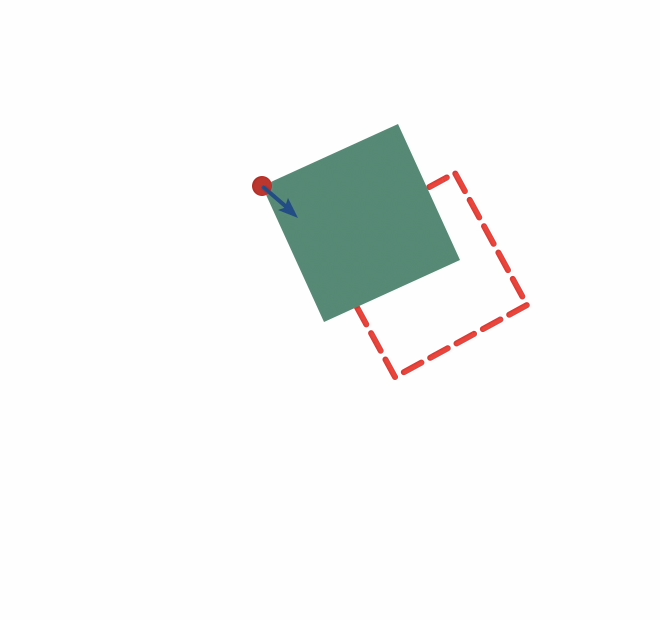
\(\longrightarrow\)
\(\longrightarrow\)
\(\longrightarrow\)
\(\longrightarrow\)
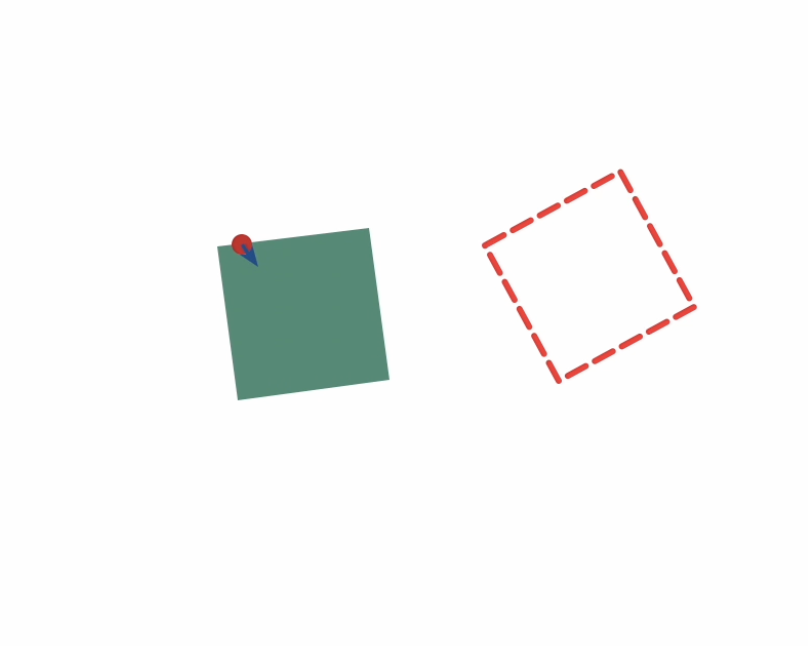
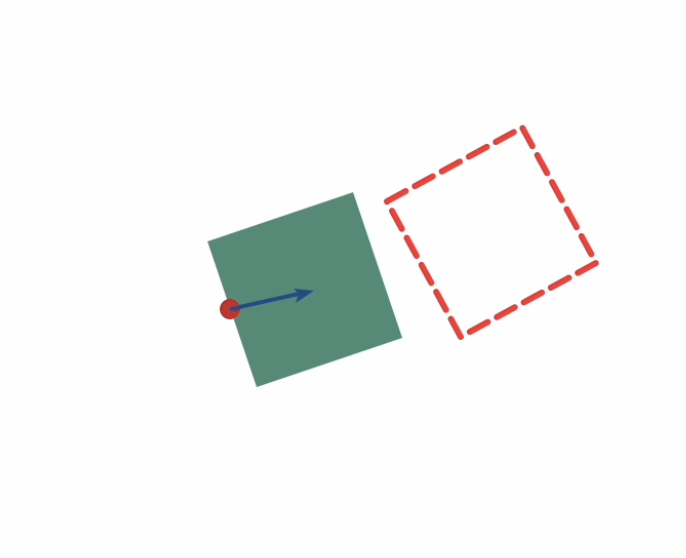
\(\longrightarrow\)
\(\longrightarrow\)
\(\longrightarrow\)
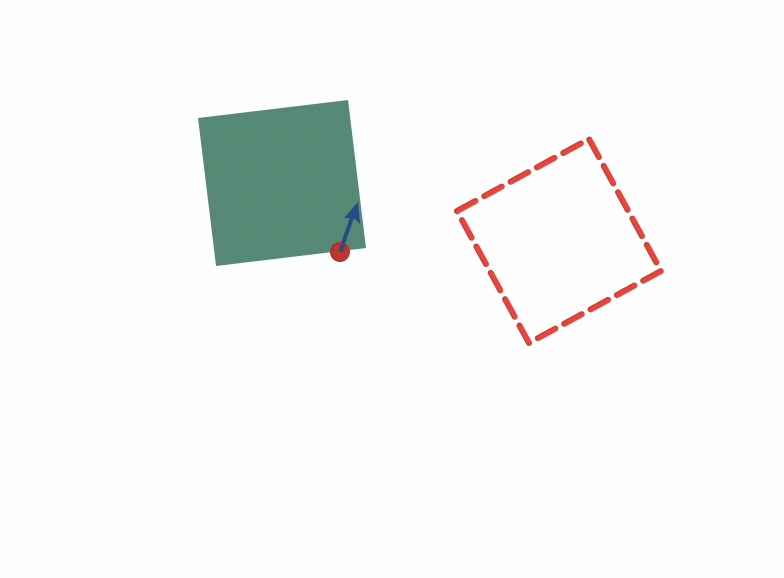
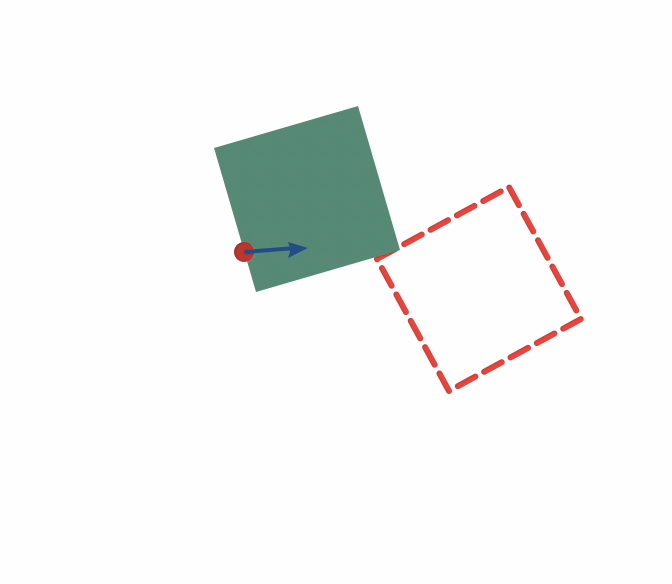
Start
Goal
Class of cost functions that give tight solutions
\begin{aligned}
K &= \int_0^T \left[ \frac{1}{2}m \lVert v (t) \rVert ^2 + \frac{1}{2} I \lVert \omega(t) \rVert^2 \right] dt
\end{aligned}
- Minimizing integrated kinetic energy of the trajectory
\(\longrightarrow\)
Obtain solutions on SO(2)!
Preliminary results on using GCS and Semidefinite relaxations for planning through contact...
Planning through contact for Planar Pushing
Planning through contact for general manipulation
Pushing on the "real" robot
- Pushing for ICRA 2023 with paper on first results
- Next step: General 3D dexterous manipulation for general rigid objects
Future work
Thank you!
Amazon Motion Planning Presentation
By Bernhard Paus Græsdal
