Long-Term Analysis of Carrier Phase Residual Variations 

Brian Breitsch

Jade Morton

Charles Rino

Using Geometry-Ionosphere-Free Combination of Triple-Frequency GPS Observations

ION GNSS 2017

Background and Motivation

Linear Estimation of GNSS Parameters

Application to Real GPS Data

Global Navigation Satellite Systems (GNSS)

...a useful everyday radio source for geophysical remote-sensing!

GPS

GLONASS

Beidou

Galileio

...etc.

GPS - Global Positioning System

  • 32-satellite constellation
  • transmit dual-frequency BPSK-moduled signals
Signal Frequency (GHz)
L1CA 1.57542
L2C 1.2276
L5 1.17645
  • new Block-IIF and next-gen

Block-III satellites transmitting triple-frequency signals

GNSS Carrier Phase Observable

\Phi_i = r + c\Delta t + T + I_i + \lambda_i N_i + H_i + S_i + \epsilon_i
Φi=r+cΔt+T+Ii+λiNi+Hi+Si+ϵi \Phi_i = r + c\Delta t + T + I_i + \lambda_i N_i + H_i + S_i + \epsilon_i

HARDWARE BIAS

IONOSPHERE RANGE ERROR

CARRIER AMBIGUITY

SYSTEMATIC ERRORS / MULTIPATH

FREQUENCY INDEPENDENT EFFECTS

STOCHASTIC ERRORS

accumulated phase (in meters) of demodulated GNSS signal at receiver for a particular satellite and signal carrier frequency \(f_i\)

Simplified Carrier Phase Model

\Phi_i = G + I_i + S_i + \epsilon_i
Φi=G+Ii+Si+ϵi\Phi_i = G + I_i + S_i + \epsilon_i

zero-mean

normally-

distributed

zero-mean

neglect bias terms

By neglecting bias terms, we address estimation precision, rather than accuracy

\Phi_i = r + c\Delta t + T + I_i + \lambda_i N_i + H_i + S_i + \epsilon_i
Φi=r+cΔt+T+Ii+λiNi+Hi+Si+ϵi \Phi_i = r + c\Delta t + T + I_i + \lambda_i N_i + H_i + S_i + \epsilon_i

"geometry" term

Ionosphere Range Error

consider first-order term in ionosphere refractive index

second and higher-order terms on the order of a few cm

I_i \approx -\frac{\kappa}{f_i^2} \displaystyle \int_\text{rx}^\text{tx} N_e \ ds = -\frac{\kappa}{f_i^2} \text{TEC}
Ii≈−κfi2∫rxtxNe ds=−κfi2TECI_i \approx -\frac{\kappa}{f_i^2} \displaystyle \int_\text{rx}^\text{tx} N_e \ ds = -\frac{\kappa}{f_i^2} \text{TEC}
\kappa = \frac{e^2}{8\pi^2\epsilon_0 m_e} \approx 40.301
κ=e28π2ϵ0me≈40.301\kappa = \frac{e^2}{8\pi^2\epsilon_0 m_e} \approx 40.301

TOTAL ELECTRON CONTENT

rx

tx

plasma / free electrons

units: \(\frac{\text{electrons}}{\text{m}^2}\)

often measured in TEC units:

1 \text{TECu} = 10^{16} \frac{\text{electrons}}{\text{m}^2}
1TECu=1016electronsm21 \text{TECu} = 10^{16} \frac{\text{electrons}}{\text{m}^2}
f_i
fif_i

carrier frequency

Estimation of \(G\) and \(\text{TEC}\) Using Dual-Frequency GNSS

neglecting systematic and stochastic error terms, and after resolving bias terms:

\text{TEC} = \displaystyle \frac{\Phi_2 - \Phi_1}{\kappa \left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right)}
TEC=Φ2−Φ1κ(1f12−1f22)\text{TEC} = \displaystyle \frac{\Phi_2 - \Phi_1}{\kappa \left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right)}
G = \displaystyle \frac{f_1^2 \Phi_1 - f_2^2 \Phi_2}{f_1^2 - f_2^2}
G=f12Φ1−f22Φ2f12−f22G = \displaystyle \frac{f_1^2 \Phi_1 - f_2^2 \Phi_2}{f_1^2 - f_2^2}

ionosphere-free combination

geometry-free combination

Examples of Dual-Frequency TEC Estimates

Poker Flat, Alaska, 2016-01-02

We compute dual-frequency TEC estimates \(\text{TEC}_\text{L1,L2}\) and \(\text{TEC}_\text{L1,L5}\)

\(G_{\text{L1,L5}} - G_{\text{L1,L2}} = \text{TEC}_{\text{L1,L5}} - \text{TEC}_{\text{L1,L2}}\)

Poker Flat, Alaska, 2016-01-02

Can we characterize / find the source of these discrepancies?

Can we relate them to errors in range and TEC estimates?

Background and Motivation

Linear Estimation of GNSS Parameters

Application to Real GPS Data

model parameters

\mathbf{\Phi} = \left[\Phi_1, \cdots, \Phi_m\right]^T
Φ=[Φ1,⋯,Φm]T\mathbf{\Phi} = \left[\Phi_1, \cdots, \Phi_m\right]^T
\mathbf{m} = \left[G, \text{TEC}, S_1, \cdots, S_m \right]^T
m=[G,TEC,S1,⋯,Sm]T\mathbf{m} = \left[G, \text{TEC}, S_1, \cdots, S_m \right]^T
\mathbf{A} = \begin{bmatrix} 1 & -\frac{\kappa}{f_1^2} & 1 & 0 & \cdots & 0 \\ 1 & -\frac{\kappa}{f_2^2} & 0 & 1 & \cdots & 0 \\ \vdots & & & & \ddots & \\ 1 & -\frac{\kappa}{f_m^2} & 0 & \cdots & & 1 \end{bmatrix}
A=[1−κf1210⋯01−κf2201⋯0⋮⋱1−κfm20⋯1]\mathbf{A} = \begin{bmatrix} 1 & -\frac{\kappa}{f_1^2} & 1 & 0 & \cdots & 0 \\ 1 & -\frac{\kappa}{f_2^2} & 0 & 1 & \cdots & 0 \\ \vdots & & & & \ddots & \\ 1 & -\frac{\kappa}{f_m^2} & 0 & \cdots & & 1 \end{bmatrix}
\mathbf{\epsilon} = [\epsilon_1, \cdots, \epsilon_m]^T
ϵ=[ϵ1,⋯,ϵm]T\mathbf{\epsilon} = [\epsilon_1, \cdots, \epsilon_m]^T
\mathbf{\Phi} = \mathbf{A} \mathbf{m} + \mathbf{\epsilon}
Φ=Am+ϵ\mathbf{\Phi} = \mathbf{A} \mathbf{m} + \mathbf{\epsilon}

Linear Inverse Problem

observations

stochastic error

forward model

Linear Estimation

\mathbf{\hat{m}} \approx \mathbf{A^*} \mathbf{\Phi}
m^≈A∗Φ\mathbf{\hat{m}} \approx \mathbf{A^*} \mathbf{\Phi}

We must apply a priori information about model parameters

\mathbf{A^*} =\begin{bmatrix} \mathbf{C}_G \\ \mathbf{C}_\text{TEC} \\ \mathbf{C}_{S_1} \\ \vdots \\ \mathbf{C}_{S_m} \end{bmatrix}
A∗=[CGCTECCS1⋮CSm]\mathbf{A^*} =\begin{bmatrix} \mathbf{C}_G \\ \mathbf{C}_\text{TEC} \\ \mathbf{C}_{S_1} \\ \vdots \\ \mathbf{C}_{S_m} \end{bmatrix}

geometry estimator

TECu estimator

systematic-error estimators

|G| , |I_i| \gg |S_i|
∣G∣,∣Ii∣≫∣Si∣|G| , |I_i| \gg |S_i|
G \sim
G∼G \sim
I \sim
I∼I \sim
S \sim
S∼S \sim

20,000 km

1 - 150 m

several cm

Linear Coefficient Constraints

Use one or two of the following constraints to reduce search space for optimal estimator coefficients:

\sum_i c_i = 0
∑ici=0\sum_i c_i = 0
\sum_i c_i = 1
∑ici=1\sum_i c_i = 1

geometry-free

geometry-estimator

\sum_i -\frac{\kappa}{f_i^2}c_i = 1
∑i−κfi2ci=1\sum_i -\frac{\kappa}{f_i^2}c_i = 1
\sum_i \frac{c_i}{f_i^2} = 0
∑icifi2=0\sum_i \frac{c_i}{f_i^2} = 0

TEC-estimator

ionosphere-free

\Phi_i = G + I_i + S_i + \epsilon_i
Φi=G+Ii+Si+ϵi\Phi_i = G + I_i + S_i + \epsilon_i

Reduction of Error

\mathbf{C}^* = \ \displaystyle \arg\min_\mathbf{C} \mathbf{C}^T \Sigma_\epsilon \mathbf{C}
C∗= argminCCTΣϵC\mathbf{C}^* = \ \displaystyle \arg\min_\mathbf{C} \mathbf{C}^T \Sigma_\epsilon \mathbf{C}

Linear combination stochastic error variance:

\sigma_\epsilon^2 = \mathbf{C}^T \mathbf{\Sigma}_\epsilon \mathbf{C}
σϵ2=CTΣϵC\sigma_\epsilon^2 = \mathbf{C}^T \mathbf{\Sigma}_\epsilon \mathbf{C}

where \(\mathbf{\Sigma}_\epsilon\) is the covariance matrix between \(\mathbf{\epsilon}_i\)

Optimal \(\mathbf{C}\) for minimizing stochastic error variance:

\(\epsilon_i\) equal-amplitude and uncorrelated

\mathbf{C}^* = \ \displaystyle \arg\min_\mathbf{C} \sum_i c_i^2
C∗= argminC∑ici2\mathbf{C}^* = \ \displaystyle \arg\min_\mathbf{C} \sum_i c_i^2

TEC Estimator

1. apply TEC-estimator constraint

2. apply geometry-free constraint (since \(|G| \gg |I_i|\) )

Dual-Frequency Example

\Rightarrow c_1 = \displaystyle -\frac{1}{\kappa \left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right)}
⇒c1=−1κ(1f12−1f22)\Rightarrow c_1 = \displaystyle -\frac{1}{\kappa \left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right)}
\begin{aligned} & -\frac{\kappa}{f_1^2}c_1 - \frac{\kappa}{f_2^2}c_2 = 1 \\[1em] & c_1 + c_2 = 0 \Rightarrow c_1 = -c_2 \\[1em] \Rightarrow & -\kappa c_1 \left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right) = 1 \end{aligned}
−κf12c1−κf22c2=1c1+c2=0⇒c1=−c2⇒−κc1(1f12−1f22)=1\begin{aligned} & -\frac{\kappa}{f_1^2}c_1 - \frac{\kappa}{f_2^2}c_2 = 1 \\[1em] & c_1 + c_2 = 0 \Rightarrow c_1 = -c_2 \\[1em] \Rightarrow & -\kappa c_1 \left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right) = 1 \end{aligned}

TEC-estimator

geometry-free

recall:

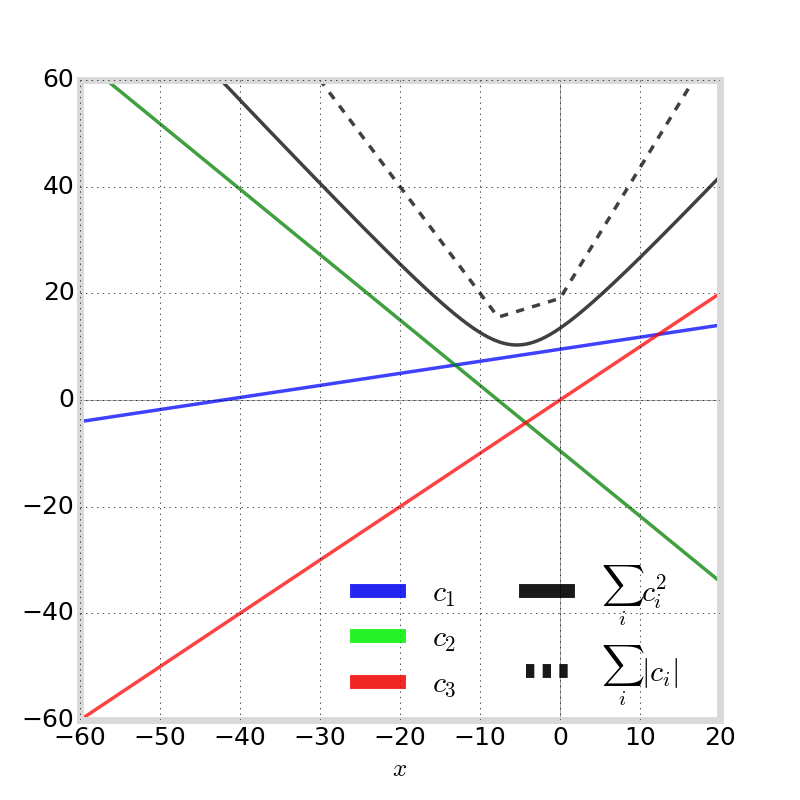
\text{TEC} = \displaystyle \frac{\Phi_2 - \Phi_1}{\kappa \left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right)}
TEC=Φ2−Φ1κ(1f12−1f22)\text{TEC} = \displaystyle \frac{\Phi_2 - \Phi_1}{\kappa \left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right)}

Triple-Frequency TEC Estimator

Applying constraints yields following system of coefficients (with free parameter denoted \(x\):

\begin{aligned} c_1 &= \frac{\frac{1}{\kappa} + x \left( \frac{1}{f_3^2} - \frac{1}{f_2^2}\right)}{\frac{1}{f_2^2} - \frac{1}{f_1^2}} \\[1em] c_2 &= \frac{-\frac{1}{\kappa} - x \left( \frac{1}{f_3^2} - \frac{1}{f_1^2}\right)}{\frac{1}{f_2^2} - \frac{1}{f_1^2}} \\[1em] c_3 & = \ \ x \end{aligned}
c1=1κ+x(1f32−1f22)1f22−1f12c2=−1κ−x(1f32−1f12)1f22−1f12c3=  x\begin{aligned} c_1 &= \frac{\frac{1}{\kappa} + x \left( \frac{1}{f_3^2} - \frac{1}{f_2^2}\right)}{\frac{1}{f_2^2} - \frac{1}{f_1^2}} \\[1em] c_2 &= \frac{-\frac{1}{\kappa} - x \left( \frac{1}{f_3^2} - \frac{1}{f_1^2}\right)}{\frac{1}{f_2^2} - \frac{1}{f_1^2}} \\[1em] c_3 & = \ \ x \end{aligned}
x^* = \frac{\frac{1}{\kappa}\left(\frac{2}{f_3^2} - \frac{1}{f_2^2} - \frac{1}{f_1^2}\right)}{\left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right)^2 + \left(\frac{1}{f_2^2} - \frac{1}{f_3^2}\right)^2 + \left(\frac{1}{f_3^2} - \frac{1}{f_1^2}\right)^2}
x∗=1κ(2f32−1f22−1f12)(1f12−1f22)2+(1f22−1f32)2+(1f32−1f12)2x^* = \frac{\frac{1}{\kappa}\left(\frac{2}{f_3^2} - \frac{1}{f_2^2} - \frac{1}{f_1^2}\right)}{\left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right)^2 + \left(\frac{1}{f_2^2} - \frac{1}{f_3^2}\right)^2 + \left(\frac{1}{f_3^2} - \frac{1}{f_1^2}\right)^2}

To satisfy \( \mathbf{C}^* = \ \displaystyle \arg\min_\mathbf{C} \sum_i c_i^2 \), choose

denote corresponding coefficient vector \(\mathbf{C}_{\text{TEC}_{1,2,3}}\) and its corresponding estimate \(\text{TEC}_{1,2,3}\)

TEC Estimator Using Triple-Frequency GPS

\begin{matrix} \text{Estimate} & c_1 & c_2 & c_3 & \sum_i c_i^2 \\[.5em] \text{TEC}_\text{L1,L2,L5} & 8.294 & -2.883 & -5.411 & 10.314 & \\ \text{TEC}_\text{L1,L5} & 7.762 & 0 & -7.762 & 10.977 & \\ \text{TEC}_\text{L1,L2} & 9.518 & -9.518 & 0 & 13.460 & \\ \text{TEC}_\text{L2,L5} & 0 & 42.080 & -42.080 & 59.510 & \end{matrix}
Estimatec1c2c3∑ici2TECL1,L2,L58.294−2.883−5.41110.314TECL1,L57.7620−7.76210.977TECL1,L29.518−9.518013.460TECL2,L5042.080−42.08059.510\begin{matrix} \text{Estimate} & c_1 & c_2 & c_3 & \sum_i c_i^2 \\[.5em] \text{TEC}_\text{L1,L2,L5} & 8.294 & -2.883 & -5.411 & 10.314 & \\ \text{TEC}_\text{L1,L5} & 7.762 & 0 & -7.762 & 10.977 & \\ \text{TEC}_\text{L1,L2} & 9.518 & -9.518 & 0 & 13.460 & \\ \text{TEC}_\text{L2,L5} & 0 & 42.080 & -42.080 & 59.510 & \end{matrix}
\mathbf{C}_{\text{TEC}_\text{L1,L2,L5}}
CTECL1,L2,L5\mathbf{C}_{\text{TEC}_\text{L1,L2,L5}}
\mathbf{C}_{\text{TEC}_\text{L1,L5}}
CTECL1,L5\mathbf{C}_{\text{TEC}_\text{L1,L5}}
\mathbf{C}_{\text{TEC}_\text{L1,L2}}
CTECL1,L2\mathbf{C}_{\text{TEC}_\text{L1,L2}}
\mathbf{C}_{\text{TEC}_\text{L2,L5}}
CTECL2,L5\mathbf{C}_{\text{TEC}_\text{L2,L5}}

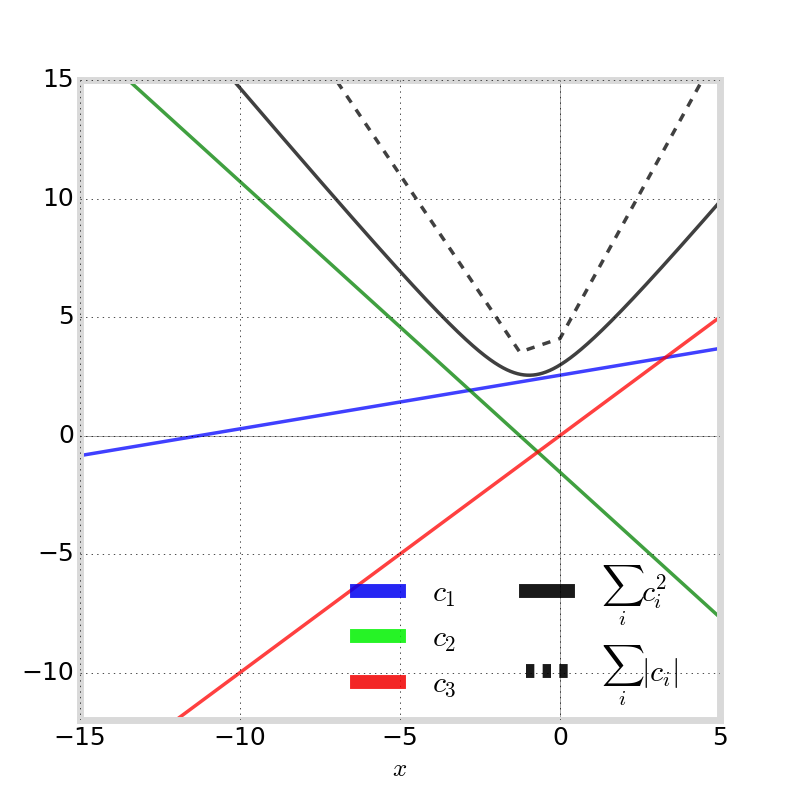
Geometry Estimator

\begin{matrix} c_1 = & \frac{-\frac{1}{f_2^2} + x \left(\frac{1}{f_2^2} - \frac{1}{f_3^2}\right)}{\frac{1}{f_1^2} - \frac{1}{f_2^2}} \\ c_2 = & \frac{\frac{1}{f_1^2} - x \left(\frac{1}{f_1^2} - \frac{1}{f_3^2}\right)}{\frac{1}{f_1^2} - \frac{1}{f_2^2}} \\ c_3 = & x \end{matrix}
c1=−1f22+x(1f22−1f32)1f12−1f22c2=1f12−x(1f12−1f32)1f12−1f22c3=x\begin{matrix} c_1 = & \frac{-\frac{1}{f_2^2} + x \left(\frac{1}{f_2^2} - \frac{1}{f_3^2}\right)}{\frac{1}{f_1^2} - \frac{1}{f_2^2}} \\ c_2 = & \frac{\frac{1}{f_1^2} - x \left(\frac{1}{f_1^2} - \frac{1}{f_3^2}\right)}{\frac{1}{f_1^2} - \frac{1}{f_2^2}} \\ c_3 = & x \end{matrix}

For triple-frequency GNSS:

1. apply geometry-estimator constraint

2. apply ionosphere-free constraint since \(I_i\) are the next-largest terms

x^* = \frac{\frac{1}{\kappa}\left(\frac{2}{f_3^2} - \frac{1}{f_2^2} - \frac{1}{f_1^2}\right)}{\left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right)^2 + \left(\frac{1}{f_2^2} - \frac{1}{f_3^2}\right)^2 + \left(\frac{1}{f_3^2} - \frac{1}{f_1^2}\right)^2}
x∗=1κ(2f32−1f22−1f12)(1f12−1f22)2+(1f22−1f32)2+(1f32−1f12)2x^* = \frac{\frac{1}{\kappa}\left(\frac{2}{f_3^2} - \frac{1}{f_2^2} - \frac{1}{f_1^2}\right)}{\left(\frac{1}{f_1^2} - \frac{1}{f_2^2}\right)^2 + \left(\frac{1}{f_2^2} - \frac{1}{f_3^2}\right)^2 + \left(\frac{1}{f_3^2} - \frac{1}{f_1^2}\right)^2}

To satisfy \( \mathbf{C}^* = \ \displaystyle \arg\min_\mathbf{C} \sum_i c_i^2 \),

We call this coefficient vector \(\mathbf{C}_{G_{1,2,3}}\) and its corresponding estimate \(G_{1,2,3}\)

the optimal "ionosphere-free combination"

Geometry Estimator Using Triple-Frequency GPS

\begin{matrix} \text{Estimate} & c_1 & c_2 & c_3 & \sum_i c_i^2 \\[.5em] G_\text{L1,L2,L5} & 2.327 & -0.360 & -0.967 & 2.546 \\ G_\text{L1,L5} & 2.261 & 0 & -1.261 & 2.588 \\ G_\text{L1,L2} & 2.546 & -1.546 & 0 & 2.978 \\ G_\text{L2,L5} & 0 & 12.255 & -11.255 & 16.639 \end{matrix}
Estimatec1c2c3∑ici2GL1,L2,L52.327−0.360−0.9672.546GL1,L52.2610−1.2612.588GL1,L22.546−1.54602.978GL2,L5012.255−11.25516.639\begin{matrix} \text{Estimate} & c_1 & c_2 & c_3 & \sum_i c_i^2 \\[.5em] G_\text{L1,L2,L5} & 2.327 & -0.360 & -0.967 & 2.546 \\ G_\text{L1,L5} & 2.261 & 0 & -1.261 & 2.588 \\ G_\text{L1,L2} & 2.546 & -1.546 & 0 & 2.978 \\ G_\text{L2,L5} & 0 & 12.255 & -11.255 & 16.639 \end{matrix}
\mathbf{C}_{G_\text{L1,L2,L5}}
CGL1,L2,L5\mathbf{C}_{G_\text{L1,L2,L5}}
\mathbf{C}_{G_\text{L1,L5}}
CGL1,L5\mathbf{C}_{G_\text{L1,L5}}
\mathbf{C}_{G_\text{L1,L2}}
CGL1,L2\mathbf{C}_{G_\text{L1,L2}}
\mathbf{C}_{G_\text{L2,L5}}
CGL2,L5\mathbf{C}_{G_\text{L2,L5}}

Systematic Error Estimator

Since \(|G| \gg |I_i| \gg |S_i|\), must apply both geometry-free and ionosphere-free constraints

For triple-frequency GNSS:

\begin{aligned} c_1 & = \ \ x \frac{\frac{1}{f_3^2} - \frac{1}{f_2^2}}{\frac{1}{f_2^2} - \frac{1}{f_1^2}} \\[1em] c_2 & = - x \frac{\frac{1}{f_3^2} - \frac{1}{f_1^2}}{\frac{1}{f_2^2} - \frac{1}{f_1^2}} \\[1em] c_3 & = \ \ x \end{aligned}
c1=  x1f32−1f221f22−1f12c2=−x1f32−1f121f22−1f12c3=  x\begin{aligned} c_1 & = \ \ x \frac{\frac{1}{f_3^2} - \frac{1}{f_2^2}}{\frac{1}{f_2^2} - \frac{1}{f_1^2}} \\[1em] c_2 & = - x \frac{\frac{1}{f_3^2} - \frac{1}{f_1^2}}{\frac{1}{f_2^2} - \frac{1}{f_1^2}} \\[1em] c_3 & = \ \ x \end{aligned}

system is linear subspace

there is "only one" estimate of systematic errors

note this requires \(m \ge 3\)

Geometry-Ionosphere-Free Combination

FACT: The difference between any two geometry term or any two TEC estimates produces some scaling of the GIFC

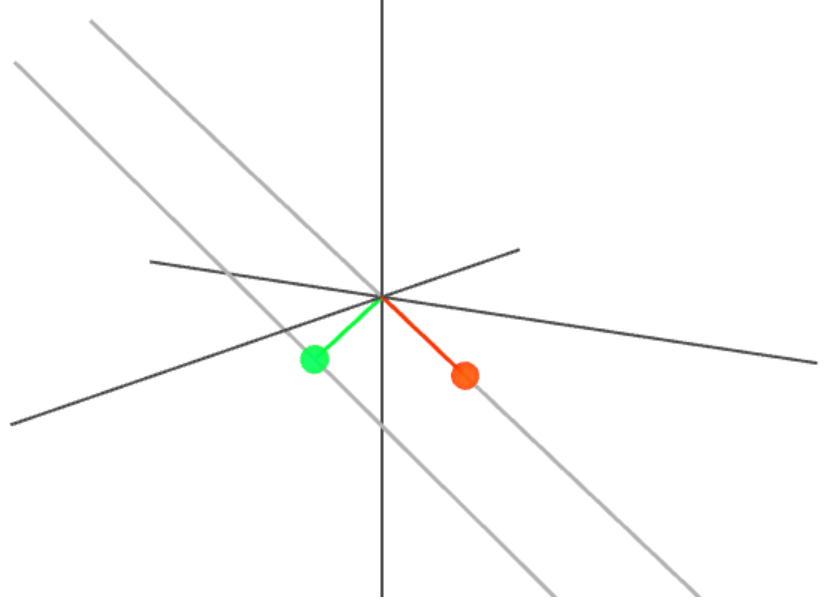
FACT: \(\mathbf{C}_\text{GIFC} \perp \mathbf{C}_{G_{1,2,3}}\) and \(\mathbf{C}_\text{GIFC} \perp \mathbf{C}_{\text{TEC}_{1,2,3}}\)

\mathbf{C}_{\text{TEC}_{1,2,3}}
CTEC1,2,3\mathbf{C}_{\text{TEC}_{1,2,3}}
\mathbf{C}_\text{GIFC}
CGIFC\mathbf{C}_\text{GIFC}

information about systematic and stochastic errors present in GNSS carrier phase observables

GIFC Triple-Frequency GPS

\begin{aligned} \mathbf{C}_{\text{GIFC}_\text{L1,L2,L5}} & = \mathbf{C}_{\text{TEC}_{\text{L1,L5}}} - \mathbf{C}_{\text{TEC}_{\text{L1,L2}}} \\[1em] & = \left[-1.756, 9.520, -7.764\right]^T \end{aligned}
CGIFCL1,L2,L5=CTECL1,L5−CTECL1,L2=[−1.756,9.520,−7.764]T\begin{aligned} \mathbf{C}_{\text{GIFC}_\text{L1,L2,L5}} & = \mathbf{C}_{\text{TEC}_{\text{L1,L5}}} - \mathbf{C}_{\text{TEC}_{\text{L1,L2}}} \\[1em] & = \left[-1.756, 9.520, -7.764\right]^T \end{aligned}

We (arbitrarily) choose:

Note: the triple-frequency GIFC does not have a well-defined unit.

GIFC in our results section have the scaling shown here.

Background and Motivation

Linear Estimation of GNSS Parameters

Application to Real GPS Data

Experiment Data

GPS Lab high-rate GNSS data collection network

  • Alaska, Hong Kong, Peru
  • 2013, 2014, 2015, 2016
  • 1 Hz GPS L1/L2/L5 measurements
  • Septentrio PolarXs

GIFC Examples

Peru G24

Hong Kong G24

Peru G25

Alaska G01

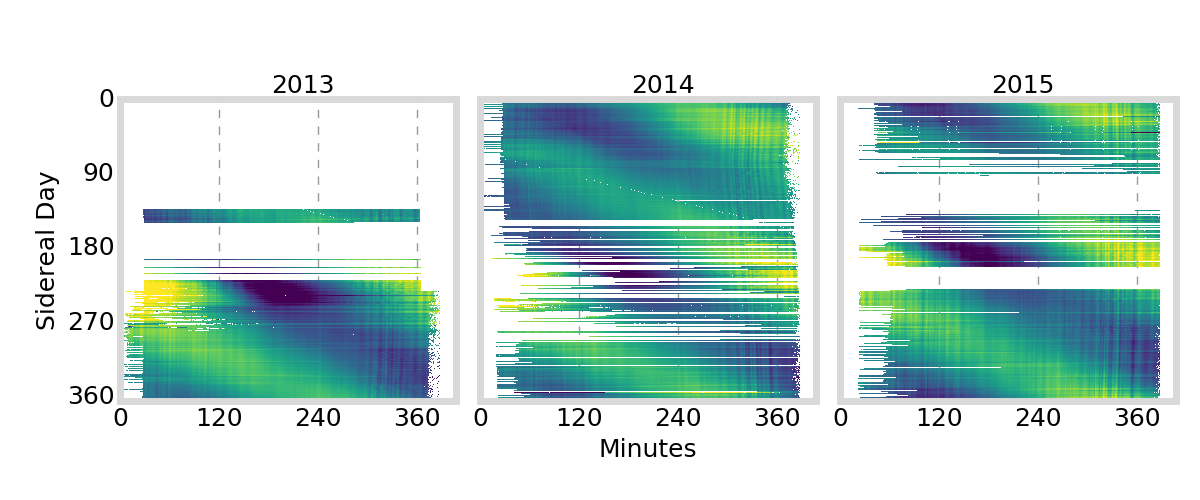
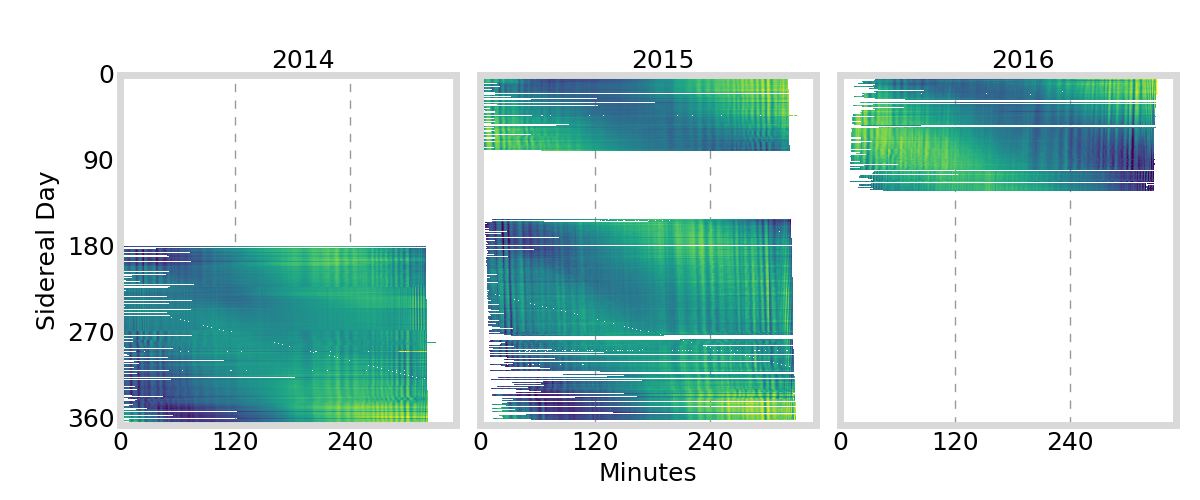
GIFC Calendar

Hong Kong G24

Alaska G25

Alaska G01

  • large, long-term GIFC trend likely due mostly to satellite thermal oscillations
  • studied by (Montebruck et. al. 2012) and (Li et. al. 2013)

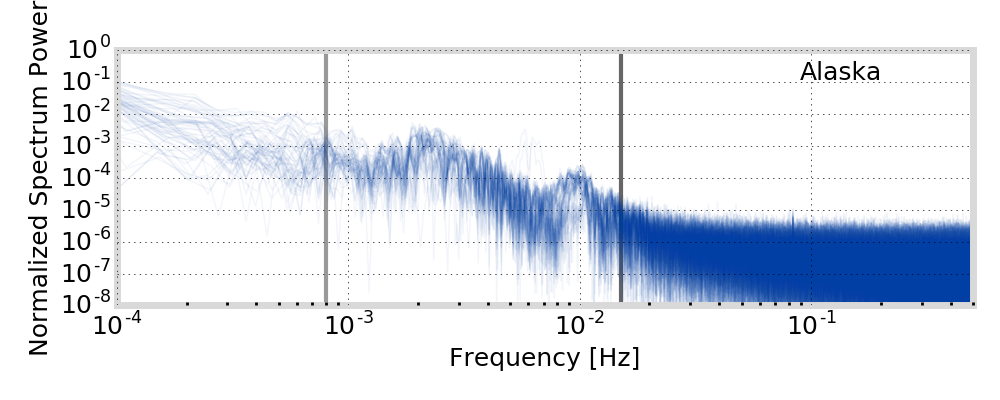
GIFC Spectrum

Alaska

Hong Kong

Peru

GIFC Histogram

Peru Example

Conclusions

  • GIFC is an indicator of the presence of systematic / stochastic errors
  • two main components to GIFC
    • large, low-frequency trend (likely due to satellite thermal oscillations)
    • multipath
  • this work is a step towards improved assessment of precision of GNSS phase-related estimates, particularly ionosphere TEC
  • small improvement of triple-frequency estimators over dual-frequency signal pair with widest frequency separation

References

O. Montenbruck, U. Hugentobler, R. Dach, P. Steigenberger, and A. Hauschild, “Apparent clock variations of the Block IIF-1 (SVN62) GPS satellite,” GPS Solutions, vol. 16, no. 3, pp. 303–313, 2012.

 

H. Li, X. Zhou, and B. Wu, “Fast estimation and analysis of the inter-frequency clock bias for Block IIF satellites,” GPS Solutions, vol. 17, no. 3, pp. 347–355, 2013.

Acknowledgements

This research was supported by the Air Force Research Laboratory and NASA.

ION GNSS 2017 - Information From Multi-Frequency GNSS

By Brian Breitsch

ION GNSS 2017 - Information From Multi-Frequency GNSS

  • 666

More from Brian Breitsch