Lecture on Fuzzy Dark Matter Cosmology
Bodo Schwabe
Overview
- Cold dark matter explains cosmological observations
- But potential short comings on galactic scales
- Fuzzy dark matter theory
- Fuzzy dark matter observables
Successes of cold dark matter
( + cosmological constant )
Centripetal force = Gravitational force
rv2(r)=r2Gm(r)
\frac{v^2(r)}{r} = \frac{Gm(r)}{r^2}
v(r)=rGm(r)
v(r) = \sqrt{\frac{Gm(r)}{r}}
See also arXiv:1905.08103 for a jupyter notebook to reproduce this data
Potential shortcomings on "small" galactic scales
Title Text
The ΛCDM model encounters problems in describing structures at small scales. The main problems are/have been
-
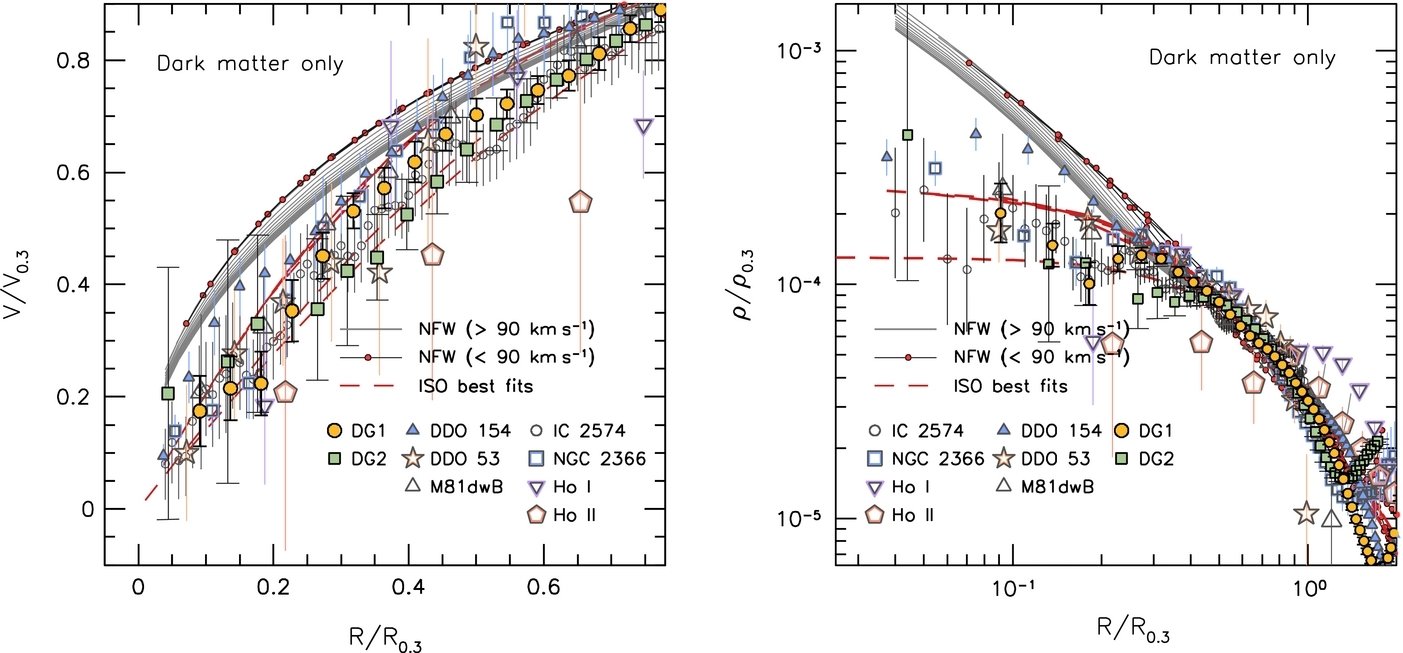
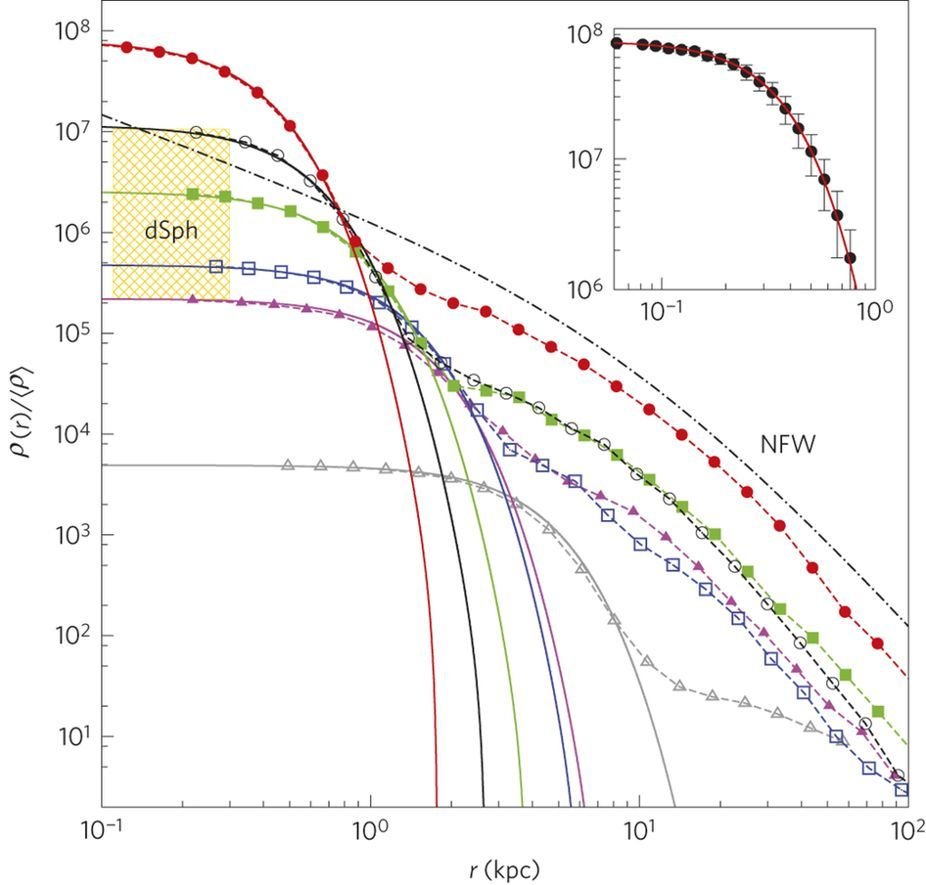
The "cusp/core problem", designating the discrepancy between the flat density profiles of dwarf galaxies, Irregulars, and Low Surface Brightness galaxies, and the cuspy profile predicted by dissipationless N-body simulations, despite the fact that the observed galaxies are all of DM dominated types.
[arXiv:1606.07790 ]
[arXiv: 1011.2777]
Title Text
The ΛCDM model encounters problems in describing structures at small scales. The main problems are/have been
-
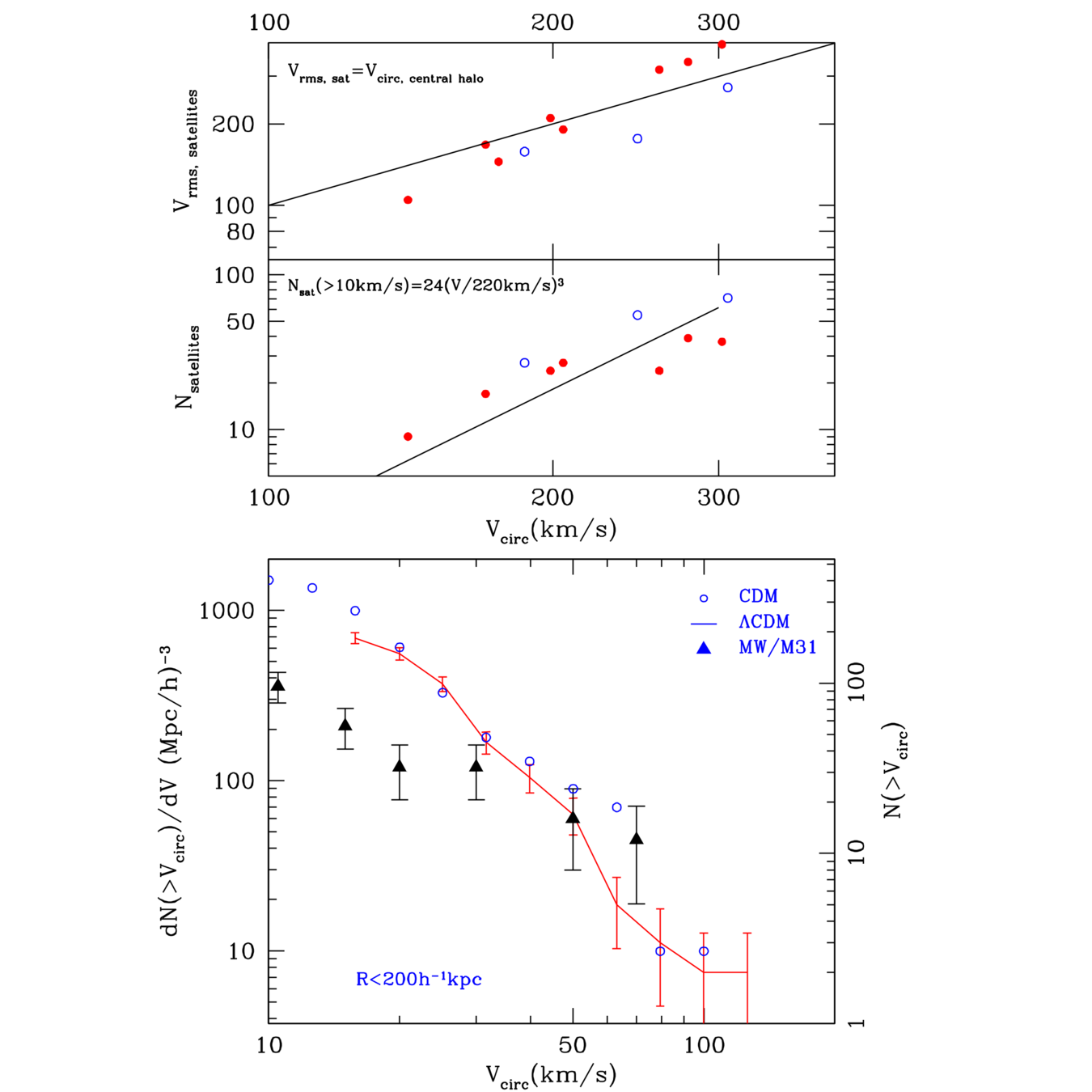
The “missing satellite problem”, coining the discrepancy between the number of predicted subhalos in N-body simulations and those actually observed.
[arXiv:1606.07790 ]
Title Text
The ΛCDM model encounters problems in describing structures at small scales. The main problems are/have been
-
,“Too Big To Fail” problem, arising from the ΛCDM prediction of satellites that are too massive and too dense, compared to those observed, to hope for their destruction in the history of mass assembly up to today.
[arXiv:1606.07790 ]
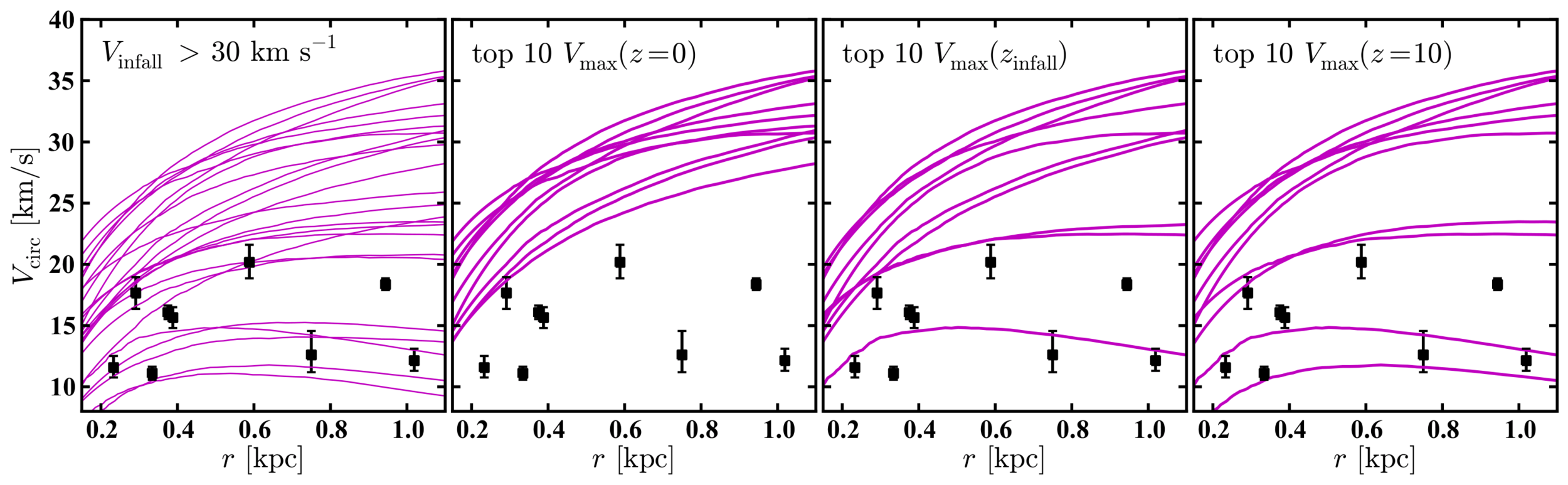
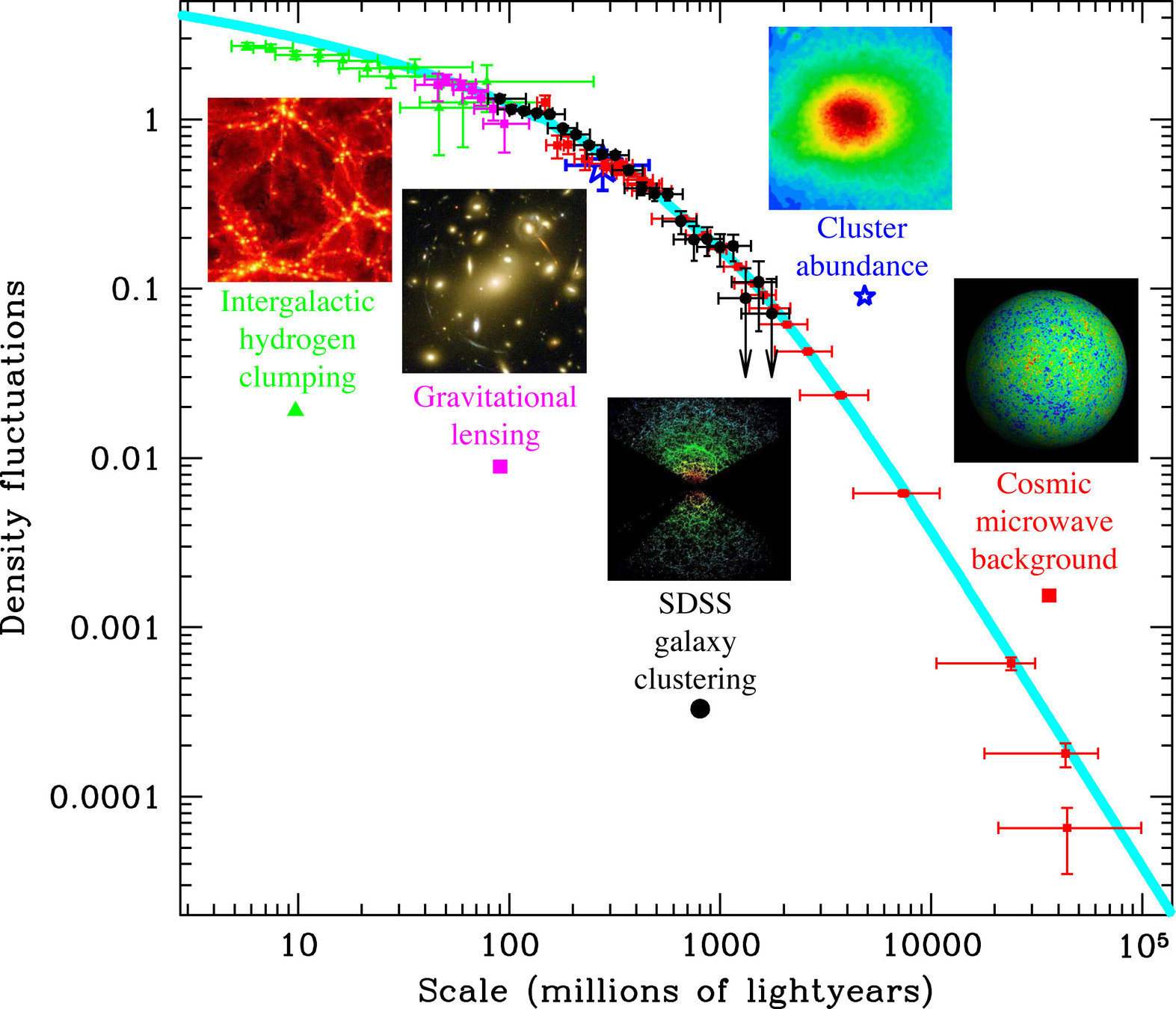
All of these problems have in common that N-body simulations modelling cold dark matter predict more substructure on galactic scales
[arXiv:1301.4498]
Fuzzy dark matter theory
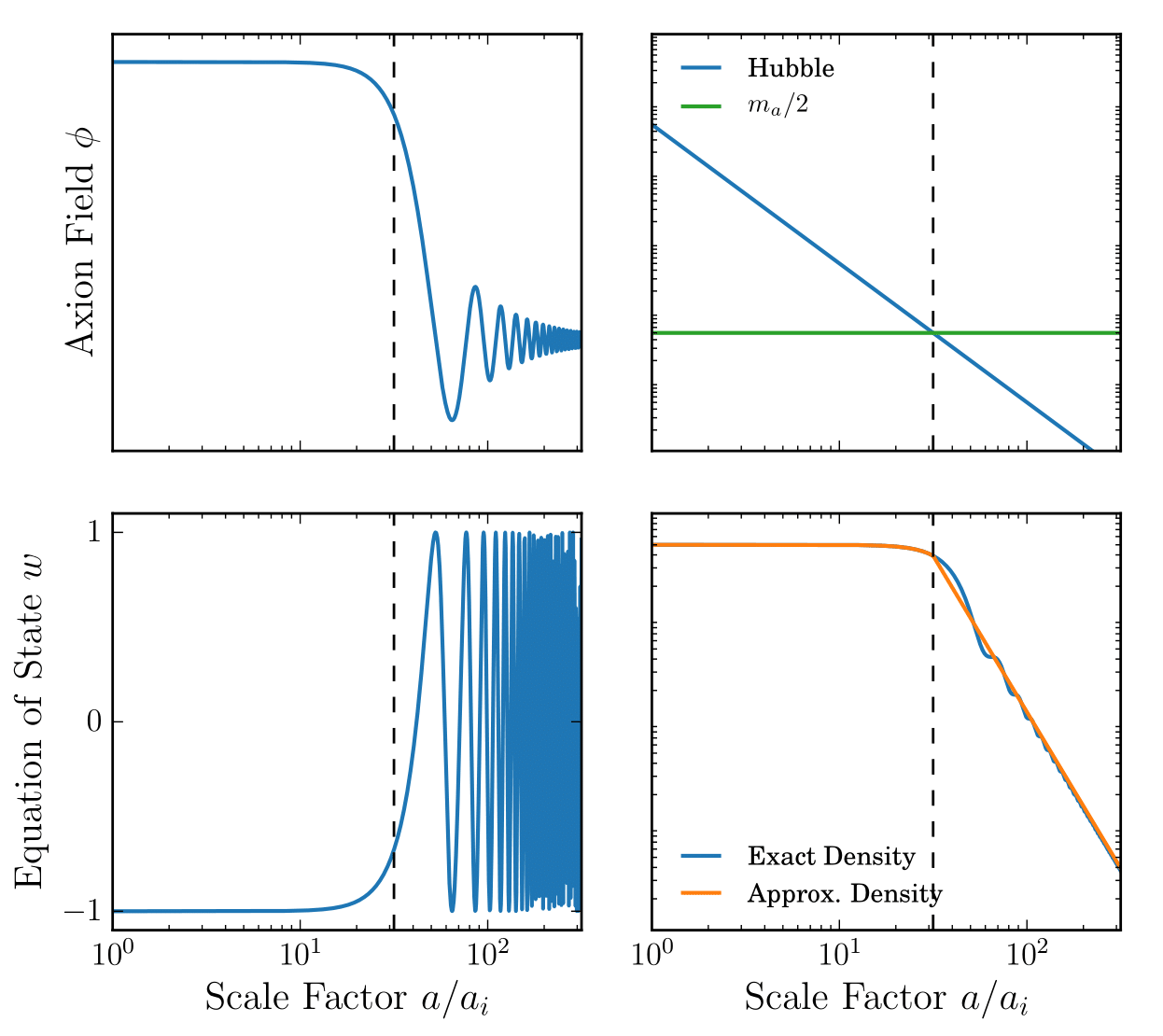
The Cosmological Axion/FDM Field
ϕ¨+3Hϕ˙−∇2ϕ+ma2ϕ=0
\ddot{\phi}+3H\dot{\phi}-\nabla^2\phi+m_a^2\phi=0
Axion equation of motion:
Background energy density and pressure:
ρa=21ϕ˙2+21ma2ϕ2Pa=21ϕ˙2−21ma2ϕ2Pa=ωaρa
\overline{\rho}_a=\frac{1}{2}\dot{\phi}^2+\frac{1}{2}m_a^2\phi^2 \\
\overline{P}_a=\frac{1}{2}\dot{\phi}^2-\frac{1}{2}m_a^2\phi^2 \\
\overline{P}_a=\omega_a\overline{\rho}_a
ϕ=a−3/2(t/ti)1/2[C1Jn(mat)+C2Yn(mat)]
\phi=a^{-3/2}(t/t_i)^{1/2}[C_1J_n(m_at)+C_2Y_n(m_at)]
Solution:
[arXiv:1510.07633]
The non-relatistic limit
[arXiv:2104.10128]
ϕ=2mℏψe−imt/ℏ
\phi = \frac{\hbar}{\sqrt{2}m}\overline{\psi} e^{-imt/\hbar}
iℏ∂tψ=−2a2mℏ2∇2ψ+mVψ
i\hbar\partial_{t}\psi = -\frac{\hbar^{2}}{2a^{2}m}\nabla^{2}\psi+mV\psi
(gμν∇μ∇ν−ℏ2m2)ϕ=0
\left(g^{\mu\nu}\nabla_{\mu}\nabla_{\nu}-\frac{m^{2}}{\hbar^{2}}\right)\phi = 0
Tμν=∇μϕ∇νϕ−21gμν(gρσ∇ρϕ∇σϕ+ℏ2m2ϕ)
T_{\mu\nu} = \nabla_{\mu}\phi\nabla_{\nu}\phi-\frac{1}{2}g_{\mu\nu}\left(g^{\rho\sigma}\nabla_{\rho}\phi\nabla_{\sigma}\phi+\frac{m^{2}}{\hbar^{2}}\phi\right)
Rμν−21gμνR=8πGTμν
R_{\mu\nu}-\frac{1}{2}g_{\mu\nu}R = 8\pi GT_{\mu\nu}
∇2V=4πGa−1δρ
\nabla^{2}V = 4\pi Ga^{-1}\delta\rho
δρ=∣ψ∣2
\delta\rho=|\psi|^{2}
Madelung Transformation - Bohmian Quantum Mechanics
iℏ∂tψ=−2a2mℏ2∇2ψ+mVψ
i\hbar\partial_{t}\psi = -\frac{\hbar^{2}}{2a^{2}m}\nabla^{2}\psi+mV\psi
ψ=ρeiS/ℏ
\psi = \sqrt{\rho}e^{iS/\hbar}
∂tρ=−2ma21[2(∇ρ)⋅(∇S)+ρ∇2S]
\partial_{t}\sqrt{\rho} = -\frac{1}{2ma^{2}}\left[2(\nabla\sqrt{\rho})\cdot(\nabla S)+\sqrt{\rho}\nabla^{2}S\right]
imaginary part
v=∇mS
\textbf{v}=\nabla\frac{S}{m}
∂tρ+a21∇⋅(ρv)=0
\partial_{t}\rho+\frac{1}{a^{2}}\nabla\cdot(\rho\textbf{v}) = 0
real part
∂tS=−[2a2m(∇S)2+mV+Q]
\partial_{t} S = -\left[\frac{(\nabla S)^{2}}{2a^{2}m}+mV+Q\right]
Q=−2ma2ℏ2ρ∇2ρ
Q = -\frac{\hbar^{2}}{2ma^{2}}\frac{\nabla^{2}\sqrt{\rho}}{\sqrt{\rho}}
∂tv+a21v⋅∇v+∇V+∇Q=0
\partial_{t}\textbf{v}+\frac{1}{a^{2}}\textbf{v}\cdot\nabla\textbf{v}+\nabla V+\nabla Q = 0
Euler equations of fluid dynamics + quantum corrections !
Schroedinger-Vlasov correspondence similarly to Ehrenfest theorem tells you that FDM behaves like CDM on large scales where gradient energy averages out !
[arXiv:1403.5567]
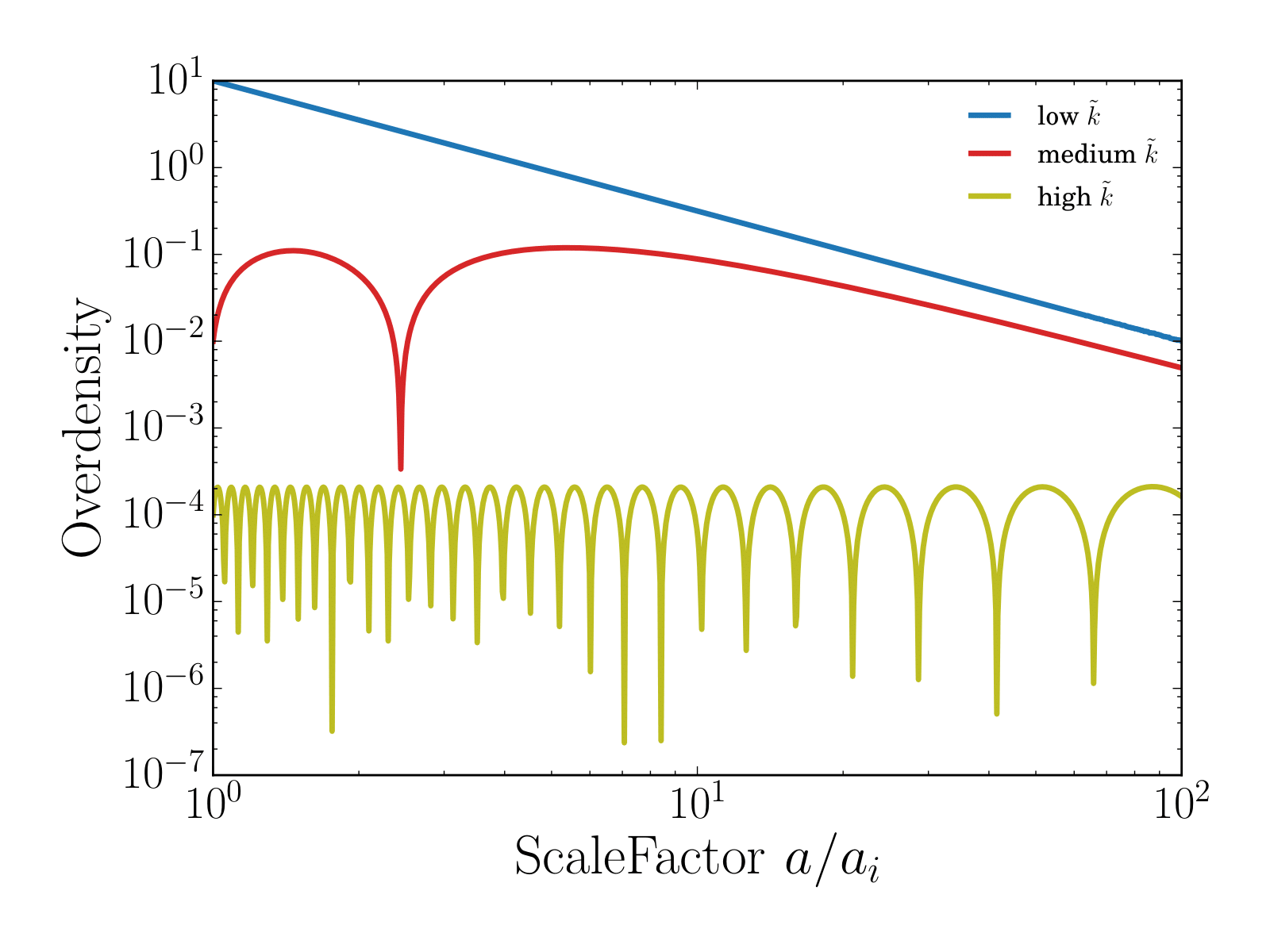
Linear growth of perturbations
a2∂tδρ+ρ0∇⋅v=0
a^{2}\partial_{t}\delta\rho+\rho_{0}\nabla\cdot\textbf{v} = 0
ρ0∂tv+ρ0∇V−4m2a2ℏ2∇(∇2δρ)=0
\rho_{0}\partial_{t}\textbf{v}+\rho_{0}\nabla V-\frac{\hbar^{2}}{4m^{2}a^{2}}\nabla\left(\nabla^{2}\delta \rho\right) = 0
Linearize Euler equations:
Take time derivative of the first equation and spatial derivative of the second one, combine and take Fourier transform
∂t2ρk+2H∂tρk+(4m2a4ℏ2k4−4πGρ0)ρk=0
\partial_{t}^2\rho_{k}+2H\partial_{t}\rho_{k}+\left(\frac{\hbar^{2}k^{4}}{4m^{2}a^{4}}-4\pi G \rho_0\right)\rho_{k} = 0
Last term vanishes at Jeans scale
kJ=(16πGaρ0)1/4m1/2
k_J=(16 \pi Ga \rho_{0})^{1/4}m^{1/2}
Jeans scale vs. deBroglie wavelength
λdB=2πℏ(mv)−1
\lambda_{\rm dB}=2\pi\hbar(mv)^{-1}
≃ℏm−1(Gρ)−1/2r−1
\simeq\hbar m^{-1}(G\rho)^{-1/2}r^{-1}
v≃r/tff=rGρ
v\simeq r/t_{\text{ff}} = r\sqrt{G\rho}
λdB≡r
\lambda_{\rm dB}\equiv r
λdB≃rJ
\lambda_{\rm dB}\simeq r_J
≃66.5a1/4(0.12Ωah2)1/4(10−22 eVm)1/2 Mpc−1
\simeq 66.5 a^{1/4}\left(\frac{\Omega_a h^2}{0.12}\right)^{1/4}\left( \frac{m}{10^{-22}\text{ eV}}\right)^{1/2}\text{ Mpc}^{-1}
Linear growth of perturbations
∂t2ρk+2H∂tρk+(4m2a4ℏ2k4−4πGρ0)ρk=0
\partial_{t}^2\rho_{k}+2H\partial_{t}\rho_{k}+\left(\frac{\hbar^{2}k^{4}}{4m^{2}a^{4}}-4\pi G \rho_0\right)\rho_{k} = 0
δa=C1D+(k,a)+C2D−(k,a)
\delta_a=C_1 D_+(k,a)+C_2D_-(k,a)
D+(k,a)=k~23asin(ak~2)+[k~43a−1]cos(ak~2)
D_+(k,a)= \frac{3\sqrt{a}}{\tilde{k}^2}\sin \left( \frac{\tilde{k}^2}{\sqrt{a}} \right) +\left[ \frac{3a}{\tilde{k}^4}-1 \right]\cos \left( \frac{\tilde{k}^2}{\sqrt{a}} \right)
D−(k,a)=[k~43a−1]sin(ak~2)−k~23acos(ak~2)
D_-(k,a)= \left[ \frac{3a}{\tilde{k}^4}-1\right] \sin \left( \frac{\tilde{k}^2}{\sqrt{a}} \right) -\frac{3\sqrt{a}}{\tilde{k}^2}\cos \left( \frac{\tilde{k}^2}{\sqrt{a}} \right)
k~=k/maH0∝k/kJ
\tilde{k}=k/\sqrt{m_aH_0}\propto k/k_J
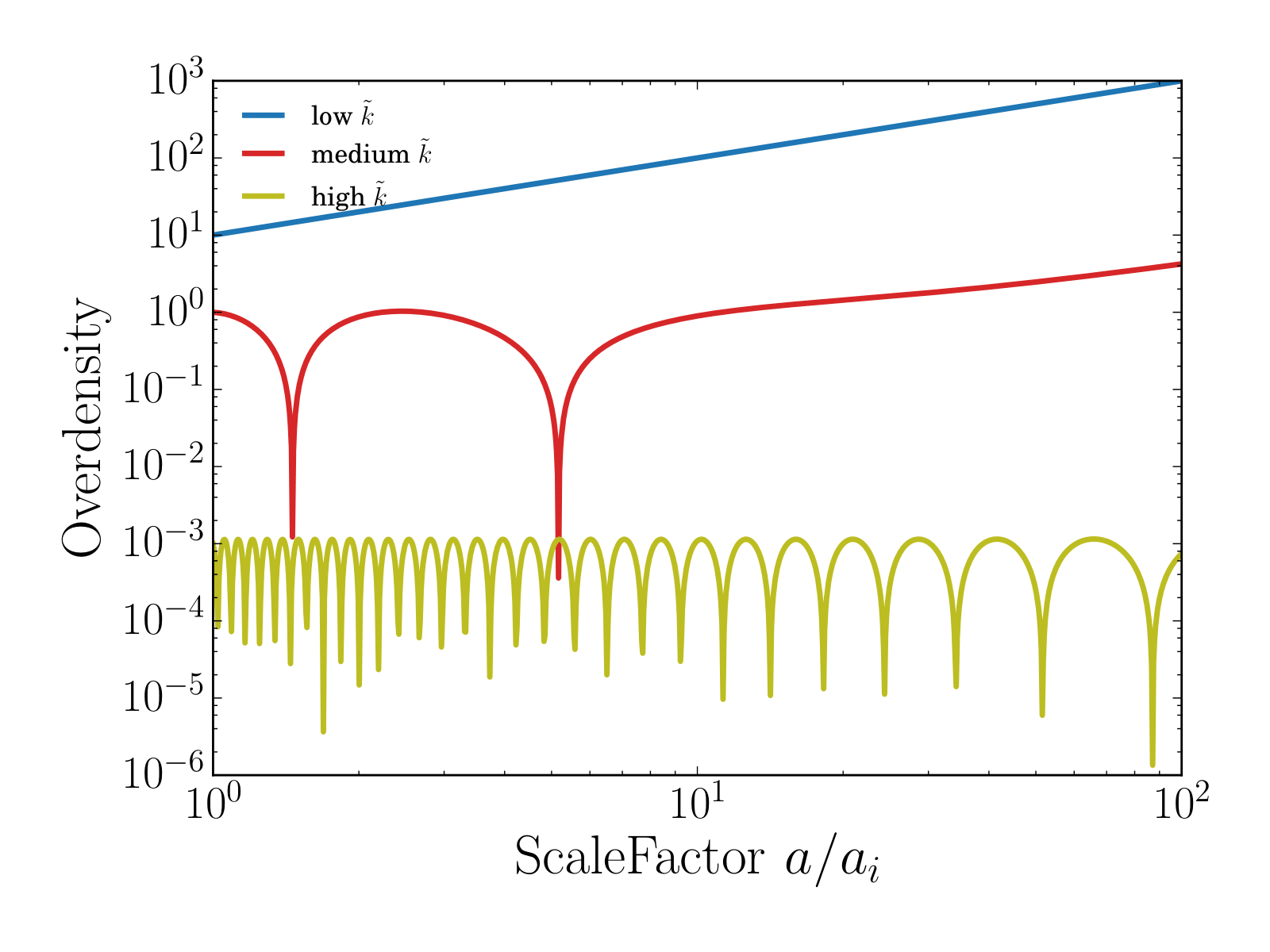
Has exact solution:
,
Fuzzy dark matter observables
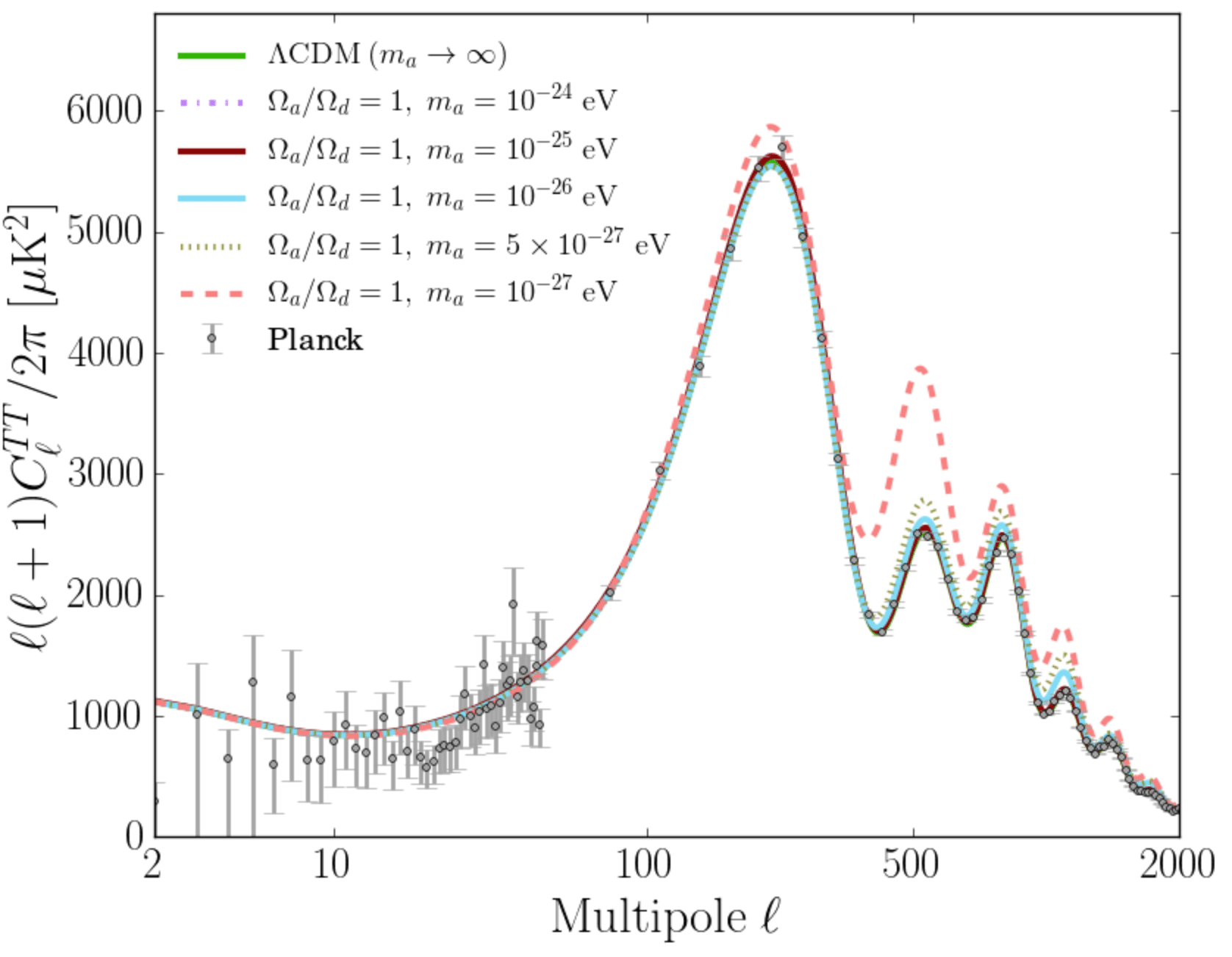
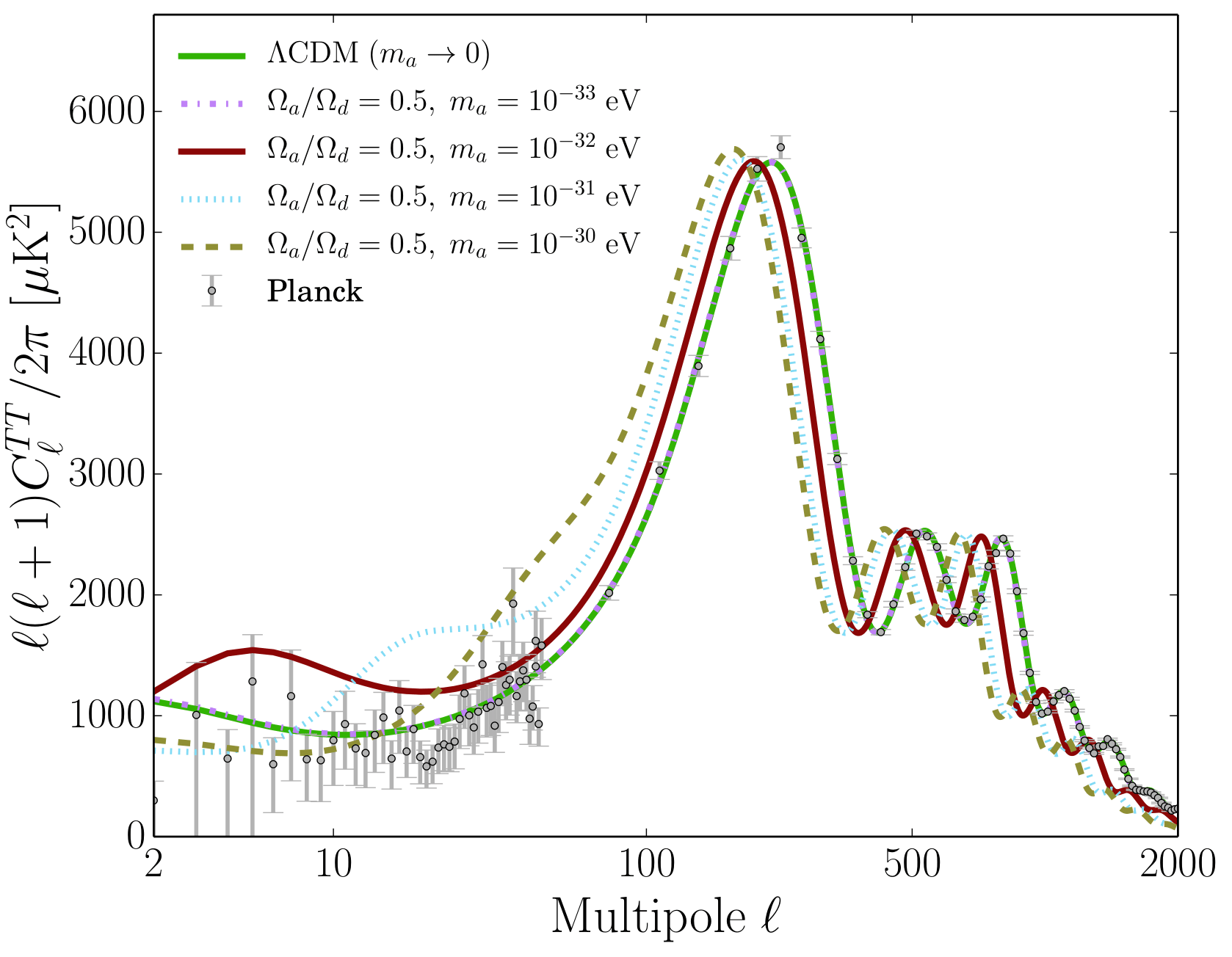
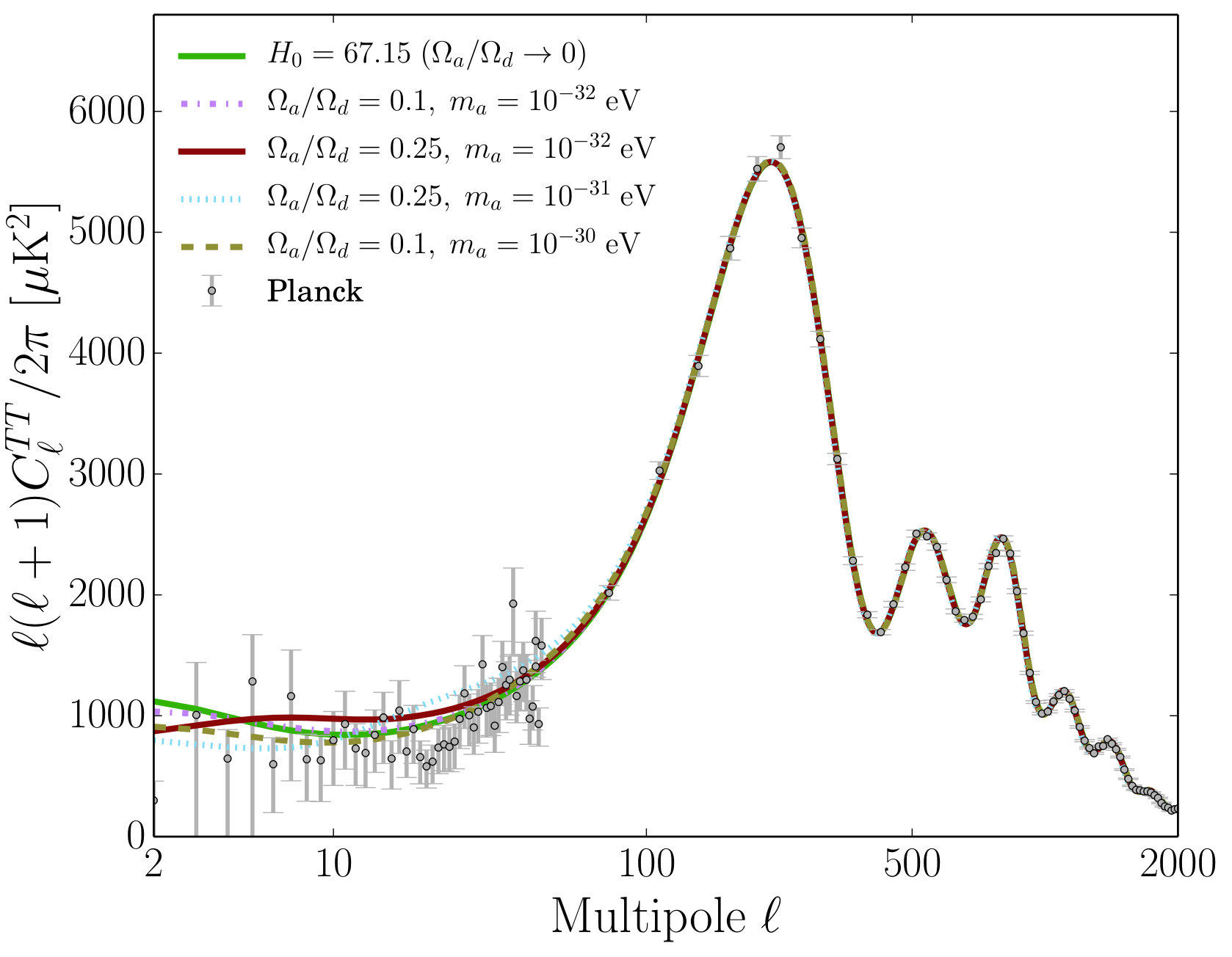
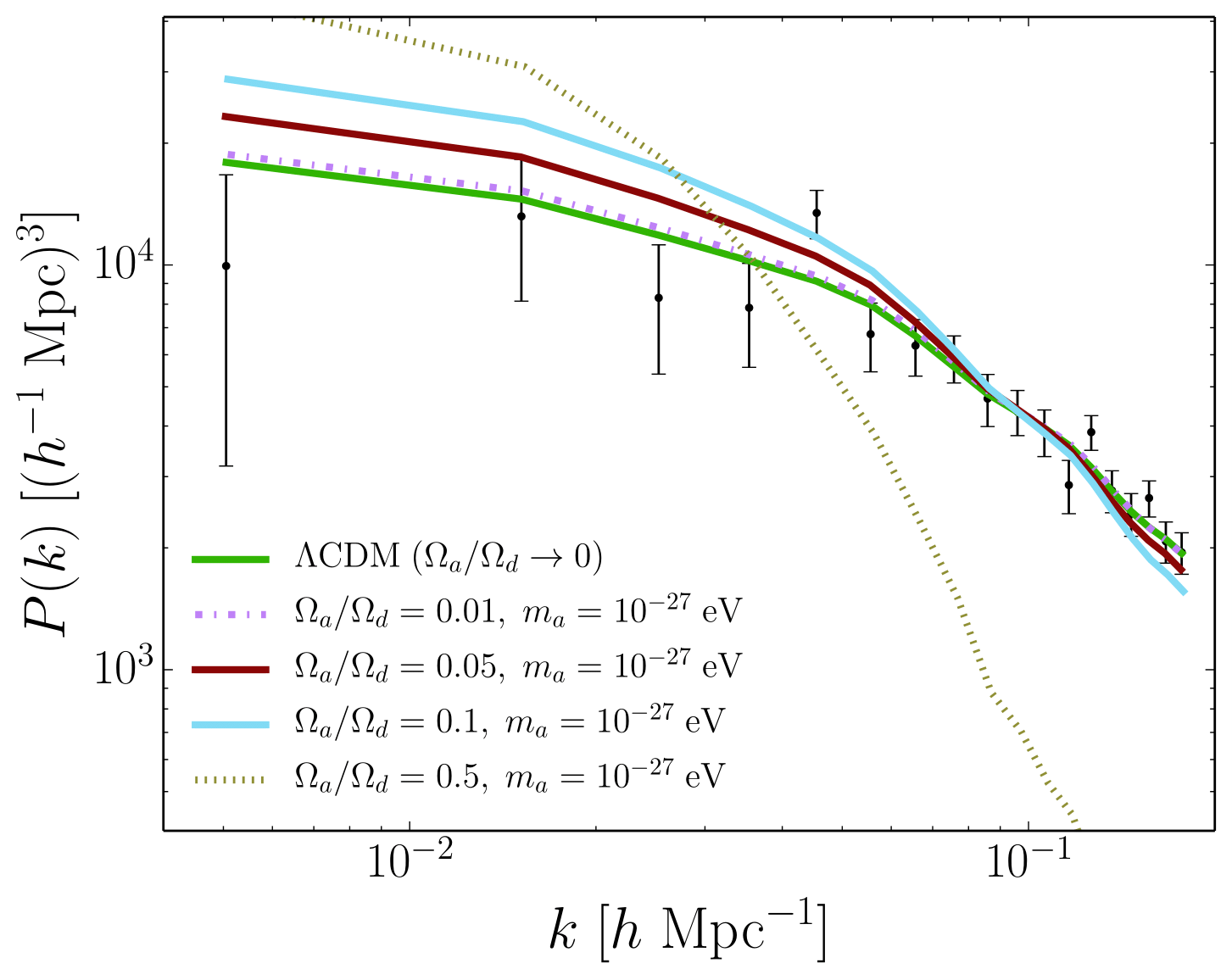
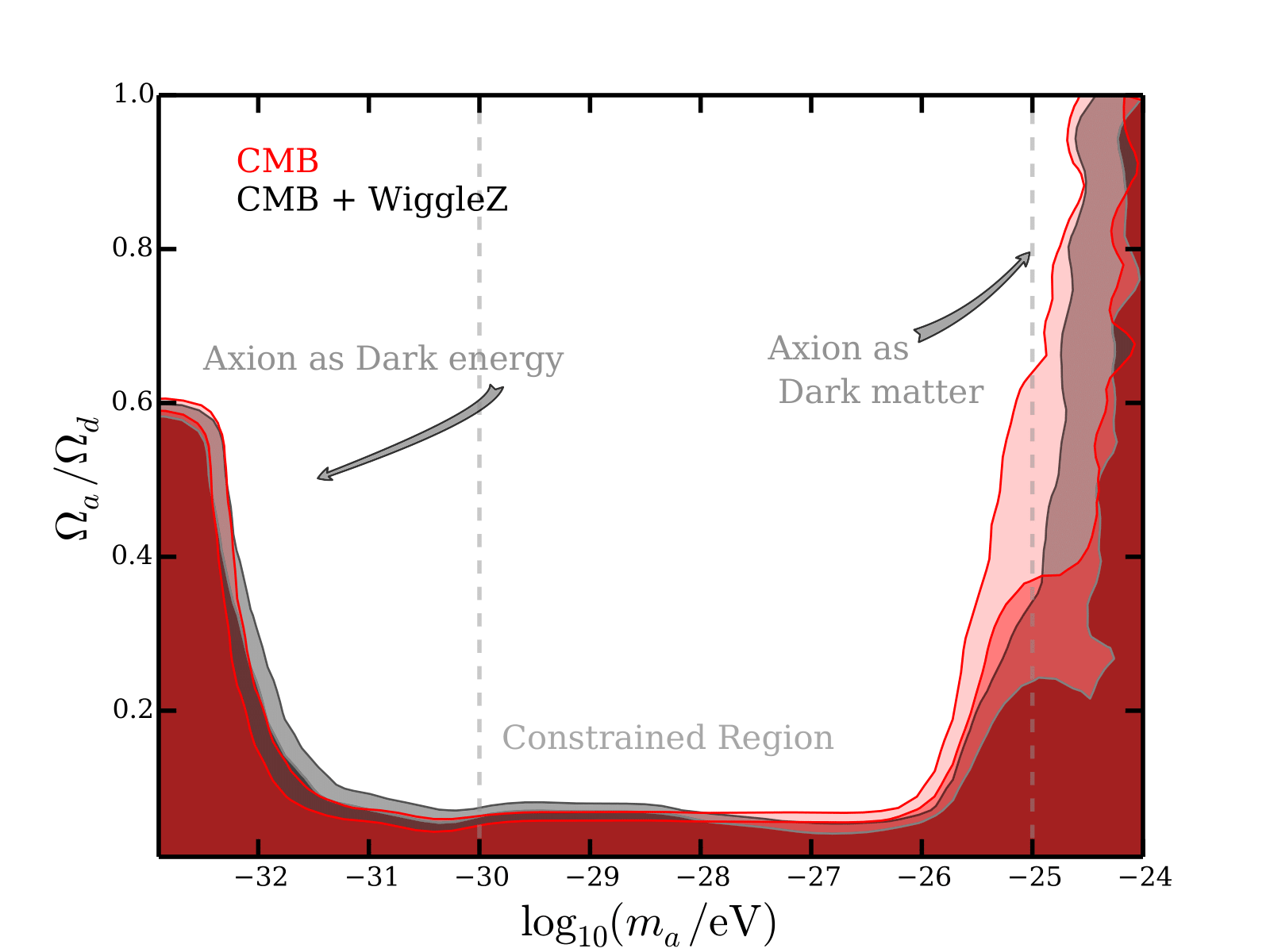
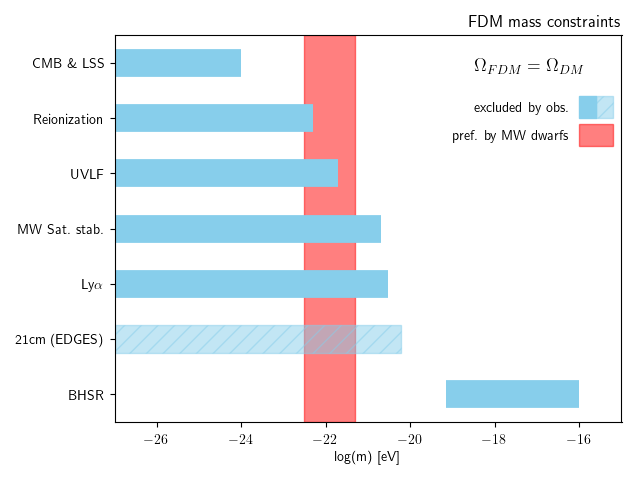
FDM mass constraints on large linear scales
[arXiv:1608.02575]
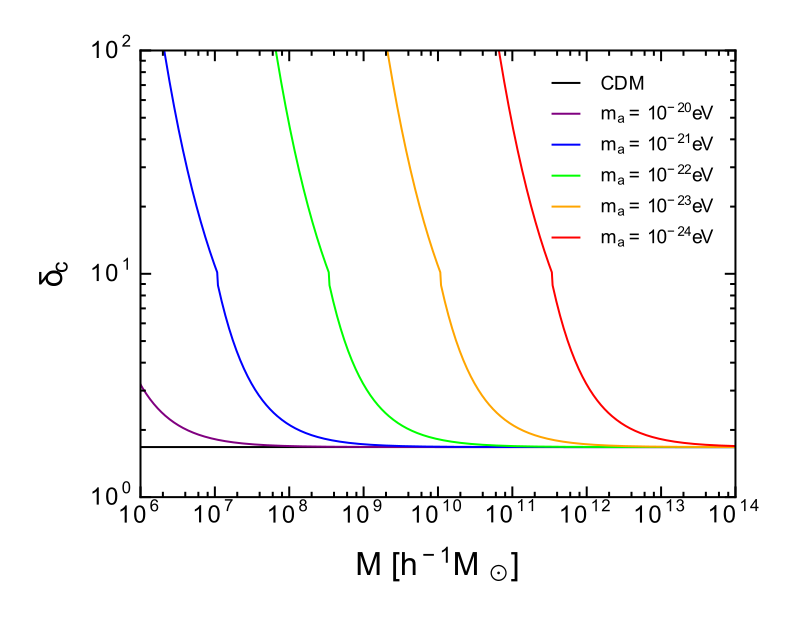
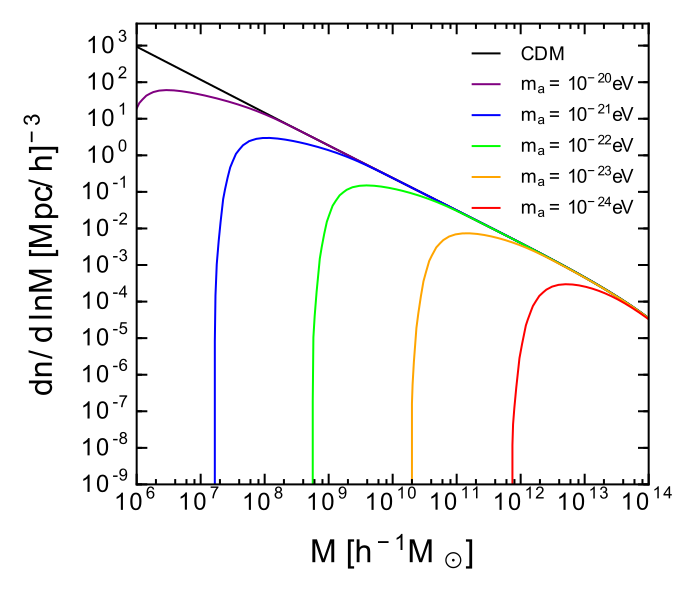
FDM mass constraints on large linear scales
Halo Mass Function is suppressed for small masses as small halos can not collapse below the deBroglie scale
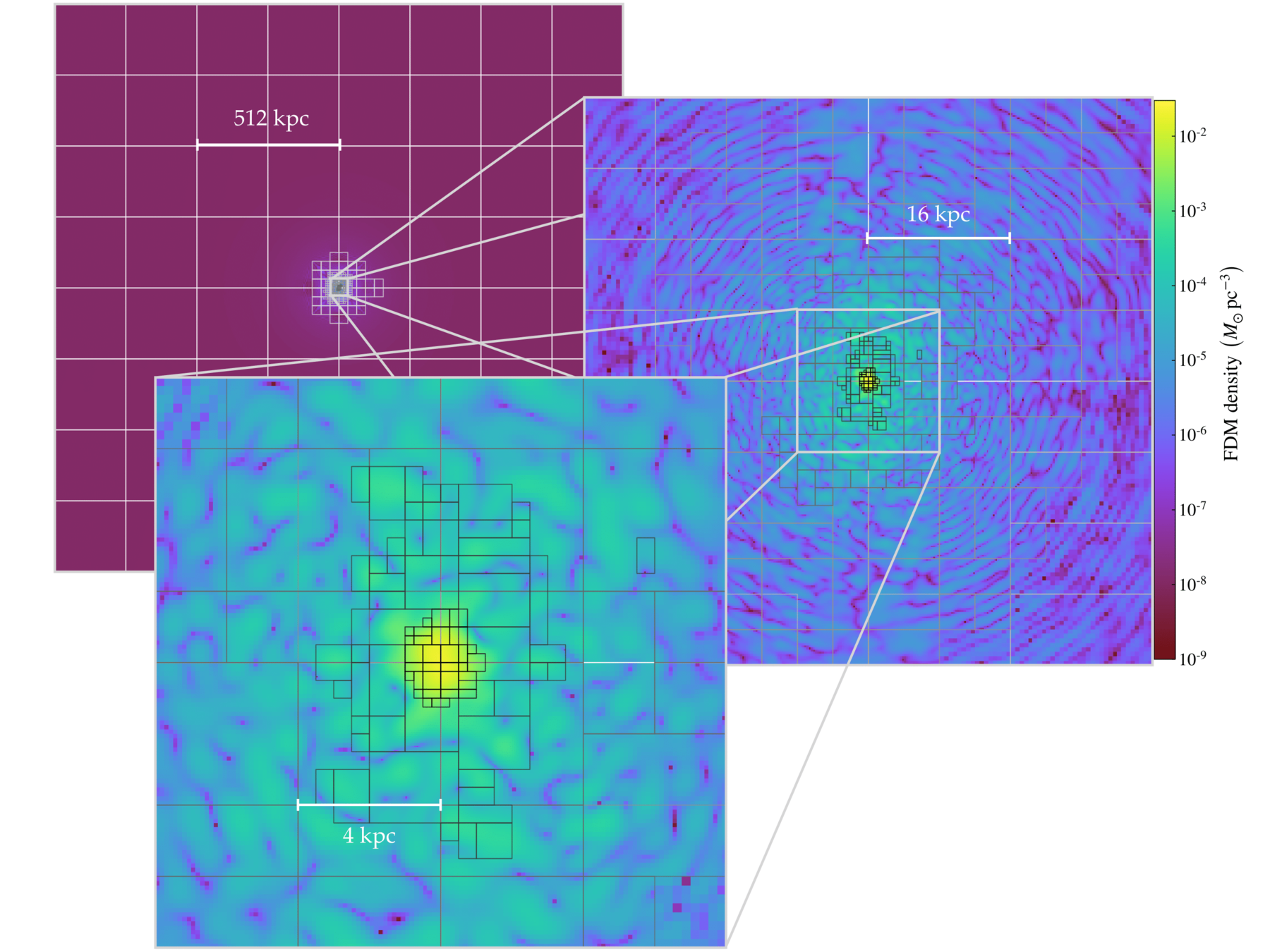
FDM halo substructure
Simulations done with AxioNyx:
Field evolved with pseudo-spectral and finite difference solver on adaptively refining mesh
[arXiv:2007.08256]
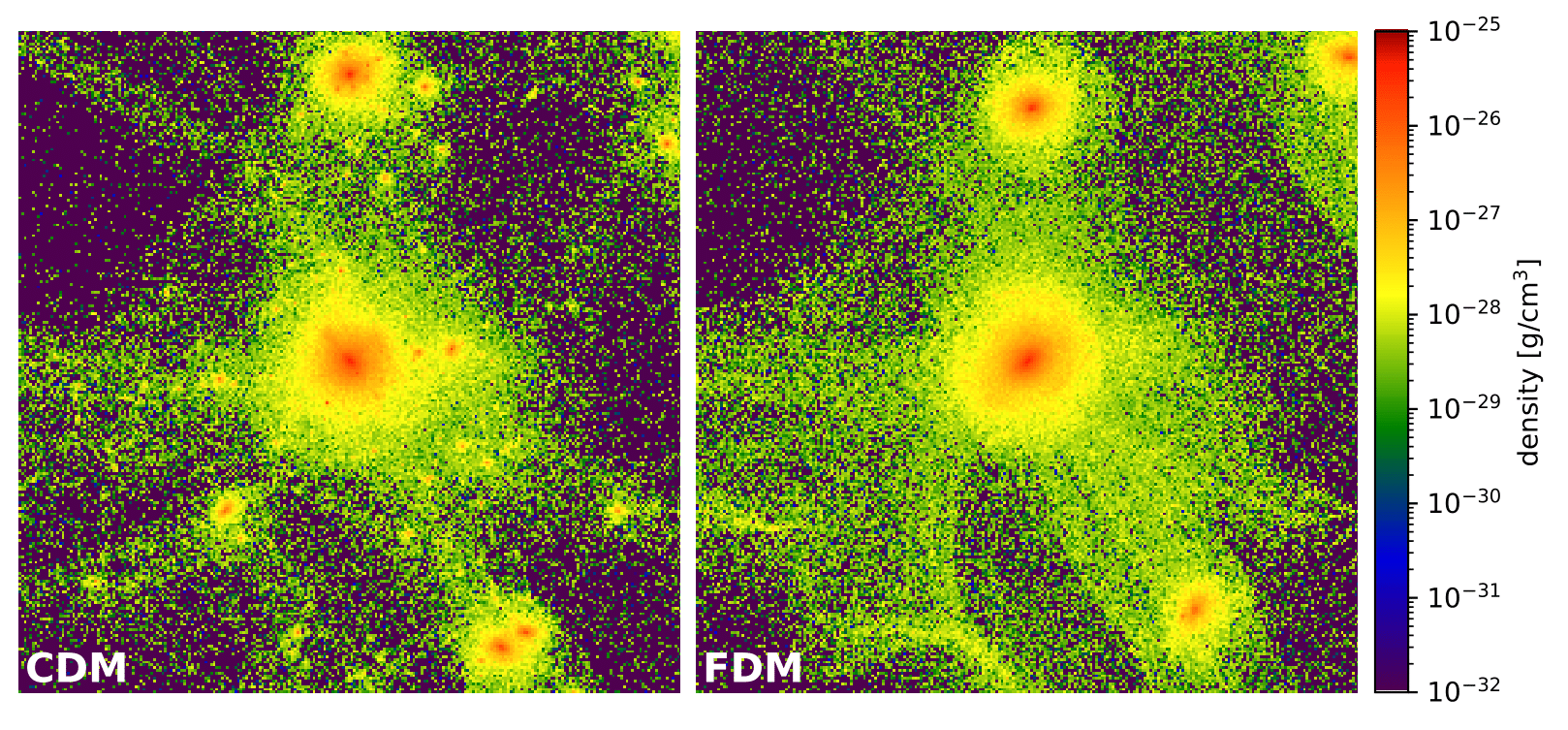
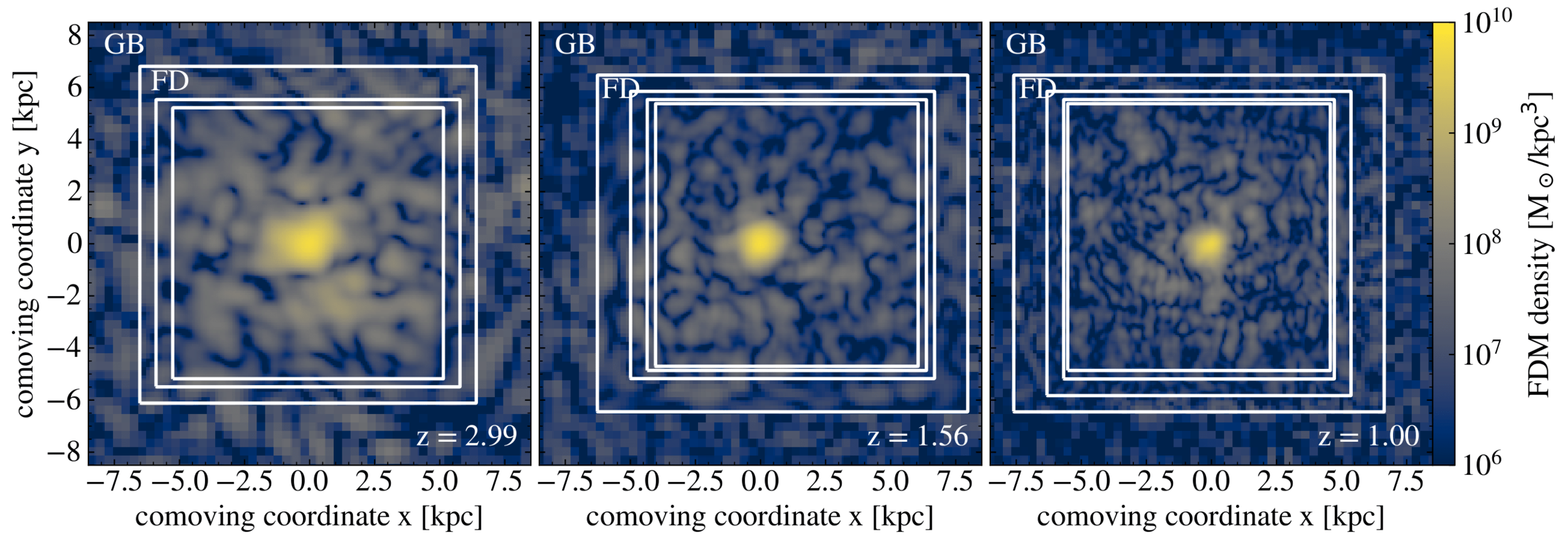
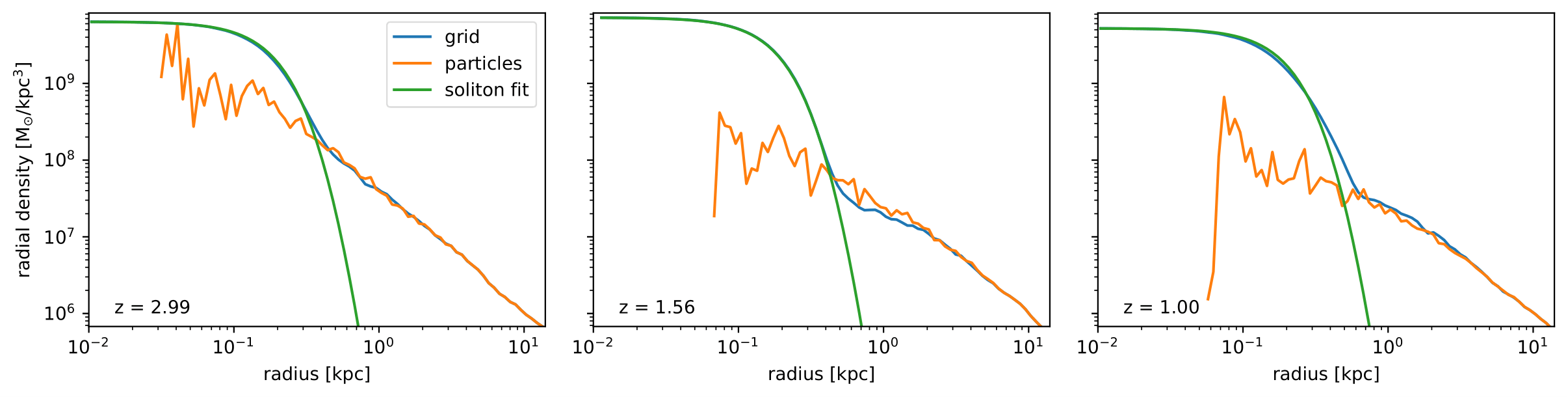
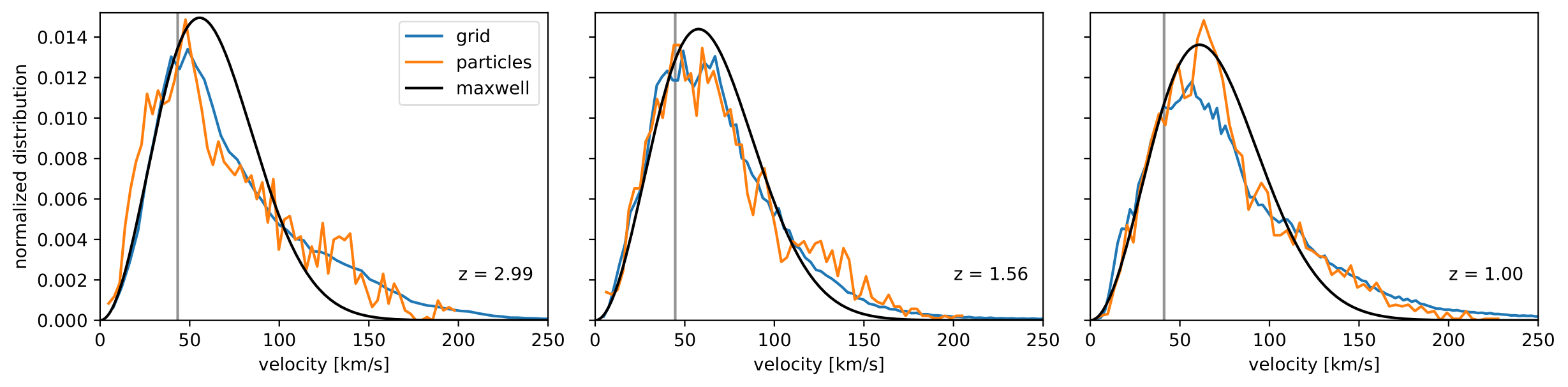
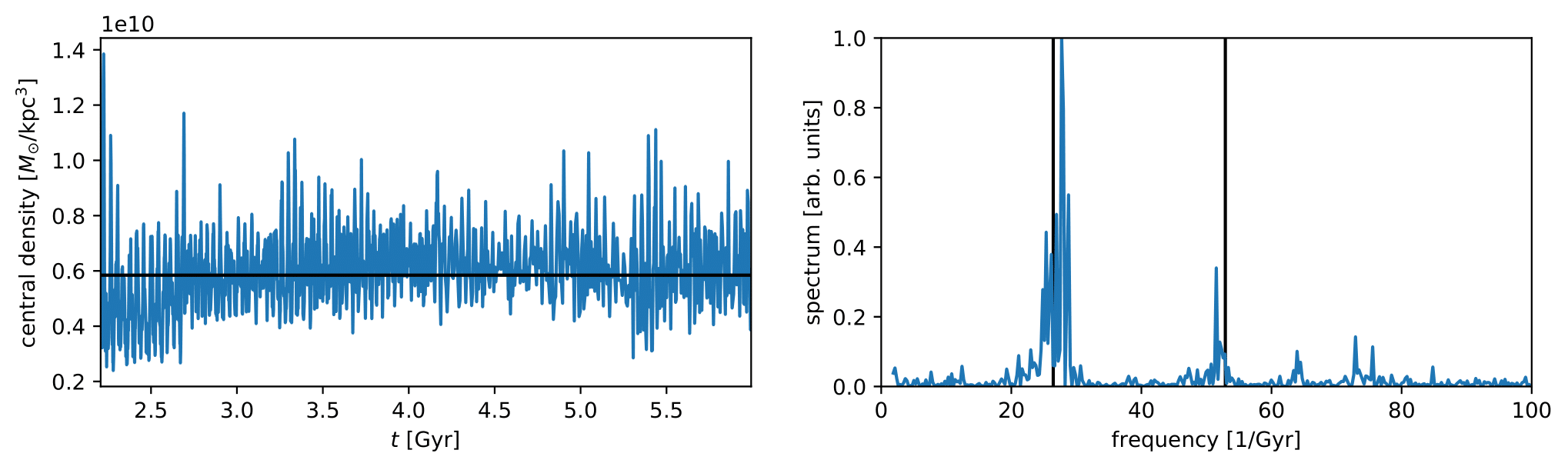
Halo substructure
[arXiv:2110.09145]
iℏ∂t∂ψ=−2ma2ℏ2∇2ψ+mVψ
i\hbar\frac{\partial\psi}{\partial t} = -\frac{\hbar^{2}}{2ma^{2}}\nabla^{2}\psi+mV\psi
∇2V=a4πGδρ
\nabla^{2}V = \frac{4\pi G}{a}\delta\rho
δρ=∣ψ∣2
\delta\rho=|\psi|^{2}
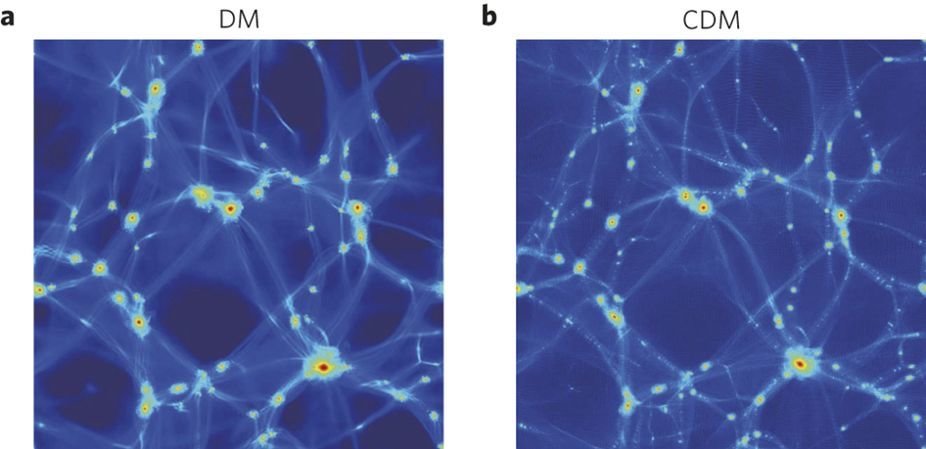
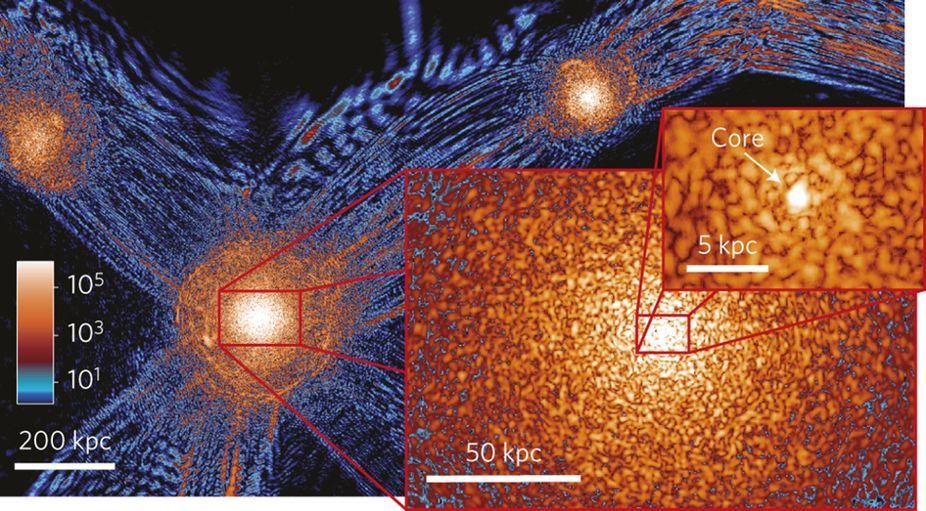
FDM Structure Formation
H.-Y. Schive, T. Chiueh, and T. Broadhurst, Nature Physics, 2014
λdB∼ℏ/mvvir∼(ℏ/m)(Gρ)−1/2r−1
\lambda_{\rm dB}\sim \hbar/mv_{\rm vir}\sim(\hbar/m)(G\rho)^{-1/2}r^{-1}
τdB∼ℏ/mvvir2
\tau_{\rm dB}\sim \hbar/mv^{2}_{\rm vir}
Lecture on FDM
By bschwabe
Lecture on FDM
- 171
