On the causal origin of the angular momentum and properties of DM halos & galaxies



With A. Pontzen & H. Peiris: 2012.02201, 2107.03407
Corentin Cadiou | JC Univers
The formation of galaxies
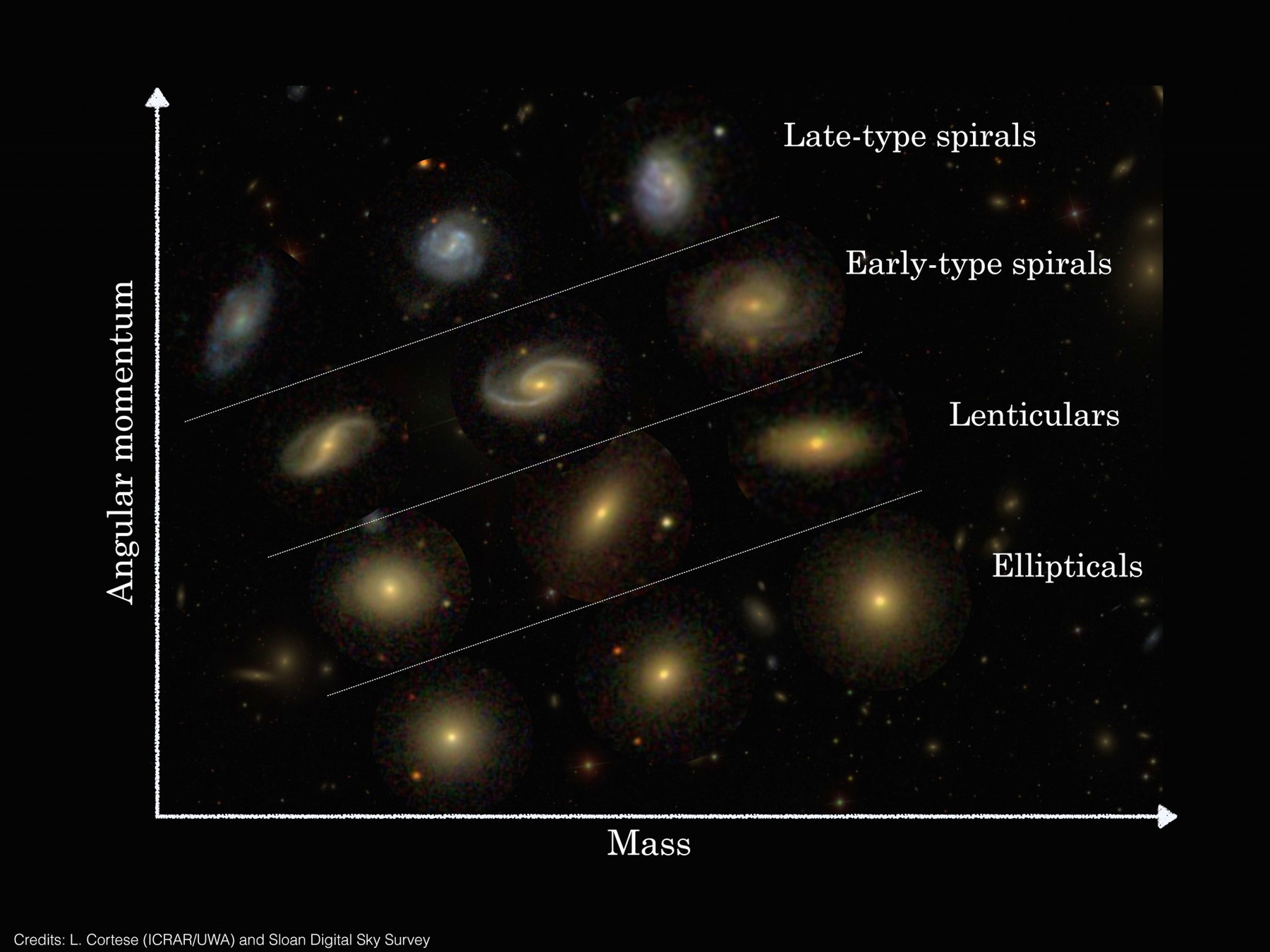
[L. Cortese; SDSS.]



[Dubois+16]
AGN no AGN
How to explain morphological diversity at fixed mass?
The formation of galaxies

[L. Cortese; SDSS.]



[Dubois+16]
AGN no AGN
How to explain morphological diversity at fixed mass?
How to explain environmental effects?

[Kraljic+ in prep]

Linking cosmology to galaxy formation: the environment
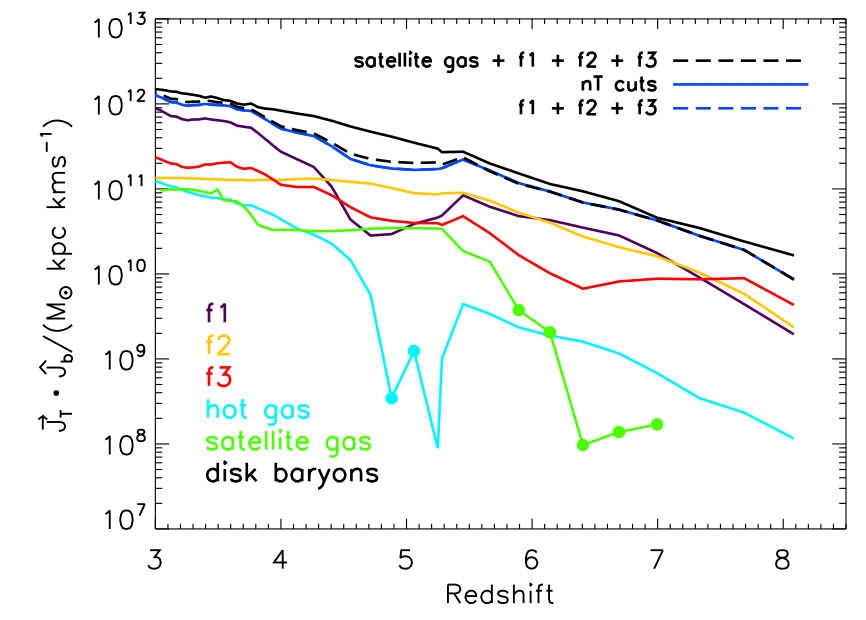
Tillson+15
High-\(z\), most of the gas + AM flows along filamentary structures…
connected to cosmic web

Cadiou+21c
[also Dekel & Birboim 06, Danovich+15]
Linking cosmology to galaxy formation: the environment



Environmental effects:
- source of “pollution” in weak lensing surveys
⇒ intrinsic alignment
- extra parameters in semi-analytical models
⇒ galaxy-halo correlation
The origin of angular momentum
Predicting angular momentum



\(z=0\)
\( z = 100\)
Predicting angular momentum



\(z=0\)
\( z = 100\)
\[\mathbf{L}_\mathrm{lin.} \propto \int\mathrm{d}^3q(\mathbf{q}-\bar{\mathbf{q}})\times \nabla\phi\]
Position w.r.t. center
Velocity
[White 84]

Predicting angular momentum



\(z=0\)
\( z = 100\)
[Genetic modifications: Roth+16, see also Rey&Pontzen 18, Stopyra+20]

Predicting angular momentum




“Tidal torque” prediction
\(N\)-body prediction






Predicting angular momentum




“Tidal torque” prediction
\(N\)-body prediction









Predicting angular momentum



- Angular momentum of individual regions can be predicted accurately.
- AM of halos ⇒ requires boundaries of patch


\[\mathbf{L}_\mathrm{lin.} \propto \int\mathrm{d}^3q(\mathbf{q}-\bar{\mathbf{q}})\times \nabla\phi\]
[On patch boundaries: see Lucie-Smith+18]
Can we control baryonic
angular momentum?
Can we control baryonic
angular momentum?

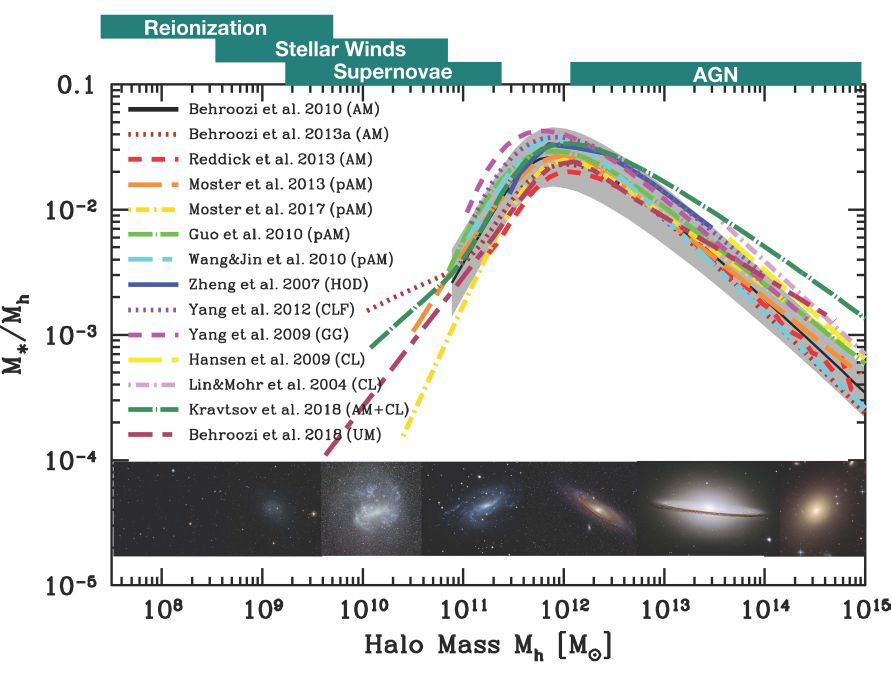
Wechsler & Tinker 18
\({\color{red}M_\star} / M_\mathrm{h} \ll \Omega_b / \Omega_m \)
⇒ baryons & DM stem from different regions


Baryons more strongly bound
⇒ less prone to being ejected



[Danovich+15]
The origin of high \(z\) angular momentum

[Danovich+15]
I. Torque with cosmic web
The origin of high \(z\) angular momentum

[Danovich+15]
I. Torque with cosmic web
II. Transport at constant AM
The origin of high \(z\) angular momentum

[Danovich+15]
I. Torque with cosmic web
II. Transport at constant AM
III. Torque down in inner halo
The origin of high \(z\) angular momentum

[Danovich+15]
I. Torque with cosmic web
II. Transport at constant AM
III. Torque down in inner halo
IV. Mixing in inner disk & bulge
The origin of high \(z\) angular momentum
The origin of high \(z\) angular momentum

[Danovich+15]
IV. Mixing in inner disk & bulge
Fraction that ends up in disk vs. IGM?
Influence of galactic physics?
III. Torque down in inner halo
Origin of torque down (pressure or gravity)?
Loss of link with cosmic AM?
II. Transport at constant AM
Same evolution in cold/hot accretion modes?
I. Torque with cosmic web
Predict pre-accretion AM?
Alignment with environment?
The origin of high \(z\) angular momentum

[Danovich+15]
IV. Mixing in inner disk & bulge
Fraction that ends up in disk vs. IGM?
Influence of galactic physics?
III. Torque down in inner halo
Origin of torque down (pressure or gravity)?
Loss of link with cosmic AM?
See Cadiou+21c
II. Transport at constant AM
Same evolution in cold/hot accretion modes?
I. Torque with cosmic web
Predict pre-accretion AM?
Alignment with environment?
The origin of high \(z\) angular momentum

[Danovich+15]
IV. Mixing in inner disk & bulge
Fraction that ends up in disk vs. IGM?
Influence of galactic physics?
III. Torque down in inner halo
Origin of torque down (pressure or gravity)?
Loss of link with cosmic AM?
II. Transport at constant AM
Same evolution in cold/hot accretion modes?
I. Torque with cosmic web
Predict pre-accretion AM?
Alignment with environment?
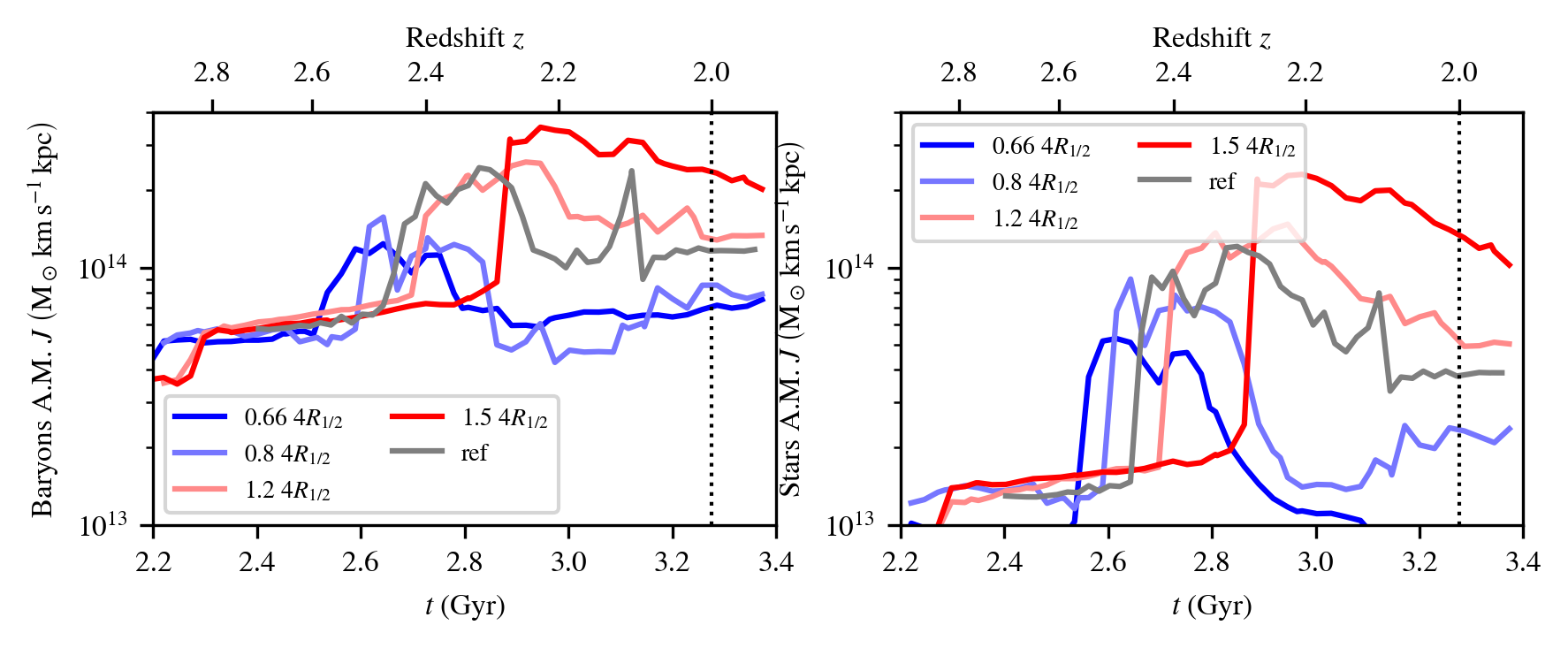
Baryon angular momentum
Simulations (9Mh @ DiRAC):
- Resolve disk height
\(\Delta x = 35\ \mathrm{kpc}\) - \(z \geq 2\), \(M_\mathrm{200c} = 10^{12}\ \mathrm{M}_\odot\)
- SF + AGN & SN feedback
- Modify \(l(z=2)\)
-
Tracer particles
Cadiou+19
\( l_0 \times 0.66\)
\( l_0 \times 0.8\)
\( l_0 \times 1.2\)
\( l_0 \times 1.5\)

\( l_0 \times 1.2\)
\( l_0 \times 1.5\)

\( l_0 \times 0.66\)
\( l_0 \times 0.8\)
\( l_0 \times 0.66\)
\( l_0 \times 0.8\)
\( l_0 \times 1.2\)
\( l_0 \times 1.5\)


+

Angular momentum of the baryons / stars within \(R_\mathrm{vir}\)





+

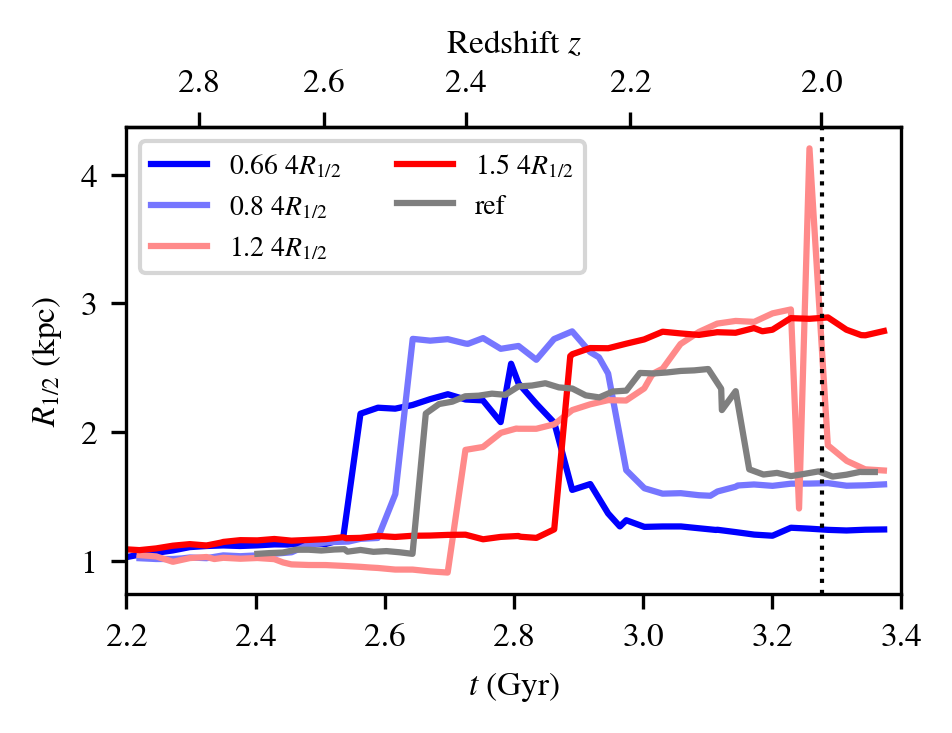
\( R_{1/2} \)
\( l_0 \times 1.2\)
\( l_0 \times 1.5\)

\( l_0 \times 0.66\)
\( l_0 \times 0.8\)

\( l_0 \times 0.66\)
\( l_0 \times 0.8\)
\( l_0 \times 1.2\)
\( l_0 \times 1.5\)

- AM of baryons can be controlled!
- ≠ effect on stars / baryons
- Observables are impacted (significantly!)
-
Little AGN/SN global self-regulation
- formation of blue nuggets?
- co-evolution \(l - M_\bullet \)?
- create “spin-flips”?
- …

\( R_{1/2} \)
\( l_0 \times 1.2\)
\( l_0 \times 1.5\)

\( l_0 \times 0.66\)
\( l_0 \times 0.8\)

\( l_0 \times 0.66\)
\( l_0 \times 0.8\)
\( l_0 \times 1.2\)
\( l_0 \times 1.5\)
Temporary conclusions
-
angular momentum is predictable
-
boundary of halos in the ICs is a hard problem
⇒ limits practicality of predictions (for now)
-
baryons appear to be simpler!
⇒ good news for weak lensing predictions
⇒ also good news for my DiRAC project
-
but why do some objects grow their AM faster/slower?



The effect of environment on halo properties
The effect of environment on halo properties
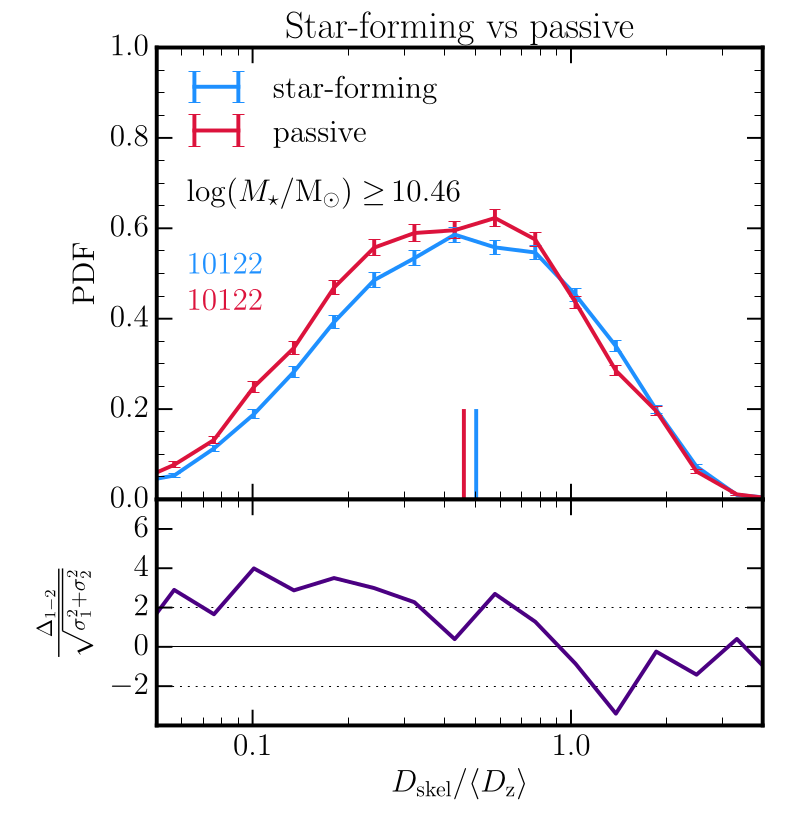
Distance to filament
Kraljic+18 [see also Laigle15, Song+21,…]


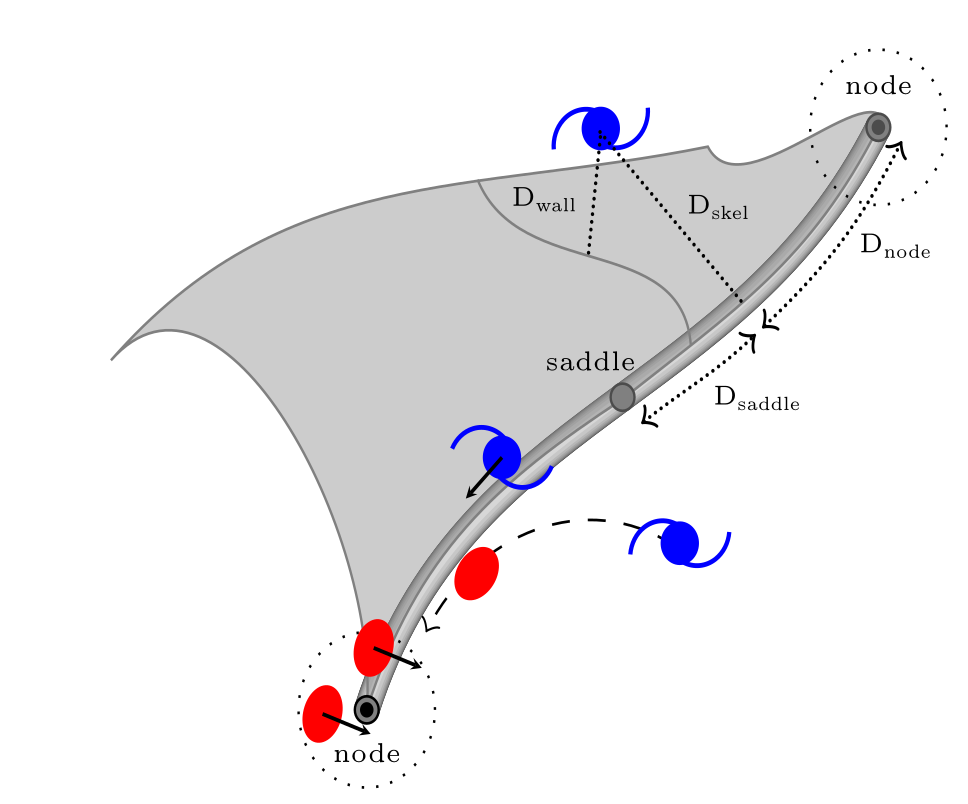





What if the galaxy had formed here instead?




What if the galaxy had formed here instead?


or here?
The “splicing” technique


- Generate ICs
- Integrate (\(N\)-nody)
- Select region of interest
- Trace back to ICs
- “Splice”
- Integrate again

\(t\)

Splicing: equivalent of constraining field at all points in spliced region
Splicing in 1D





Splicing in 1D


Most likely* field \(f\) with
- same value in spliced region (\(a\)),
- as close as possible outside (\(b\))



Mathematically \(f\) is solution of:
\( f= a\) in \(\Gamma\)
minimizes \(\mathcal{Q} = (b-f)^\dagger\mathbf{C}^{-1}(b-f) \) outside \(\Gamma\)
The causal origin of DM halo concentration
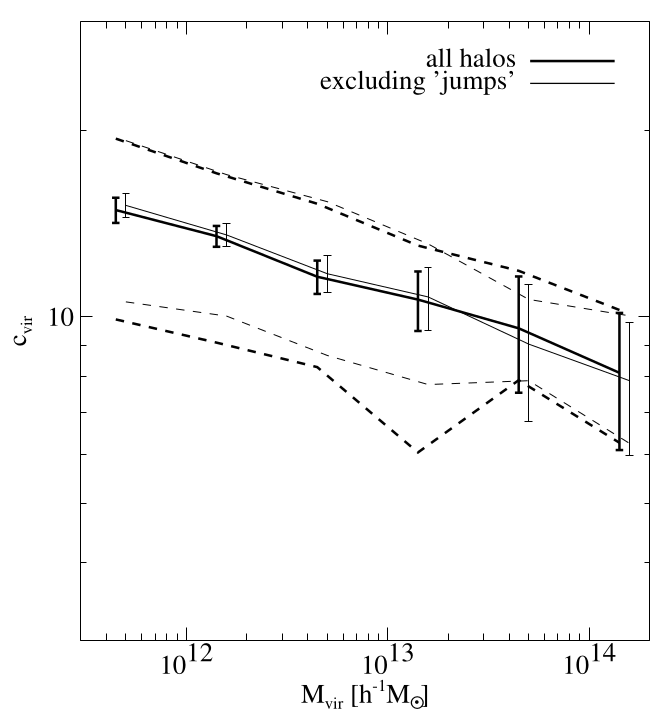

$$\rho_\mathrm{DM}(r) = \frac{\rho_0}{\frac{r}{R_\mathrm{vir}/c} \left(1 + \frac{r}{R_\mathrm{vir}/c}\right)^2}$$
Wechsler+02
Origin of scatter at fixed \(M_\mathrm{vir}\)?
The causal origin of DM halo concentration


\(M^{(1)}_{200\mathrm{c}}, c^{(1)}_\mathrm{NFW}, \dots\)


\(M^{(2)}_{200\mathrm{c}}, c^{(2)}_\mathrm{NFW}, \dots\)


\(M^{(\dots)}_{200\mathrm{c}}, c^{(\dots)}_\mathrm{NFW}, \dots\)


\(M^{(10)}_{200\mathrm{c}}, c^{(10)}_\mathrm{NFW}, \dots\)
Same halo in 10× different environments
Repeat experiment for 7 halos (70 realisations in total)
Same halo in 10× different environments
Repeat experiment for 7 halos (70 realisations in total)


\(M^{(1)}_{200\mathrm{c}}, c^{(1)}_\mathrm{NFW}, \dots\)


\(M^{(2)}_{200\mathrm{c}}, c^{(2)}_\mathrm{NFW}, \dots\)


\(M^{(\dots)}_{200\mathrm{c}}, c^{(\dots)}_\mathrm{NFW}, \dots\)


\(M^{(10)}_{200\mathrm{c}}, c^{(10)}_\mathrm{NFW}, \dots\)

The causal origin of DM halo concentration
Same halo in 10× different environments
Repeat experiment for 7 halos (70 realisations in total)


\(M^{(1)}_{200\mathrm{c}}, c^{(1)}_\mathrm{NFW}, \dots\)


\(M^{(2)}_{200\mathrm{c}}, c^{(2)}_\mathrm{NFW}, \dots\)


\(M^{(\dots)}_{200\mathrm{c}}, c^{(\dots)}_\mathrm{NFW}, \dots\)


\(M^{(10)}_{200\mathrm{c}}, c^{(10)}_\mathrm{NFW}, \dots\)



The causal origin of DM halo concentration
50% of population
Conclusion & outlook
Conclusion & outlook
-
angular momentum is predictable
-
boundary of halos in the ICs is a hard problem
⇒ limits practicality of predictions (for now)
-
baryons can be controlled!
⇒ good news for weak lensing predictions
stay tuned!
-
environmental effects can have dramatic impact on halo formation
⇒ 50% of concentration scatter due to env.
⇒ similar impact on galaxy formation?




Conclusion & outlook




Questions?
More infos in Cadiou+21a,b,c (2012.02201, 2107.03407, 2110.05384)
-
angular momentum is predictable
-
boundary of halos in the ICs is a hard problem
⇒ limits practicality of predictions (for now)
-
baryons can be controlled!
⇒ good news for weak lensing predictions
stay tuned!
-
environmental effects can have dramatic impact on halo formation
⇒ 50% of concentration scatter due to env.
⇒ similar impact on galaxy formation?

Verify that
\[\xi_\mathrm{lin}(r) \sim \left\langle {\color{green}\underbrace{\delta(x=d)}_\mathrm{in}} {\color{purple} \underbrace{\delta(x=d+r)}_\mathrm{out}}\right\rangle \]
is the same in spliced / ref simulation.

Verify that
\[\xi_\mathrm{lin}(r) \sim \left\langle {\color{green}\underbrace{\delta(x=d)}_\mathrm{in}} {\color{purple} \underbrace{\delta(x=d+r)}_\mathrm{out}}\right\rangle \]
is the same in spliced / ref simulation.

Verify that
\[\xi_\mathrm{lin}(r) \sim \left\langle {\color{green}\underbrace{\delta(x=d)}_\mathrm{in}} {\color{purple} \underbrace{\delta(x=d+r)}_\mathrm{out}}\right\rangle \]
is the same in spliced / ref simulation.

On the causal origin of the angular momentum and properties of DM halos & galaxies
By Corentin Cadiou
On the causal origin of the angular momentum and properties of DM halos & galaxies
- 373



