Corentin Cadiou
IAP symposium
13/12/23

The causal origin of galactic angular momentum:
replacing galaxies in their cosmological context
With Z. Kocjan, A. Storck, E. Pichon-Pharabod, Agertz, Dubois, Peiris, Pontzen, Pichon, Pogosyan, …
Cadiou, Pontzen & Peiris 21 · Cadiou, Pontzen +21 · Kocjan, Cadiou, Agertz, Pontzen 23 · Cadiou, Pichon-Pharabod+23
Angular momentum: bridging galaxy formation to cosmology

2 Spin \(\leftrightarrow\) morphology
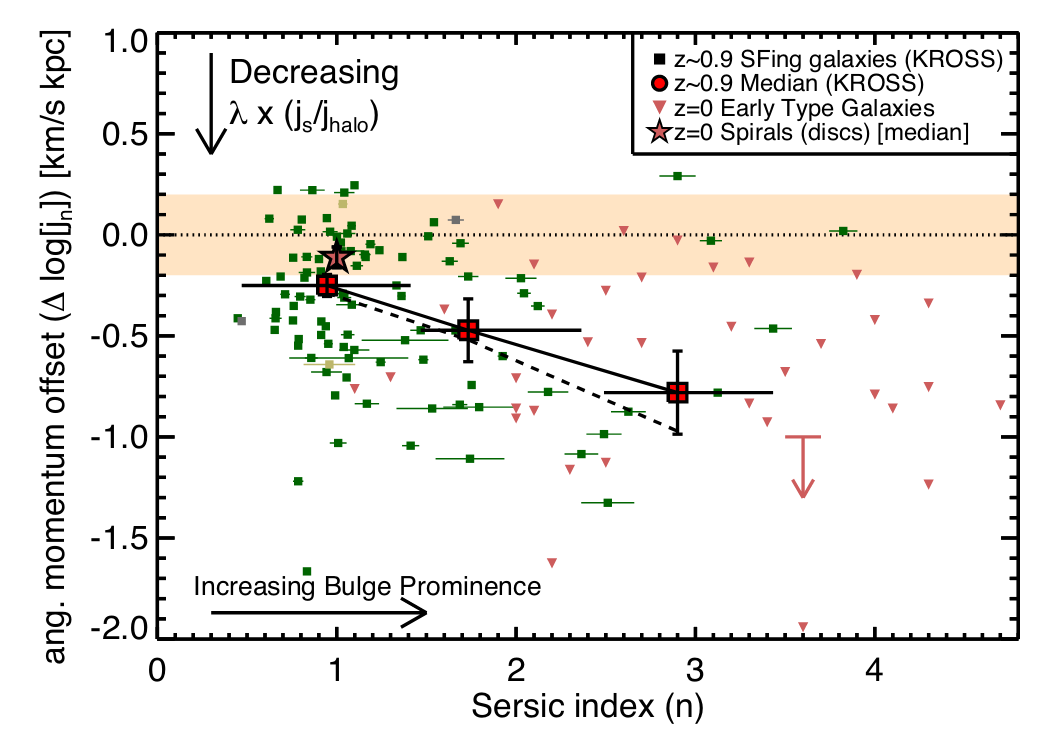
Romanowsky&Fall 12
Harrison+17
Hasan+23 (TNG)
3 Cosmic web \(\leftrightarrow\) SFR
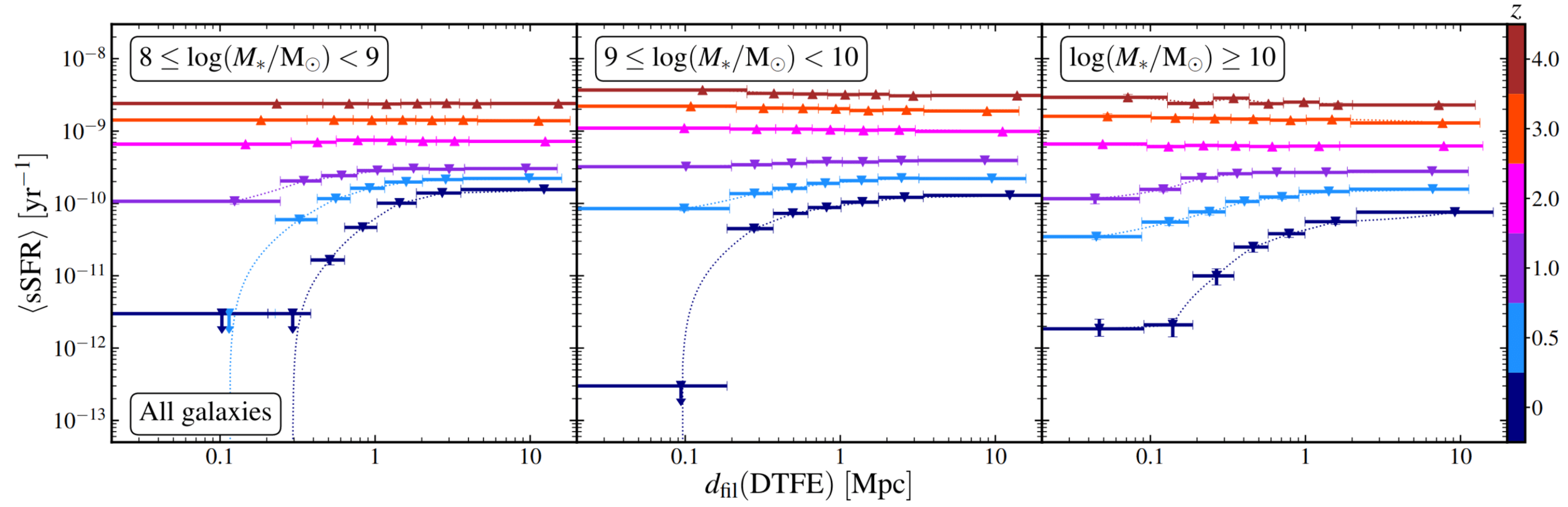

Kraljic+CC+19 (HAGN)
1 Cosmic web \(\leftrightarrow\) spin

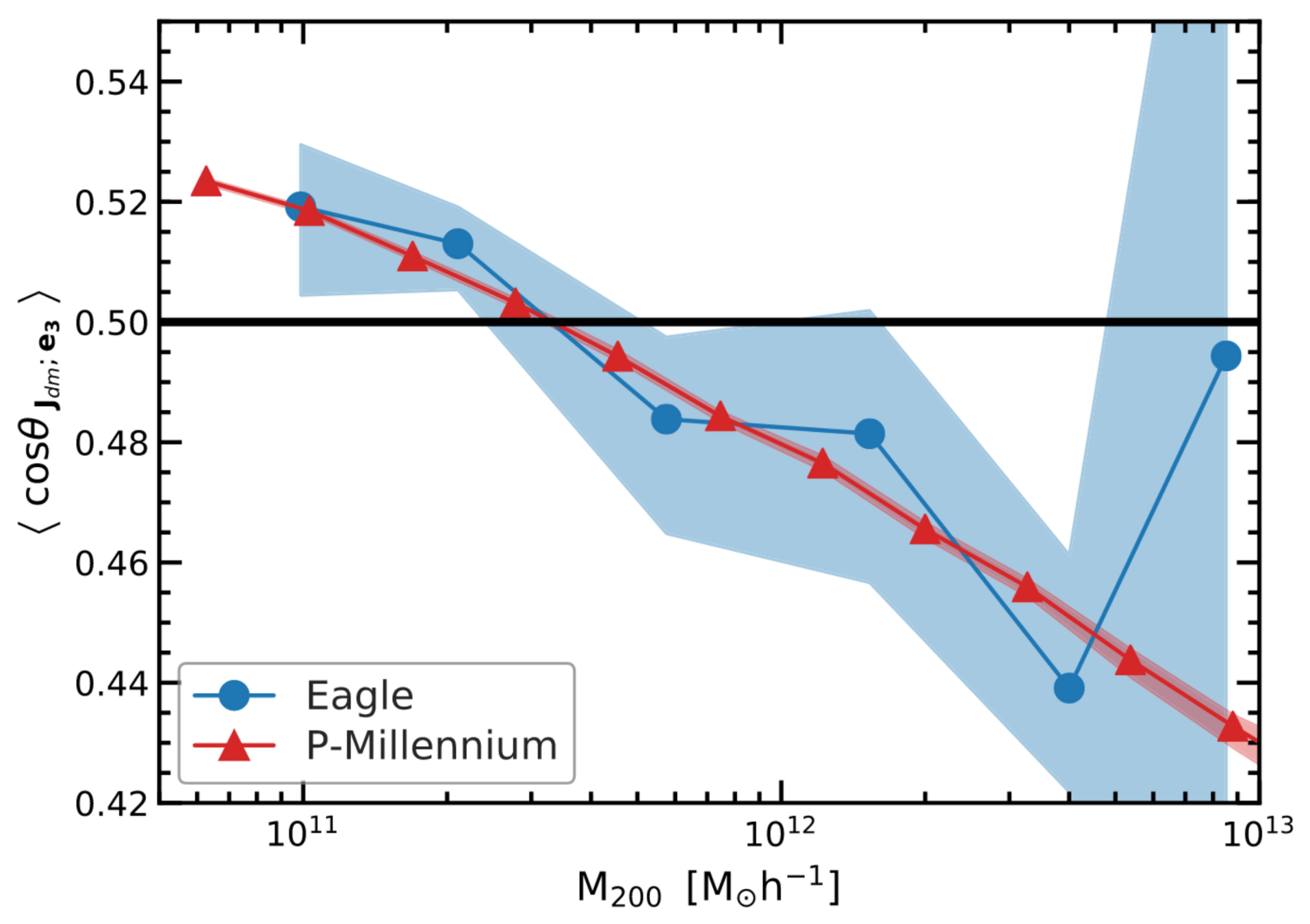
1 Cosmic web \(\leftrightarrow\) spin
Ganeshaiah Veena+21
Corentin Cadiou
Angular momentum: bridging galaxy formation to cosmology

2 Spin \(\leftrightarrow\) morphology

Romanowsky&Fall 12
Harrison+17
Hasan+23 (TNG)

3 Cosmic web \(\leftrightarrow\) SFR


Kraljic+CC+19 (HAGN)
1 Cosmic web \(\leftrightarrow\) spin


1 Cosmic web \(\leftrightarrow\) spin
Ganeshaiah Veena+21
Corentin Cadiou
- Why is the effect of the cosmic web at % level?
- What's the arrow of causality?
CW ⇒ spin ⇒ morphology? - How stochastic is galaxy formation?
MEGATRON
Rey, Katz & Cadiou in prep
- Large volumes (TNG, HAGN, …)
- statistical results only
- relatively poor resolution
- Small volumes & zoom-ins
- few formation scenarios
- Genetically modified simulations
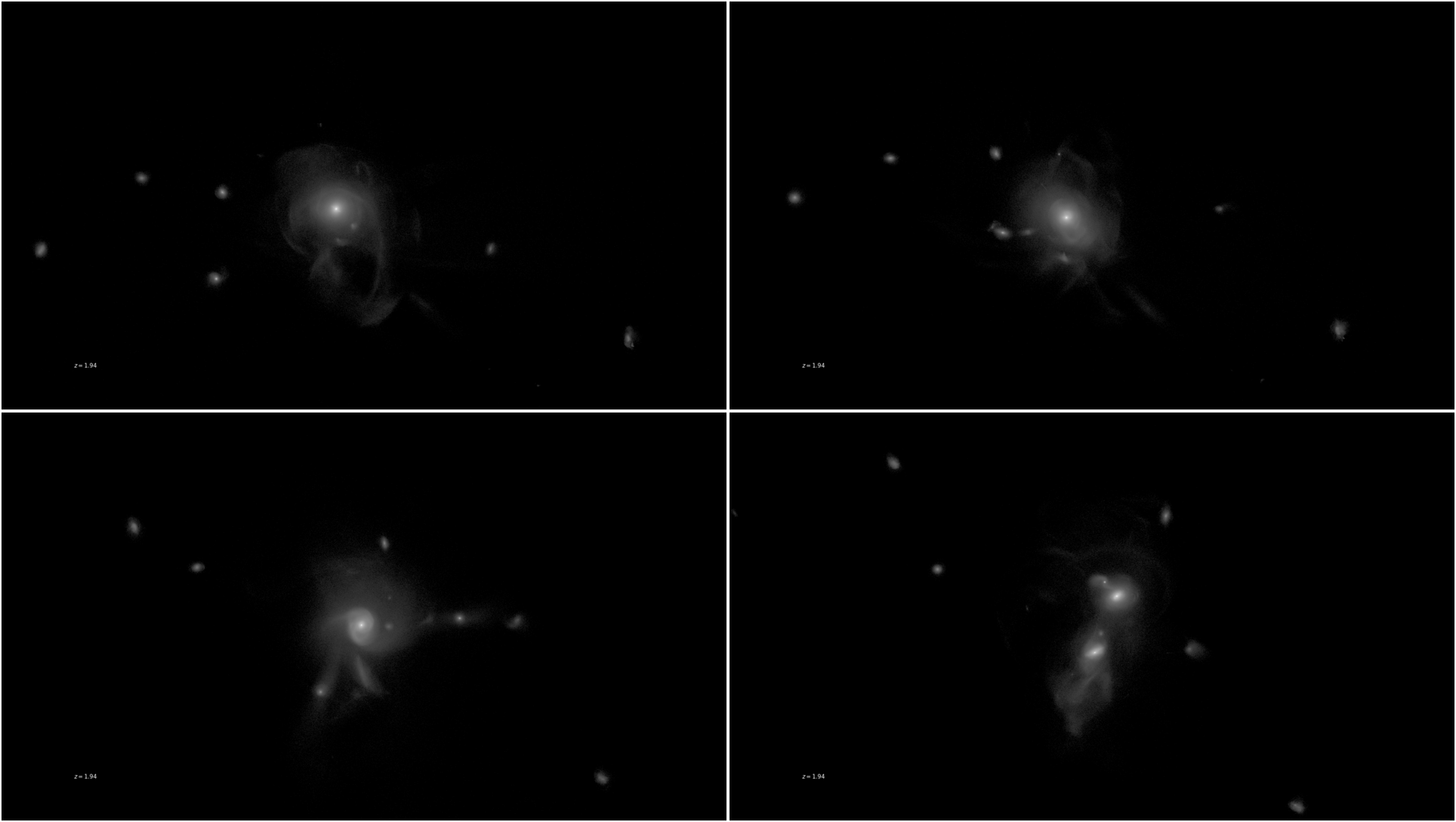
tides ×0.5 ⇒ merger @ \(z=0.7\)
tides ×1.1 ⇒ merger @ \(z=0.55\)
tides ×1.2 ⇒ merger @ \(z=0.5\)
tides ×2 ⇒ merger @ \(z=0.2\)
Changes to tides at \(z=100\), effect at \(z<1\)
Unraveling the origin of baryonic angular momentum
Full hydro simulations
(10Mh @ DiRAC):
- Resolve disk height
\(\Delta x_\mathrm{min} = 35\ \mathrm{pc}\) - \(M_\mathrm{200c} = 10^{12}\ \mathrm{M}_\odot\) @ \(z=2\)
- SF + AGN & SN feedback
- 3 galaxies, 5× scenario each
\( j_0 \times 0.66\)
\( j_0 \times 0.8\)
\( j_0 \times 1.2\)
\( j_0 \times 1.5\)
Corentin Cadiou


INPUT: Changes to tides \(z=\infty\)
OUTPUT: Ang. mom
\(z=2\)
\( j_0 \times 0.66\)
\( j_0 \times 0.8\)
\( j_0 \times 1.2\)
\( j_0 \times 1.5\)
\( j_0 \times 0.66\)
\( j_0 \times 0.8\)
\( j_0 \times 1.2\)
\( j_0 \times 1.5\)

See Cadiou, Pontzen & Peiris+21
Corentin Cadiou



\( j_0 \times 0.66\)
\( j_0 \times 0.8\)
\( j_0 \times 1.2\)
\( j_0 \times 1.5\)
\( j_0 \times 0.66\)
\( j_0 \times 0.8\)
\( j_0 \times 1.2\)
\( j_0 \times 1.5\)

See Cadiou, Pontzen & Peiris+21
INPUT: Changes to tides \(z=\infty\)
OUTPUT: Ang. mom
\(z=2\)
Corentin Cadiou


Stellar disk angular momentum responds ~linearly to large-scale tides
See Cadiou, Pontzen & Peiris+21
INPUT: Changes to tides \(z=\infty\)
OUTPUT: Ang. mom
\(z=2\)
Corentin Cadiou

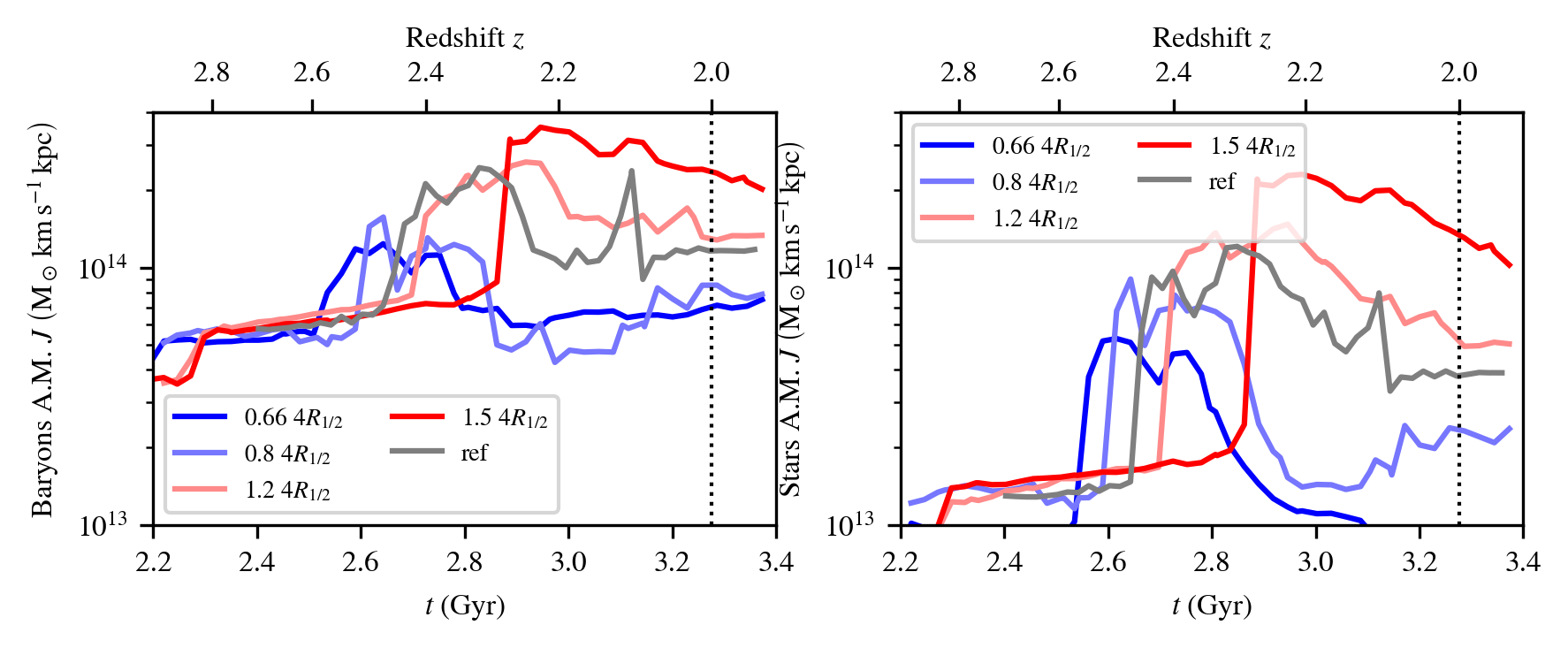
Gas + stars spAM
Stars spAM
Halo spAM
Halo spAM
See Cadiou, Pontzen & Peiris+21
Corentin Cadiou
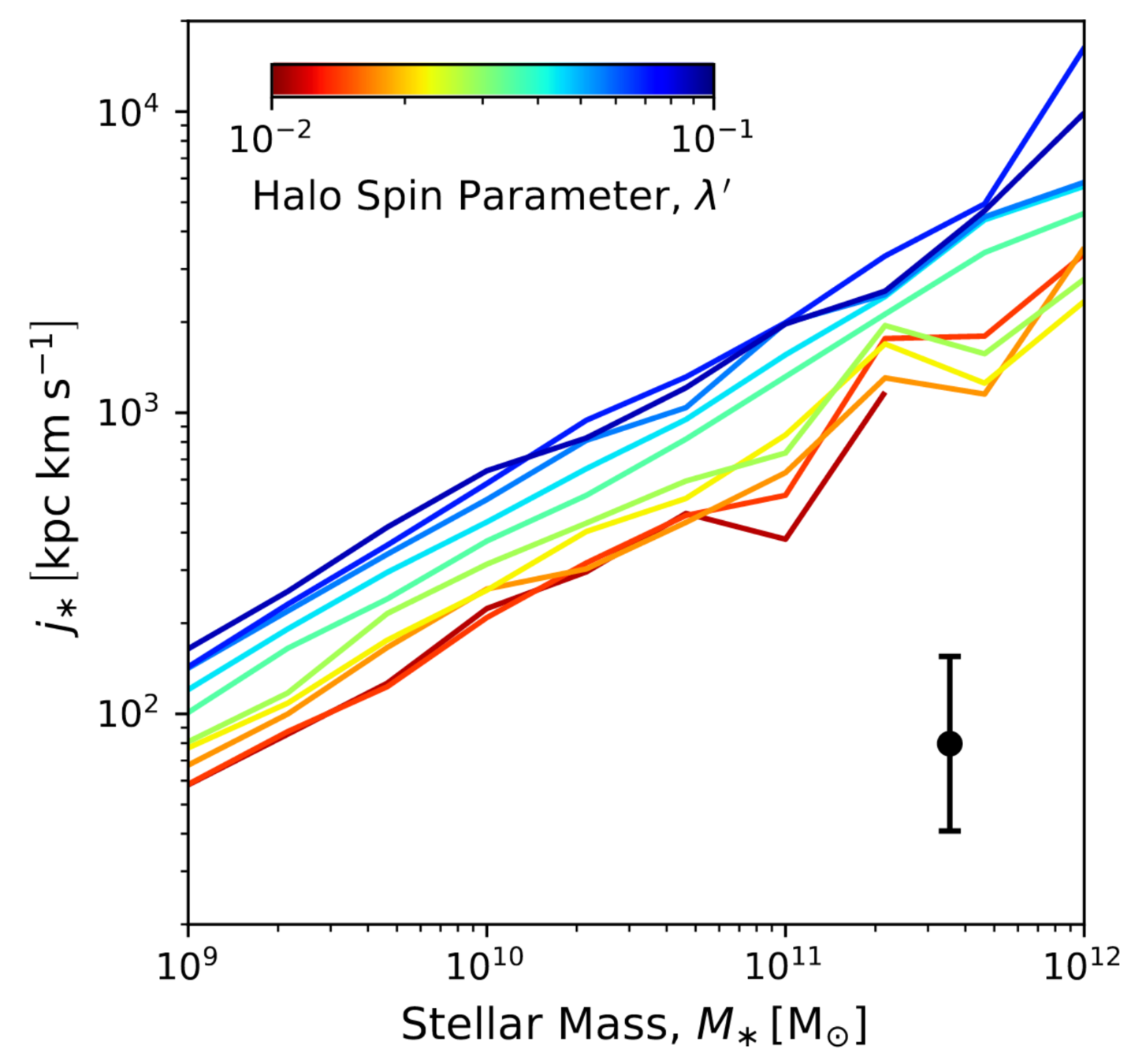
Halo and disk evolve separately,
but \(\lambda_\mathrm{baryon} \propto \lambda_\mathrm{DM}\)

Gas + stars spAM
Stars spAM
Halo spAM
Halo spAM
See Cadiou, Pontzen & Peiris+21
Corentin Cadiou

See Cadiou, Pontzen & Peiris+21
Special case: no massive satellite
Low tides
High tides
\(\mathcal{B}\searrow\)
\(R_\mathrm{eff} \nearrow \)
\(v/\sigma\nearrow\)
Corentin Cadiou
\(z=0\)
\( z = 100\)
[Genetic modifications: Roth+16, see also Rey&Pontzen 18, Stopyra+20]




Tide \(\nearrow\) delay merger
Tide \(\searrow\) hasten merger
Corentin Cadiou
This suggests a way to predict ab initio merger orbital parameters (e.g. spin)
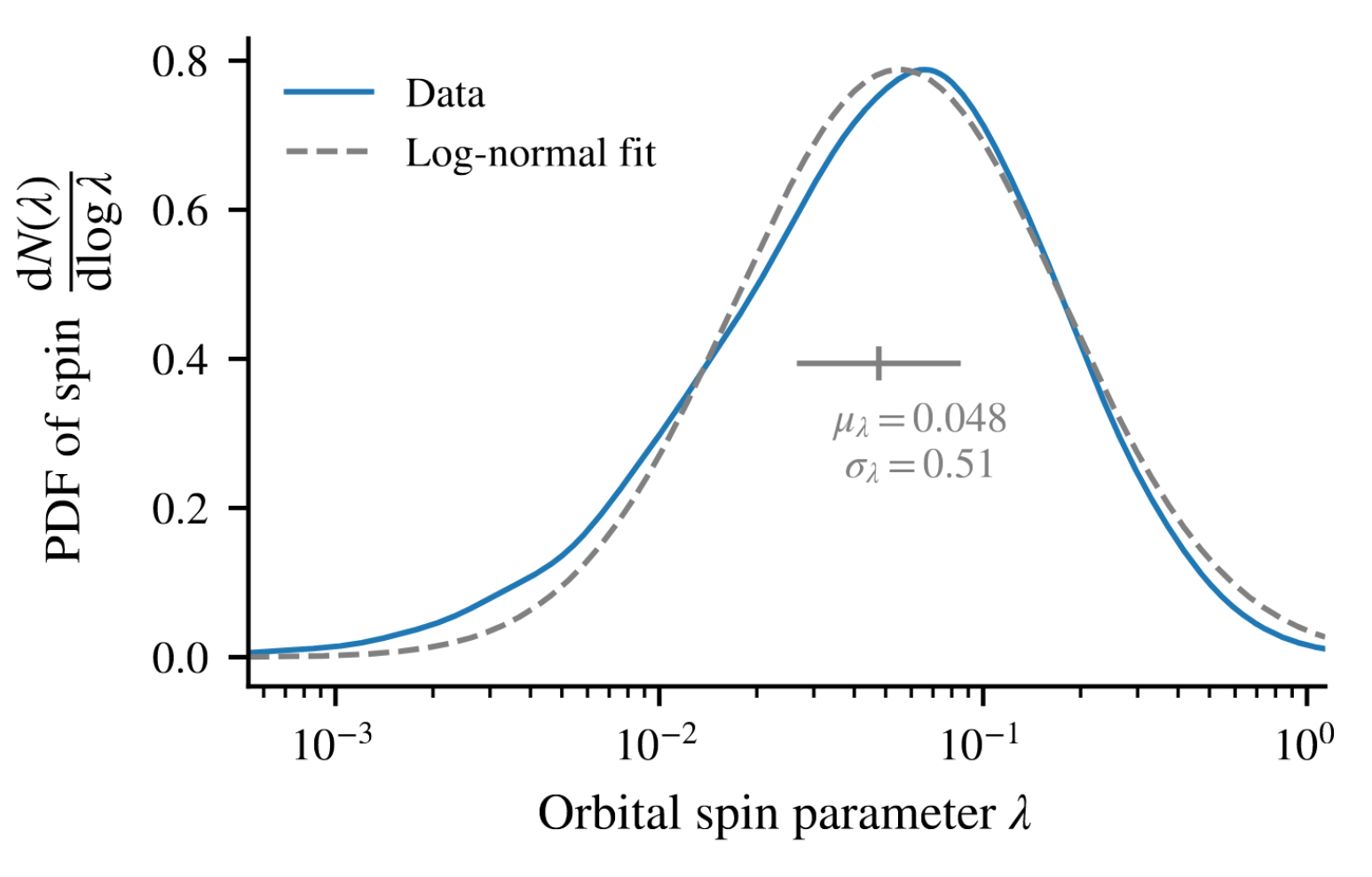
See Cadiou, Pichon-Pharabod+23




Corentin Cadiou
So far, I've shown effect of linear perturbations on galaxy formation.
How to probe non-linear couplings?
Corentin Cadiou



Corentin Cadiou


What if the galaxy had formed here instead?


Corentin Cadiou


What if the galaxy had formed here instead?


or here?
Corentin Cadiou

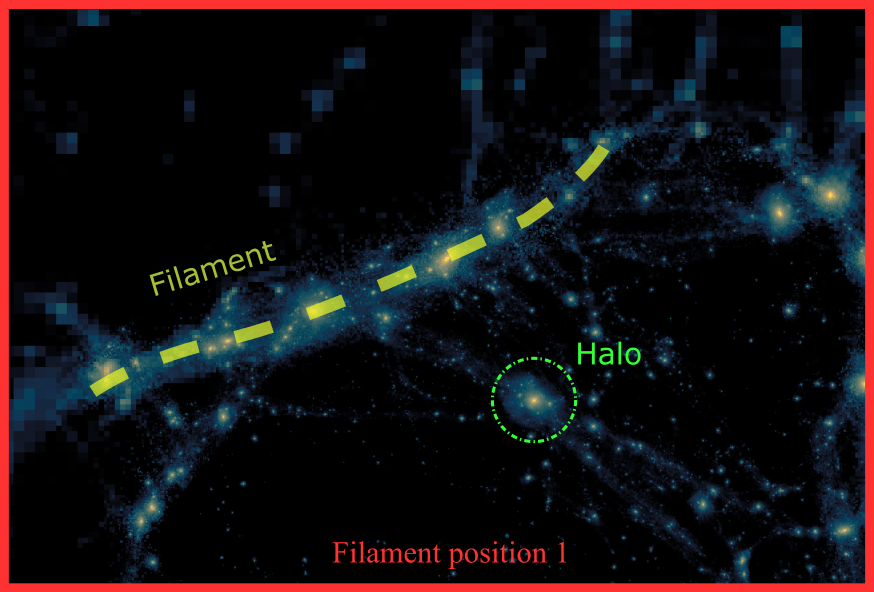
Splicing technique Cadiou, Pontzen & Peiris 21
Extended by A. Storck

Corentin Cadiou


Splicing technique Cadiou, Pontzen & Peiris 21
Extended by A. Storck


Corentin Cadiou



See Anatole Storck's poster for more information!
Far
Close
Halo (mis-)aligns itself to filament
Corentin Cadiou
Conclusions
Corentin Cadiou
-
Tides drive stellar angular momentum, which drives scaling relations
AM causes bulge to reduce, radius and \(v/\sigma\) to increase
Explains \(j_\star-M_\star-\mathcal{B}\) relation (and Tully-Fisher?)
-
\(j_\mathrm{gal}\) retain memory of the cosmic web
Galaxies are less stochastic than expected
Galactic spin & DM spins are partially independent at the level of individual galaxies
-
Non-linear effects are important to understand the origin of spin fully (so disk!)
At MW mass, the closer to a filament, the more \(\perp\) the halo spin
Galaxy simulations are in the pipes

Conclusions


Corentin Cadiou
What's the effect of anisotropic env DM/gal formation?
Study same object, different environment.
CC+21, arXiv: 2107.03407
Cosmic web drives AM acquisition... what scales? what's affected?
The “splicing” technique


- Generate ICs
- Integrate (\(N\)-nody)
- Select region of interest
- Trace back to ICs
- “Splice”
- Integrate again

\(t\)

Splicing: equivalent of constraining field at all points in spliced region
The causal origin of DM halo concentration


\(M^{(1)}_{200\mathrm{c}}, c^{(1)}_\mathrm{NFW}, \dots\)


\(M^{(2)}_{200\mathrm{c}}, c^{(2)}_\mathrm{NFW}, \dots\)


\(M^{(\dots)}_{200\mathrm{c}}, c^{(\dots)}_\mathrm{NFW}, \dots\)


\(M^{(10)}_{200\mathrm{c}}, c^{(10)}_\mathrm{NFW}, \dots\)
Same halo in 10× different environments
Repeat experiment for 7 halos (70 realisations in total)
Same halo in 10× different environments
Repeat experiment for 7 halos (70 realisations in total)


\(M^{(1)}_{200\mathrm{c}}, c^{(1)}_\mathrm{NFW}, \dots\)


\(M^{(2)}_{200\mathrm{c}}, c^{(2)}_\mathrm{NFW}, \dots\)


\(M^{(\dots)}_{200\mathrm{c}}, c^{(\dots)}_\mathrm{NFW}, \dots\)


\(M^{(10)}_{200\mathrm{c}}, c^{(10)}_\mathrm{NFW}, \dots\)

The causal origin of DM halo concentration
Same halo in 10× different environments
Repeat experiment for 7 halos (70 realisations in total)


\(M^{(1)}_{200\mathrm{c}}, c^{(1)}_\mathrm{NFW}, \dots\)


\(M^{(2)}_{200\mathrm{c}}, c^{(2)}_\mathrm{NFW}, \dots\)


\(M^{(\dots)}_{200\mathrm{c}}, c^{(\dots)}_\mathrm{NFW}, \dots\)


\(M^{(10)}_{200\mathrm{c}}, c^{(10)}_\mathrm{NFW}, \dots\)


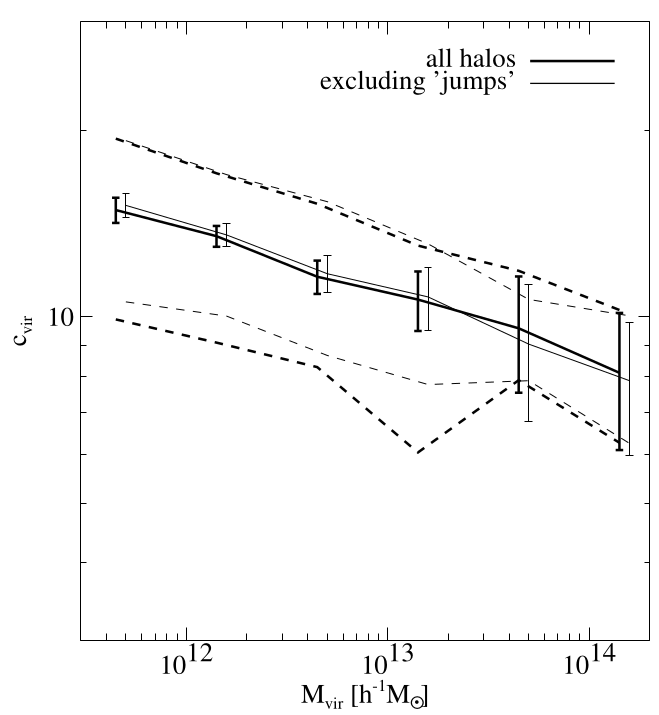
The causal origin of DM halo concentration
50% of population

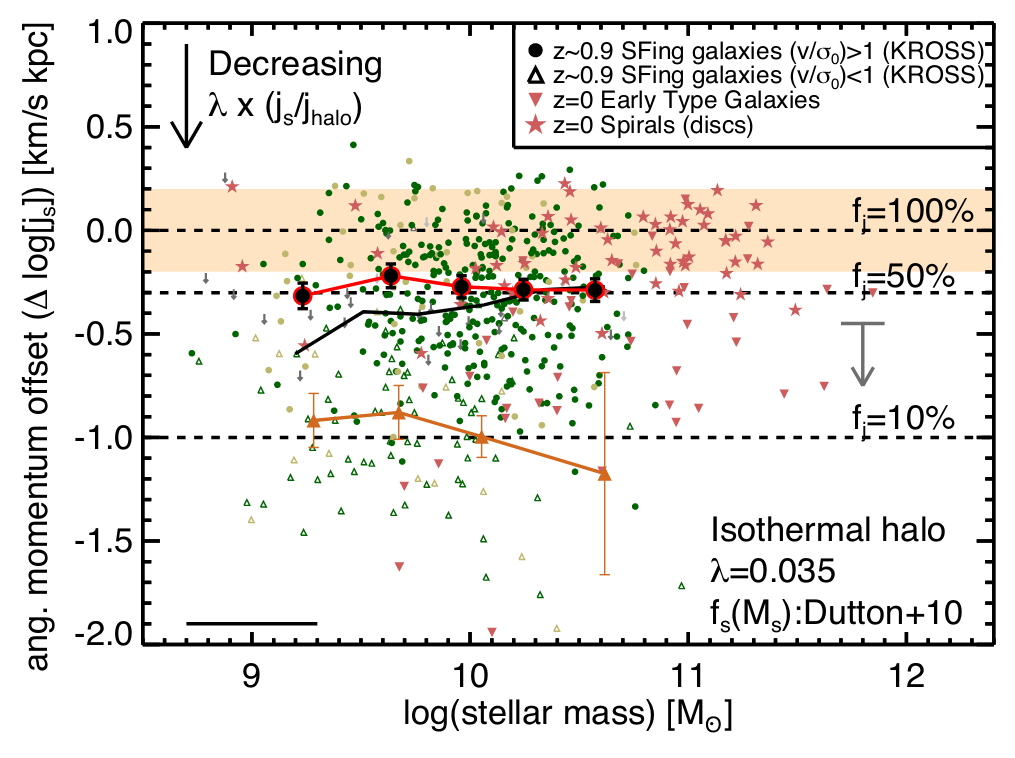
Harrison+17 (KMOS, \(z=1\))






Spiral galaxies \(\leftrightarrow\) high \(J_\star\)
What's the arrow of causality?
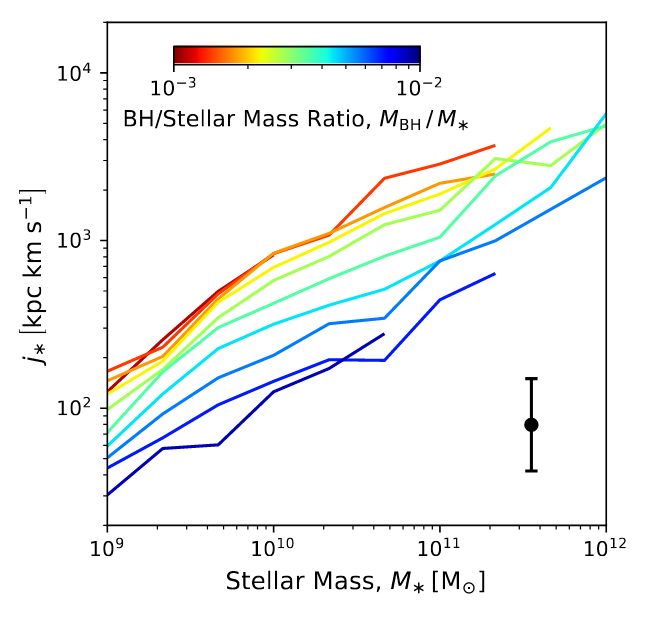
Rodriguez-Gomez+22 (TNG)


Angular momentum: controls disk formation?
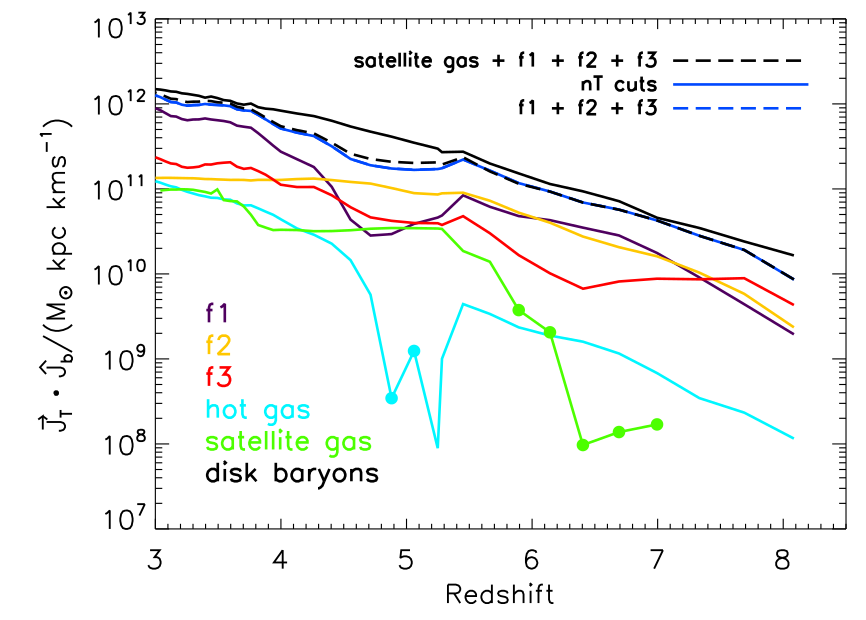
Tillson+15
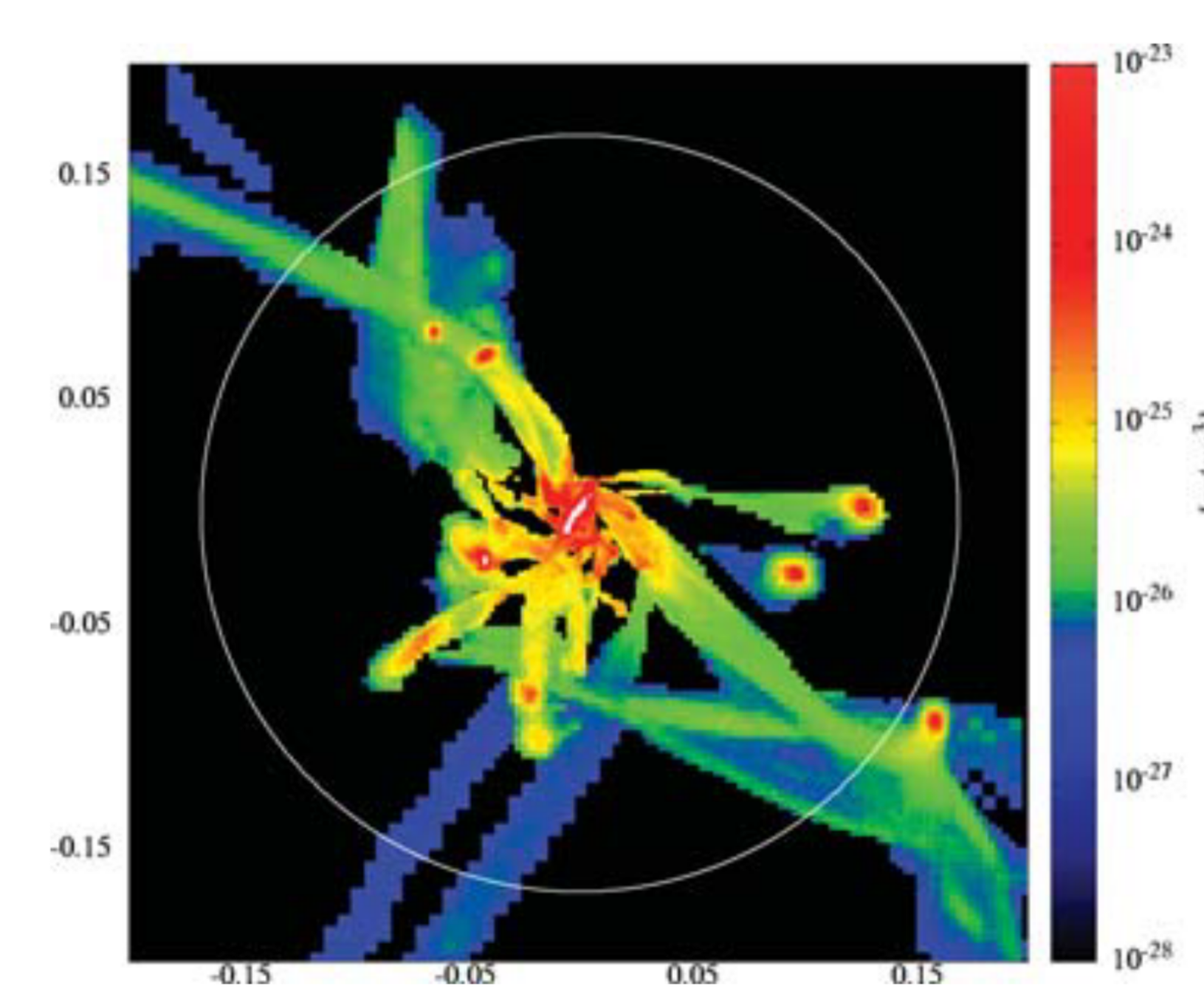
Dekel&Birnboim 06
High-z:
most of mass + AM flow along filaments
How do we study these effects?
Large volumes
sample \(p(M_\star, M_\mathrm{DM},\mathbf{J}, d_\mathrm{fil}, \dots)\)
This talk
sample \(p(\mathbf{J}|M_\star, M_\mathrm{DM}, d_\mathrm{fil}, \dots)\)
Angular momentum: bridging galaxy to cosmology
Lower-zs:
intrinsic alignment problem
Angular momentum: where are we?
Porciani+02
Rodriguez-Gomez+22
Predictions for \(j_\mathrm{DM}\) remain qualitative
\(j_\mathrm{DM}-j_\mathrm{\star}\)
weak correlation
(statistically strong)
- Is \(j_\mathrm{DM}\) chaotic or our theory poor?
- Do \(j_\mathrm{gal}\) retain memory of their environment?
-
How is AM transported to the disk?



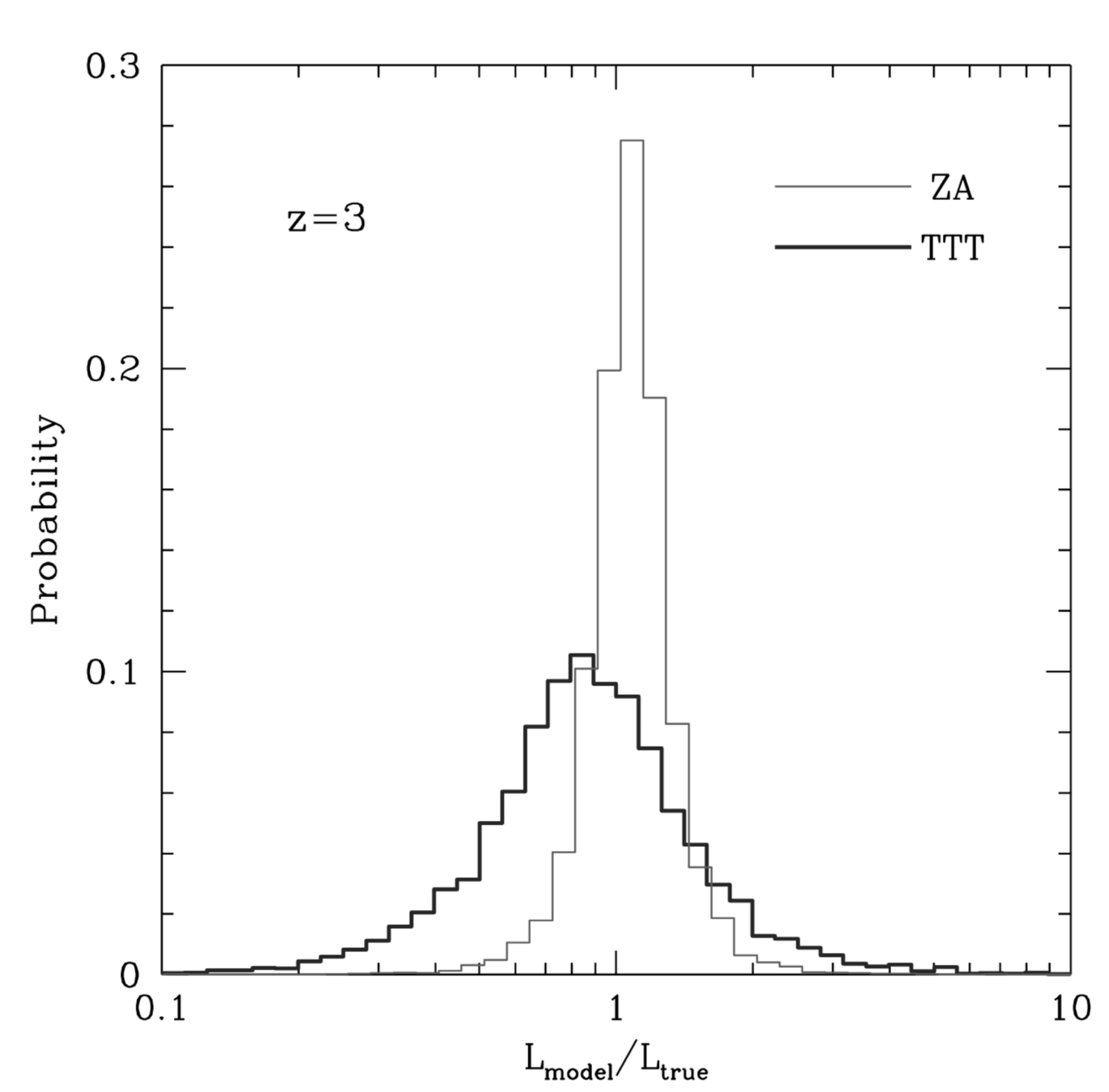
1. Is \(j_\mathrm{DM}\) chaotic or our theory poor?
First controlled experiment of testing tidal torque theory for individual halos
CC+21a, arXiv: 2012.02201
2. Do \(j_\mathrm{gal}\) retain memory
of the environment?
3. How is AM transported
to the disk?
Predicting angular momentum



\(z=0\)
\( z = 100\)
Predicting angular momentum



\(z=0\)
\( z = 100\)
[White 84]

Predicting angular momentum



\(z=0\)
\( z = 100\)
[Genetic modifications: Roth+16, see also Rey&Pontzen 18, Stopyra+20]



Predicting angular momentum










Time
Sampling \(p(\mathbf{J}|M_\mathrm{DM}, d_\mathrm{fil}, \dots)\)
Predicting angular momentum


Time








Predicting angular momentum



✅ AM of fixed DM regions responds ~linearly (so is not chaotic!)
Improve theory?
- Go to non-linear order (non-linear TTT)
- Accurate prediction of Lagrangian patch boundaries (see Musso&Sheth 23)
1. Is \(j_\mathrm{DM}\) chaotic or our theory poor?
2. Do \(j_\mathrm{gal}\) retain memory
of the environment?
First controlled experiment of angular momentum accretion on individual galaxies
CC+22, arXiv: 2206.11913
Main idea: stars are deeper in potential well so less sensitive to what happens at large scales
⇒ stellar Lagrangian patch should be more stable to perturbations
3. How is AM transported
to the disk?
1. Is \(j_\mathrm{DM}\) chaotic or our theory poor?
2. Do \(j_\mathrm{gal}\) retain memory
of the environment?
3. How is AM transported
to the disk?
CC+Pichon+Dubois, 21, arXiv: 2110.05384
Kocjan, CC in prep.
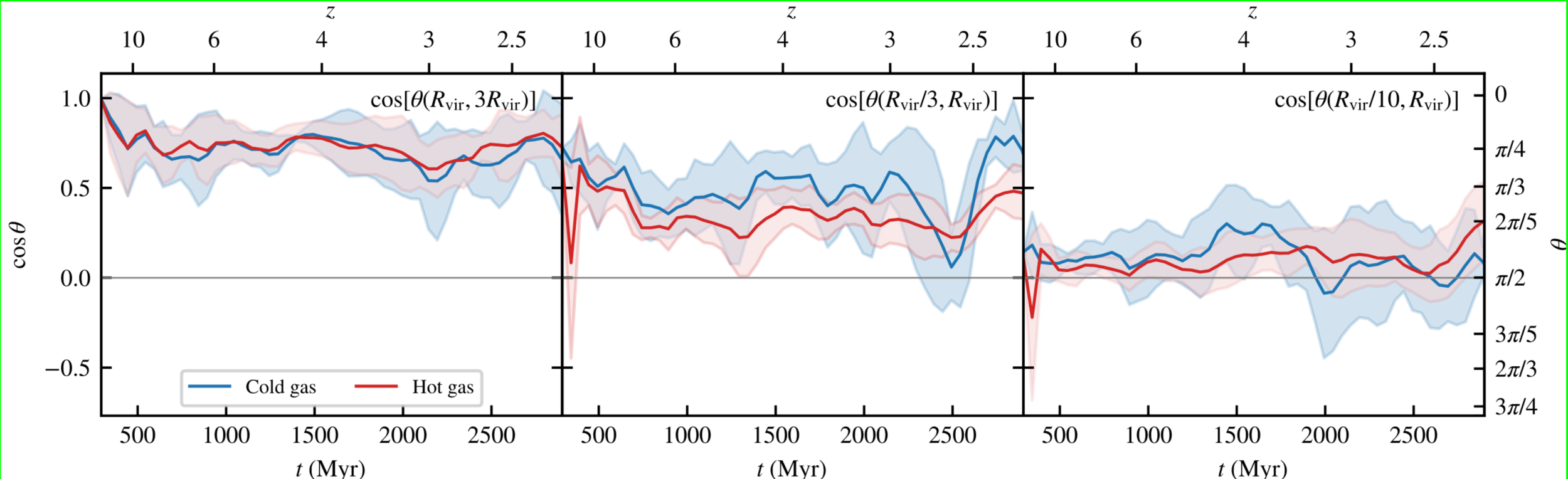
Dynamics of angular momentum
Realignment between…
…\(3R_\mathrm{vir}\) and \(R_\mathrm{vir}\)
…\(R_\mathrm{vir}\) and \(R_\mathrm{vir}/3\)
…\(R_\mathrm{vir}\) and \(R_\mathrm{vir}/10\)
✅ Most of realignment happens in “CGM” (\(\leq R_\mathrm{vir}/3\))
Mostly due to grav. torques (consistent with e.g. Danovich+15)
[CC+21]
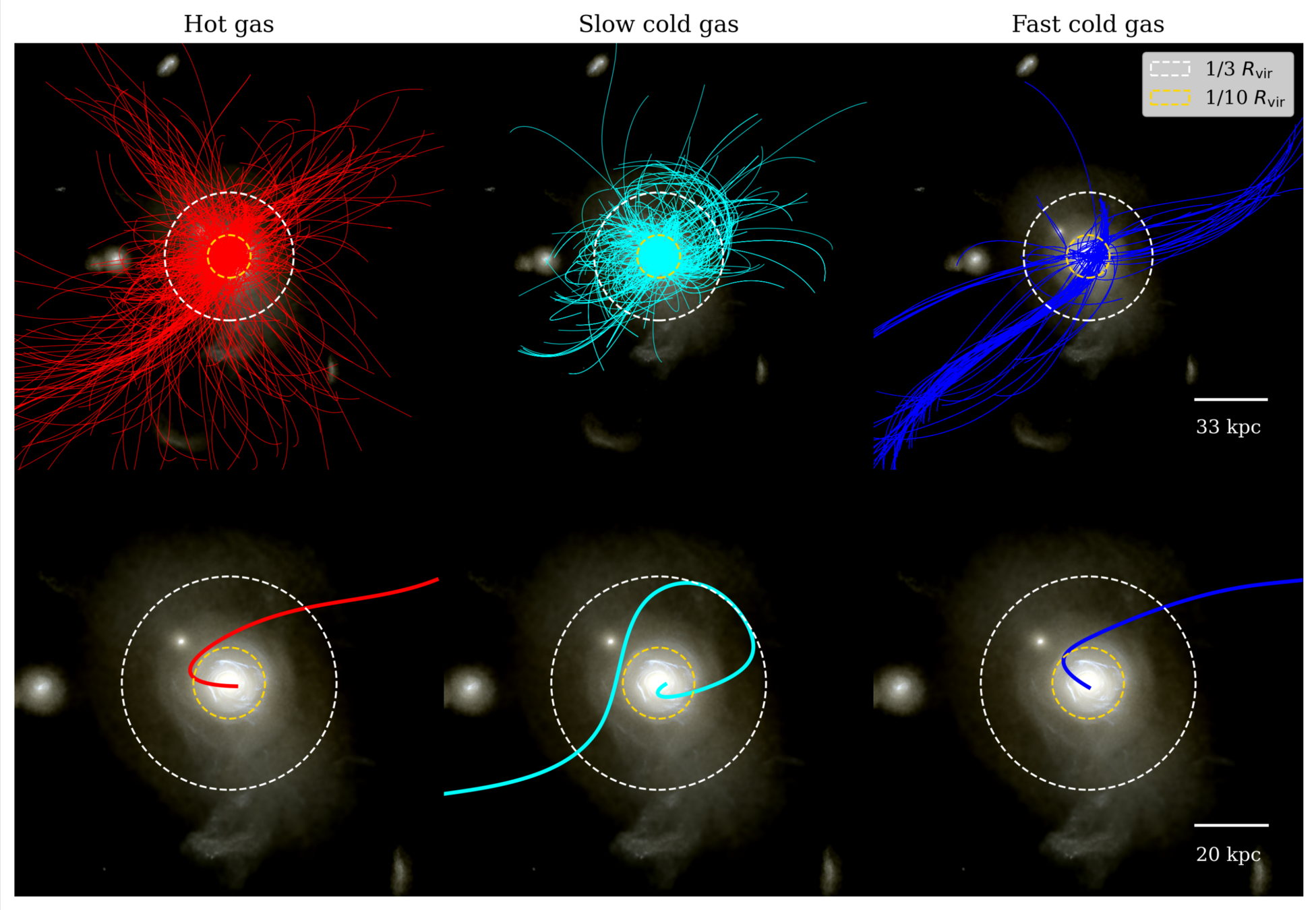
\(t_{1/3}\)
\(t_{\star}\)
\(T_\mathrm{max}\) between \(2 R_\mathrm{vir}\) and \(R_\mathrm{vir}/3\)?
\(\leq 3\times10^4\,\mathrm{K}\)
Cold accretion
\(\geq 5\times10^5\,\mathrm{K}\)
Hot accretion
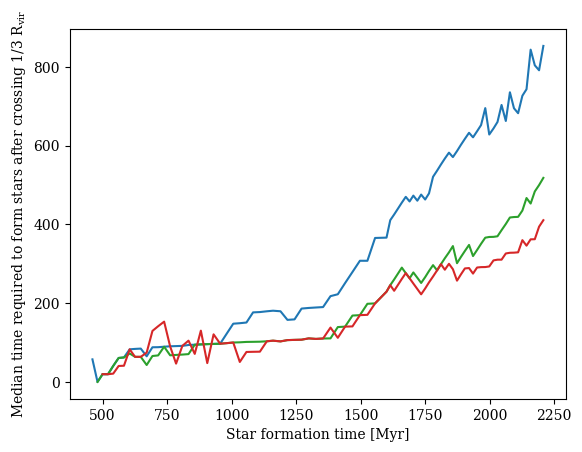
[Kocjan, CC+ in prep]
What happens in the CGM?



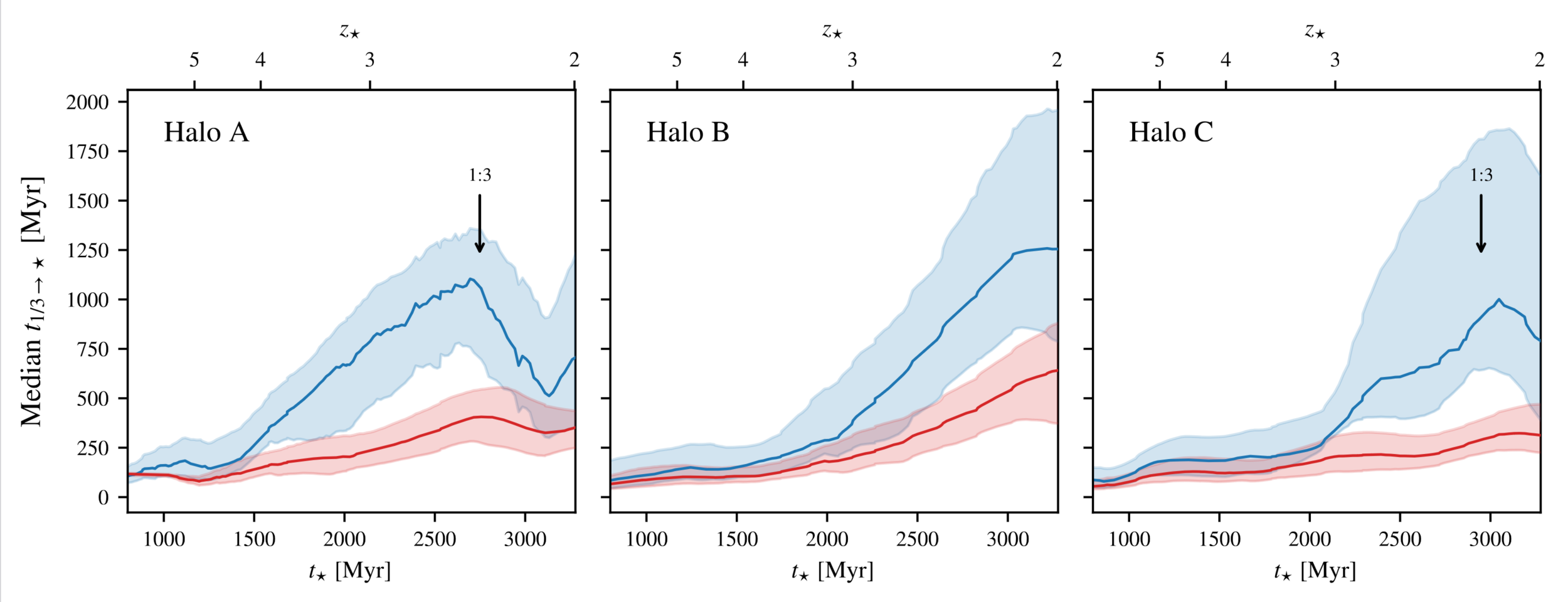

✅ Cold accretion is slow to form stars
Quick depletion right after merger
[Kocjan, CC+ in prep]
The effects of environment on halo properties
Kraljic+18 [see also Laigle15, Song+21,…]
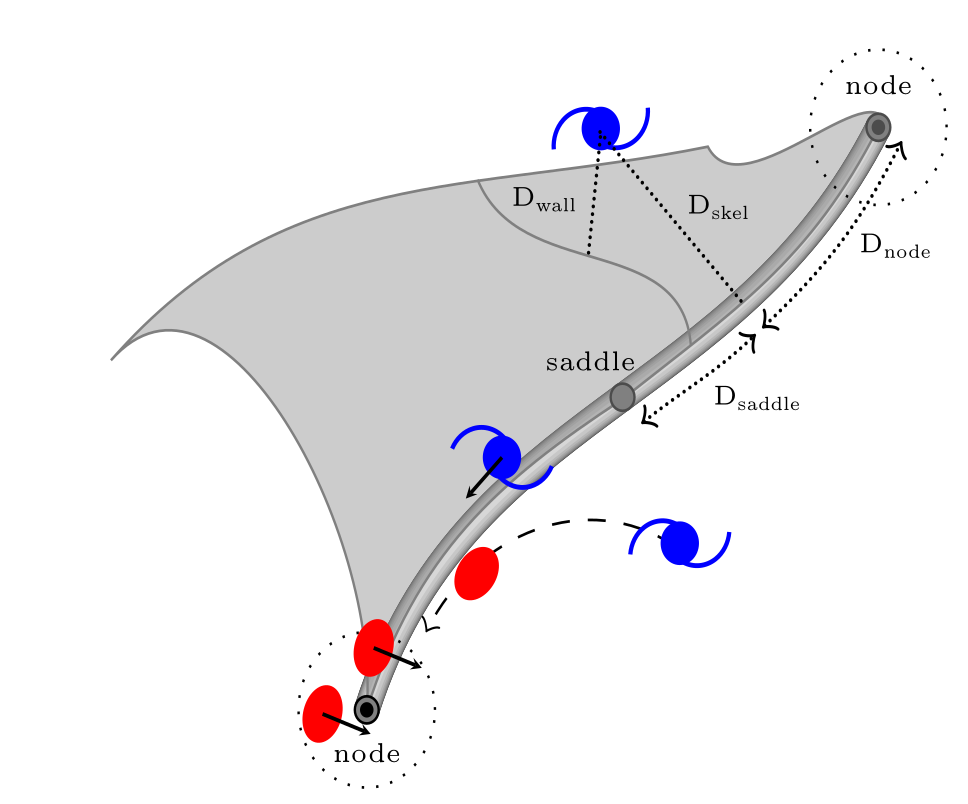



- \( M_\mathrm{DM}(\text{node}) \) > \(M_\mathrm{DM}(\text{fil}) \) >\(M_\mathrm{DM}(\text{void})\), higher clustering
- spins align with cosmic web ⇒ issue for weak lensing
- \(v/\sigma(\mathrm{fil})>v/\sigma(\mathrm{void})\) ⇒ bias in galaxy formation
- ….
The effects of environment on halo properties




Isotropic effects
Kaiser bias, cluster vs. groups, ...
From theory: \(M\propto \int\mathrm{d}^3R\rho\)
Mass regulated
An-isotropic effects
Intrinsic alignment, formation of disks?
From theory: \(J \propto \int\mathrm{d}^3R \nabla \phi\)
Angular momentum regulated?
Predicting angular momentum



\(z=0\)
\( z = 100\)
\[\mathbf{L}_\mathrm{lin.} \propto \int\mathrm{d}^3q(\mathbf{q}-\bar{\mathbf{q}})\times \nabla\phi\]
Position w.r.t. center
Velocity
[White 84]

Note: vanishes at 1st order in a sphere
\[ \int_\Gamma \mathrm{d}^3{q}(\mathbf{q}-\mathbf{\bar{q}}) \times\nabla\phi = \int_{\partial\Gamma}\phi(q)(\mathbf{q}-\mathbf{\bar{q}})\times\mathrm{d}\mathbf{S}\]
Note: the following is a (poor) approximation:
\[ \mathbf{L} \propto \epsilon_{ijk} T_{jl}I_{lk},\quad\text{with \textbf{T} the tidal tensor and \textbf{I} the inertia tensor}\]

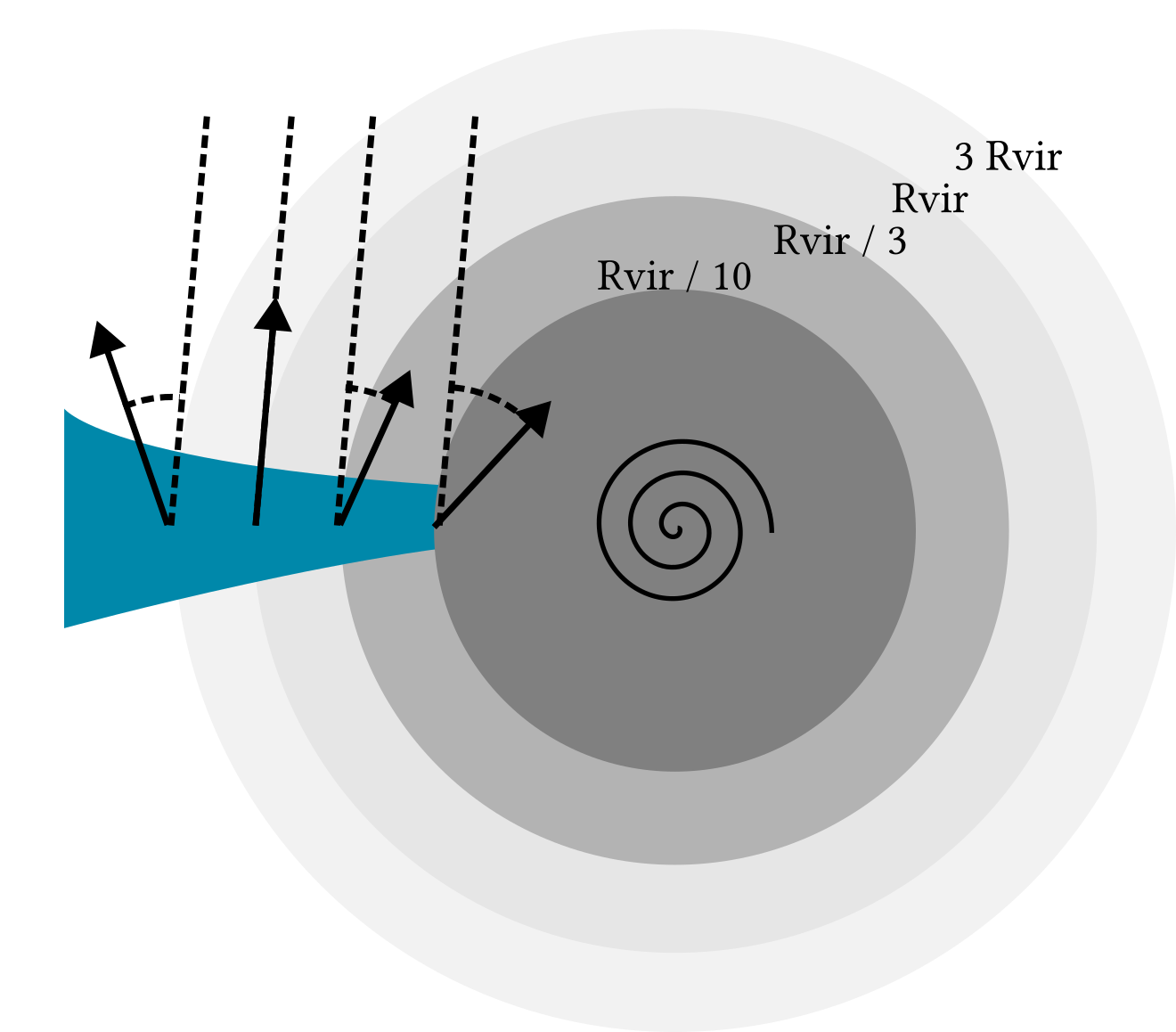
[See also Danovich+15, Prieto+17]


✅ Most of re-alignment happens in the CGM \(0.1\leq \displaystyle\frac{r}{R_\mathrm{vir}}\leq 0.3\)
The longer gas remains in CGM, the more it realigns with disk
[See also Danovich+15, Prieto+17]

Ongoing work by Z. Kocjan

[Kocjan, CC+ in prep]
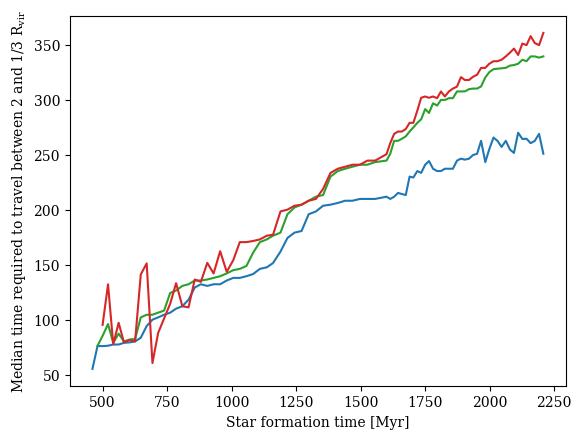
Filamentary accretion ~ Cold flow = \(T \leq 10^5\mathrm{K}\) for \(0.3R_\mathrm{vir} < r < 2R_\mathrm{vir}\)


Filamentary accretion ~ Cold flow = \(T \leq 10^5\mathrm{K}\) for \(0.3R_\mathrm{vir} < r < 2R_\mathrm{vir}\)
Not necessarily fast-track to star formation ⇒ lose connection to CW?
[Kocjan, CC+ in prep]
\(M_\mathrm{DM}(z=2)\approx 10^{11}-10^{12} \mathrm{M_\odot}\)

Ongoing work by Z. Kocjan
Ex Uno Plures: direct measure of the impact of the cosmic web on individual objects to shed light on their population statistics



Corentin Cadiou
The Co-evolution of the CW and Galaxies across Cosmic Time

The causal origin of DM halo concentration


$$\rho_\mathrm{DM}(r) = \frac{\rho_0}{\frac{r}{R_\mathrm{vir}/c} \left(1 + \frac{r}{R_\mathrm{vir}/c}\right)^2}$$
Wechsler+02
Origin of scatter at fixed \(M_\mathrm{vir}\)?
Predicting angular momentum



- Angular momentum of individual regions can be predicted accurately.
- AM of halos ⇒ requires boundaries of patch


\[\mathbf{L}_\mathrm{lin.} \propto \int\mathrm{d}^3q(\mathbf{q}-\bar{\mathbf{q}})\times \nabla\phi\]
[On patch boundaries: see Lucie-Smith+18]
Splicing in 1D





Splicing in 1D


Most likely* field \(f\) with
- same value in spliced region (\(a\)),
- as close as possible outside (\(b\))



Mathematically \(f\) is solution of:
\( f= a\) in \(\Gamma\)
minimizes \(\mathcal{Q} = (b-f)^\dagger\mathbf{C}^{-1}(b-f) \) outside \(\Gamma\)
Can we control baryonic
angular momentum?
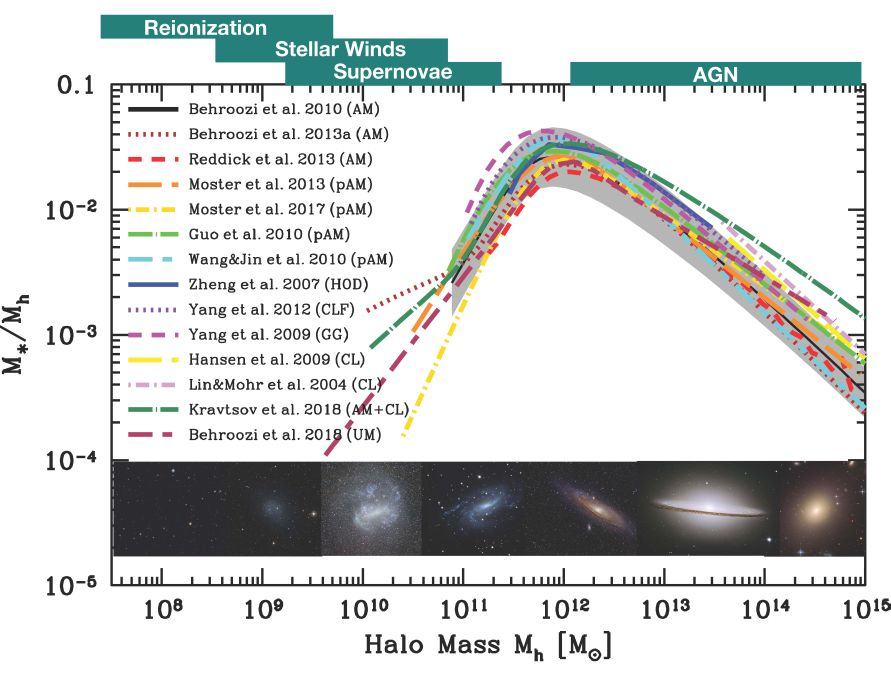
Wechsler & Tinker 18
\({\color{red}M_\star} / M_\mathrm{h} \ll \Omega_b / \Omega_m \)
⇒ baryons & DM stem from different regions


Baryons more strongly bound
⇒ less prone to being ejected



Verify that
\[\xi_\mathrm{lin}(r) \sim \left\langle {\color{green}\underbrace{\delta(x=d)}_\mathrm{in}} {\color{purple} \underbrace{\delta(x=d+r)}_\mathrm{out}}\right\rangle \]
is the same in spliced / ref simulation.

Verify that
\[\xi_\mathrm{lin}(r) \sim \left\langle {\color{green}\underbrace{\delta(x=d)}_\mathrm{in}} {\color{purple} \underbrace{\delta(x=d+r)}_\mathrm{out}}\right\rangle \]
is the same in spliced / ref simulation.

Verify that
\[\xi_\mathrm{lin}(r) \sim \left\langle {\color{green}\underbrace{\delta(x=d)}_\mathrm{in}} {\color{purple} \underbrace{\delta(x=d+r)}_\mathrm{out}}\right\rangle \]
is the same in spliced / ref simulation.

Temporary conclusions
-
angular momentum is predictable
-
boundary of halos in the ICs is a hard problem
⇒ limits practicality of predictions (for now)
-
baryons appear to be simpler!
⇒ good news for weak lensing predictions
⇒ key to understand morphology


Galaxy formation in cosmology: the role of the environment




Environmental effects:
- source of “pollution” in weak lensing surveys
⇒ intrinsic alignment
- extra parameters in semi-analytical models
⇒ galaxy-halo correlation




+

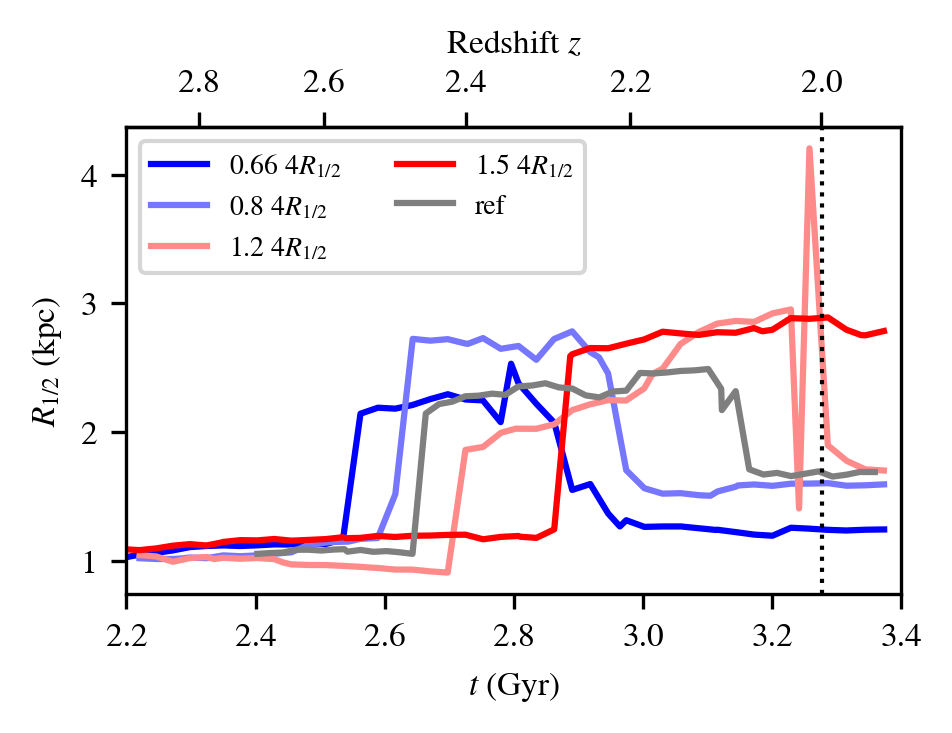
\( R_{1/2} \)
\( l_0 \times 1.2\)
\( l_0 \times 1.5\)

\( l_0 \times 0.66\)
\( l_0 \times 0.8\)

\( l_0 \times 0.66\)
\( l_0 \times 0.8\)
\( l_0 \times 1.2\)
\( l_0 \times 1.5\)


\( l_0 \times 1.2\)
\( l_0 \times 1.5\)

\( l_0 \times 0.66\)
\( l_0 \times 0.8\)



\( l_0 \times 1.2\)
\( l_0 \times 1.5\)

\( l_0 \times 0.66\)
\( l_0 \times 0.8\)



- AM of baryons originates from initial conditions…
- can be controlled…
- and regulate galaxy morphology
- Negligible AGN/SN global self-regulation
Galaxy formation
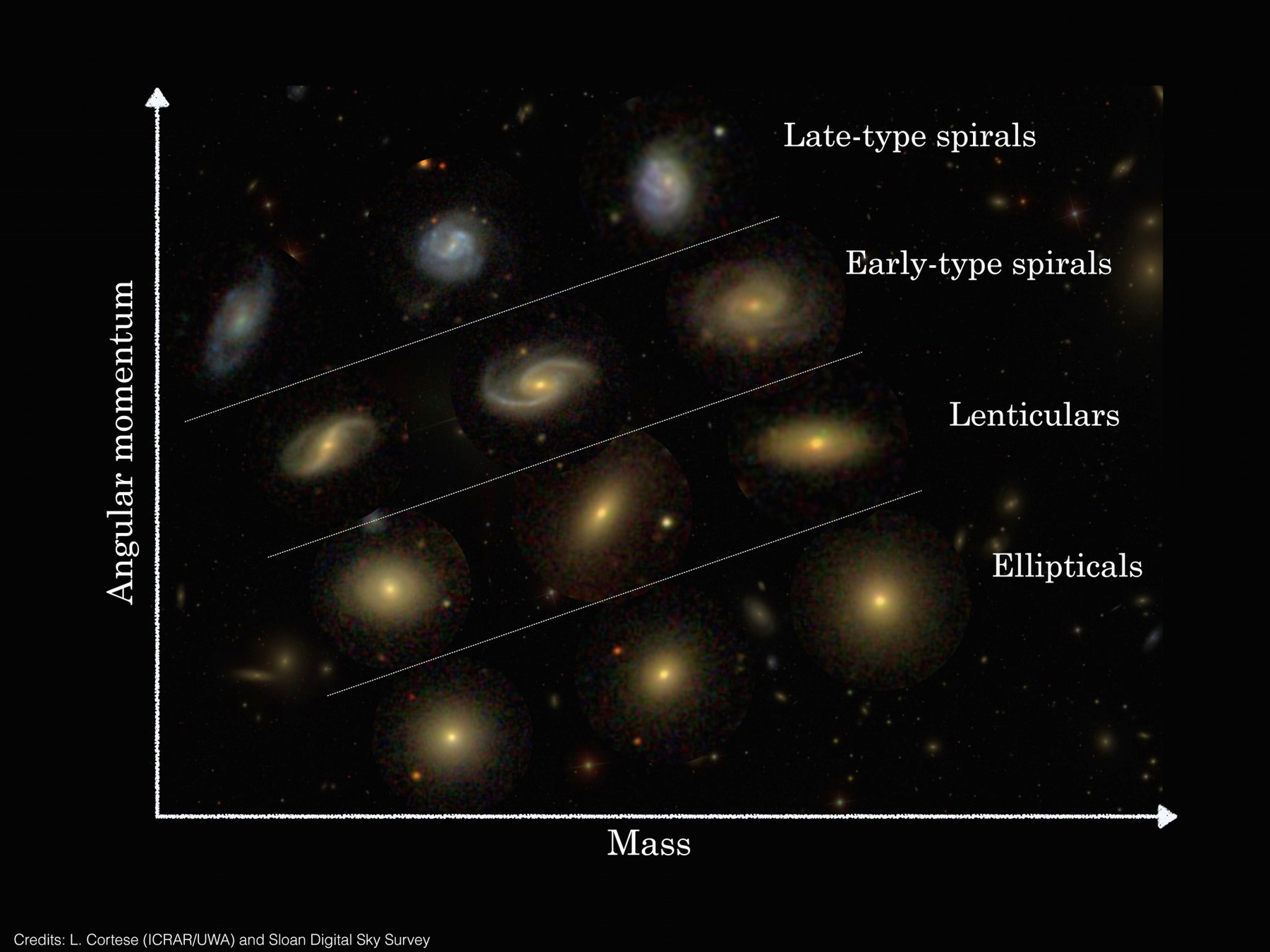
[L. Cortese; SDSS.]



[Dubois+16]
AGN no AGN
Origin of morphological diversity at fixed mass?

[L. Cortese; SDSS.]



[Dubois+16]
AGN no AGN
Origin of morphological diversity at fixed mass?
How to explain environmental effects?

[Kraljic+ in prep]

Galaxy formation

[Danovich+15]
The origin of high \(z\) angular momentum

[Danovich+15]
I. Torque with cosmic web
The origin of high \(z\) angular momentum

[Danovich+15]
I. Torque with cosmic web
II. Transport at constant AM
The origin of high \(z\) angular momentum

[Danovich+15]
I. Torque with cosmic web
II. Transport at constant AM
III. Torque down in inner halo
The origin of high \(z\) angular momentum

[Danovich+15]
I. Torque with cosmic web
II. Transport at constant AM
III. Torque down in inner halo
IV. Mixing in inner disk & bulge
The origin of high \(z\) angular momentum
The origin of high \(z\) angular momentum

[Danovich+15]
IV. Mixing in inner disk & bulge
Fraction that ends up in disk vs. IGM?
Influence of galactic physics?
III. Torque down in inner halo
Origin of torque down (pressure or gravity)?
Loss of link with cosmic AM?
II. Transport at constant AM
Same evolution in cold/hot accretion modes?
I. Torque with cosmic web
Predict pre-accretion AM?
Alignment with environment?
The origin of high \(z\) angular momentum

[Danovich+15]
IV. Mixing in inner disk & bulge
Fraction that ends up in disk vs. IGM?
Influence of galactic physics?
III. Torque down in inner halo
Origin of torque down (pressure or gravity)?
Loss of link with cosmic AM?
See Cadiou+21c
II. Transport at constant AM
Same evolution in cold/hot accretion modes?
I. Torque with cosmic web
Predict pre-accretion AM?
Alignment with environment?
The origin of high \(z\) angular momentum

[Danovich+15]
IV. Mixing in inner disk & bulge
Fraction that ends up in disk vs. IGM?
Influence of galactic physics?
III. Torque down in inner halo
Origin of torque down (pressure or gravity)?
Loss of link with cosmic AM?
II. Transport at constant AM
Same evolution in cold/hot accretion modes?
I. Torque with cosmic web
Predict pre-accretion AM?
Alignment with environment?
On the causal origin of dark matter halo and galaxy angular momentum: replacing galaxies in their cosmological context | IAP Symposium 2023
By Corentin Cadiou
On the causal origin of dark matter halo and galaxy angular momentum: replacing galaxies in their cosmological context | IAP Symposium 2023
Presentation at IAP symposium
- 438



