Graphics Programming Virtual Meetup


Discord
Homogeneous Perspective Transform
Jim Blinn's Corner
May 1993
Link
Perspective Transformation Matrix
- Transforms camera space to 'screen space'
- Makes 3d scenes look like they do in real life
- A non-affine transformation
- Is harder to intuit than affine transformations
Affine?
- Affine transformations preserve the following:
- Collinearity
- Point on a line still line on a line after transformation
- Ratios of distances
- midpoint of a line segment is the same after transformation
- Collinearity
- Translation, Rotation, Scaling, and Shear are all Affine
- Affine 4x4 matrices have `(0,0,0,1)` in the last column
Non-Affine
- A superset of affine transformations
- Do not preserve ratios of distances
- Midpoint moves around
- Commonly called 'Projection Transformations'
- Perspective transformation falls in this category
- Non-Affine 4x4 matrices do not have `(0,0,0,1)` in the last column.
- These values represent the projection component of the matrix
Homogeneous Coordinates
Wikipedia says:
"Any point in the projective plane is represented by a triple (X, Y, Z), called homogeneous coordinates or projective coordinates of the point, where X, Y and Z are not all 0. The point represented by a given set of homogeneous coordinates is unchanged if the coordinates are multiplied by a common factor. "
Homogeneous Coordinates
- The coordinate system used in projective geometry
- For 3d Cartesian coordinates, tack on a w coordinate
- Converting between Cartesian requires dividing the x, y, and z by the w coordinate
- (X, Y, Z) == (x/w, y/w, z/w)
- Can represent points at infinity
- (x, y, z, 0) - the 0 for the w value is used to denote ∞
- For every (X, Y, Z) Cartesian coordinate, there are infinite homogeneous coordinates
- As w divides x,y,z into X, Y, Z, this w could scale arbitrarily
Fun things with these coordinates
- Being able to represent ∞ means meaningful geometric calculations can happen
- A negative w wraps the x,y,z around infinity
- (1, 0, 0, w) with [w = -0.1] is (-10, 0, 0)
- Also: (-1, 0, 0, 0) & (1, 0, 0, 0) are the same point
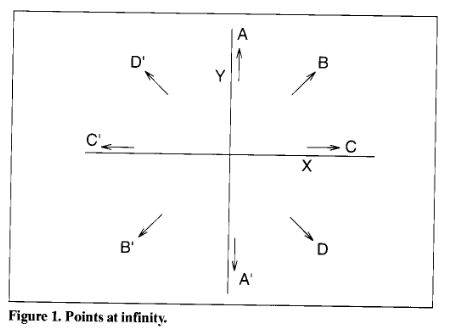
- Creates a sort of mobius twist to the geometry
4 "coordinate" spaces
- 3D - Cartesian before perspective transformation
- (X, Y, Z)
- 3DH - Homogeneous before perspective transformation
- (x, y, z, 1) - x,y,z have same value as X, Y, Z
- here things lie in the w=1 hyperplane in 4D space
- 3DHP - Homogeneous after perspective transformation -
- (x, y, z, w) - different values than before
- 3DP - Cartesian after perspective transformation
- (X, Y, Z) - (x/w, y/w, z/w) - divide by w
Simple Perspective
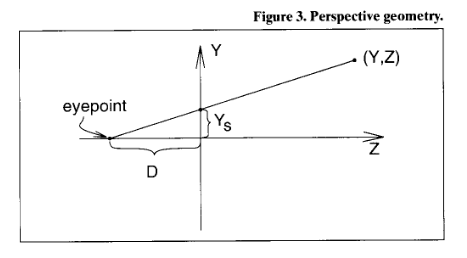
\frac{Y_s}{D} = \frac{Y}{Z + D}
\\
Y_s = \frac{Y}{Z/D + 1}
\\
\frac{Y}{Z/D + 1} = \frac{y_s}{w_s}
\\
w_s = Z/D + 1
(x_s, y_s, z_s, w_s) = (X, Y, Z, Z/D + 1)
Simple Perspective as a Matrix
- Note: Row order
(x_s, y_s, z_s, w_s) =
(X, Y, Z, 1)
\begin{bmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 1/D\\
0 & 0 & 0 & 1\\
\end{bmatrix}
= (X, Y, Z, 1) \textbf{P}
- The matrix multiplication is in homogeneous space
- To get real world values, divide by the resulting W expression, 1/D + 1 ( I think this is the expression)
Z coordinate transformation
- Follows the equation
- Z_s = Z / ( Z/D + 1)
- (X, Y, 0, 1)P = (X, Y, 0, 1)
- z = 0 plane doesn't move
- (0, 0, -D, 1)P = (0, 0, -D, 0)
- Eyepoint moves to infinity
- (0, 0, D, 0)P = (0, 0, D, 1)
- A point infinitely away becomes a local point
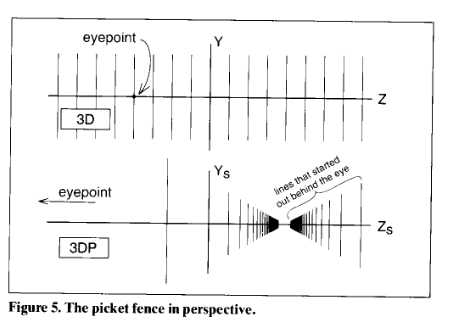
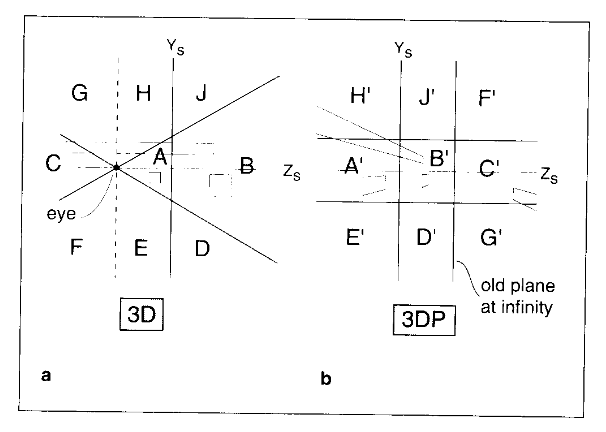
Homogeneous Space Interpretation
- Perspective transform is a shear in the w direction
- Points on 3DP have w=1
- These points shear up and down to get 3DHP
- Then they project back onto w=1 for 3DP
- note how the Z=0 and Z=∞ move
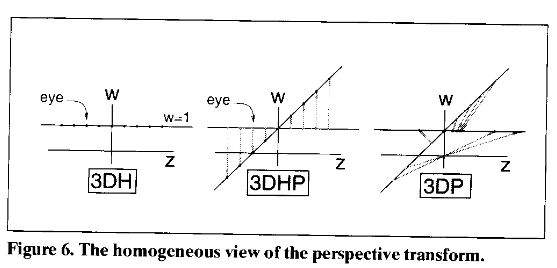
And now in stereo!
- The projection moves the points in the W axis
- But not the X or Z
- Converting back to Cartesian coordinates yields our perspective transformation
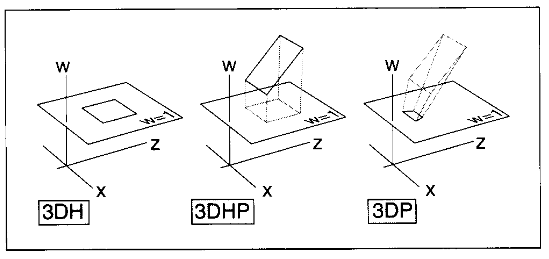
A view from the real world
- Elides the intermediate, 4 dimensional steps
- Good visualization of the final output
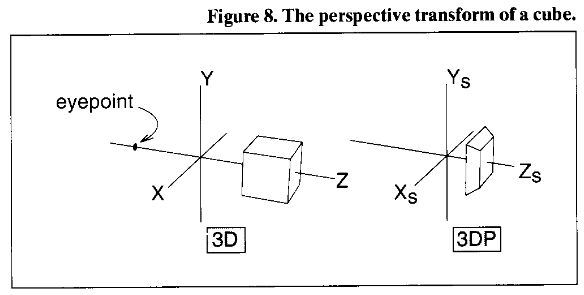
Perspective Projection is a 3D transformation
- The previous slides Cube is now deformed
- But its not 'on' a flat plane
- This is handled by the rasterizer. It can now use the `X, Y` coordinate and simply scale + translate to go from NDC to framebuffer coordinates.
- In a sense its doing a 'orthogonal projection' because depth doesn't alter the shape in that final process
Note about GPU pipelines
- Post-vertex, the pipeline will divide by w
- Vertex positions shouldn't have w = 0
- Normals and other attributes dont get divided
- Also fixed function vs programmable GPU's altered the pipeline
- The math however stays the same
Ultimate Understanding
YZ slice of space. Y=0 doesn't move
Little details that add a lot of noise to the matrix
- The core of the perspective is the homogeneous transformation & back again
- Deciding how the near & far, left & right, top & bottom planes depend on the set of conventions used
- Whether depth is [-1, 1] or [0,1]
- Generally the X and Y axis are [-1, 1]
"Fuller" Perspective Matrix
- Use the 'field of view' for width & height
- Zn & Zf are the near and far clipping planes
- (again, row-column)
\begin{bmatrix}
c & 0 & 0 & 0\\
0 & c & 0 & 0\\
0 & 0 & Q & s\\
0 & 0 & -QZ_n & 0\\
\end{bmatrix}
\\
s = sin(fov/2)\\
c = cos(fov/2)\\
Q = -\frac{s}{1-Z_n/Z_f}
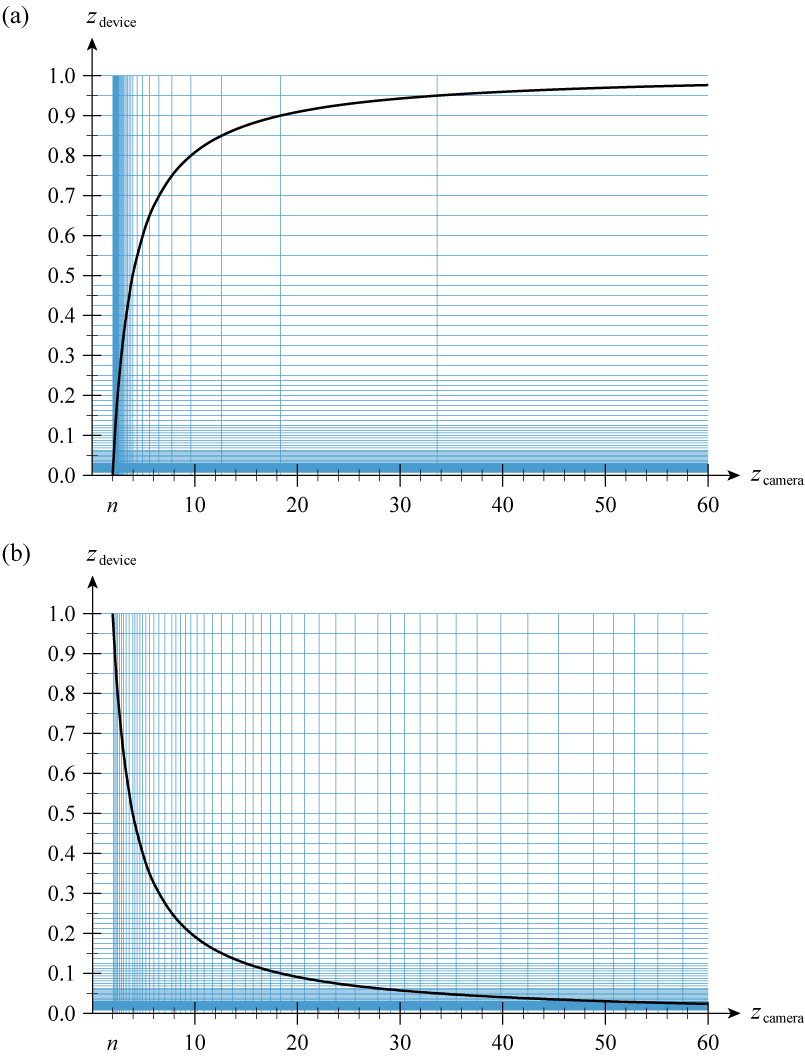
Reverse-Z, a better solution to depth
- This paper describes needing to carefully select the near and far planes
- Flipping the table on the problem by reversing which direction we store Z values fixes this
- I can confirm it is awesome
- Deserves its own talk...
Graphics Programming Virtual Meetup
The Homogeneous Perspective Transform
By Charles Giessen
The Homogeneous Perspective Transform
- 168


